不平衡非線性負載下三相逆變器的建模與控制

馬 皓 林 釗 王小瑞

?

不平衡非線性負載下三相逆變器的建模與控制

馬 皓 林 釗 王小瑞

（浙江大學電氣工程學院 杭州 310027）

為緩解實際應用場合中不平衡非線性負載對三相逆變器輸出電壓的影響，并改善混合負載切換時的動態特性，本文提出了基于廣義狀態空間平均的建模方法和電感電流滑動平均的控制策略。通過廣義狀態空間平均法對平衡負載下的逆變器進行了準確的建模，并在dq0坐標系下設計了PI控制器，最后利用電感電流滑動平均方法使PI控制器適于三相不平衡負載和非線性負載。與傳統控制方法的對比實驗表明，本文提出的模型和控制策略能夠在保證混合負載下三相電壓平衡的基礎上，較好地提高負載切換時的動態特性。

不平衡非線性負載 三相三線制逆變器 廣義狀態空間平均法 dq0變換 電感電流滑動平均

0 引言

分布式發電的迅猛發展使微電網的應用越來越廣泛。微電網中的負載大部分都含有不平衡或非線性的成分。不平衡的三相線性負載將給逆變器引入基波的負序和零序擾動。而三相非線性負載也將給逆變器引入諧波的正序、負序和零序擾動。另外，實際情況中一些混合負載是不平衡和非線性負載組合而成的，此時將給逆變器的輸出電壓波形帶來更大的畸變[1,2]。

為改善不平衡非線性負載給輸出電壓波形帶來的嚴重畸變，目前已出現了較多的控制策略和拓撲[3]。文獻[4-11]在dq0坐標系下對輸出電壓進行諧波補償和不平衡控制，主要針對某次諧波例如5次、7次等進行補償控制，但控制環路和控制參數過多，會增加DSP的處理時間；文獻[12-14]根據三相四橋臂逆變系統的控制傳遞函數、期望的極點分布和性能指標進行單電壓環的設計，但缺乏電流環的控制，不利于對電流的動態控制；文獻[15-19]分別運用空間矢量、線性矩陣不等式等控制方法，增加了額外的控制電路，會降低DSP的執行速度，雖然三相電壓的平衡度和正弦度得到了改善，但負載切換時的動態特性仍然有待提高。

另外，關于不平衡非線性負載情況下的控制器設計一直是PWM逆變器領域的研究熱點。無差拍控制器[20,21]根據系統的狀態方程和輸出信號的反饋量計算逆變器的下一個采樣周期的脈沖寬度，但系統增益大，導致系統的抗干擾和穩定性降低；重復控制[22,23]利用擾動的“重復性”和“記憶”擾動發生的位置，實現對給定信號的跟蹤，但重復控制器結構存在周期延時環節，動態性能受到限制。電壓、電流PI雙環控制器[24,25]形式簡單，PI參數易于設置，電壓外環可以保證優良穩態特性，電流內環可以顯著提高系統的動態性能，及時消除負載擾動的影響。

雖然不平衡非線性負載在小功率場合的研究已經取得一些成果，但控制策略的實現和控制器的設計相對復雜，并且在混合負載切換時動態調整時間較長。本文首先基于廣義狀態空間平均法對三相平衡阻性負載下的三相三線制逆變器進行準確的建模和PI雙環控制器的設計，然后在dq0坐標系下利用電感電流滑動平均方法將PI雙環控制器推廣到三相不平衡負載和非線性負載，最后通過實驗樣機上的對比實驗，驗證了所提建模和控制方法改善三相電壓的平衡和負載切換時動態特性的有效性和準確性。

1 單個三相逆變器的建模

1.1 基于傳統狀態空間平均法的建模

三相三線制電壓型逆變器原理如圖1所示。定義開關函數為

式中，∈{a, b, c}；∈{p, n}。而且sp+sn=1。特殊地，令s=sp=1-sn。

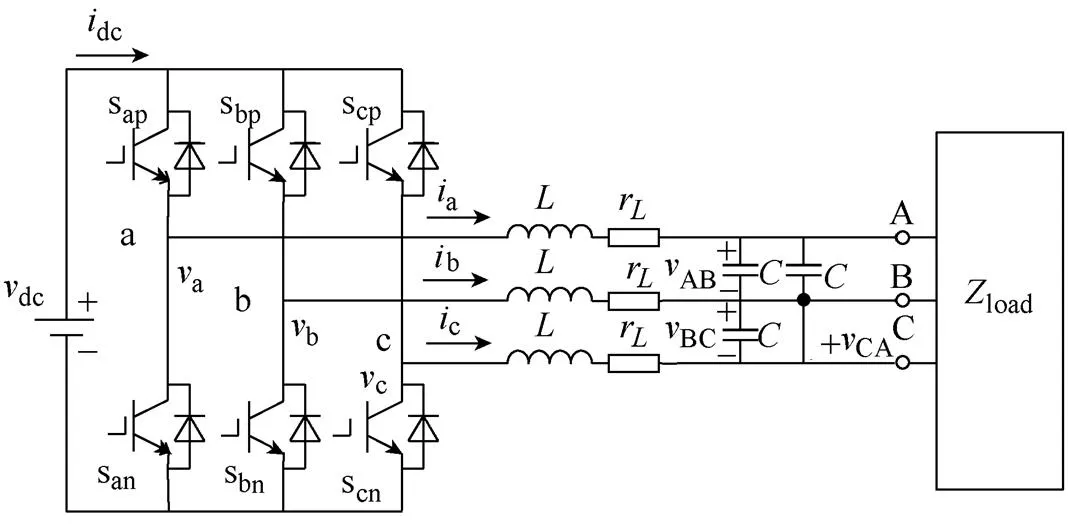
圖1 三相三線制電壓型逆變器原理

假設負載為三相對稱△連接，阻值為，則得到三相三線制逆變器交流側的方程為

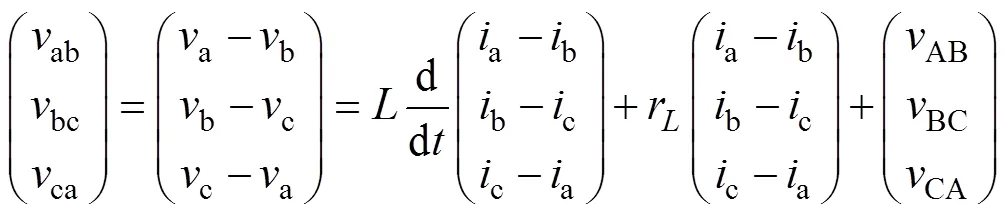
式（2）中左邊為虛擬線電流，定義為

交流側電壓和直流側電壓的關系為

聯立式（1）～式（4），得到

式中，為濾波電感；為濾波電容；r為濾波電感的等效串聯電阻；ab、bc、ca和AB、BC、CA分別為虛擬線電流和輸出線電壓的狀態變量。

為簡化模型，需要忽略電壓、電流等電量的開關頻率及其邊頻帶、開關頻率諧波與其邊帶，引入開關周期平均算子的定義

式中，()是狀態變量中的某一個；S為開關周期。對電壓、電流等電量進行開關周期平均運算，將保留原信號的低頻部分，而濾除開關頻率分量、開關頻率諧波分量及其邊頻分量。對式（5）兩邊進行開關周期平均，得到

式中

對式（7）進行dq0變換，在三線系統中，0軸分量幾乎為零，可忽略不計，于是得到dq0坐標下的單個三相逆變器的開關平均模型為

式中

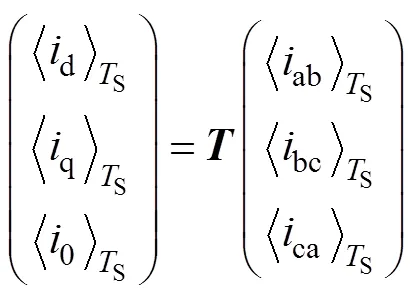
式中，為基波角頻率，=2p=100p。

三相電壓型逆變器在dq0坐標系的開關周期平均模型在穩態工作點附近經過小信號擾動和線性化，得到其dq0坐標下的小信號模型為

1.2 基于廣義狀態空間平均法的建模

廣義狀態空間平均法以傅里葉變換為基礎，若時域周期信號()滿足，則在時間區間（-,）內，()的傅里葉變換為

式中，=2p為信號的基波角頻率；為信號的階傅里葉變換系數，可以通過傅里葉反變換在一個工頻周期內的平均運算得到

廣義狀態空間平均法建模用到傅里葉變換的兩個重要特性：

（1）傅里葉變換系數的微分特性。第階傅里葉變換系數對時間的微分為

（2）卷積特性。兩個時域信號乘積的傅里葉變換系數等于單個信號所對應的傅里葉變換系數的離散卷積

若采用SPWM調制技術，可采用每一個開關周期內s的平均值構成的波形的基波d來代替s，則得到三相開關函數的基波交流分量為

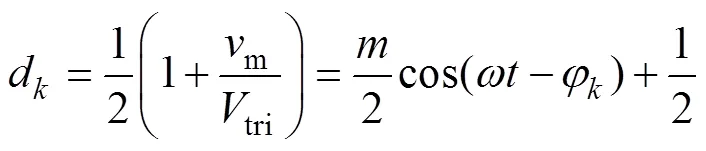
式中，分別為a=0、b=0+2p3和c=0-2p3；為基波角頻率；0為初始相位角；為幅值調制比。將式（18）代入式（5），得到

廣義狀態空間平均模型的狀態變量為信號的傅里葉系數，因此，若對上式中的狀態變量作一階近似，則有

結合式（16）、式（19）和式（20），可得到三相三線制逆變器的廣義狀態空間平均模型為

可認為直流輸入電壓dc恒定不變，即

若令

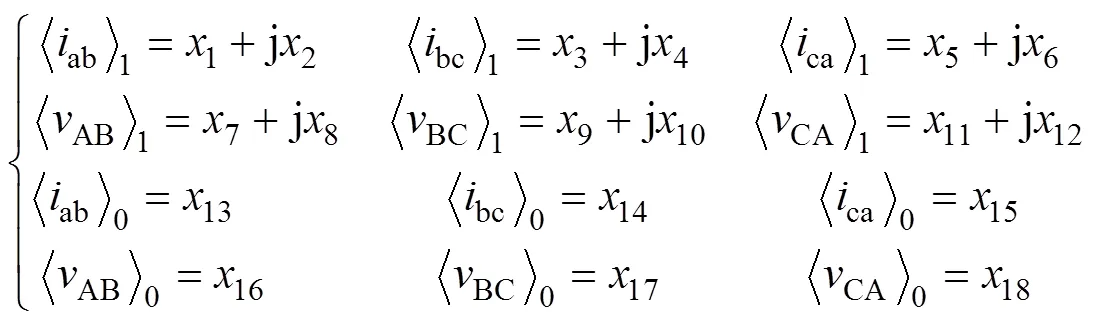
結合式（20）和式（23），得到

結合式（15）、式（17）、式（21）和式（23），并分離一階信號的實部和虛部，整理得到系統的廣義狀態空間平均模型為

考慮死區效應[26]，則輸出線電壓基波與理想基波之比為

式中，=8cd/(p)，c為開關頻率，d為死區時間，為幅值調制比；為負載的功率因數角。

要強調的是，實驗平臺中的逆變器輸出端接有LC濾波器以便濾除開關頻率及其倍數的諧波。但由于LC濾波器的截止頻率設計為2kHz，是基波頻率50Hz的40倍，在考慮死區效應時，濾波電感和電容的存在對基波電壓的影響很小，可忽略不計。

同理，虛擬線電流基波也有式（26）的比例關系

現在僅考慮阻性負載，則=0，式（26）和式（27）簡化為

在實際應用中，輸出電壓一般會加入直流抑制環節或逆變橋的輸出端和負載之間有隔離變壓器，所以式（21）關于輸出電壓直流成分的方程可忽略不計。將=/(1-)、=/(1-)代入式（21）關于基波成分的方程，得到

若令

同理，經過若干變換后，得到考慮死區效應后，系統的廣義狀態空間平均模型為

經過一階近似后，三相逆變器的狀態變量可用其基波成分代替，為了簡便，電壓和電流的基波成分仍沿用狀態變量的符號，其在abc坐標系下的方程為

經dq0變換，并在穩態工作點附近進行小信號擾動和線性化，得到基于廣義狀態空間平均法的小信號模型為

式中

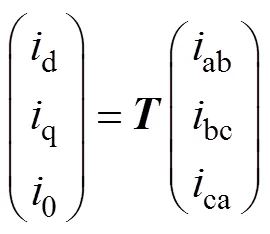
上文中，對三相三線制電壓型逆變器進行了兩種不同方法的建模，得到了基于不同方法的小信號模型。

傳統狀態空間平均法對狀態變量進行開關周期平均運算，雖然原信號的開關頻率分量、開關頻率諧波分量及其邊頻分量得到了濾除，但是保留下來的低頻部分仍然可能包括5、7、11、13等低次的工頻諧波。在考慮死區時間的影響時，濾波電感和電容的存在對低次工頻諧波的影響也會不同，建模的過程非常繁瑣。在實際情況中，主要關心的是狀態變量的基頻分量，在建模過程中一般不考慮低次的工頻諧波。

廣義狀態空間平均法以傅里葉變換為基礎，利用微分特性和卷積特性對狀態變量進行了一階近似，保留了狀態變量中的基頻分量，濾除了狀態變量中的其他諧波分量。在考慮死區效應時，濾波電感和電容的存在對基頻分量的影響可忽略不計，可以對其進行有效而簡便的建模。因此，廣義狀態空間平均法的小信號模型更接近實際情況，由此設計的控制參數能夠直接應用于實驗調試中。

2 基于廣義平均法的雙環PI控制器的設計

本實驗平臺的控制框圖如圖2所示。

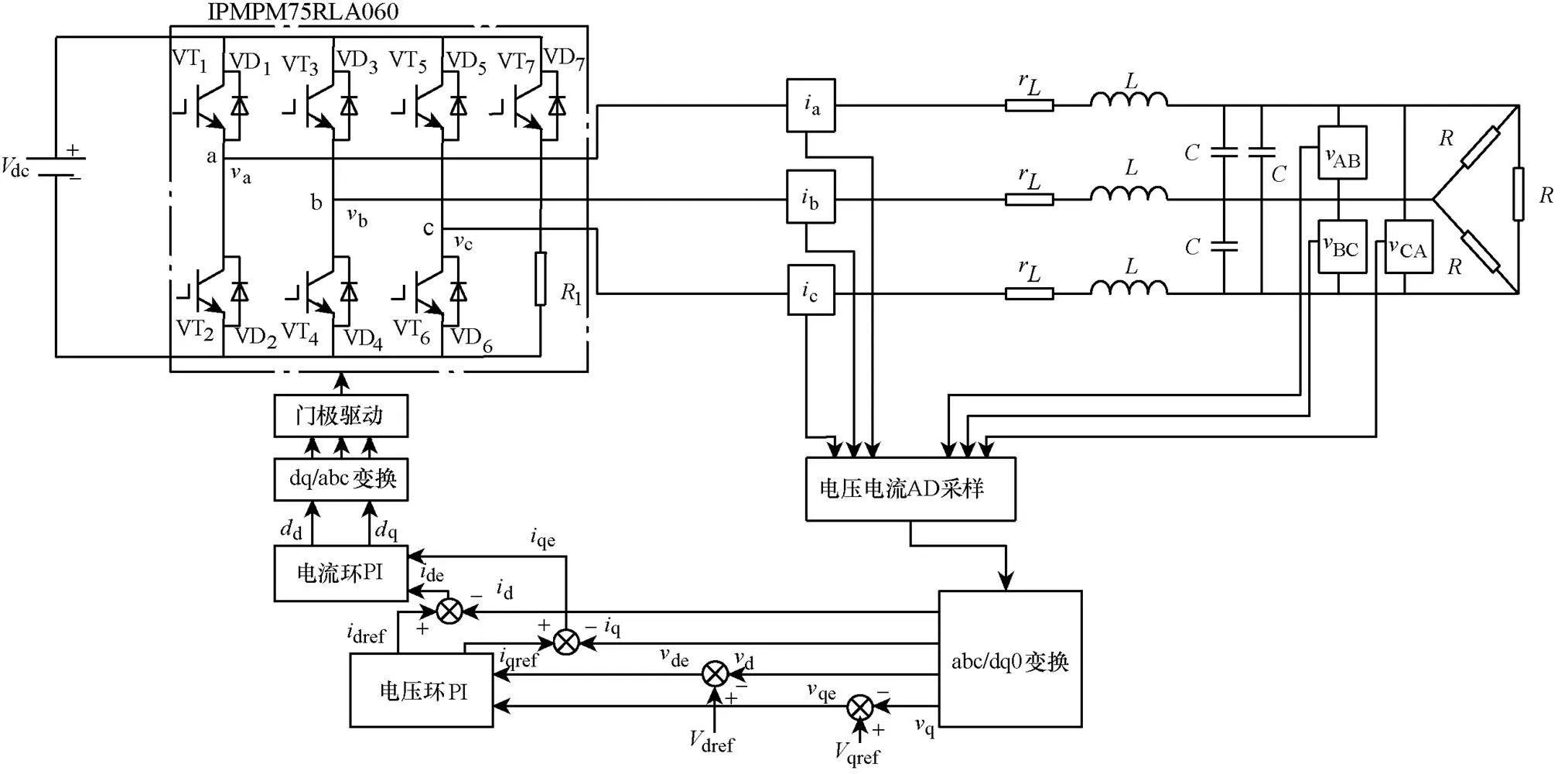
圖2 三相三線制逆變器控制框圖

在實驗平臺中，dc=250V，電感=3.4mH，電感ESRr=0.2W，=70W、=2.2mF。程序中電壓參考值dref=150V，qref=0V，系統穩定時的幅值調制比=dref/(0.866dc)=150/(0.866×250)=0.693。另外，=8cd/(p)=8×2×104×2×10-6/(0.693p)=0.147（式中，c=20kHz、d=2μs）。

三相逆變器輸出電壓變化相比電流較慢，在設計電流內環時可認為此時，將其代入式（33），得到

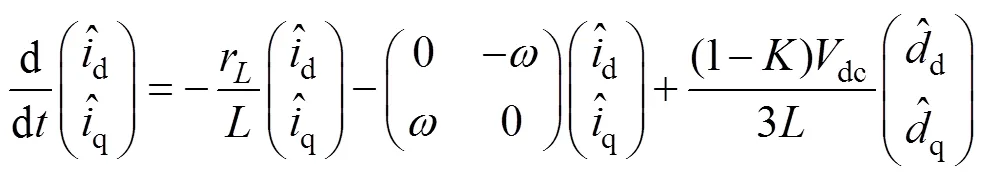
控制模塊采用PI調節，其傳遞函數為

對d、q軸之間的耦合關系進行解耦后，得到加入PI控制器的電流內環閉環傳遞函數為

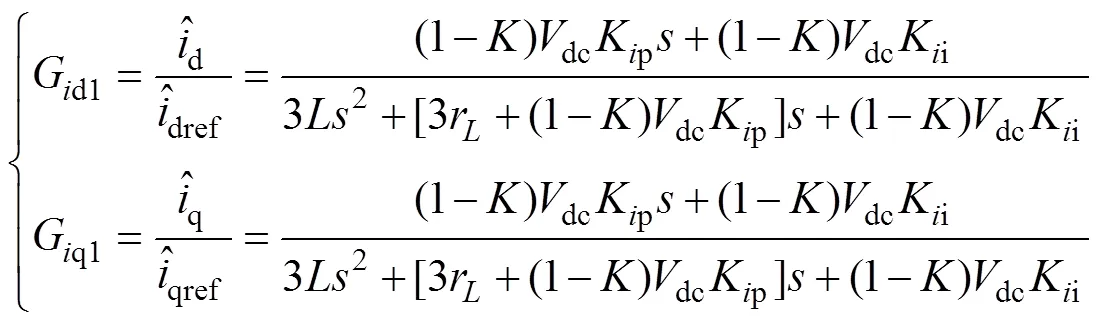
為了緊密跟蹤逆變器的狀態變化，改善逆變器的動態性能，取電流環閉環函數的截止頻率為開關頻率的1/10，即2kHz，代入相關數據，得到電流內環PI控制器的PI參數：Kp0.2、Ki10。加入PI控制后的電流內環閉環伯德圖如圖3所示。

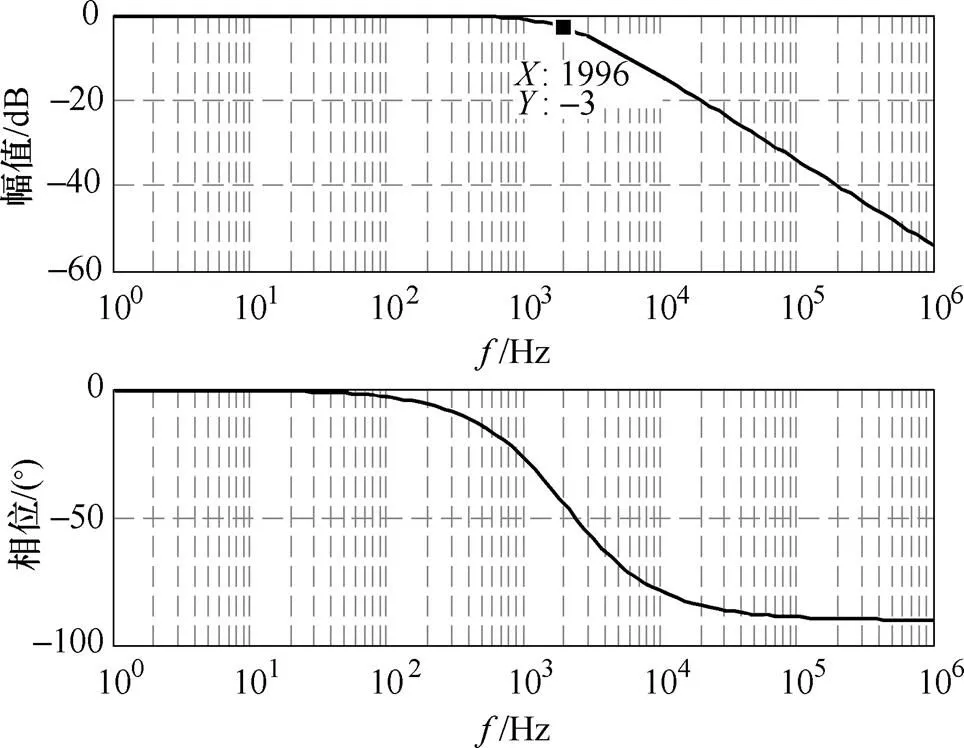
圖3 電流內環伯德圖

在設計電壓外環控制器時，電流內環可用單位增益代替。由式（33），得到

控制模塊采用PI調節，其傳遞函數為

對d、q軸之間的耦合關系進行解耦后，得到加入PI控制器的電壓外環閉環傳遞函數為

為提高系統穩定性和抑制高頻諧波，加入PI控制環節后的電壓外環閉環傳遞函數的截止頻率設為200Hz，代入相關數據，得到電壓外環PI控制器的PI參數為Kp0.01、Ki54。加入PI控制后的電壓外環閉環伯德圖如圖4所示。

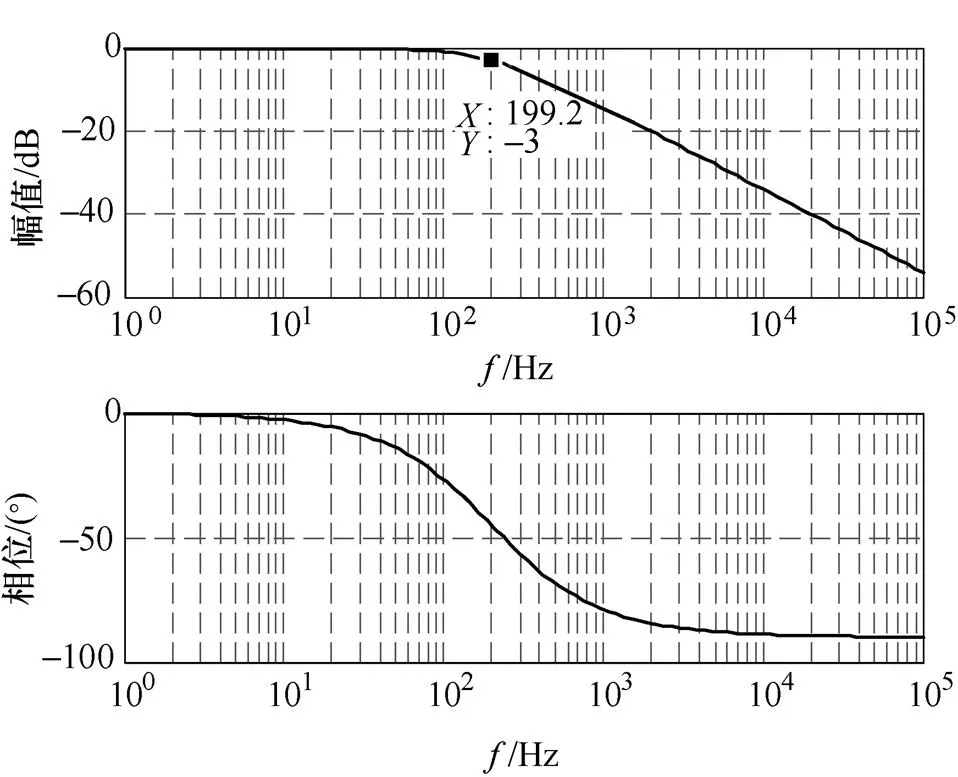
圖4 電壓外環伯德圖

在上述PI控制器設計中，由于第1.2節中的廣義狀態空間平均模型考慮了死區時間的影響，基于此模型計算的電壓外環和電流內環PI控制參數更接近實際情況，PI參數能夠直接應用于實驗平臺中，實驗的調試得到簡化。

3 電感電流滑動平均算法的引入

第2節的PI控制器是基于三相平衡負載設計的，但當逆變器帶不平衡非線性負載時，系統內的電流會增加基波的負序分量和諧波分量（三線制中不存在零序分量，本文暫不考慮）。

根據對稱分量變換和傅里葉分解，帶不平衡非線性負載時的電感電流可寫為

式中，基波的正序分量、負序分量和諧波分量分別為

經過dq0變換后，上述各分量變為

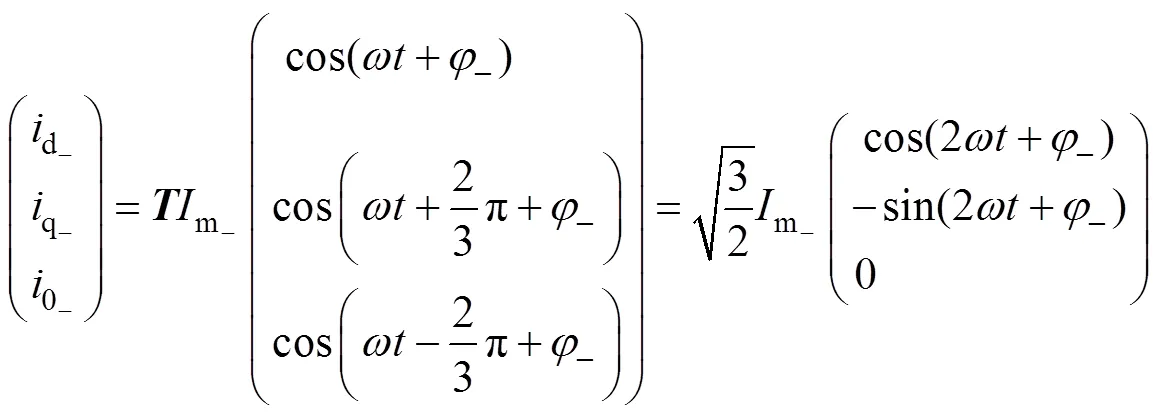
由以上三式可知，帶不平衡非線性負載時，電感電流的d分量和q分量不再是直流量，第2節中設計的PI控制器將不再適用。但值得注意的是，電流的基波負序分量和諧波分量是交流量，可通過平均的方法將其消除，得到的仍是基波正序分量的dq分量。

在本實驗中，每個開關周期采樣（電壓和電流）一次。常規的平均方法是周期平均，考慮電感電流的周期性，在一個工頻周期內對電感電流采樣值的瞬時dq序列求平均，即得到其中的直流分量

式中，=400，表示一個工頻周期采樣400次。此方法中，每個工頻周期僅計算一次電感電流平均值，不能實時地反映電感電流的變化，計算的延遲時間較長，會影響逆變器系統的動態特性。

滑動平均的引入是為了在實現低通濾波的同時保證系統的動態性能。針對電感電流采樣值的瞬時dq序列，構建一個點數為400的滑動窗口。從dq序列的第1個點開始，一直累加到第個點，然后取平均，即可得到第個點的電感電流采樣值的平均dq序列，即

式（50）考慮了電感電流瞬時dq序列中的交流信號在每個工頻周期的重復性。在實際應用中，當采樣第個點時，可考慮用當前新的信息代替一個工頻周期前同一位置的信號，得到遞歸式

式中，()為當前時刻的電感電流新信息；()為上一個周期對應當前時刻的電感電流舊信息。一旦電流信號發生變化，滑動平均得到的數值也會隨之變化，逼近于真實值。相對于周期平均法要在一個周期后才能得到真實值，減小了計算的延遲時間。

另外，由式（51）可知，每個dq序列點都只計算了兩次，而不用考慮滑動窗口的長度。另外，整個計算過程中僅用了一次加法、一次減法和一次乘法，執行速度相當快。相對而言，滑動平均算法比其他數字濾波器的算法都快。

綜上所述，滑動平均算法在每個采樣周期中計算一次電流平均值，能夠實時地反映電感電流信號的變化趨勢，并且每次處理的數據點和運算次數很少，執行速度比較快，能夠在實現低通濾波的同時，較快地跟蹤電流的變化，改善系統在負載變化時的動態特性。

此外，由式（47）和式（48）可知，電流中的基波負序分量和諧波分量在dq0坐標系下的dq分量都是以偶次諧波的形式出現，對于滑動平均，窗口長度可縮短為原來的1/2。針對三相不控整流負載，電流中的6-1次負序諧波和6+1次正序諧波在dq軸上以6脈波的形式出現，此時，窗口的長度可進一步縮短為原來的1/6。

4 實驗結果與分析

為驗證本文基于廣義狀態空間平均法設計的PI控制器和電感電流滑動平均的有效性，在三相三線制逆變器實驗平臺上進行了不平衡非線性負載的穩態和動態實驗。其中，非線性負載由三相整流橋、電容non和電阻non并聯而成。具體參數見下表。

表 系統參數

圖5、圖6分別為不平衡負載和非線性負載時的電壓、電流穩態波形。由圖可知，在不平衡非線性的負載條件下，本文的控制策略能夠保證逆變器輸出平滑對稱的三相電壓。圖7a和圖8a是運用本文的建模方法和控制策略的切載波形。在同樣的負載切換條件下，采用基于傳統狀態空間平均法優化設計后的PI參數和電感電流周期平均的控制策略，進行了相應的實驗，實驗波形如圖7b和圖8b所示。其中，圖8中的混合負載由非線性負載和不平衡負載（70W, 140W, 140W）并聯而成。

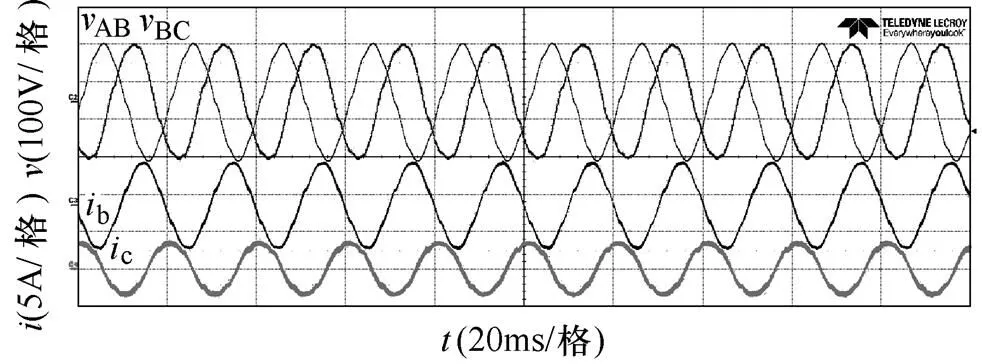
圖5 不平衡負載時的電壓、電流穩態波形（35W,70W,70W）

圖6 非線性負載時的電壓、電流穩態波形

圖7 不同控制策略下，不平衡負載時（70W,140W,140W）切（35W,70W,70W）的電壓、電流瞬態波形

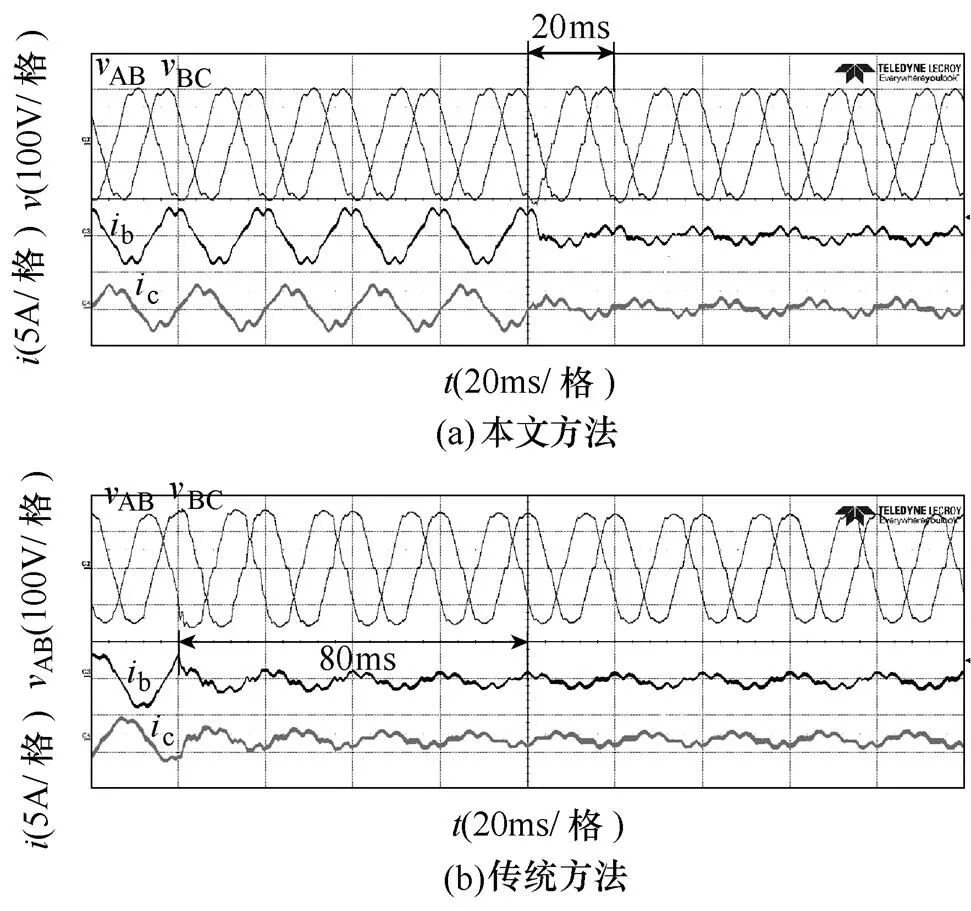
圖8 不同控制策略下，混合負載時的電壓、電流瞬態波形（混合負載切非線性負載）

由圖7可知，在不平衡負載半載切換到滿載的情況下，采用基于本文建模方法設計的PI參數和控制策略時，電壓的大小基本保持不變，電流在一個工頻周期內可恢復穩定。而傳統方法的電壓會有所減小，電壓、電流重新恢復需要3個工頻周期以上。

同樣地，由圖8可看出，在混合負載切換到非線性負載的情況下，采用基于本文建模方法設計的PI參數和控制策略時，電壓和電流在一個工頻周期內可恢復穩定。而傳統方法的電壓會有所增加，電壓、電流重新恢復需要4個工頻周期。

圖7和圖8的對比實驗證明了本文的建模方法和控制策略在改善系統動態特性上的準確性和有 效性。

5 結論

本文首先基于廣義狀態空間平均法對三相三線制逆變器進行了準確的建模，在模型基礎上對PI雙環控制器進行了dq0坐標系下的設計，設計的PI控制參數更接近于實際情況，能夠直接應用于實驗中。采用電感電流滑動平均方法，在把所設計的PI控制器推廣到不平衡非線性負載的同時，保證了系統的動態性能。在三相三線制逆變器實驗平臺上，進行了本文方法和傳統方法的對比實驗，結果表明，在不平衡非線性負載下，本文的建模方法和控制策略能夠在保證逆變器輸出平滑對稱的三相電壓的同時，較大地改進了負載切換時系統的動態特性。

[1] Hamzeh M, Ghazanfari A, Mokhtari H, et al. Integrating hybrid power source into an islanded MV microgird using CHB multilevel inverter under unba- lanced and nonlinear load conditions[J]. IEEE Trans- actions on Energy Conversion, 2013,28(3): 643-651.

[2] 胡媛媛. 三相三線逆變器數字控制系統研究[D]. 武漢: 華中科技大學, 2008.

[3] 陳敏. 非線性負載條件下的逆變器特性研究[D]. 杭州: 浙江大學, 2006.

[4] Dehghan S M, Ahmad A A, Lourakzadegan R, et al. A high performance controller for parallel operation of three-phase UPSs powering unbalanced and nonlinear loads[C]. Power Electronics, Drive Systems and Technologies Conference, Tehran, Iran, 2011: 433-438.

[5] Kim K H, Park N J, Hyun D S. Advanced synchronous reference frame controller for three-

phase UPS powering unbalanced and nonlinear loads[C]. IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 2005: 1699-1704.

[6] Gannett R A, Sozio J C, Boroyevich D. Application of synchronous and stationary frame controllers for unbalanced and non-linear load compensation in 4-leg inverter[C]. Applied Power Electronics Conference, Dallas, America, 2002: 1038-1043.

[7] Lohia P, Mishra M K, Karthikeyan K, et al. A minimally switched control algorithm for three-phase four-leg VSI topology to compensate unbalanced and nonlinear load[J]. IEEE Transactions on Power Electronics, 2008, 23(4): 1935-1944.

[8] 霍群海, 孔力, 唐西勝. 微源逆變器不平衡非線性混合負載的控制[J]. 中國電機工程學報, 2010, 30(15): 10-15.

Huo Qunhai, Kong Li, Tang Xisheng. Control strategy for unbalanced and nonlinear mixed load of micro-source inverter[J]. Proceedings of the CSEE, 2010, 30(15): 10-15.

[9] Paridari K, Hamzeh M, Emamian S, et al. A new decentralized voltage control scheme of an autonomous microgrid under unbalanced and nonlinear load conditons[C]. IEEE International Conference on Industrial Technology, Cape Town, South Africa, 2013: 1812-1817.

[10] Mishra M K, Karthikeyan K. An investigation on design and switching dynamics of a voltage source inverter to compensate unbalanced and nonlinear loads[J]. IEEE Transactions on Industrial Electronics, 2009, 56(8): 2802-2810.

[11] Geddada N, Karanki S B, Mishra M K, et al. Modified four leg DSTATCOM topology for compensation of unbalanced and nonlinear loads in three phase four wire system[C]. Proceedings of European Conference on Power Electronic and Applications, Birmingham, UK, 2011: 1-10.

[12] 王正仕, 林金燕, 陳輝明, 等. 不平衡非線性負載下分布式供電逆變器的控制[J]. 電力系統自動化, 2008, 32(1): 48-51, 60.

Wang Zhengshi, Lin Jinyan, Chen Huiming, et al. Control of distributed power inverter with unbalanced and nonlinear loads[J]. Automation of Electric Power Systems, 2008, 32(1): 48-51, 60.

[13] 林金燕. 不平衡負載和非線性負載下逆變器的研究[D]. 杭州: 浙江大學, 2007.

[14] 林金燕, 王正仕, 陳輝明, 等. 一種高性能三相四橋臂逆變器控制器的設計[J]. 中國電機工程學報, 2007, 27(22): 101-105.

Lin Jinyan, Wang Zhengshi, Chen Huiming, et al. High performance controller design for three-phase four-leg inverters[J]. Proceedings of the CSEE, 2007, 27(22): 101-105.

[15] Borup U, Enjeti P N, Blaabjerg F. A new space-vector- based control method for UPS systems powering nonlinear and unbalanced loads[J]. IEEE Transactions on Industrial Electronics, 2001, 37(6): 1864-1870.

[16] 孫馳, 畢增軍, 魏光輝. 一種新穎的三相四橋臂逆變器解耦控制的建模與仿真[J]. 中國電機工程學報, 2004, 24(1): 124-130.

Sun Chi, Bi Zengjun, Wei Guanghui. Modeling and simulation of a three-phase four-leg inverter based on a novel decoupled control technique[J]. Proceedings of the CSEE, 2004, 24(1): 124-130.

[17] Delghavi M B, Yazdani A. Islanded-mode control of electronically coupled distributed-resource units under unbalanced and nonlinear load conditions[J]. IEEE Transactions on Power Delivery, 2011, 26(2): 661-673.

[18] Emamian S, Hamzeh M, Paridari K, et al. Robust decentralized voltage control of an islanded microgrid under unbalanced and nonlinear load conditions[C]. IEEE International Conference on Industrial Technology, Cape Town, South Africa, 2013: 1825-1830.

[19] Moses P S, Masoum M A S. Three-phase asymmetric transformer aging considering voltage-current harmonic interactions, unbalanced nonlinear loading, magnetic couplings, and hysteresis[J]．IEEE Trans-

actions on Energy Conversion, 2012, 27(2): 318-327.

[20] He Yingjie, Liu Jinjun, Tang Jian, et al. A novel deadbeat control method for active power filters with three-level NPC inverter[C]. IEEE Power Electronics Specialists Conference, Rhodes, Greece, 2008: 661-

665.

[21] Oettmeier M, Heising C, Staudt V, et al. Dead-beat control for a single-phase 50kW, 16.7Hz railway-grid representation inverter featuring variable grid parameters[C]. International Conference on Power Engineering, Energy and Electrical Drives, Lisbon, Portugal, 2009: 279-284.

[22] Chen Dong, Zhang Junming, Qian Zhaoming, et al. An improved repetitive control scheme for grid-

connected inverter with frequency-adaptive capabi-

lity[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 814-823.

[23] Toms H, Zhong Qingchang. A current-control strategy for voltage-source inverters in microgrid based on H∞and repetitive control[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 943-952.

[24] Ma Xuejun, Wu Hongxia, Sun Song, et al. Control method with digital PI dual close-loop for inverter[C]. International Conference on Electrical Machines and Systems, Seoul, Korea(South), 2007: 102-105.

[25] Liu Cheng, Li Wenjuan, Pang Songlin, et al. Saber simulation and experimental research on single-phase digital inverter with PI control[C]. International Conference on Measurement, Information and Control, Harbin, China, 2012: 548-552.

[26] 林釗, 馬皓, 尹藝迪, 等. 三相三線制SPWM逆變器死區效應分析[J]. 機電工程, 2012, 29(9): 1090-1094.

Lin Zhao, Ma Hao, Yin Yidi, et al. Analysis of dead-time effect for three-phase three-wire SPWM inverter[J]. Journal of Mechanical & Electrical Engineering, 2012, 29(9): 1090-1094.

Modeling and Control of Three-Phase Inverter Powering Unbalanced and Nonlinear Loads

（Zhejiang University Hangzhou 310027 China）

In order to diminish the influence of unbalanced and nonlinear loads on the output voltage quality of three-phase inverter in practical applications and further improve the dynamic characteristic under different load switching, modeling method based on generalized state space average and a novel control strategy based on inductor current moving average are proposed. Based on generalized state space averaging method, an accurate model of inverter with balanced load and design of PI controller in the dq0 synchronous rotating coordinate is analyzed in detail. Moreover, inductor current moving averaging method is presented, adjusting the PI controller applicable to three-phase unbalanced and nonlinear loads. Compared with conventional method, the proposed model and control strategy can preferably improve dynamic characteristics under different load switching. Moreover, it can guarantee the balance of three-phase voltages with mixed loads.

Unbalanced and nonlinear loads, three-phase three-wire inverter, generalized state space averaging method, dq0 transformation, inductor current moving average

TM464

馬 皓 男，1969年生，博士，教授，研究方向為電力電子技術及其應用、電力電子先進控制技術和電力電子系統故障診斷。

林 釗 男，1990年生，碩士研究生，研究方向為逆變器并聯及網絡控制。

2013-09-22 改稿日期 2013-12-05

國家自然科學基金（51177149）和浙江省重點科技創新團隊項目（2010R50021）資助。