動態規劃人員分配算法研究
鄧競偉
(西北民族大學數學與計算機科學學院,蘭州 730030)
動態規劃人員分配算法研究
鄧競偉
(西北民族大學數學與計算機科學學院,蘭州730030)
0 引言
近年來,突發事件頻繁發生,對突發事件的應急管理也引起了國家的高度重視,例如,2014年,云南魯甸6.5級地震災害,9月重慶洪澇災害,新疆和田7.3級地震災害動態規劃在許多領域中得到越來越廣泛的應用,例如經濟領域、工程技術領域、交通領域等,特別是在世界各地的資源分配中應用更為普遍。在資源分配中應用動態規劃可以使資源得到充分的應用,可以得到更大的效益。用動態規劃解決資源分配問題是把復雜的問題劃分為若干個階段,并逐步解決,最終達到全局最優[1]。Dechter等人分析了常用的Floyd-Warshall算法[2],從二十世紀五十年代初美國數學家R.E.Bellman[3]等在研究多階段決策過程的優化問題時,提出了著名的最優化原理。現實生活中已經證明許多問題用動態規劃求解比用線性規劃更有效[4]。經過多年的科研發展和實際應用,動態規劃日益完善。近幾年,在我國動態規劃應用越來越普遍,例如:1991年,林學鈦[5]等對平頂山市地表水和地下水的聯合管理研究中,運用動態規劃方法對白龜山水庫進行優化調度,取得了良好的效果。實踐證明,將最短路徑問題、資源分配利用、排序等問題,運用動態規劃比其他方法更為方便。我們研究資源分配應用中的優、缺點,能夠使資源得到充分利用,提高資源利用率并創造更大的利潤,可以為動態規劃在其他領域的應用中提供了很好的幫助。
1 算法實現
在人工智能領域中,現實生活中的大多數問題可以轉化為約束滿足規劃調度問題來解決[4-5]。動態規劃應用十分廣泛,本文主要研究動態規劃在資源分配中的應用,建立模型是解決資源分配問題的方法之一。數學模型是指對于現實世界的一個特定對象,為了一個特定目標,根據特有的內在規律,做出一些很有必要的假設,運用適當的數學工具得到的一個數據結構[5-6]。
動態規劃系統的最優化是用來解決具有一定序列的確定性系統和隨機性系統等的最優化問題。最優化決策是不考慮初始狀態的,根據最優化過程以相反的順序進行的特點,因此,對系統的每個元素按同樣的順序進行編寫號碼。建立一個合理的動態規劃模型,需要從以下幾個方面進行考慮:
(1)把問題按時間的先后順序劃分為若干個階段,選出階段變量,這些階段必須是有順序的。
(2)選出狀態變量,因為狀態變量能夠表示整個過程的狀態轉移規律。
(3)選出決策變量,然后,根據狀態之間的遞推關系得出最終的狀態轉移方程。
(4)建立指標函數和列出動態規劃方程,給出最終條件;然后,用逆推的方法推出各個階段的最優決策,再按順序求出整個問題的最優決策,動態規劃的基本方程的逆序形式為[6]:
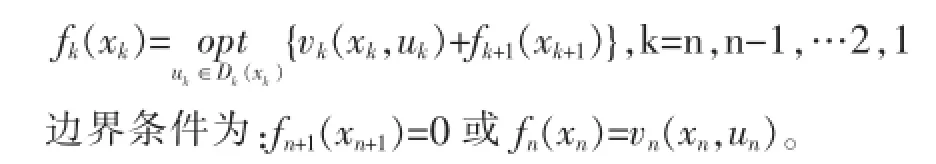
在具體求解時,從邊界條件n=k開始,從前向后逆推逐個階段求出最優決策和每個過程的最優值,一直到求出f1(x1)的解就是計算具體問題的最優解。
2 具體實例
根據具體實例來分析動態規劃在資源分配中的具體應用。例如,某一個公司有A、B、C,3個車間,現在此公司有4位員工要分配到3個車間,已知各個車間獲得這種設備所能創造的利潤,如表1所示:

表1 員工數與創造的利潤
此時,考慮如何將這4位員工分配到3個車間才能使此公司得到最大的利潤。
首先,假設3個車間分別為A、B、C,其中,x表示從第i個車間分配到第j個車間的員工數,xi表示分配到第i個車間的員工總數,由此可以得到,從第i+1個車間分配到第j個車間的員工總數為:xi+1=x-xi;fi(x)表示將x位員工從第i個車間分配到第j個車間所得到的利潤;gi(xi)表示將xi位員工分配到第i個車間所得到的利潤。因此,可以得出動態規劃模型為:

當i=3時,就是把4位員工都分給第3車間,

同理,當i=2時,就是把4位員工分給第2和3車間,
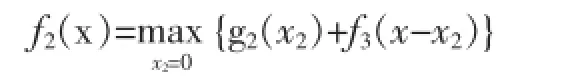
那么當x=0時,
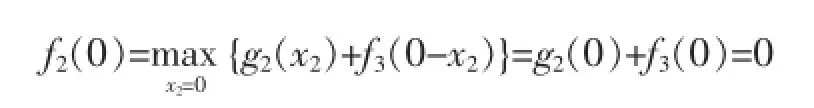
此時最優決策方案為:d2(x2)=0。
當x=1時,
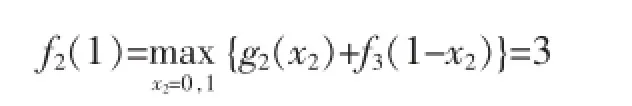
此時最優決策方案為:d2(x2)=1。
當x=2時,
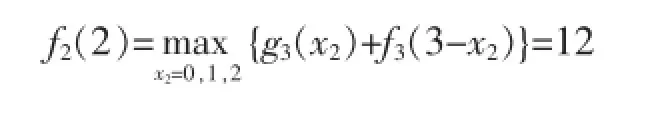
此時最優決策方案為:d2(x2)=2。
當x=3時,
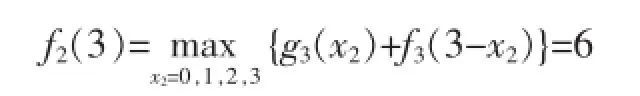
此時最優決策方案為:d2(x2)=0。
當x=4時,
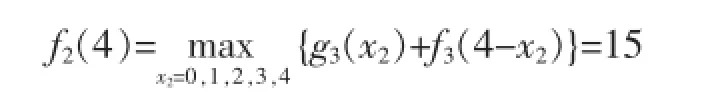
此時最優決策方案為:d2(x2)=1。
當i=1時,即將公司員工分配給第1和2車間;

同理可得:
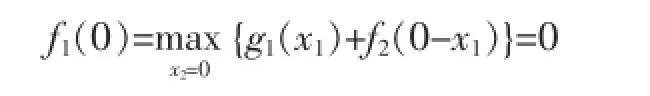
此時最優決策方案為:d2(x2)=0。
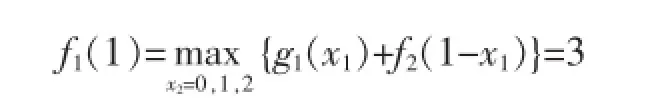
此時最優決策方案為:d2(x2)=0。
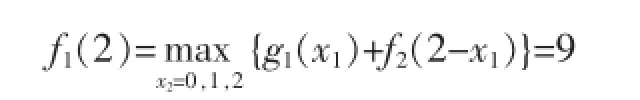
此時最優決策方案為:d2(x2)=0。

此時最優決策方案為:d2(x2)=0或1。

此時最優決策方案為:d2(x2)=2。
因此,可以看出最優分配方案有兩種:
第一種:第1個車間不分配員工,4位員工分別分配給第2和3車間,當i=2時,發現f2(4)的最優規劃決策方案所得利潤最高。所以,應分配1位員工到第2車間,分配3位員工到第3車間。
第二種:第3個車間不分配員工,4位員工分別分配給第1和2車間,當i=1時,發現f1(4)的最優規劃決策方案所得利潤最高。所以,應分配2位員工到第1車間,分配2位員工到第2車間。
從上面分析可以看出,在這兩種分配方案中,A、B、C,3個車間的總效益都是15。
3 結語
動態規劃在資源分配中已經被廣泛應用,這說明動態規劃是在解決資源分配這類問題的有效方法。在資源的分配決策中,動態規劃使得資源的利用率最高,避免了資源的浪費,從而可以使有限的資源創造出最大的經濟利潤。動態規劃的應用為我們解決了很多實際問題,對如何建立應急資源管理機制也具有很好理論基礎和現實意義。
[1]徐瑞,徐曉飛,崔平遠.基于時間約束網絡的動態規劃調度算法.計算機集成制造系統-CISM[J],2004.10(1):188-194.
[2]Muscettola N,Nayak P P,Pell B,Williams B.Remote agent:to boldly go where no AI system has gone before[J].Artificial Intelligence.1998.103(1-2):5-47.
[3]滕宇,梁方楚.動態規劃原理及應用[M].西南交通大學出版社.2011.12.
[4]袁佳樂,黃兆華,曹玉紅.動態規劃在資源分配上的應用.西安文理學院學報:自然科學版[J],2008,11(3):66-69.
[5]盧向南.應用運籌學[M].浙江大學出版社,2005.
[6]孫寶,王希云.基于MATLAB的動態規劃常用算法的實現.太原師范學院學報(自然科學版),2008,7(4):26-30.
Dynamic Algorithm;Policy Decision;Planning and Scheduling;Resource Allocation
Research on Dynamic Planning Assignment Algorithm
DENG Jing-wei
(School of Mathematics and Computer Science,Northwest University for Nationalities,Lanzhou 730124)
教育部人文社會科學研究青年基金項目(No.13YJCZH029、No.12YJCZH027)、中央高校基本科研業務費專項資金項目(No.31920150039)
1007-1423(2015)26-0046-03
10.3969/j.issn.1007-1423.2015.26.012
鄧競偉(1980-),女,甘肅蘭州人,碩士,研究方向為最優化理論、算法設計與分析
2015-08-04
2015-09-08
如何快速準確地進行資源調度是突發事件應急資源的重要研究問題,并且及時有效的資源供給促進救援工作的順利進行。動態規劃在許多領域中都得到十分廣泛的應用。介紹動態規劃方法、最優化原理和動態規劃模型,并通過實例進行分析和討論。
動態算法;決策;規劃調度;資源分配
How to carry out resource scheduling is the important research problem of the emergency resources,and the timely and effective resources supply to promote the smooth progress of the rescue work.Dynamic programming is widely used in many fields.Introduces the dynamic programming method,the optimization principle and the dynamic programming model,analyzes and discusses the examples.

