基于帶寬比例因子的導航信號帶寬優化

馬　煦，李春霞

（北京衛星導航中心，北京　100094）

基于帶寬比例因子的導航信號帶寬優化

馬煦，李春霞

（北京衛星導航中心，北京100094）

導航信號頻率帶寬日益成為各衛星導航系統建設者們競相搶奪的重要資源，信號帶寬優化有利于提高頻率利用率和多系統兼容性。本文提出了帶寬比例因子這一參量，針對BPSK，sinBOC，cosBOC信號，分析了其偽碼跟蹤精度、抗多徑性能、抗干擾性能隨帶寬比例因子變化的關系，并以這些性能優化為目標設計了優化的帶寬比例因子。結果表明，BPSK信號最優化的帶寬為主瓣寬度的0.8倍；sinBOC，cosBOC信號最優化的帶寬為±（fs+08Rc）。

帶寬比例因子；帶寬；精度跟蹤；多徑；抗干擾

1　引言

隨著世界衛星導航系統不斷發展，導航信號頻率日益成為各衛星導航系統建設者們競相搶奪的重要資源，美、歐、俄等世界衛星導航大國紛紛在國際頻率協調和談判會議上竭盡所能地搶占更多的頻率帶寬。在這種形勢下，優化設計信號帶寬無疑是一個充分利用頻率資源的好辦法。特別是在多系統之間存在頻段部分重疊的情況下，發射和接收帶寬的優化設計對系統間兼容性、各個信號接收性能最優化尤為關鍵。可以說，帶寬已成為繼發射頻率、調制方式、信息速率、編碼方案等之后又一新的信號設計要素。

國際上關于頻率資源協調和系統間兼容性優化，關注點主要側重于傳統信號設計要素包括頻點［1］，［2］、調制方式［3］等，對給定調制方式下的信號帶寬，多采用主瓣寬度這一默認值［4］，鮮有優化設計。

本文試圖尋找衛星導航信號帶寬的最優設計值。提出了帶寬比例因子這一參量，針對BPSK，sinBOC，cosBOC信號，分析了其偽碼跟蹤精度、抗多徑性能、抗干擾性能隨帶寬比例因子變化的關系，并以這些性能優化為目標設計了優化的帶寬比例因子。其中，偽碼跟蹤精度、抗多徑性能、抗干擾性能分別采用偽碼跟蹤熱噪聲誤差理論下限、典型多徑誤差、載波跟蹤抗干擾品質因數和偽碼跟蹤抗干擾品質因數來衡量。

2　導航性能與帶寬比率因子的關系

2.1帶寬比率因子

為了消除絕對帶寬的影響，提出帶寬比率因子這一新的參量來描述信號帶寬與主瓣寬度的關系。定義信號的帶寬比率因子為

式中，Br表示雙邊帶信號的帶寬；Rc表示偽碼信息速率。

2.2偽碼跟蹤精度與帶寬比率因子的關系

偽碼跟蹤誤差的Cremer-Rao下界為

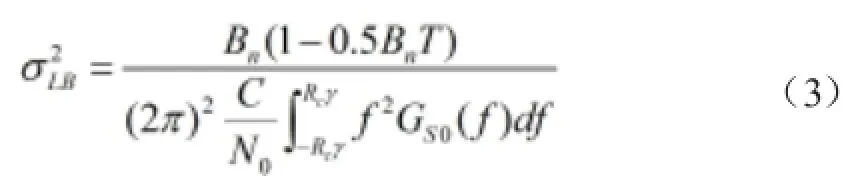
2.3抗多徑性能與帶寬比率因子的關系

（1）多徑誤差包絡

為簡便記，討論僅存在一路多徑信號的情形，多徑誤差量可用如下方程表達：

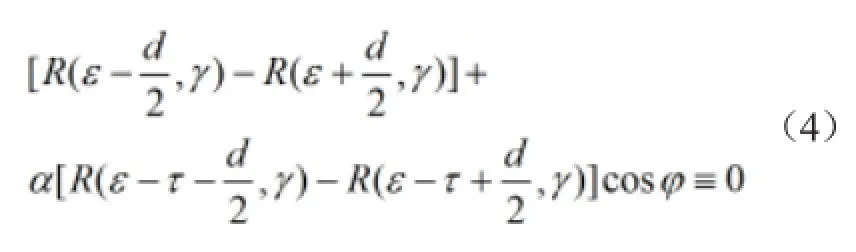
式中，R（·，·）表示碼相關函數，它與時延和信號帶寬有關；ε表示多徑誤差；d表示碼環鑒相器超前碼與滯后碼之間的間隔；分別表示多徑信號相對直達信號的幅度、時延和相位。

（2）多徑誤差包絡的期望

多徑信號不同幅度和時延發生的歸一化概率密度函數如下［7］，［8］

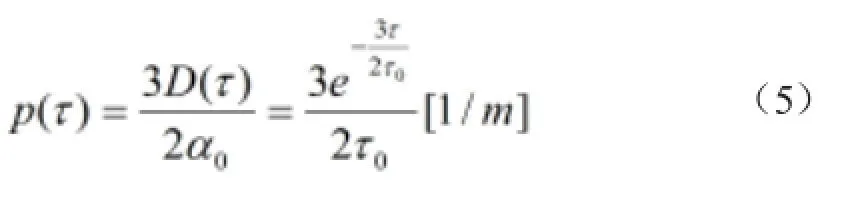
結合多徑發生概率和多徑誤差包絡，可以得出考慮近距離多徑比遠距離多徑信號進入接收機的概率更高這一事實的多徑包絡期望，用來描述典型的多徑誤差。典型的多徑誤差可通過下式計算：

2.4抗干擾能力與帶寬比率因子的關系

以載波跟蹤抗干擾品質因數和偽碼跟蹤抗干擾品質因數衡量信號的抗干擾能力。載波跟蹤抗干擾品質因數為

式中，GI0（f），GS0（f）分別表示干擾和信號的功率譜密度函數。

偽碼跟蹤抗干擾品質因數為

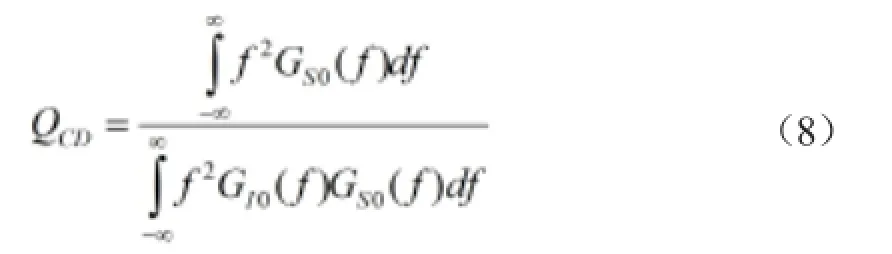
考慮到GS0（f）實際上是帶限的，（7）式、（8）式的積分上限和下限可以改寫為Br/2，-Br/2，即Rcγ，-Rcγ，從而得載波跟蹤抗干擾品質因數、偽碼跟蹤抗干擾品質因數與帶寬比率因子的關系如下

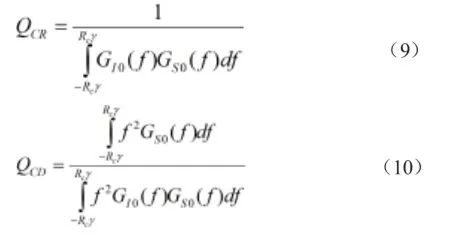
3　帶寬對導航信號性能影響的數值分析

以B P S K（1），B P S K（2），B P S K（10）；BOCs（10，5），BOCs（15，2.5），BOCs（14，2）；BOCc（10，5），BOCc（15，2.5），BOCc（14，2）為對象，分別分析帶寬對BPSK信號、sinBOC信號、cosBOC信號的導航性能的影響。此處BOCs表示sinBOC調制，BOCc表示cosBOC調制。

3.1偽碼跟蹤精度

3.1.1BPSK信號

在0.5≤γ≤1.5的范圍內，BPSK（1），BPSK（2），BPSK（10）的偽碼跟蹤誤差曲線如圖1。

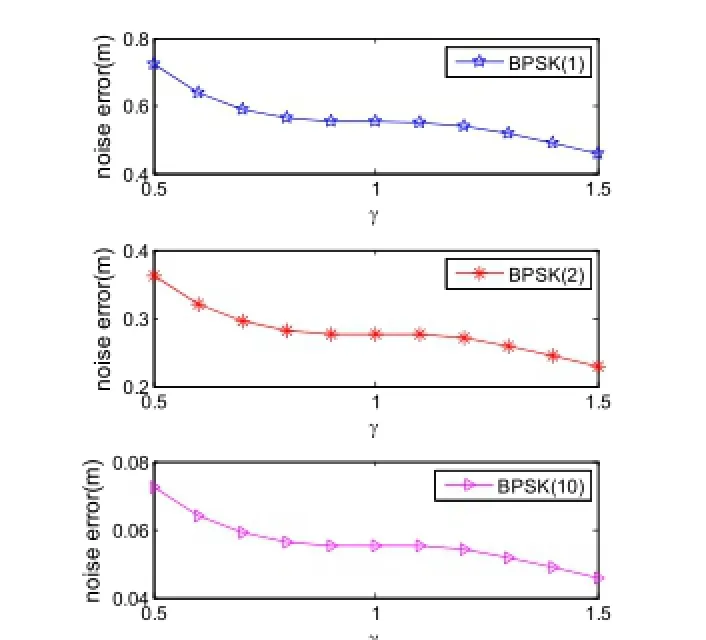
圖1　三種BPSK信號偽距跟蹤誤差曲線

由圖1可見：三種BPSK信號的誤差曲線變化趨勢完全一致；隨著帶寬比率因子增大，BPSK信號偽碼跟蹤誤差變小，即精度升高，升高的幅度整體呈緩慢下降趨勢，且在γ為整數附近持平。

3.1.2BOC信號

定義n=fs/Rc，fs為BOC信號副載波頻率。在n≤γ≤n+1.5的范圍內，六種BOC信號偽碼跟蹤誤差曲線如圖2。

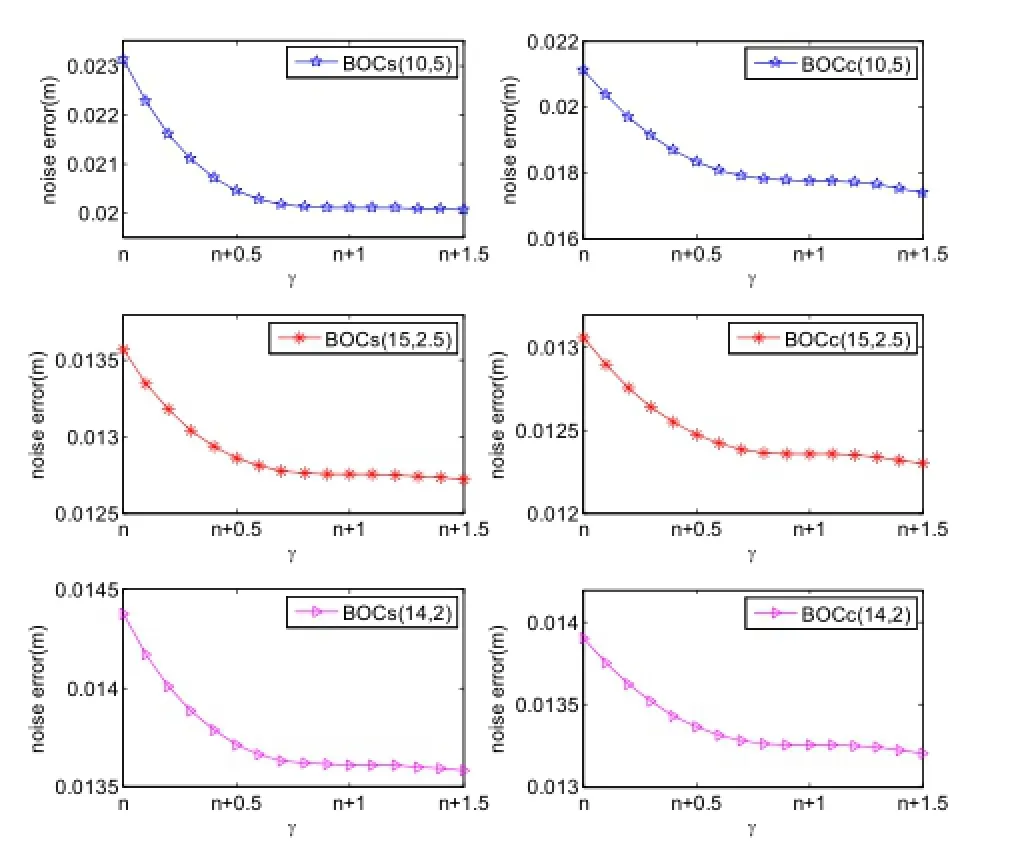
圖2　六種BOC信號偽距跟蹤誤差曲線

由圖2可見：三種sinBOC調制信號的誤差曲線變化趨勢十分相似，隨著帶寬比率因子增大，偽碼跟蹤精度開始逐漸升高，約至γ＞n+0.8后，偽碼跟蹤精度基本持平；三種cosBOC調制信號的曲線變化趨勢十分相似，隨著帶寬比率因子增大，偽碼跟蹤精度開始逐漸升高，約至γ＞n+0.8后，偽碼跟蹤精度升高不明顯。

3.2抗多徑性能

3.2.1BPSK信號

在0.5≤γ≤1.5的范圍內，BPSK（1），BPSK（2），BPSK（10）的多徑誤差曲線如圖3。

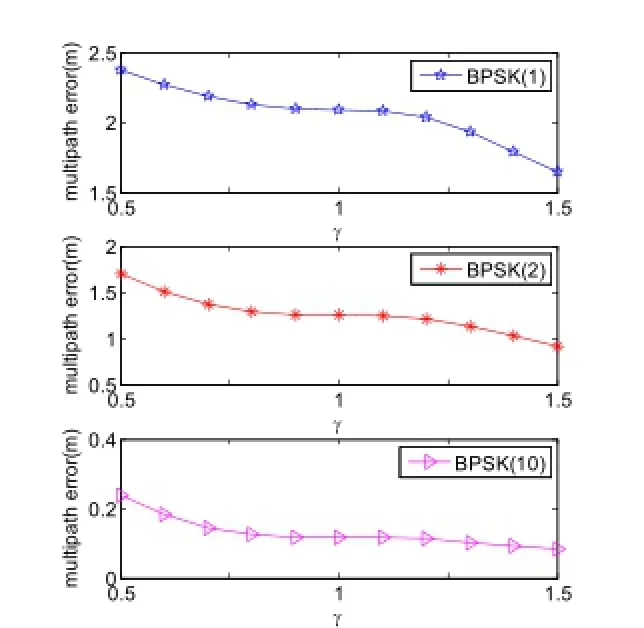
圖3　三種BPSK信號多徑誤差曲線

由圖3可見：三種BPSK信號的誤差曲線變化趨勢完全一致；隨著帶寬比率因子增大，BPSK信號多徑誤差減小，減小的幅度整體呈緩慢下降趨勢，且在 為整數附近持平。

3.2.2BOC信號

在n≤γ≤n+1.5的范圍內，六種BOC信號偽碼多徑誤差曲線如圖4。

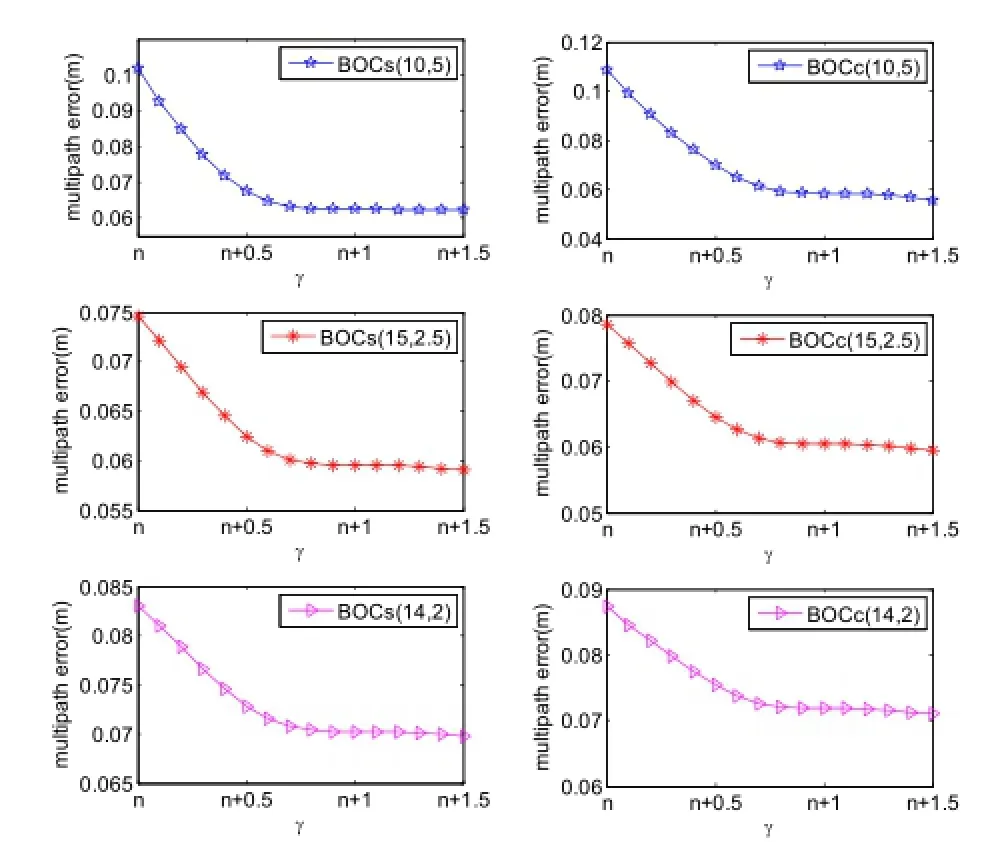
圖4　六種BOC信號多徑誤差曲線

由圖4可見：三種sinBOC調制信號的曲線變化趨勢十分相似，隨著帶寬比率因子增大，多徑誤差開始逐漸降低，約至γ＞n+0.8后，多徑誤差基本持平；三種cosBOC調制信號的曲線變化趨勢十分相似，隨著帶寬比率因子增大，多徑誤差開始逐漸降低，約至γ＞n+0.8后，多徑誤差降低不明顯。

3.3抗干擾能力

3.3.1BPSK信號

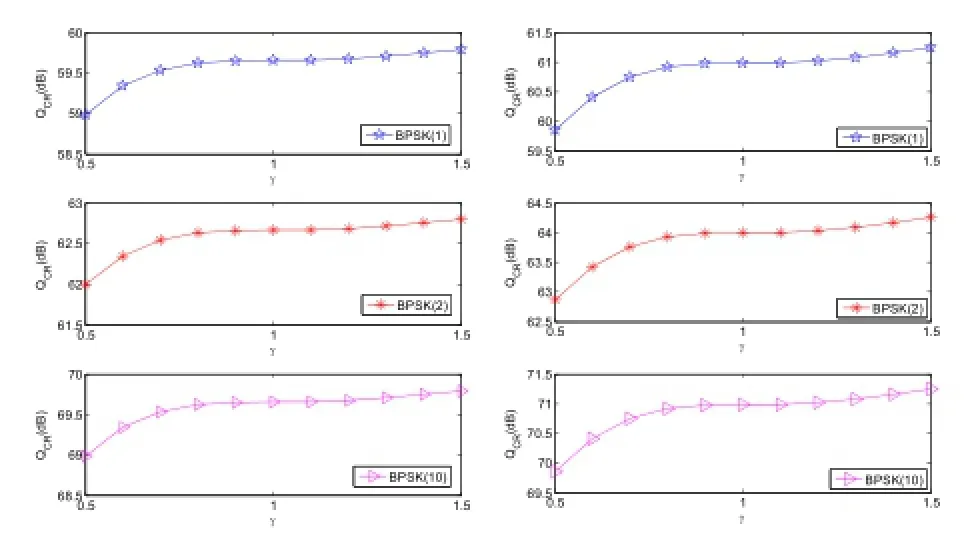
圖5　三種BPSK信號載波跟蹤抗干擾曲線（左：單載波干擾，右：匹配譜干擾）

在0.5≤γ≤1.5的范圍內，BPSK（1），BPSK（2），BPSK（10）的載波跟蹤抗單載波干擾品質因數、載波跟蹤抗匹配譜干擾品質因數曲線如圖5。

由圖5可見：三種BPSK信號的變化趨勢完全一致；隨著帶寬比率因子增大，BPSK信號的載波跟蹤抗干擾品質因數升高，升高的幅度整體呈緩慢下降趨勢，且在 為整數附近持平。

在0.5≤γ≤1.5的范圍內，BPSK（1），BPSK（2），BPSK（10）的偽碼跟蹤抗匹配譜干擾品質因數、偽碼跟蹤抗單載波干擾品質因數的曲線如圖6。

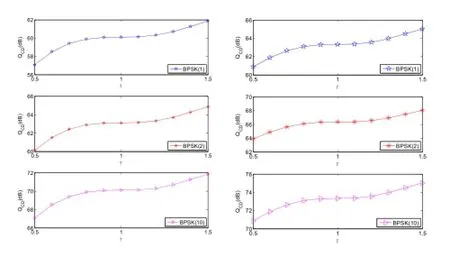
圖6　三種BPSK信號偽碼跟蹤抗干擾曲線（左：單載波干擾，右：匹配譜干擾）

由圖6可見：BPSK信號偽碼跟蹤抗干擾能力與帶寬比率因子關系的結論同圖5結論。

3.3.2BOC信號

在n≤γ≤n+1.5的范圍內，六種BOC信號載波跟蹤抗匹配譜干擾品質因數、載波跟蹤抗單載波干擾品質因數曲線如圖7。

圖7　六種BOC信號載波跟蹤抗干擾品質因數（SC：單載波，MS：匹配譜）

由圖7可見：三種sinBOC調制信號的曲線變化趨勢十分相似，隨著帶寬比率因子增大，載波跟蹤抗干擾品質因數開始逐漸升高，約至γ＞n+0.8后基本持平；三種cosBOC調制信號的曲線變化趨勢十分相似，隨著帶寬比率因子增大，載波跟蹤抗干擾品質因數開始逐漸升高，約至γ＞n+0.8后升高不明顯。

在n≤γ≤n+1.5的范圍內，六種BOC信號的偽碼跟蹤抗匹配譜干擾品質因數、偽碼跟蹤抗單載波干擾品質因數曲線見圖8。由圖8可見：BOC信號偽碼跟蹤抗干擾能力與帶寬比率因子關系的結論同圖7結論。

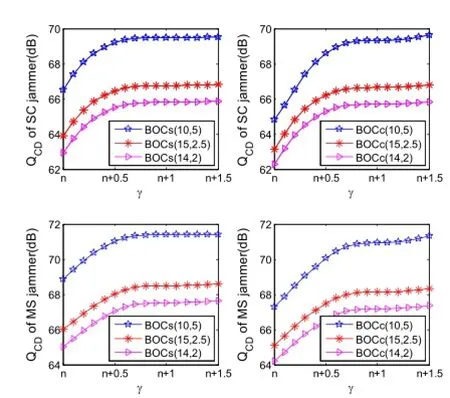
圖8　六種BOC信號偽碼跟蹤抗干擾品質因數（SC：單載波，MS：匹配譜）

4　結果分析

4.1BPSK信號

由上述數值計算的結果可見，不同BPSK調制信號的偽碼跟蹤精度、多徑誤差包絡期望、抗干擾載波跟蹤品質因數和偽碼跟蹤品質因數的變化曲線驚人相似。這種變化規律包括與偽碼速率關系、隨帶寬比例因子的變化趨勢兩個方面。

（1）與偽碼速率的關系

由前述數值計算的結果可見，BPSK信號偽碼跟蹤精度隨帶寬比例因子的變化關系與偽碼速率無關。這可以通過理論分析如下：不同帶寬比例因子的偽碼跟蹤精度區別取決于（3）式中的積分表達式。當偽碼速率由Rc變為R'c=Rc/m時，根據BPSK信號的功率譜密度函數有

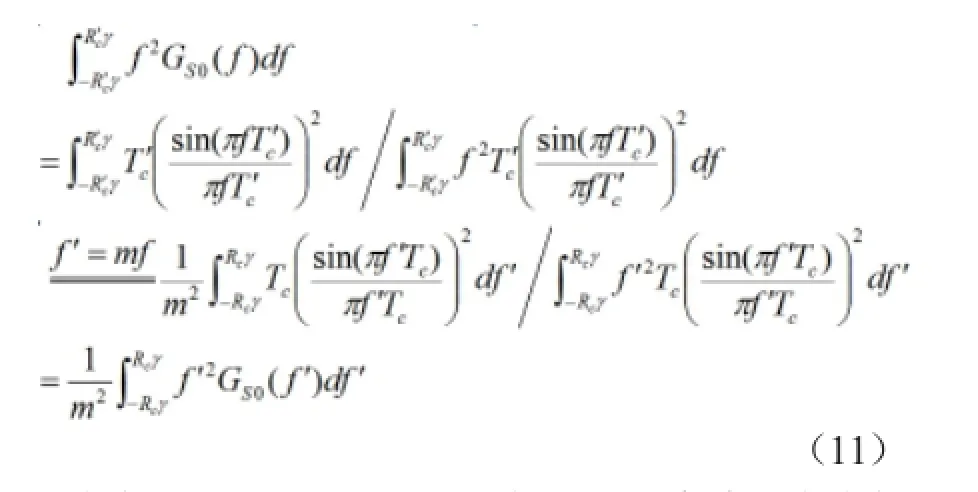
式中，T'c=1/R'c，Tc=1/Rc表示碼元寬度，該式代入（3）式可得，相同的帶寬比率因子條件下，偽碼跟蹤精度與偽碼碼元寬度成正比。這就解釋了圖1中不同偽碼速率條件下偽碼跟蹤精度曲線形狀完全一致，只是縱坐標尺度不同這一現象的原因。

同理，可分析得BPSK調制信號抗多徑性能、抗干擾能力與偽碼跟蹤精度一樣，均與偽碼速率呈線性增長關系。

（2）隨帶寬比例因子的變化趨勢

在上文所述的計算范圍0.5≤γ≤1.5內則有：當γ∈［0.5，0.8］∪［1.2，1.5］，BPSK信號偽碼跟蹤精度、抗多徑性能、抗干擾能力均隨γ增大而增大。當γ∈（0.8，1.2），BPSK信號偽碼跟蹤精度、抗多徑性能、抗干擾能力均隨γ增大幾乎不變。

擴大γ范圍之后，重復上文所述計算過程，有當γ∈［N+0.5，N+0.8］∪［N+1.2，N+1.5］，N=1，2，…，BPSK信號偽碼跟蹤精度、抗多徑性能、抗干擾能力均隨γ增大而增大。當γ∈（N+0.8，N +1.2），BPSK信號偽碼跟蹤精度、抗多徑性能、抗干擾能力均隨γ增大幾乎不變。

綜上所述，BPSK信號帶寬比例因子有多個優化值，γ=M+0.8，M=0，1，2。但是γ=0.8時信號帶寬小，具有所占據頻譜資源最少，與其他信號重疊概率更低因而兼容性更好，更便于發射機和接收機實現等優點。因此，γ=0.8是最優的帶寬比例因子設計值。

4.2BOC信號

由上文所述數值計算的結果可見，不同參數sinBOC，cosBOC信號的偽碼跟蹤精度、多徑誤差包絡期望、抗干擾偽碼跟蹤品質因數和載波跟蹤品質因數的變化曲線驚人相似。這種變化規律包括與偽碼速率關系和n的關系、隨帶寬比例因子的變化趨勢三個方面。

（1）與偽碼速率的關系

首先假設n不變，分析偽碼速率的影響。當偽碼速率由Rc變為R'c=Rc/m時，根據sinBOC信號的功率譜密度函數，采用與（11）式相同的變換，可得偽碼跟蹤精度與偽碼碼元寬度成正比。同理，cosBOC信號也是如此。這表明，偽碼速率不會影響BOC調制信號偽碼跟蹤精度曲線的形狀，同樣對于抗多徑和抗干擾性能亦是如此。

（2）與n的關系

觀察前述三種sinBOC信號、三種cosBOC信號的性能曲線可見，n值不同曲線形狀不同。可見，BOC調制信號偽碼跟蹤精度曲線隨帶寬比率因子的變化與n有關。

（3）隨帶寬比例因子的變化趨勢

在前文所述計算范圍n≤γ≤n+1.5內有：當γ∈［n，n+0.8］，sinBOC信號、cosBOC信號的偽碼跟蹤精度、抗多徑性能、抗干擾能力均隨帶寬增大而增大。當γ∈（n+0.8，n+1.5］，sinBOC信號、cosBOC信號的偽碼跟蹤精度、抗多徑性能、抗干擾能力均隨γ增大幾乎不變。

擴大γ的范圍，重復前文所述的計算過程，則有γ∈（n +1.5，∞），sinBOC信號的偽碼跟蹤精度、抗多徑性能、抗干擾能力均隨γ增大變化幾乎不變；cosBOC信號的偽碼跟蹤精度、抗多徑性能、抗干擾能力均隨γ增大變化在部分區間幾乎不變，另一部分區間增長不明顯。

綜上，sinBOC信號最優化的帶寬比例因子是γ=n+0.8，n=fs/Rc。cosBOC信號γ=n+0.8是局部性能優化值，當γ增大時在部分區間cosBOC信號可能獲得略好的性能，但差別不明顯，因此考慮頻率資源利用率和實現代價對于cosBOC信號γ=n+0.8也是最優的帶寬比例因子設計值。

5　結束語

本文引入帶寬比例因子這一參量，以偽碼跟蹤精度、抗多徑性能、抗干擾性能優化為目標，對BPSK信號、sinBOC，cosBOC信號的帶寬進行了優化設計。數值計算與理論分析結果表明，增大帶寬不一定能夠帶來性能的提升；BPSK信號最優化的帶寬設計對應于γ=0.8，即主瓣寬度的0.8倍；sinBOC，cosBOC信號最優化的帶寬設計對應于γ=n+0.8，即信號帶寬為±（fs+0.8Rc）。此優化設計節約了頻率資源，提高了現有頻率的利用效率，并應用于工程實際。

［1］Isidre Mateu， Cyrille Boulanger， Jean-Luc Issler， etc. Exploration of Possible GNSS Signals in S-band. 22nd International Meeting of the Satellite Division of the Institute of Navigation， Savannah， GA， September 22-25， 2009: 1573-1587

［2］F. Soualle， T. Bey， J-J. Floch， etc. Assessment on the Use of S-Band for Combined Navigation and Communication. 24th International Technical Meeting of the Satellite Division of the Institute of Navigation， Portland OR， September 19-23， 2011: 1219-1233

［3］Zheng Yao， Mingquan Lu. Optimized Modulation for Compass B1-C Signal with Multiple Processing Modes. 24th International Technical Meeting of the Satellite Division of the Institute of Navigation， Portland OR， September 19-23， 2011: 1234-1242

［4］Feng Xu. A Complexity Reduced Frequency Domain Receiver for Galileo and GPS L1 Signals. 22nd International Meeting of the Satellite Division of the Institute of Navigation， Savannah， GA， September 22-25， 2009: 3198-3208

［5］Stefan Erker， Steffen Th?lert， Johann Furthner， etc. GPS L5 “Light′s on！” - A First Comprehensive Signal Verification and Performance Analysis. 22nd International Meeting of the Satellite Division of the Institute of Navigation， Savannah， GA， September 22-25， 2009: 1544-1551

［6］俞盈帆譯.增強系統設計與性能.GNSS2-P2-GS-201， TN3.8， 2001: 78

［7］Irsigler Markus， Rodriguez J A A， Hein G W. Criteria for GNSS Multipath Performance Assess- ment［C］. ION GNSS 2005， Virginia， 2005: 2166-2177

［8］Gunter W Hein， Jose-Angel Avila-Rodriguez. Combined Galileo PRS and GPS M code［J］. Inside GNSS， 2006（1）:48-55

［9］李春霞，楚恒林，王宏兵.BOC調制信號抗干擾能力分析.測繪科學技術學報，2012，29（6）:414-417

Optimized Bandwidth of the Navigation Signal

Ma Xu， Li Chunxia
（Beijing Satellite Navigation Center， Beijing， 100094）

The navigation signal frequency bandwidth increasingly becomes important recourse strived by the satellite navigation system builders， and optimized bandwidth design of the navigation signal is good for improving frequency use effciency and multi-system compatibility. In this paper， the new parameter of bandwidth ratio index is proposed， and taken the example of the BPSK， sinBOC and cosBOC signals， the variations of pseudo noise （PN） code tracking precision， multipath mitigation capability， anti-jamming capability with the bandwidth ratio index are analyzed，and the bandwidth ratio index is optimized aiming at these performances' optimization. The results show that the optimized BPSK signal's bandwidth is 0.8Rc， the optimized sinBOC and cosBOC signal's bandwidth is ±（fs+0.8Rc）.

bandwidth； tracking precision； multipath； anti-jamming

10.3969/j.issn.1672-7274.2015.02.002

TN96文獻標示碼：A

1672-7274（2015）02-0007-06

馬煦，碩士，高級工程師，長期從事衛星導航基準站研究。

李春霞，博士，高級工程師，長期從事衛星導航技術研究。