基于小波閥值法去白噪聲的方法研究

丁同嶺，王成江

(三峽大學電氣與新能源學院，湖北 宜昌 443002)

1 引言

隨著科學技術的發(fā)展，信號的處理成了科學研究中的不可或缺的一部分，近些年，除了傳統(tǒng)的傅里葉變換外，小波分析也在信號處理中到了很廣泛的應用。對于其性質(zhì)隨時間穩(wěn)定不變的信號，處理的理想工具仍然是傅立葉分析。但是在實際應用中的絕大多數(shù)信號是非穩(wěn)定的，而特別適用于非穩(wěn)定信號的工具就是小波分析。在信號的采集過程中不可避免的含有噪聲，其中就包括白噪聲，噪聲嚴重地影響對實驗結(jié)果的分析，必須把數(shù)據(jù)進行預處理，盡可能的消除噪聲的干擾。小波分析是在傅立葉分析的基礎上發(fā)展起來的，它既保持了傅立葉分析的優(yōu)點，又彌補了傅立葉分析的不足。與傅立葉分析相比，小波分析具有多分辨率的特點，它較好地解決了時域和頻域分辨率的矛盾，巧妙地利用了非均勻分布的分辨率，在低頻段用較高的頻率分辨率和較低的時間分辨率，而在高頻段則采用較低的頻率分辨率和較高的時間分辨率。因此利用小波變換時頻域的局部化性質(zhì)可以很好地獲得信號的局部化特性，對突變信號和非平穩(wěn)信號的檢測非常有效。研究表明，利用小波分析能有效地消除白噪聲。

2 Fourier分析方法

對很多信號來說，傅立葉分析能給出信號中包含的各種頻率成分。Fourier分析在信號分析處理中起著非常重要的作用，這是因為Fourier分析能將信號的時域特性變換為頻域特性。分析時域信號f(t)，總是假定其能量有限，但Fourier分析有一定的局限性，用傅立葉變換提取信號的頻譜需要利用信號的全部時域信息，傅立葉變換沒有反映出隨著時間的變化信號頻率成分的變化情況，傅立葉變換的積分作用平滑了非平穩(wěn)信號的突變成分。

3 短時Fourier變換

假設f(t)為能量有限信號，則以g(t)作為窗函數(shù)的窗口傅立葉變換定義:

窗口傅立葉變換的物理意義:

若g(t)的有效窗口寬度為Dt，則WFg(w，b)給出的是f(t)在局部時間范圍[b－Dt/2，b+Dt/2]內(nèi)的頻譜信息。有效窗口寬度Dt越小，對信號的時間定位能力越強。

假設 f(t)的傅里葉變換為 F(η)，gw，b(t)的傅里葉變換為 Gw，b(η)，則:

這是窗口傅里葉變換的頻域表示形式，窗口傅里葉頻域變換的物理意義為若G(η)的有效窗口寬度為Dω，則WFg(ω，b)給出的是F(η)在局部頻率范圍[ω－Dω/2，ω+Dω/2]內(nèi)的頻譜信息。有效窗口寬度Dω越小，對信號的頻率定位能力越強。由不確定性原理可知，窗口傅立葉變換的時間分辨率和頻率分辨率不可能同時提高，只能以一種分辨率的降低來換取另一種分辨率的提高。

4 小波變換

由于傅里葉分析方法和窗口傅里葉分析方法的局限性，小波變換得以產(chǎn)生和發(fā)展[1－5]，小波變換分為連續(xù)小波變換，離散參數(shù)小波變換和離散小波變換，其主要區(qū)別在于時間和控制窗口是否離散化。連續(xù)小波變換一般表示形式為:

其時域上的物理意義經(jīng)常被稱為數(shù)學顯微鏡的作用，即一組有效寬度的不同窗口的Fourier變換的匯集。在頻域上，若 f(t)的傅立葉變換為 F(w)，ψa，b的傅立葉變換為 ψa，b，則根據(jù) Parseval定理，有:

另外，對于連續(xù)小波變換，其時域窗口寬度和頻域窗口寬度的乘積為一個定值，這也被稱為恒Q性質(zhì)，也是小波變換區(qū)別于其他變換的重要特征，其示意圖如圖1所示。

圖1 A取不同值時小波變換對信號分析的時－頻區(qū)間

為了保證小波變換的逆變換存在，連續(xù)小波變換的母小波必須滿足容許條件[6]

為了便于計算機進行計算，通過對時移參數(shù)和窗口寬度參數(shù)的離散化，我們得到了離散參數(shù)小波變換和離散小波變換，此處我們主要利用了離散小波變換來對信號進行去噪的。小波在離散的過程中仍應滿足連續(xù)小波變換中的容許條件。小波函數(shù)的選擇與離散化的程度有關系，離散化參數(shù)取樣間隔很小時對小波函數(shù)的限制也小，而離散化參數(shù)的取樣間隔很大是對小波函數(shù)的限制也會很大。由多變率分析和Mallat算法并借助于MATLAB我們可以迅速得到分解并改造函數(shù)的一種方法。

近年來，小波理論得到了非常迅速的發(fā)展，而且由于其具備良好的時頻特性，因而實際應用也非常廣泛。在去噪領域中，小波理論也同樣受到了許多學者的重視，他們應用小波進行去噪并獲得了非常好的效果。具體來說小波去噪方法的成功主要得益于小波變換具有如下特點[7]:

(1)低熵性，小波系數(shù)的稀疏分布，使得圖象變換后的熵降低;

(2)多分辨率，由于采用了多分辨率的方法，所以可以非常好地刻畫信號的非平穩(wěn)特征，如邊緣、尖峰、斷點等;

(3)去相關性，因為小波變換可以對信號進行去相關，且噪聲在變換后有白化趨勢，所以小波域比時域更利于去噪;

(4)選基靈活性，由于小波變換可以靈活選擇變換基，從而對不同應用場合，對不同的研究對象，可以選用不同的小波母函數(shù)，以獲得最佳的效果。

4.1 小波去噪模型的建立

為了更好的對比利用小波分解去除白噪聲前后的效果，選取利用MATLAB編程語言生成了幅值不同的方波信號作為此次研究的原始信號，然后加入噪聲強度已知的白噪聲作為干擾信號，通過小波分解的方法來盡可能的去除加入的白噪聲。小波分解通常通過以下幾個步驟來完成[8]:

(1)對已有的信號進行小波分解

(2)合理的確定小波各層細節(jié)的閥值，來對得到的小波分解系數(shù)進行閥值處理。

(3)通過小波逆變換對信號進行重構(gòu)。

小波去噪的效果主要取決于小波分解的層數(shù)是否合適與小波各層細節(jié)閥值的確定是否合適。

4.2 小波層數(shù)的選擇

小波層數(shù)的選擇沒有固定的公式，一般根據(jù)經(jīng)驗嘗試獲取，在一般情況下，隨著分解層數(shù)的增多，信號細節(jié)丟失越多，分解層數(shù)太少，對信號的信息獲取又太少。此處取的信號分解層數(shù)為3層或4層。

4.3 小波系數(shù)閥值的選取

(1)無偏估計原則:是一種基于 Stein無偏似然估計原理的自適應閾值選擇。對于給定的閾值T，得到它的似然估計，再將似然T最小化，就得到了所選的閾值，這是一種軟件閾值估計。

(2)閥值原則:固定閾值T的計算公式:

其中，n是信號的長度。

(3)啟發(fā)式閥值原則:是無偏似然估計和固定閾值估計原則的折中。如果信噪比很小，按無偏似然估計原則處理的信號噪聲較大，在這種情況下，就采用固定閾值形式。

(4)極值閥值原則:采用極大極小值原理選擇閾值，它產(chǎn)生一個最小均方誤差的極值，而不是沒有誤差。統(tǒng)計學上，這種極值原理用來設計估計器。因為被消噪的信號可以看作與未知回歸函數(shù)的估計器相似，這種極值估計器可在給定的函數(shù)中實現(xiàn)最大均方誤差最小化。

4.4 軟閥值和硬閥值

在確定閾值后，可以采用硬閾值或軟閾值的處理方法對小波系數(shù)做閾值處理。硬閾值法只保留大于閾值的小波系數(shù)并將其他的小波系數(shù)置零，其表達式如下:

軟閾值法將小于閾值的小波系數(shù)置零，并把大于閾值的小波系數(shù)向零做收縮，其表達式如下:

硬閾值信號和軟閾值信號見圖2。

圖2 硬閥值與軟閥值

從圖中可以看出，硬閾值方法能夠保留更多真實信號中的尖峰特征，但在某些點上會產(chǎn)生間斷，而軟閾值方法是在硬閾值的基礎上將邊界出現(xiàn)的不連續(xù)點收斂到零，這樣可有效避免間斷，使得重建的信號比較光滑。

5 小波去噪的MATLAB仿真對比

原始信號與加完白噪聲之后的比較如圖3。

下圖顯示的分別是噪聲信號進行小波分解后產(chǎn)生的近似系數(shù)和四個細節(jié)系數(shù)的波形圖，通過近似系數(shù)和細節(jié)系數(shù)可以得到小波系數(shù)，對小波系數(shù)進行重構(gòu)后得到對原信號的還原，這里不對細節(jié)系數(shù)進行任何修改。

圖3 噪聲加入前后信號的比較

圖4 小波近似系數(shù)與細節(jié)系數(shù)

通過軟閥值法對信號處理前后的對比如圖如圖5:

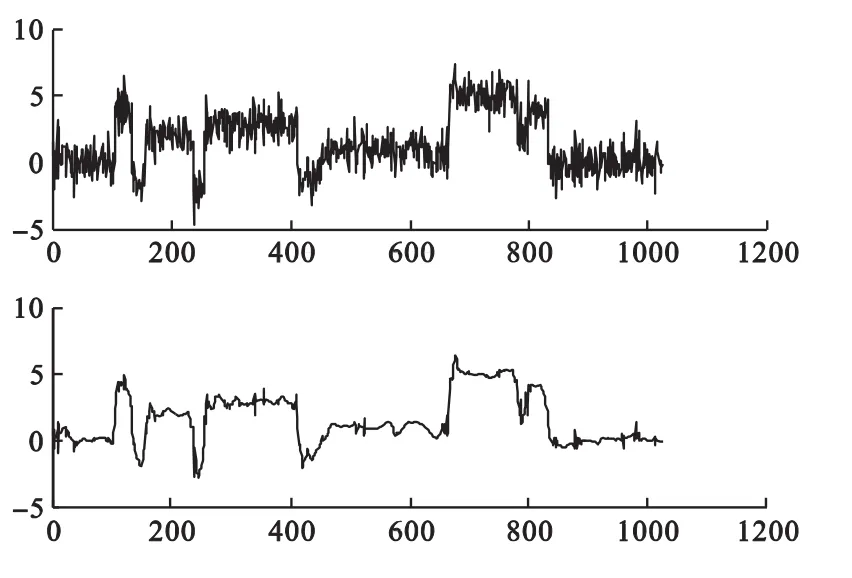
圖5 軟閥值法處理前后信號的對比圖

圖6 硬閥值處理前后信號的對比圖

通過硬閥值處理前后噪聲信號的對比如圖6:

通過硬閥值和軟閥值處理的效果圖可以看出，硬閥值去噪和軟閥值去噪均能濾除大部分噪聲成分，但不能完全濾除，硬閥值去噪和軟閥值去噪的效果有所不同，經(jīng)過硬閥值處理得到的信號比較粗糙，但很好的保留了信號尖峰部分，而軟閥值處理則平滑了尖峰部分，使信號整體看起來比較平滑。

6 總結(jié)

通過運用小波變換來去除白噪聲，對傅里葉、短時傅里葉、小波變換對比總結(jié)如下:

6.1 傅里葉變換

(1)首先傅里葉變換是周期函數(shù)的傅里葉級數(shù)展開過程中周期由定值向無窮大變化的一個過程。

(2)傅里葉級數(shù)中各項系數(shù)例如cosx項系數(shù)是原函數(shù)與其在某一定義域內(nèi)的積分，我們可以將該過程理解為對這兩個函數(shù)進行相關，將相關系數(shù)作為該頻率處的強度。

(3)經(jīng)過傅里葉變換之后得到的是頻域的信息，時間信息完全丟失，但可以通過逆變換完全恢復原始信號。傅里葉逆變換同樣可以理解為相關，只是此時需保證變換時t不變，也就是計算某時刻不同頻率波形與傅里葉變換之后的頻域信號之間的相關，積分后得到該時刻各頻率分量在該時刻的總貢獻。

(4)從泛函的角度，我們可以把傅里葉級數(shù)中的三角函數(shù)看做一個線性函數(shù)空間的一個基，這里與線性代數(shù)里的線性空間有兩點不同，第一該處是函數(shù)空間，每個元素都是一個函數(shù)而不是一個數(shù)，第二這里是無限維空間，基有無限多個元素。

(5)傅里葉變換把信號的時域特征和頻域特征聯(lián)系在了一起，使我們可以從信號的時域和頻域兩個角度觀察和分析信號，但二者卻又是絕對分離的即在頻域不包含任何時域信息，在時域同樣找不到任何頻域信息，對于傅里葉頻譜中的某一頻率，無法知道這一頻率是何時產(chǎn)生的，只能從全局上分析信號。這樣在信號分析中就面臨著時域和頻域的局部化的矛盾。

6.2 短時傅里葉變換

由上敘述可知傅里葉變換之后的圖像僅包含頻域信息，丟失了時域信息，在那些同時需要頻域和時域信息的時候(在什么時候存在哪些頻率)就顯得無能為力，因此出現(xiàn)了短時傅里葉變換，短時傅里葉變換認為在一個小的窗函數(shù)時間段內(nèi)信號是穩(wěn)定的，信號包含的頻率是不變的，利用一個窗口函數(shù)與原始函數(shù)卷積，在特定的時間僅計算該時間前后窗函數(shù)時間內(nèi)的信號的傅里葉變換作為該時間點的傅里葉變換，即該時刻的頻譜。

6.3 小波變換

而寬的窗口函數(shù)頻率分辨率高但時間分辨率低，低頻信號時間分辨率較低而頻率分辨率較高，這是由海森堡不確定原理所確定的。這樣便產(chǎn)生了小波，小波可以理解為是在短時傅里葉變換的基礎上對窗口函數(shù)增加了一個尺度因子，該尺度因子伴隨著頻度變換而變化，使得在低頻時降低窗口寬度增加時間分辨率而在高頻時增加窗口寬度增加頻率分辨率。而小波變換就不一樣了，具有多尺度特性，可以把頻率強度和位置時刻聯(lián)系起來，一定程度上解決了傅里葉分析的缺點，但這并不是說小波分析方法可以替代傅里葉和短時傅里葉分析方法。如果是單純進行頻率域上面的分析，就沒有必要使用小波分析的方法，使用傅里葉方法更簡單，效果也更好一些。小波變換在使用過程中還用很多不確定性的問題，比如傅里葉變換的基函數(shù)是確定的，就是正弦和余弦函數(shù)，而小波變換的基函數(shù)則是可構(gòu)造的。這種不確定性就帶來了選擇基函數(shù)的困難性，需要根據(jù)經(jīng)驗和嘗試才能找到合適的基函數(shù)。還有文中提到的小波分解層數(shù)，小波閥值選取等等都具有不確定性，小波變換應用的難點便在于如何確定這些不確定性參數(shù)。

[1]Zhang Q，et al.Wavelet network[J].IEEE Trans Neural Networks，1992，3(6):889 －898.

[2]Bahavik R，et al.Wave-net:a multiresolution，hierarchical neural network with localized learning[J].AIChE Journal，1993，39(1):57 －81.

[3]Zhang J，et al.Wavelet neural network for function learning[J].IEEE Transactions on Signal Processing，1995，43(6):1485 －1497.

[4]Zhang Q.Using wavelet network in nonparametric estimation[J].IEEE Transactions on Neural Networks，1997，8(2):227 －236.

[5]王成江，聶德鑫.放電聲發(fā)射波檢測中小波基的選擇[J]高電壓技術，2003，29(10):39 －42.

[6]姚天任.現(xiàn)代數(shù)字信號處理[M].華中科技大學出版社，1999.

[7]孫延奎.小波分析及其應用[M].北京:機械工業(yè)出版社，2005.

[8]Berkner K，Wells Jr R O.Wavelet transforms and denoising algorithm[C].//Signal，System ＆ Computers，Conference Record of the Thirty-Second Asilomar Conference，1998:1639 －1643.