平面鉸鏈四桿機構的軌跡綜合方法

于紅英，趙彥微，許棟銘

(哈爾濱工業大學 機電工程學院，150001哈爾濱)

軌跡綜合是平面連桿機構綜合的3類基本問題之一，其主要目的是找到一個連桿機構，使其連桿平面上某一點能依次通過某一預先給定的軌跡.平面鉸鏈四桿機構的軌跡綜合一般有3種方法:圖解法、解析法和圖譜法.

傳統的圖解法存在作圖誤差大，綜合精度低等缺點，目前已經很少使用.解析法通常與各種優化方法結合運用，通過尋求最小目標函數來獲得最優解［1-4］，求解精度較高，但通常要受到初值選擇以及尋優方法的影響而難于收斂.隨著計算機技術的發展，計算機的海量存儲能力和快速檢索能力使得圖譜法在軌跡綜合中應用得越來越廣泛.文獻［5］通過建立已知機構的連桿轉角曲線數據庫，將要實現的封閉軌跡曲線也轉化成連桿轉角曲線，再與數據庫中已有轉角曲線比較，進而獲得滿足要求的機構.文獻［6-7］中提出利用神經網絡對平面連桿機構進行軌跡綜合，通過運動學仿真建立了一個大樣本庫，然后對神經網絡進行訓練，可以通過訓練好的神經網絡找到綜合問題的近似解.文獻［8-9］中采用小波分析方法提取連桿軌跡的特征參數，構建連桿曲線圖譜庫進行軌跡綜合.文獻［10］中采用均勻B樣條曲線來擬合連桿軌跡，提取B樣條曲線控制頂點的坐標作為軌跡特征參數進行軌跡綜合.文獻［11］中將連桿曲線進行快速傅里葉變換，提取傅里葉級數作為描述連桿曲線的諧波特征參數，然后生成連桿曲線的電子圖譜庫，再從庫中檢索出滿足要求的機構.上述各種方法中有些方法圖譜庫中存儲數據較多，有些方法需要進行復雜后處理才能得到機構的實際尺寸和安裝尺寸，導致不易用編程的方法快速找到合適的機構.

本文以曲柄搖桿機構為例，采用三次非均勻B樣條曲線來擬合平面連桿曲線，通過程序自動獲取連桿曲線的型值點進行B樣條曲線擬合，將B樣條曲線的控制多邊形各相鄰兩邊間的夾角作為表征連桿曲線形狀特征的參數，連同對應的機構尺寸參數建立連桿曲線的電子圖譜庫，再利用人工神經網絡進行特征參數匹配，快速獲得合適的平面鉸鏈四桿機構，最終達到軌跡綜合的目的.

1 原始連桿曲線的生成

如圖1為曲柄搖桿機構ABCD，其中假設AB為曲柄，各桿實際桿長為l1、l2、l3、l4和l5，BP與連桿BC沿逆時針方向所成的角為δ(0°≤δ＜360°)．

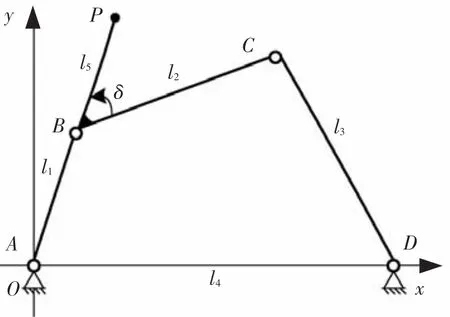
圖1 曲柄搖桿機構的參數

為研究方便，本文采用量綱一的相對桿長，即取曲柄r1=l1/l1=1，r2=l2/l1，r3=l3/l1，r4=l4/l1，r5=l5/l1．眾所周知，只有r1、r2、r3及r4滿足一定的長度關系時，才能構成以r1為曲柄的曲柄搖桿機構．現以r2=a(a≥1)為例說明如何確定r3、r4的取值范圍．如圖2所示，建立以相對桿長r2、r3、r4為坐標軸的三維直角坐標系Or2r3r4．過r2軸上的一點(a，0，0)作一平行于Or3r4的平面M，在平面M內過點(a，1，a)和點(a，a，1)作兩條與r3軸正向成45°的射線EE'和FF'，連接E、F兩點．可以證明，線段EF與兩射線EE'、FF'所圍成的條形區域為r3、r4的取值范圍．如圖2中G點的坐標為(a，b，c)，則代表r1=1，r2=a，r3=b，r4=c的曲柄搖桿機構尺寸型．當r2變化時，r3、r4在條形區域內的值應滿足如下關系:

圖2 曲柄搖桿機構桿長尺寸分布

本文按照一定的步長變化r2、r3、r4的值，編寫程序生成了一定數量的曲柄搖桿機構的尺寸型．對于每一個尺寸型的曲柄搖桿機構，隨連桿點P位置的不同(即r5和δ發生變化)產生的連桿曲線也不同．文獻［12］在連桿平面上取了5行10列共50個點作為連桿點P的50個位置(見圖3)．

圖3 連桿點位置分布

本文為豐富圖譜庫中連桿曲線，選取了11行21列共231個點作為P的231個位置，其坐標值可表示為

根據曲柄搖桿機構的尺寸參數變化，利用計算機可批量完成連桿曲線的數據采集，即每一個尺寸型的曲柄搖桿機構的每一個連桿點在曲柄旋轉一周時所形成的連桿曲線上N個點Qi(i=1，2，3，…，N)的坐標．通過試驗，每條連桿曲線上取N=720時即可代表該曲線．

2 連桿曲線的歸一化

為便于連桿曲線特征匹配，需要對連桿曲線進行歸一化處理，使所有曲線的長、短和放置方式統一，無論待識別的曲線是正放、豎放、斜放，或大或小都能被識別出來.歸一化具體方法如下.

1)曲柄搖桿機構A0B0C0D0P0的起始位置和曲柄沿逆時針旋轉時生成的連桿曲線如圖4(a)所示，找出連桿曲線上相距最遠的兩個點G0、H0．

2)將機構A0B0C0D0P0和連桿曲線平移，使偏左的點G0與坐標原點重合，平移變換公式如式(1)所示:

式中T1為平移變換矩陣，i代表歸一化過程中需要進行坐標變換的各點的標號.變換后機構和連桿曲線如圖4(b)所示.

圖4 連桿曲線歸一化過程

3)如圖4(b)所示，計算G01H01與x軸正向逆時針所成的角α0，將機構A01B01C01D01P01和連桿曲線順時針旋轉α0使G01H01與x軸重合，旋轉變換公式如式(2)所示，變換后機構和連桿曲線如圖4(c)所示.

式中R1為旋轉變換矩陣．

4)如圖4(c)所示，為使曲線凸起部分靠近y軸，找到當前曲線上距x軸最遠的點Ⅰ02，Ⅰ02到x軸的垂足為點J02．計算G02J02和J02H02的長度，若，則將機構A02B02C02D02P02連同連桿曲線繞y軸做反射變換，再平移，使H02與坐標原點重合，變換公式如式(3)所示，變換結果如圖4(d)所示;若，則保持原圖，不進行變換，但交換G02、H02兩點代號，即使H02點位于坐標原點．

式中:S1為反射變換矩陣，T2為平移變換矩陣，且當xⅠ02＞xH02-xⅠ02時，

當xⅠ02≤xH02-xⅠ02時，

5)如圖4(d)所示，為保證曲線凸起部分在x軸的上方較大，需判斷Ⅰ03點縱坐標的正負，然后進行式(4)的變換．若yⅠ03＜0，則繞x軸做反射變換;若yⅠ03≥0，則不變化．變換結果如圖4(e)所示.

式中S2為反射變換矩陣，且當yⅠ03＜0時，

當yⅠ03≥0時，

6)如圖4(e)所示，將機構A04B04C04D04P04連同連桿曲線縮小倍，比例變換公式如式(5)所示，變換結果如圖4(f)所示.

式中S為比例變換矩陣．

機構A0B0C0D0P0連同連桿曲線經過歸一化處理，得到歸一化后的機構A'0B'0C'0D'0P'0和歸一化后的連桿曲線以及在歸一化過程中相關的6個歸一化參數:xG0、yG0、α0、xⅠ02、yⅠ03、k0．歸一化變換矩陣是以上6個變換矩陣的乘積，即

3 連桿曲線型值點的選擇

在使用B樣條曲線對連桿曲線進行擬合時，連桿曲線上型值點的選擇對曲線的特征參數提取及其最終的擬合精度具有重大影響.由于本文利用神經網絡進行曲線特征參數的匹配，而神經網絡的輸入特征參數的數目必須是固定的，連桿曲線又形態各異，初始型值點數目可能并不相等，因此必須設計一套型值點自動選擇算法，從連桿曲線的720個點中找到m個能夠描述曲線特征的點qi(i=0，1，…，m-1)．具體過程如下:

1)通過數值構造的方式計算出連桿曲線上各點的一階導數、二階導數、曲率，選取軌跡上的極值點、拐點以及曲率極值點作為初始型值點，如圖5(a)中“+”所示.

2)刪去步驟1)中較為密集的型值點，遵循刪去曲率較小點的原則，剩余的型值點如圖5(b)中“o”所示.

3)步驟2)中剩余型值點數為s，設最終有m+t個特征參數作為神經網絡的輸入，其中t為連桿曲線精確擬合時再次插入的型值點數．為了保證神經網絡輸入特征參數數目的一致性，應使初始型值點數由s變到m．若s＞m，則將另外的s-m個型值點依次插入到兩個距離最遠的型值點中;若s＜m，則在型值點密集處刪去m-s個點．經過反復試驗，m=12時在型值點數目較小的情況下擬合效果較好，如圖5(c)中“?”所示.

4)對初始型值點進行調整，步驟3)中獲得的初始型值點并不能完全滿足擬合精度的要求.因此必須要對初始型值點進行調整.已知連桿曲線的N個點Qi(i=1，2，3，…，N)，結合下文中的B樣條曲線擬合方法，由m個初始型值點得到初始擬合曲線上的N個點Wi(i=1，2，3，…，N)．為了便于度量擬合質量，定義最大擬合誤差esmax=max(‖Qi-Wi‖)(i=1，2，3，…，N)、平均擬合誤差，其中‖Qi-Wi‖表示點Qi到點Wi的距離．最大擬合誤差反應了擬合曲線和連桿曲線最大分離程度，而平均擬合誤差則反應了整體的擬合效果．規定esmax＜0.010和es＜0.008時滿足初始擬合精度要求．分別檢查esmax和es，若滿足要求則可以不再調整型值點，若達不到要求，則找到連桿曲線上出現最大擬合誤差點的曲線段的兩個型值點，按照一定步長調整左右型值點位置，重新擬合曲線．重復以上步驟，保證型值點數目不變情況下調整型值點的位置，使擬合誤差滿足預期的精度要求，得到m個型值點qi(i=0，1，…m-1)．最終得到的型值點如圖5(d)中“*”所示．

圖5 初始型值點選擇的過程

4 曲線特征提取與圖譜庫建立

給定連桿軌跡曲線(通常都是封閉的曲線)上的一組首尾重合的數據點，可構造出一條通過該組數據點且滿足誤差要求的Ck-1連續(具有k-1階參數連續性)的k次封閉的B樣條插值曲線［13-15］．本文采用具有二階參數連續性的三次非均勻B樣條閉合的插值曲線對連桿曲線上的數據點進行擬合，將提取的型值點qi(i=0，1，…，m-1)作為已知的數據點，擬合的B樣條曲線由n+1個控制頂 點di(i=0，1，…，n)與 節 點 矢 量U=［u0，u1，…，un+k+1］來定義．

首先，要確定節點矢量U．本文對于封閉的三次非 均 勻B樣 條曲線定義域［uk，un+1］=［u3，un+1］=［0，1］內的節點采用規范積累弦長參數化法來確定，該方法能夠如實反映數據點按弦長的分布情況，定義域外節點確定為u0=un-2-1，u1=un-1-1，u2=un-1，un+2=1+u4，un+3=1+u5，un+4=1+u6．

對于閉合的連桿曲線，B樣條曲線的首末端點連接處同樣要求具有C2連續性，令首末3個控制頂點依次相重合d0=dn-2，d1=dn-1，d2=dn，故未知控制頂點共有n-2個．對于插值曲線，反算過程中應使曲線的分段連接點依次與B樣條曲線定義域內節點一一對應起來，則

用于擬合m+1個數據點qi(i=0，1，…，m)的三次B樣條插值曲線方程為

將曲線定義域內的節點值代入式(6)應滿足插值條件，即

式(7)中含有m+1=n-1個方程，對于C2連續的三次非均勻B樣條閉合曲線，由于首末數據點相重合q0=qm，則方程數目減少一個，剩m=n-2個．至此可由m=n-2個方程構成的方程組解出n-2個未知控制頂點．根據以上條件整理可得到以下矩陣方程:

其中

解矩陣方程即可求出未知的控制頂點，至此可得到全部控制頂點.由反算出的控制頂點通過德布爾算法［13］即可求得B樣條曲線上的點.

已知連桿曲線的m個初始型值點，首先利用上述方法得到初始的擬合曲線上的N個點Wi(i=1，2，3，…，N)，然后對連桿曲線進行精確擬合．規定esmax＜0.008和es＜0.005時滿足精確擬合精度要求．具體方法為:在連桿曲線上找到與擬合曲線的誤差最大點處插入一個型值點，更新原有的型值點并重新進行曲線擬合，如此反復進行t次，經過多次的試驗，取t=4已能滿足曲線擬合的誤差要求，不同形狀原始曲線的擬合情況見圖6，最大擬合誤差、平均擬合誤差如表1所示，可以看出擬合結果比較理想.

圖6 不同形狀的曲線擬合

表1 原始曲線的擬合誤差

為使神經網絡輸入特征參數的數目盡可能少，本文選擇將控制頂點順序連接成的控制多邊形各相鄰兩邊間的夾角θi(i=1，2，…，m+t)作為連桿曲線的特征參數．

至此，連桿軌跡曲線的特征參數提取完成．將大量的連桿曲線的特征參數θi(i=1，2，…，m+t)和對應機構的6個尺寸參數r1、r2、r3、r4、r5、δ 存儲，形成連桿曲線的電子圖譜庫．

5 尋找滿足給定軌跡要求的機構

本文選用廣義回歸神經網絡，利用已建立的電子圖譜庫中數據作為神經網絡訓練樣本，即m+t=16個控制多邊形各相鄰兩邊間夾角θi(i=1，2，…，m+t)作為輸入，對應6個機構尺寸參數r1、r2、r3、r4、r5、δ作為輸出，對神經網絡進行訓練并保存．

給定f個有序離散點(離散點數目f不受限制，可在4≤f≤N范圍內任意給定)，應用本文所述方法進行軌跡綜合，尋找滿足要求機構的步驟如下:

1)將給定的f個離散點進行B樣條曲線擬合，得到一條封閉的期望曲線．

2)利用與圖譜庫中連桿曲線相同的處理方法，對期望曲線進行歸一化處理，記錄此過程中期望曲線的6個歸一化參數:xG1、yG1、α1、xⅠ12、yⅠ13、k1，并對歸一化后期望曲線進行型值點的選擇以及特征參數的提取．

3)將期望曲線特征參數θ1，i(i=1，2，…，m+t)輸入到已訓練好并保存的神經網絡中，輸出與期望曲線對應的量綱一的機構尺寸參數(r2，1、r2，2、r2，3、r2，4、r2，5、δ2)，對應的機構為A2B2C2D2P2．

4)由于神經網絡具有自學習能力，輸出的滿足給定軌跡要求的機構尺寸參數可能并不對應圖譜庫中任何一組數據．因此，需要利用與圖譜庫中連桿曲線相同的處理方法，將輸出機構A2B2C2D2P2及其描繪的連桿曲線也進行一次歸一化處理，得到歸一化后機構A'2B'2C'2D'2P'2．

5)將歸一化后的期望曲線連同步驟4)中的機構A'2B'2C'2D'2P'2，按照步驟2)中記錄的6個歸一化參數進行反歸一化，得到滿足要求的實際機構A1B1C1D1P1及其實際參數(l1，1、l1，2、l1、3、l1，4、

l1，5、δ1)．

6)計算期望曲線與實際機構描繪的連桿曲線的綜合誤差，包括誤差平均值es和誤差最大值esmax．并計算誤差與期望曲線上最遠兩點間距離k1的比值，即Ks=es/k1和Ksmax=esmax/k1，將Ks、Ksmax作為度量在有量綱情況下軌跡綜合的精度參數．

反歸一化過程與歸一化過程相反，對歸一化后的機構和期望曲線進行反歸一化的具體方法如下:

a)將歸一化后的機構A'2B'2C'2D'2P'2和期望曲線放大k1倍，比例變換公式如式(8)所示，i代表反歸一化過程中需要進行坐標變換的各點的標號．

式中S1為比例變換矩陣．

b)判斷yⅠ13的正負性，若yⅠ13＜0，即期望曲線在歸一化時繞x軸進行了反射變換，則要對當前圖形做反射變換，反射變換公式如式(9)所示;若yⅠ13≥0，則不變化．

式中S'1為反射變換矩陣，且當yⅠ13＜0時，

當yⅠ13≥0時，

c)判斷xⅠ12和k1-xⅠ12的大小，若xⅠ12＞k1-xⅠ12，即期望曲線歸一化時先繞y軸進行了反射和平移變換，則將當前圖形繞y軸先做反射變換再平移，變換公式如式(10)所示;若xⅠ12≤k1-xⅠ12，則不變化．

式中:S'2為反射變換矩陣，T'1為平移變換矩陣．且當xⅠ12＞k1-xⅠ12時，

d)將當前圖形逆時針旋轉α1角，旋轉變換公式如式(11)所示:

式中R'1為旋轉變換矩陣．

e)將當前圖形平移，平移變換公式如式為

式中T'2為平移變換矩陣，得到實際機構A1B1C1D1P1．

反歸一化變換矩陣是以上6個變換矩陣的乘積，即

6 算法實現與示例

下面給出計算實例，給定16個離散點的坐標值(見表2)進行軌跡綜合，尋找近似通過這些離散點的曲柄搖桿機構.

表2 給定的離散點

應用本文所述的方法，首先，對給定的離散點通過B樣條曲線擬合得到期望曲線，如圖7(a).然后，對期望曲線經過歸一化處理，得到歸一化后的期望曲線如圖7(b)，以及6個歸一化參數(見表3).

圖7 綜合實例

表3 期望曲線的歸一化參數

然后，進行型值點選擇和特征參數提取，獲取的型值點和控制多邊形如圖7(c)和圖7(d)所示，得到期望曲線的特征參數 θ1，i(i=1，2，…，16)(見表4)．

表4 期望曲線的特征參數

將特征參數輸入到已保存的神經網絡中，輸出與期望曲線對應的機構尺寸參數r2，1=1．000，r2，2=3.037，r2，3=3.461，r2，3=2.500，r2，5=1.108，δ2=57.009°，對應的機構為A2B2C2D2P2．將機構A2B2C2D2P2及其描繪的連桿曲線進行一次歸一化，得到歸一化后的機構A'2B'2C'2D'2P'2，其各點的坐標為A'2(0.278，-0.275)，B'2(0.374，-0.641)，C'2(1.470，-0.290)，D'2(0.517，-1.191)，P'2(0.484，-0.236)，如圖7(e)所示.

最后，將機構A'2B'2C'2D'2P'2和歸一化后的期望曲線，按照期望曲線的6個歸一化參數xG1、yG1、α1、xⅠ12、yⅠ13和k1進行反歸一化，得到的軌跡綜合結果如圖7(f)所示．實際機構A1B1C1D1P1尺寸參數l1，1=22.729 mm，l1，2=69.036 mm，l1，3=78.671 mm，l1，4=56.824mm，l1，5=25.188 mm，δ1=57.009°，其各點的坐標為A1(22.723，-5.826)，B1(38.742，-21.950)，C1(84.949，29.342)，D1(62.771，-46.138)，P1(32.230，2.382)．綜合得到的機構連桿曲線與期望曲線的誤差和綜合精度參數分別為:誤差平均值es=0.657 mm，誤差最大值esmax=1.084 mm，Ks=1.10%，Ksmax=1.81%，能夠滿足軌跡綜合的精度要求．為進一步提高軌跡綜合的精度可以通過增加軌跡圖譜的數量、提高特征參數的數目等方式得到，在此不再詳述．

在主頻為2.54 GHz、奔騰處理器及內存為2 GB的計算機上利用本文所述方法綜合10條期望軌跡，只需要1.35 s就能給出與期望軌跡相對應的實際的曲柄搖桿機構，可見本方法具有非常快的綜合速度.

7 結 論

1)給出了基于三次非均勻B樣條曲線理論的連桿曲線特征提取方法，利用B樣條曲線控制多邊形各相鄰兩邊間的夾角作為連桿曲線的特征參數建立電子圖譜庫，減少了人工神經網絡輸入數據的數目.

2)通過連桿曲線歸一化方法，使重點集中在軌跡曲線的形狀上，忽略曲線的具體姿態，消除了由于坐標軸的選擇對軌跡綜合的影響，大大減少了電子圖譜庫中數據的冗余量.

3)通過程序自動獲取連桿曲線的型值點，避免了對大量形狀各異的連桿曲線的分類處理，大大簡化了軌跡綜合的過程.

4)本方法并不限制給定有序離散點的數目，將離散點擬合的期望曲線的特征參數輸入神經網絡進行特征匹配，試驗表明了該方法的有效性.

5)本文所提方法也適用于其他類型的平面四桿機構的軌跡綜合，如雙曲柄機構、雙搖桿機構和曲柄滑塊機構.

［1］CHANEKAR P V，GHOSAL A.Optimal synthesis of adjustable planar four-bar crank-rocker type mechanisms for approximate multi-path generation［J］.Mechanism and Machine Theory，2013，69:263-277.

［2］TARI H，SU H.A complex solution framework for the kinetostatic synthesis of a compliant four-bar mechanism［J］.Mechanism and Machine Theory，2011，46(8):1137-1152.

［3］MATEKAR S B，GOGATE G R.Optimum synthesis of path generating four-bar mechanisms using differential evolution and a modified error function［J］.Mechanism and Machine Theory，2012，52:158-179.

［4］CABRERA J A，ORTIZ A，NADAL F，et al.An evolutionary algorithm for path synthesis of mechanisms［J］.Mechanism and Machine Theory，2011，46(2):127-141.

［5］HONGYING Y，DEWEI T，ZHIXING W.Study on a new computer path synthesis method of a four-bar linkage［J］.Mechanism and machine theory，2007，42(4):383-392.

［6］VASILIU A，YANNOU B.Dimensional synthesis of planar mechanisms using neural networks:application to path generator linkages［J］.Mechanism and Machine Theory，2001，36(2):299-310.

［7］ULLAH I，KOTA S.Optimal synthesis of mechanisms for path generation using Fourier descriptors and global search methods［J］.Journal of Mechanical Design，1997，119(4):504-510.

［8］王成志，紀躍波.小波分析在平面四桿機構軌跡綜合中的應用研究［J］.機械工程學報，2004，40(8):34-39.

［9］GALáN-MARíN G，ALONSO F J，DEL-CASTILLO J M.Shape optimization for path synthesis of crank-rocker mechanisms using a wavelet-based neural network［J］.Mechanism and Machine Theory，2009，44(6):1132-1143.

［10］張新歌.基于神經網絡的鉸鏈四桿機構復演軌跡設計軟件的開發［D］.蘇州:蘇州大學，2008.

［11］褚金奎，孫建偉.基于傅里葉級數理論的連桿機構軌跡綜合方法［J］.機械工程學報，2010，46(13):31-41.

［12］郎內斯J A，納耳桑G L.四連桿機構分析圖譜［M］.李學英，譯.北京:機械工業出版社，1966.

［13］PIEGL L A，TILLER W.The NURBS book［M］.New York:Springer，1997.

［14］PIEGL L A，TILLER W.Surface approximation to scanned data［J］.The visual computer，2000，16(7):386-395.

［15］PIEGL L A，TILLER W.Biarc approximation of NURBS curves［J］.Computer-Aided Design，2002，34(11):807-814.