多分支水平井參數智能優化技術

趙廣淵　蘇玉亮　任　龍　郝永卯　李　政　王文東（1.中海油田服務股份有限公司，天津　0045；.中國石油大學（華東）石油工程學院，山東青島　66580；.中海石油（中國）有限公司天津分公司，天津　00456）

多分支水平井參數智能優化技術

趙廣淵1，2蘇玉亮2任龍2郝永卯2李政3王文東2
（1.中海油田服務股份有限公司，天津300452；2.中國石油大學（華東）石油工程學院，山東青島266580；3.中海石油（中國）有限公司天津分公司，天津300456）

多分支水平井參數優化設計是一個多目標最優化問題，采用傳統的優化方法求解復雜程度依賴于優化對象數目，且容易產生局部收斂。基于多分支水平井的油藏數值模擬技術，以生產凈現值為目標函數，應用遺傳算法建立了多分支水平井參數智能優化設計方法，并編程實現了優化設計的全程自動化。優化過程中，利用正交設計原理生成種群初值，避免了初始種群的隨機盲目性；根據個體適應值大小選擇交叉和變異概率，保證了種群的多樣性和算法的全局收斂能力。以珠江口盆地某海上低滲透油藏為例進行了多分支水平井參數優化設計，結果表明：遺傳算法優化具有全局智能搜索尋優的特點，優化結果比傳統優化算法有較大提高，具有較強的優越性和實用性。

多分支水平井；智能優化；遺傳算法；正交設計；適應值；交叉概率；變異概率

多分支水平井目前已廣泛應用于各類油藏的開發實踐中，因其具有井眼與油藏接觸面積最大（MRC）的特點，可以提高單井產能，減少生產井數，降低開發成本，尤其在海上可以減少平臺和水下底盤的開槽數，減少地表設施及甲板空間需求［1-3］。在采用多分支水平井開發時，參數合理配置是實現開發效果的關鍵，因此為了盡可能獲得最大的生產效益，必須對多分支水平井參數進行優化設計。多分支水平井參數主要包括：主井筒長度、分支長度、分支角度和分支數目等，對其優化設計是復雜的多目標規劃問題。目前常采用的方法主要有單因素分析和正交實驗設計的方法［4-5］，但都存在可行解空間難以全部覆蓋、優化對象數目增加導致模擬方案數量大幅度增加等問題。為此，筆者提出利用遺傳算法對多分支水平井參數進行智能優化，并且編程將整個優化過程自動化，通過實例計算驗證了該算法的優越性。

1　智能優化系統建立

遺傳算法是一種啟發式算法。它的基本思想是模擬自然界的生物遺傳和進化現象，將問題的可行解進行二進制編碼，表述為染色體，通過對染色體進行交叉、變異、選擇等操作，使染色體構成的整個種群性狀趨向最優。通過遺傳算法的基本操作，可以在所有可行解空間中進行有導向性的、基于自然選擇和遺傳原理的智能搜索，逐步逼近最優解，從而避免了對整個解空間進行窮舉式的搜索。它不要求搜索空間是連續的、可微的和單峰值的，適用于相當復雜的非線性解空間尋優問題［6-10］。因此，可以通過建立基于遺傳算法的智能優化系統來解決多分支水平井的參數優化問題。

1.1優化目標函數

多分支水平井的參數優化是復雜的多目標、非線性解空間尋優問題。經調研和開發實踐發現，多分支水平井的主要優化參數有主井筒長度、分支長度、分支角度和分支數目4個參數，這些參數對開發效果影響顯著，且相互之間交叉影響。為研究各參數的最佳組合關系，作出如下假設：（1）均質盒狀油藏中央有一口多分支水平井開發；（2）各分支長度相同，且在主井筒上的分支節點間距相等。

多分支水平井參數優化設計，即調整各個參數使優化目標函數值達到最優。利用遺傳算法進行優化時，對種群中個體的適應度評價需要直接利用優化目標函數，目標函數值又叫適應值。選取生產凈現值為優化的目標函數f，其表達式為

式中，Qo、Qw分別是貼現期n的產油量、產水量，m3；Co、Cw分別是相應流體的盈利或損失，元/m3；i是年利率，%；Y是貼現期總數；Cwell是鉆完井的總成本（因油田地理位置和條件而不同），元。

鉆完井的總成本Cwell定義如式（2）

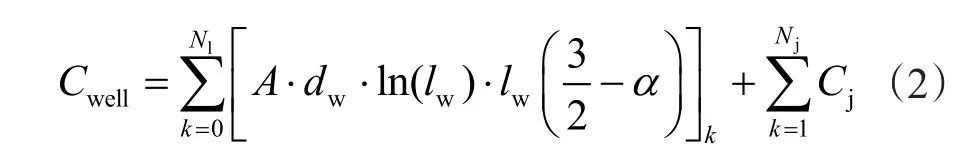
式中，Nj是主井筒上的分支節點數，個；Nl是從節點上延伸出來的分支數，個；dw為井筒直徑，m；lw為主井筒或者單分支的長度，m；Cj是分支節點磨銑的費用，元/個；A是轉換系數，與油田位置和鉆井條件有關；α代表井的斜度，鉆直井和水平井的成本可以用參數（1.5-α）轉換。特殊地，直井α=1，水平井α=0，說明水平井單位長度的鉆井成本是直井的3倍。

式（1）中的產量矢量從數值模擬器中獲得，然后代入其他參數，即可求得適應值。

1.2多分支水平井模型建立

采用Eclipse軟件中的多段井模型（Multisegment Well Model）對多分支水平井進行模擬，井筒中的變質量流通過離散的段結構來精確描述（圖1），網格塊與其相連的分段節點之間的流體流入動態關系式［11］為

式中，qpj為網格塊j處p相的體積流速（當流體從地層流向井筒時取正，從井筒流入地層取負），m3/d；Twj為網格塊j處的連接傳導率，m·（mPa·s）/（MPa·d）；Mpj為網格塊j處p相的流度，m2/（mPa·s）；j為網格塊j處壓力，MPa；Hcj為分支節點c和網格塊j之間的靜水柱壓力，MPa；n為分段節點n處的壓力，MPa；Hnc為分段節點n和連接點c之間的靜水柱壓力，MPa。

圖1　段結構示意圖

1.3初始種群的生成方法

通常遺傳算法的初始種群是隨機生成的，具有一定的盲目性，各個個體很難保證均勻分布于整個解空間中，使得個體在初始階段就有可能失去了對某些區域的搜索能力，盡管在遺傳后代中可能會對這一區域進行搜索，但降低了搜索效率［12］。而正交試驗設計是研究多因素多水平的一種設計方法，是根據正交性從全部試驗中挑選出部分具有代表性的點進行試驗，具有“以點代面”的特點，這些有代表性的點具備了“均勻分散、整齊可比”的特點。因此考慮將正交試驗設計的原理引入初始種群的生產方法中，避免隨機生成初始種群中的個體盲目性。

采用如下方法對種群初始化：（1）根據多分支水平井的4個參數（即4個因素）的取值區間，將區間拆分成b-1個子區間（對應b個水平）；（2）構建a行正交設計表，設計出試驗方案；（3）根據各方案參數，利用多段井模型建立多分支水平井數值模擬模型，計算多分支水平井產量矢量，并代入目標函數，求得適應值；（4）按照適應值從大到小排序，取前n個個體作為初始種群。

由此生成的初始種群，可覆蓋整個解空間，有效地避免了隨機生成初始種群初期搜索的盲目性，提高了尋優效率。

1.4交叉概率和變異概率的選取方法

交叉和變異操作是遺傳算法中的最主要操作。通過交叉操作可得到新一代個體，新個體組合了父輩個體的特性。變異是在種群中選擇一個個體，對于選中的個體以一定的概率隨機的改變基因中的編碼值。因此，交叉概率和變異概率的選取是影響遺傳算法行為和特性的2個關鍵因素。交叉概率越大，新個體產生速度越快，增加了種群的多樣性，但存在較優個體結構被破壞的風險；而交叉概率過小，又會使種群多樣性下降，進化速度太慢。同時如果變異概率過小，則不利于新個體的產生；變異概率過大，則遺傳算法的搜索盲目性會過大。因此采用自適應性遺傳算法的交叉概率和變異概率的選取［13］，計算方法為

1.5遺傳算法優化總體設計

基于遺傳算法的多分支水平井參數優化步驟（圖2）主要有：

（1）確定多分支水平井的主井筒長度、分支長度、分支角度和分支數目4個參數的取值范圍，按照前述方法生成初始種群；

（2）將初始種群中的n個個體分別轉化為N個二進制編碼，根據式（4）和式（5）計算每個個體的交叉概率和變異概率，并進行遺傳運算，得到下一代的新個體；

（3）將得到的個體逐個解碼，建立多分支水平井數值模擬模型，計算產量矢量，并利用目標函數評價每一個個體的適應度；

（4）判斷是否達到收斂條件，如果達到收斂條件，停止運算，輸出優化結果；如果未達到收斂條件，根據每一個個體的適應值大小，利用輪盤賭模型進行選擇操作，然后返回步驟（2）繼續優化，直到滿足收斂條件。

圖2　多分支水平井參數智能優化流程圖

應用MATLAB軟件編制了遺傳算法優化多分支水平井參數的程序，實現了從參數二進制編碼、解碼，調用數值模擬軟件建立多分支水平井模型，計算結果的讀取，以及遺傳操作，優化目標函數的計算等整個流程的智能化操作，形成了多分支水平井參數智能優化設計系統，降低了計算工作量，使算法具備了較強的實用性。

2　應用實例

珠江口盆地某海上A油藏為強底水、低滲透油藏，經過強底水驅掃后，定向井、水平井總體呈現低產能、特高含水的特點，為此計劃采用多分支水平井開發，從而達到提高單井產能、緩解底水上升的目的。

根據文中提出的優化思路，以A油藏的實際資料為基礎建立油藏數值模型，利用遺傳算法對多分支水平井參數優化設計。該油藏原始油水界面-2 506 m，平均孔隙度15%，平均滲透率20 mD，油層厚度12 m，原始地層壓力24.8 MPa，地層原油黏度3.88 mPa·s，原油體積系數1.24。采用定井底流壓10 MPa開發10 a，以10年末的生產凈現值為優化目標函數。計算過程中，僅考慮非對稱性多分支水平井，即Nl=1。取產油的盈利為3 860元/m3，產水的成本為30元/m3，A=980元/m3，Cj=20 000元/個。

首先確定多分支水平井的參數取值范圍如表1。將4個參數的取值范圍分別劃分為4個子區間，即對應5個水平，因此可以構建L25（56）的正交表，將各個參數組合分別利用多段井模型建立多分支水平井的數值模擬模型，計算井的產量矢量，并代入式（1）評價適應值大小，然后排序選擇出20個方案作為初始種群。對初始種群中的20個體進行二進制編碼，然后根據式（4）和式（5）計算交叉概率和變異概率，進行選擇、交叉、變異等操作。計算至連續5代的個體平均適應值接近終止優化。

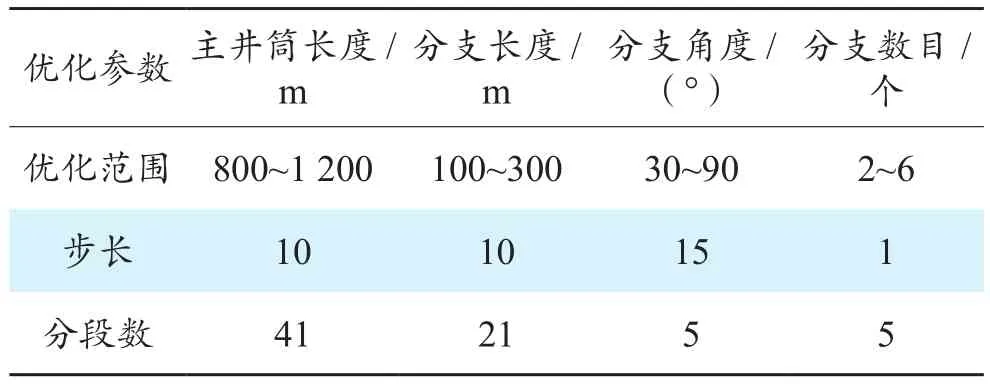
表1多分支水平井優化參數取值范圍

由計算結果（圖3）可知，隨著遺傳代數的逐漸增加，種群個體的平均適應值總體呈現逐漸上升的趨勢，由最初的350.8萬元增加到最終的360.6萬元，種群的總體質量得到大幅度提升。而個體的最優適應值經過3代的計算后即趨于穩定，得到的最優主井筒長度為1 080 m，分支長度為300 m，分支角度為75°，分支數目為3個。與正交試驗設計方法得到的尋優結果對比可知，遺傳算法的優化結果有較大的提高，而且其搜索步長小，極大地拓展了最優解的搜索空間。

圖3　多分支水平井智能優化結果

根據設計結果，結合A油藏構造及儲集層特征，在構造頂部“甜點”位置設計了多分支水平井16 MH井，為三分支水平井，其中主井筒長度1 053 m，分支1、2、3的長度分別為289 m、315 m、295 m，分支角度為60～80°。16MH井投產后，初期產能高達396 m3/d，含水率3.67%，截至2013年10月已生產20個月，累計產油4.35×104m3，實現了海上低滲透油藏的有效開發。

3　結論

（1）遺傳算法具有導向性智能搜索的特點，對復雜的多目標、非線性解空間尋優問題有很好的適應性。利用遺傳算法進行多分支水平井參數優化，在可行解全空間搜索最優解，方法可行而有效。

（2）遺傳算法中利用正交設計原理生成初始種群，以及根據個體適應值自動選取交叉概率和變異概率的2種措施，有效地提高了遺傳算法的尋優效率。通過編制程序，高效地實現了多分支水平井參數的智能優選操作，大幅度地降低了人工操作工作量。

（3）實例分析結果表明，遺傳算法比正交設計方法的優化結果有較大提高，搜索空間廣，具有較強的優越性，對現場實施有很一定的指導意義。

［1］曾傳云，譚勇志，徐紅國，等.多分支水平井鉆井技術在玉平8井的應用［J］.石油鉆采工藝，2013，35（4）:22-25.

［2］劉亞軍，張曉誠，張海，等.旅大A3h水平分支井鉆井技術［J］.石油鉆采工藝，2010，32（6）:35-37.

［3］AHMED Y B, SAUDI A， MOHAMMAD M F, et al. Optimization of multilateral well design and location in a real field using a continuous genetic algorithm［R］. SPE 136944, 2010.

［4］張世明，周英杰，宋勇.魚骨狀分支水平井井形設計優化［J］.石油勘探與開發，2011，38（5）:606-612.

［5］王曉冬，于國棟，李治平.復雜分支水平井產能研究［J］.石油勘探與開發，2006，33（6）:729-733.

［6］黃輝，吳曉東，孫天禮.基于遺傳算法的低滲透氣藏水平井壓裂參數優化［J］.天然氣工業，2008，28（5）:91-93.

［7］李俊鍵，馬佳，劉勇，等.基于代理模型與遺傳算法的海上油田聚合物驅注入參數優化控制方法［J］.中國海上油氣，2012，24（4）:41-44.

［8］柳毓松，廉培慶，同登科，等.利用遺傳算法進行水平井水平段長度優化設計［J］.石油學報，2008，29（2）:296-299.

［9］BURAK Y, LOUIS J D, KHALID A. Optimization of nonconventional well type, location and trajectory［R］. SPE 77565, 2002.

［10］周偉，孫樹棟.遺傳算法原理及其應用［M］.北京:國防工業出版社，1999:20-48.

［11］孫明，楊銀山，朱紅宇，等.魚骨井井型參數對開發動態指標影響研究［J］.特種油氣藏，2012，19（2）:62-65.

［12］張鳳喜，陳明，馬國新，等.一種優化壓裂水平井井網參數的新方法［J］.斷塊油氣田，2010，17（6）:751-754.

［13］樊冬艷，姚軍，姚婷，等.基于自適應遺傳算法的壓裂水平井參數優化［J］.油氣地質與采收率，2011，18（5）:85-88.

（修改稿收到日期2014-10-15）

〔編輯薛改珍〕

Intelligent optimization technology for parameters of multi-branch horizontal well

ZHAO Guangyuan1,2, SU Yuliang2, REN Long2, HAO Yongmao2, LI Zheng3, WANG Wendong2
（1. China Oilfield Services Limited, Tianjin 300452, China; 2. Petroleum Engineering College, China University of Petroleum (Huadong), Qingdao 266580, China; 3. Tianjin Branch of CNOOC China, Tianjin 300456, China）

Parameter optimization design for multi-branch horizontal well is an issue of multi-objective optimization. The complexity of optimization method solution using traditional method depends on the number of optimized objects, and local convergence may occur easily. Based on reservoir numerical simulation technique for multi-branch horizontal well and taking the net present value of production as the objective function, the intelligent optimization design method for parameters of multi-branch horizontal well was established using genetic algorithm and the whole-course automaton of optimization design was achieved by programming. During optimizing, the orthogonal design principle was used to generate the initial value of the population, which avoided the random blindness of initial population. The probability of crossover and mutation was selected according to individual fitness value, which ensured the diversity of the population and global convergence ability of the algorithm. An offshore low-permeability oil reservoir at Zhujiang River Mouth Basin was used as an example to carry out optimization design for parameters of multi-branch horizontal well, and the result showed that the genetic algorithm optimization had a feature of global intelligent search optimization, and the optimization results were improved greatly compared with traditional optimization algorithm. So this method has significant superiority and practicability.

multi-branch horizontal well; intelligent optimization; genetic algorithm; orthogonal design; fitness value; crossover probability; mutation probability

TE355.6

A

1000 – 7393（ 2015 ） 02 – 0008 – 04

10.13639/j.odpt.2015.02.003

國家科技重大專項“大型油氣田及煤層氣開發”（編號：2011ZX05051）。

趙廣淵，1988年生。主要從事海上低滲透油氣田開發及數值模擬方面的研究。電話：15066193862。E-mail：zhaogy0806@163. com。

引用格式：趙廣淵，蘇玉亮，任龍，等.多分支水平井參數智能優化技術［J］.石油鉆采工藝，2015，37（2）：8-11.