基于HHT法的煤沖擊破壞低頻電磁信號去噪

付玉凱，楊 威，李成武

(1.天地科技股份有限公司開采設計事業部，北京100013;2.煤炭科學研究總院開采設計研究分院，北京100013;3.煤炭科學研究總院煤炭資源高效開采與潔凈利用國家重點實驗室，北京100013;4.中國礦業大學 (北京)資源與安全工程學院，北京100083)

隨著煤礦開采深度的增加，煤礦煤巖體動力災害日益增多，嚴重影響了煤礦的安全、高效生產。針對煤巖體動力災害，預測預報是關鍵。目前，電磁輻射預測方法受到了國內外學者的關注［1－3］。

由于煤巖沖擊破壞過程中產生的電磁信號是一種非線性、陣發性的脈沖信號，屬于典型的非平穩隨機信號［4］，所以對其進行去噪濾波顯得非常困難。因此，去噪濾波技術嚴重制約了電磁信號在預測預報煤巖動力災害中的應用。目前，學者主要采用傅里葉變換 (FFT)、小波變換 (WT)等信號處理方法對電磁信號進行分析，但是這些方法只能分析信號的總體頻率，不能有效分析信號的時頻特性［5－6］。小波變換分析方法與其他分析方法相比，其時頻分析精度依賴于小波基函數的選取，有時由于基函數選取問題，使其對信號的精細分解受到限制［7－8］。

希爾伯特黃變換 (HHT)是1998年由Huang等人［9－10］提出了一種處理非線性、非平穩信號的時頻分析方法，HHT分析方法主要包括2個部分:一是多分辨經驗模態分解 (EMD)和瞬時頻率變換;二是對EMD分解的分量進行時頻分析。HHT變換實際上是一種以傅里葉變換為基礎的改進型信號處理方法，該方法在電磁信號去噪中的應用較少。

本文采用HHT時頻分析方法對煤沖擊破壞的低頻電磁信號進行經驗模式分解 (EMD)，并通過對各個IMF(某一頻率尺度上的模態信號)分量進行重構，最后對重構信號進行時頻譜分析。

1 HHT變換原理

1.1 經驗模態分解法 (EMD)原理及算法

1.1.1 EMD原理

EMD法［11］是 HHT的核心，其主要有兩個作用:過濾疊加波和對稱化波形。EMD可以將信號從時間尺度上進行IMF分量分解，但是需要滿足下面兩個條件:

(1)整個信號數據的極值點和過零點個數相差不超過1。

(2)由局部最大值所繪制的包絡線和由局部最小值點所繪制的包絡線的平均值為0，就是信號必須對稱于時間軸。

1.1.2 EMD算法

對一個原始信號X(t)，首先找出X()t上全部的最大值和最小值，然后采用插值方法對曲線進行極值擬合，從而繪制出曲線的包絡線Xmax()t。同理得出包絡線Xmin()t，2條包絡線包含了全部信號數據。對2條包絡線取其平均值得平均線m1()t，再用X()t減掉m1()t得到h1()t。如果信號不同，h1()t有可能產生一個IMF分量，也可能得到2個IMF分量。若分量不滿足限定條件，此時將h1()t當做原信號，重復以上的程序，即得h11()t =h1()t －m11()t，m11()t是h1()t的2條包絡線平均值;若h11()t沒有變換成IMF分量，則接著計算，進行k次計算，得到第k次計算的數據h1k(t)=h1(k－1)(t)－m1k(t)。判斷h1k(t)是不是可以滿足IMF分量，這樣就需要一個計算過程終止的法則，一般可以用2個連續結果的標準差SD作為判斷依據［12－13］:

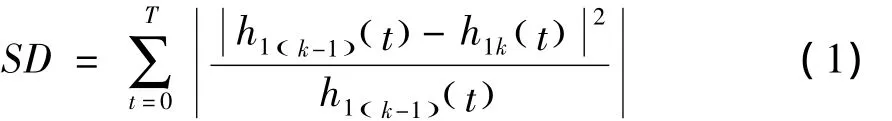
在實際運算中，可以通過對信號反復篩選來確定IMF分量，篩選結果通過SD值來確定。經驗表明，當取SD=0.2～0.3時比較合適，既可確保IMF的線性和穩定性，又可使IMF具有相應的物理意義［11］。

1.2 HHT變換與時頻譜

1.2.1 HHT 變換

對信號進行分解，得到IMF分量，對分量進行HHT變換，計算出其瞬時頻率。對全部IMF分量進行上述變換，即HHT譜［10］。HHT變換很好地刻畫了信號的局部性質，可以很好地得到信號的瞬時頻率，避免了傅里葉變換中產生的不真實高低頻成分，其具有直觀的物理意義［10］。

1.2.2 HHT譜

HHT譜變換［14］可以把信號幅值變換為時間、頻率平面上的等高線圖，該變換稱之為HHT時頻譜。時頻譜主要有3種表達形式:灰度圖、等高線及三維空間圖形，其表達式如下:

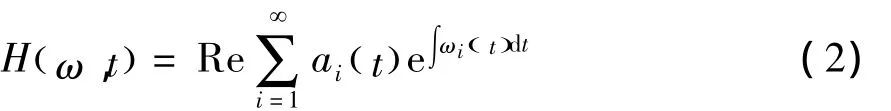
式中，H為信號幅值;Re為累計相加;ai()t為每一階IMF的幅值;ωi(t)為每一階IMF的瞬時頻率。

如果對Hω，()t進行時間上積分，可以得到信號的HHT邊際譜:

2 實驗簡介

2.1 實驗系統及裝置

試驗系統包括兩部分，即霍普金森壓桿(SHPB)和電磁輻射測試系統，試驗系統見圖1，圖2。

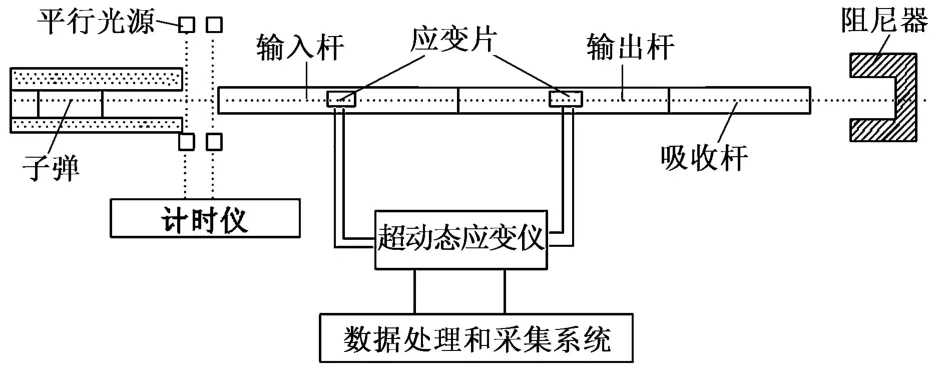
圖1 實驗裝置

圖2 實驗裝置實物

霍普金森壓桿系統由子彈、輸入桿和輸出桿組成，壓桿為鋼質壓桿，直徑為50mm，子彈為φ50mm×400mm的圓柱體。被測試樣夾在輸入桿和輸出桿之間。

選用的電磁輻射接收裝置為ZDKT－1型瞬變磁振測試系統 (圖2)，該系統包括磁場天線、信號采集系統 (3000s－1)及計算機。實驗時，天線正對煤試件，距其30～40mm。

2.2 煤樣制作

煤試件來源于某礦掘進頭，煤樣采用圓柱體，尺寸為 φ50mm ×50mm，平行度0.02mm［15］，試樣兩端涂抹石墨，以減少其摩擦效應［16－17］。

2.3 煤沖擊破壞低頻電磁信號去噪前分析

共加工12個試樣，分為4組進行實驗，分別記為 A1，A2，A3;B1，B2，B3;C1，C2，C3;D1，D2，D3。對每一組進行相同速率下的實驗，由于煤體強度較低，經多次沖擊測試發現，沖擊速率大于3m/s即可破壞煤試樣，且沖擊速率過大會導致應力－應變曲線失真。當沖擊速率在3～10m/s之間時，測試結果可靠性較高。由于子彈沖擊速率是由動力系統中的高壓氮氣所施加的，其速率控制有一定的誤差，所以沖擊加載速率以平行光源測試結果為準。根據平行光源測定結果，實驗的沖擊速 率 分 別 為 3.287m/s，6.251m/s，6.950m/s，8.714m/s。實驗結果發現，同一組實驗結果的重復性較好。鑒于文章篇幅有限，以D1為典型信號進行分析，沖擊速率為8.714 m/s時，最大應變率為166.35s－1，采集的低頻磁場原始信號見圖3。

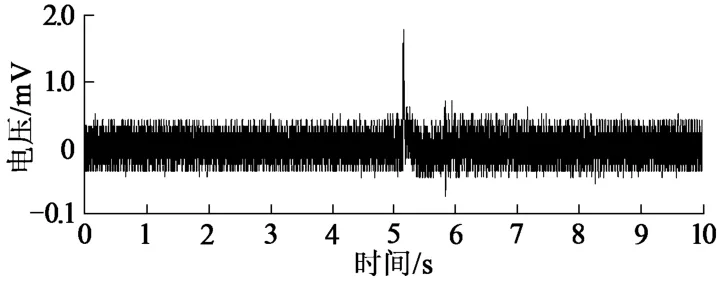
圖3 原始信號

由圖3可以看出，共采集了10s的低頻磁場信號，但突變的低頻磁場信號介于5～7s之間，持續時間較短 (小于2s)，并且信號中伴隨著大量的背景噪聲信號，這些噪聲信號主要來自外界環境和采集系統自身［18］。存在噪聲的低頻電磁信號對于預測煤巖沖擊破壞十分不利。為了能清楚地認識低頻磁場信號的特征，需要對原始低頻電磁信號進行去噪分析。為了驗證HHT分析煤沖擊破壞的低頻磁場信號的有效性和突顯信號非線性的能力，首先將原始低頻磁場信號進行FFT頻譜分析和Morlet時頻分析［19－20］。Morlet時頻分析是小波變換的一種形式，分析結果見圖4和圖5。

由圖4和圖5可以看出，信號的能量主要集中在600Hz以內，原始低頻信號中存在明顯的噪聲成分，并且Morlet的時頻分析譜的有效信號也被背景噪聲信號掩蓋，從上面2個圖很難清楚認識有效信號隨時域和頻域的動態變化特征，這就需要進一步采用HHT法對信號進行去噪分析。

圖4 原始信號的FFT譜

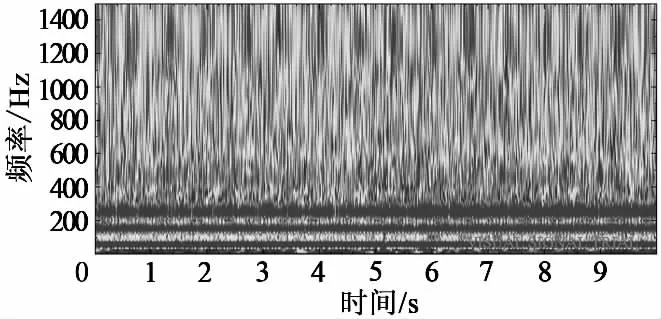
圖5 原始信號的Morlet時頻譜

3 低頻磁場信號的HHT分析

3.1 磁場信號的EMD分解及重構

低頻電磁信號屬于非平穩脈沖信號，在煤巖沖擊破壞過程中有時某一時間段的信號強度大，那么信噪比就較高;而另一時間段信號強度較弱，這時信噪比就很低。如果采集到的信號強度一直較低，那么會嚴重影響信號的采集質量［21］。如果在信號分析時，我們能選擇能量強的信號進行分析，而舍棄那些能量弱的信號 (信號強弱跟煤巖體破裂程度相關)，這樣才能得到原始信號中的有效信號。其他信號處理方法難以完成上述問題，這也是HHT方法能完成這一問題的關鍵。

首先運用HHT中的經驗模態分解方法，即EMD分解，可以得到原始低頻磁場信號的有限數目的IMF分量。由于信號的特征尺度參數都是基于所采集信號，所以，EMD所篩分出來的IMF分量都具有實際物理意義，每個IMF分量代表了某一頻率尺度上的模態。圖6是低頻電磁信號的EMD分解圖，該信號共分為11階IMF分量，在時間域上表示從小尺度到大尺度的層層篩選濾波。

從圖6可以看出，IMF_h1～IMF_h5分量包含大量的噪聲信號 (外界環境噪聲和采集系統噪聲);IMF_h6～IMF_h10分量噪聲信號較低，其屬于低頻磁場信號的優勢分量，為信號優勢頻率分量;IMF_residual分量表示磁場信號的變化趨勢，通常稱之為殘余分量。

將IMF_h6～IMF_h10分量進行重構，重構信號見圖7所示。由圖7可以看出，重構的信號能很清晰地刻畫出低頻磁場信號的非線性、非平穩性，很好地表示出了信號的時頻特征——磁場信號初期線性上升，然后指數衰減，最后尾部小幅震蕩［22－23］。

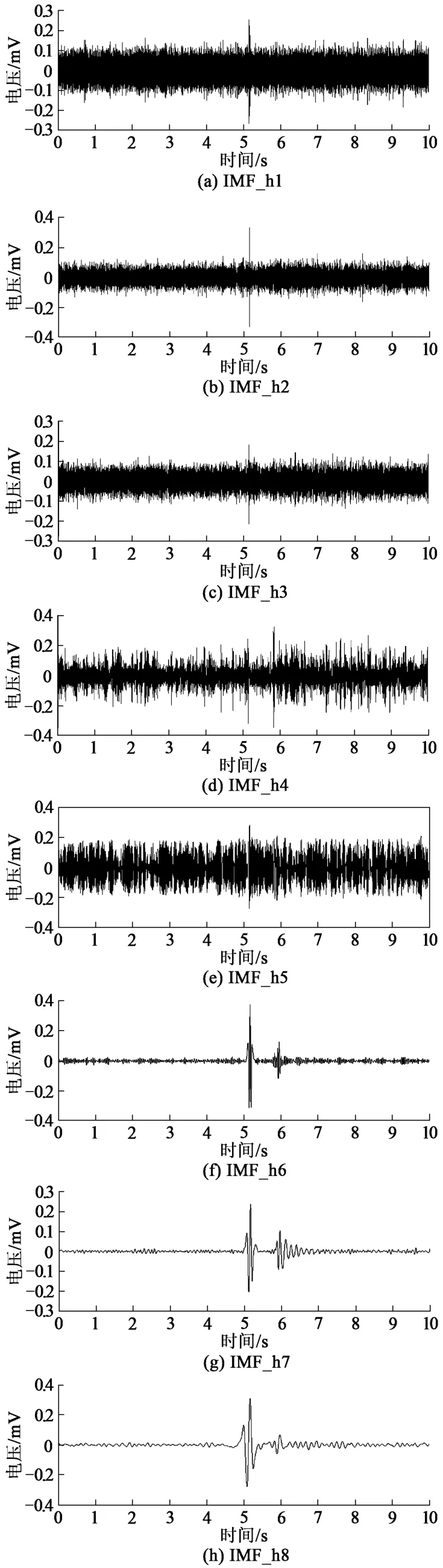
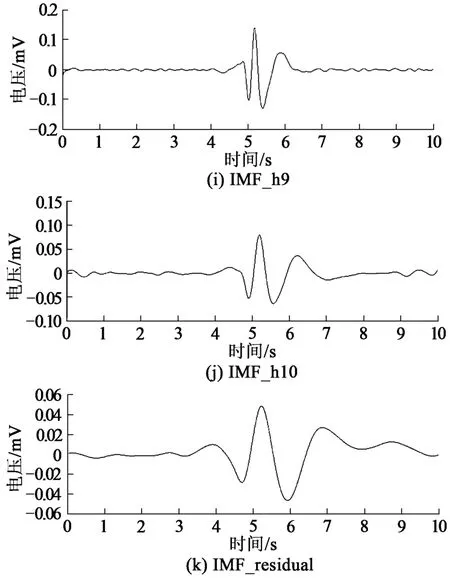
圖6 原始信號EMD分解

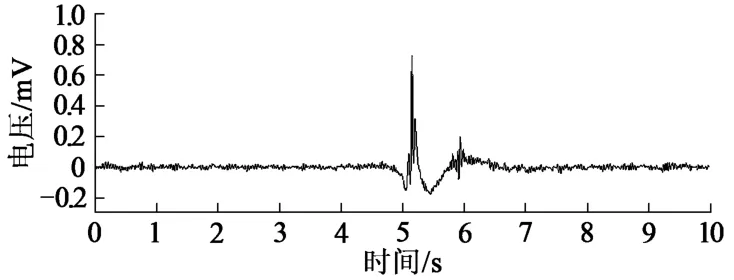
圖7 去噪重構信號

將重構的信號進行FFT變換，得到信號的幅值－頻率圖 (圖8)。由圖8可以看出，煤沖擊破壞產生的低頻磁場信號的優勢頻率較低，范圍在0～40Hz之間，對另外幾組煤樣進行實驗。采用上述分析方法后，分析結果基本相同。

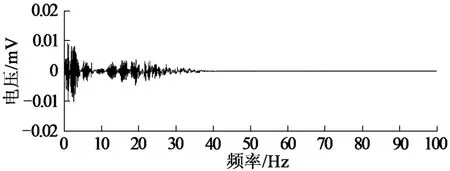
圖8 重構信號的頻域

3.2 重構信號的時頻譜分析

圖9 (a)是對重構信號進行的HHT時頻譜，從圖中可以看出，顏色越亮表示其能量越高，反之越低;HHT時頻譜直觀地表現出了信號的聚集性，與原始信號的時頻譜 (圖5)相比，可以很清晰地看出能量隨時間和頻率的變化。顯然，在0～100Hz頻段內，整個時域上的能量都較強;在時間域上，第5s至第6s時間域上的能量較強，該時間域對應于煤的沖擊破壞時間。

圖9(b)表示重構信號的邊際時間，表示每個時間在全局上的幅度之和，是表示時間點上信號能量強弱的一個指標，從該圖中也可以看出，第5s至第6s時間域上的能量較強，很好地驗證了HHT時頻譜分析的正確性。

圖9(c)表示重構信號的邊際譜，表示在每個頻域上全部幅值的總和，由圖可以看出，0～40Hz范圍的邊際譜比較大，這也說明了信號能量的主要頻域集中在0～40Hz，分析結果與圖8相吻合。

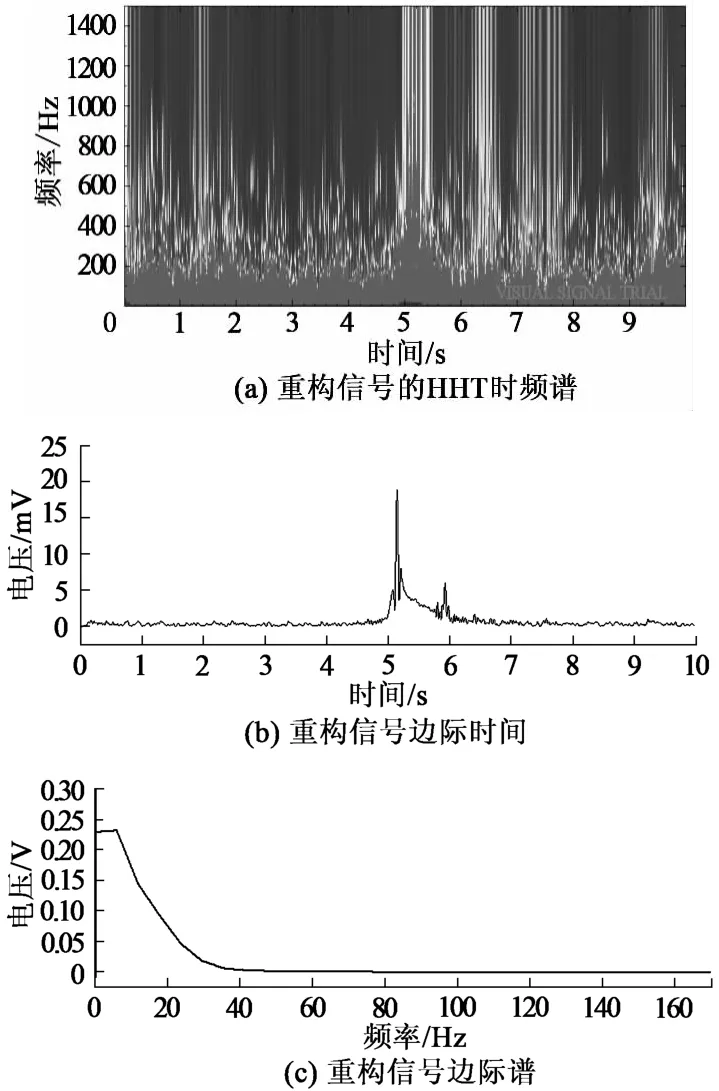
圖9 重構信號的HHT時頻譜、邊際時間和邊際譜

總之，HHT方法可以有效地對煤沖擊破壞的低頻磁場信號進行濾波去噪，可以很好地表示磁場信號的時頻動態非線性、非平穩性及脈沖特性，可以表現出信號時域上的頻率和能量差異，與其他信號處理方法相比，有其獨特的優勢。由上述分析可以看出，HHT時頻分析方法為煤巖體沖擊破壞磁場信號的濾波處理提供了一種新的方法。

4 結論

(1)采集到的煤沖擊破壞低頻電磁信號持續時間較短 (1～2s)，并且信號中存在大量的背景噪聲。通過對原始信號進行FFT頻譜分析和Morlet時頻分析，得出原始信號的能量主要集中在600Hz以內;并且Morlet時頻分析譜的有效信號被背景噪聲信號完全掩蓋。

(2)HHT法中的EMD可以很好地分解原始磁場信號，然后得出其IMF分量，每個IMF分量都有其特定的物理意義，通過對有效IMF分量進行重構，重構信號能很好地刻畫出低頻電磁信號的非線性、非平穩性及脈沖特性。

(3)通過對重構信號進行時頻譜分析，可以很清晰地看出能量隨時間和頻率的變化，并且得出低頻磁場信號的優勢頻率在0～40Hz之間，能量最強點位于信號的第5～6s之間。

(4)與其他分析方法相比，HHT分析方法具有完全的局部時頻特征，可以準確地刻畫低頻磁場信號的動態變化特征，且可以很好地刻畫信號的突變點信息，這為低頻電磁信號的檢測、信號濾波、數據篩選等提供了有利條件。

［1］何學秋，劉明舉.含瓦斯煤巖破壞電磁動力學［M］.徐州:中國礦業大學出版社，1995.

［2］王恩元，何學秋.煤巖變形破裂電磁輻射的實驗研究 ［J］.地球物理學報，2000，43(1):131－137.

［3］聶百勝，何學秋，王恩元，等.煤體剪切破壞過程電磁輻射與聲發射研究 ［J］.中國礦業大學學報，2002，31(2):609－611.

［4］朱郴韋.煤體破裂電磁輻射信號波形特征及降噪方法研究［D］.北京:中國礦業大學 (北京)，2009.

［5］Cohen L.Time－frequency analysis［M］.New Jersey:Prentice Hall，1995.

［6］謝 中，程迎軍，徐清燕.電解氣泡析出時電位波動的頻譜分析［J］.中國有色金屬學報，2003，13(4):1011－1016.

［7］劉希靈，李夕兵，洪 亮，等.基于離散小波變換的巖石SHPB測試信號去噪［J］.爆炸與沖擊，2009，29(1):67－72.

［8］周子龍，李夕兵，龍八軍.巖石SHPB試驗信號的小波包去噪［J］.巖石力學與工程學報，2005，24(S1):4780－4783.

［9］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non－station time series analysis［C］.Proceeding of the Royal Society of London，1998.

［10］Yue H Y，Guo H D.A SAR.Interferogram filter based on the empirical mode decomposition method［C］.Proceedings of Geosoience and Remote Sensing Symposium.IGARSS O1，2001.

［11］Semion Kizhner，Thomas P Flatley，et al.On the Hilbert－ Huang transform data processing system development［A］.2004 IEEE Aero pace Conference Procedings［C］.2004:1961－1979.

［12］李夕兵，凌同華，張義平.爆破震動信號分析理論與技術［M］.北京:科學出版社，2009.

［13］Norden E Huang，Zheng Shen，Steven R Long，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non－stationary time series analysis［J］.The Royal Society，1998，454:903－995.

［14］武安緒，吳培稚，蘭從欣，等.Hilbert－Huang變換與地震信號的時頻分析［J］.中國地震，2005，21(2):207－216.

［15］李勝林，劉殿書，李祥龍，等.75mm分離式霍普金森壓桿試件長度效應的實驗研究［J］.中國礦業大學學報，2010，39(1):93－97.

［16］ZENCKER U，CLOS R.Limiting conditions for compression testing of flat specimens in the Hopkinson pressure bar［J］.Experimental Mechaincs，1998，39(4):343－348.

［17］WEINONG W，CHEN B S.Split Hopkinson(Kolsky)bar design，testing and applications［M］.Springer New York Dordrecht Heidelberg London，2011:7－17.

［18］李成武，解北京，楊 威.基于HHT法的煤沖擊破壞SHPB測試信號去噪 ［J］.煤炭學報，2012，37(11):1796－1801.

［19］Daubechies I.小波十講［M］.李建平，楊萬年，譯.北京:國防工業出版社，2004:38－40.

［20］付玉凱，李成武，段昌瑞，等.煤體失穩破壞過程中的低頻磁場變化特征研究 ［J］.煤礦開采，2014，19(4):13－17，76.

［21］林 君，項葵葵，朱寶龍，等.MT信號現場處理的實現技術研究［J］.數據采集與處理，1997，12(1):52－55.

［22］李成武，解北京，楊 威.煤沖擊破壞過程中的近距離瞬變磁場變化特征研究 ［J］.巖石力學與工程學報，2012，31(5):973－981.

［23］程 磊，瞿偉廉.基于Hilbert－Huang變換理論的非平穩數據處理［J］.建筑科學與工程學報，2007，24(1):26－30.