基于偏差迭代的干擾源定位算法

2015-08-24 02:53:47侯當云呂偉杰

傳感技術學報 2015年12期

侯當云，呂偉杰

（天津大學電氣與自動化工程學院，天津300072）

基于偏差迭代的干擾源定位算法

侯當云，呂偉杰*

（天津大學電氣與自動化工程學院，天津300072）

針對無線傳感器網絡易受干擾攻擊而導致網絡通信受阻甚至癱瘓等問題，為確定干擾源位置進而消除干擾、保障網絡正常通信，提出了偏差迭代定位算法。在確定初始估計位置后，通過參與定位的三個候選節點的位置信息即可求出干擾源估計位置與實際位置的大致偏差，對不滿足精度要求的初始估計位置進行迭代直到偏差小于規定閾值為止。該算法不依賴網絡本身或者外部設備等復雜的硬件設施和技術支持，對現存方法中存在的定位誤差大、網絡耗能高等問題進行了改善。仿真實驗證明，該算法在不同網絡環境下定位效果均優于現存算法。

無線傳感器網絡；定位；偏差迭代；閾值；仿真

EEACC：7230doi：10.3969/j.issn.1004-1699.2015.12.015

無線傳感器網絡WSNs（Wireless Senor Networks）是由部署在監測區域內大量的廉價微型傳感器，通過無線通信方式形成的一個多跳的自組織網絡［1］。其巨大的發展前景和應用價值已經引起軍事部門、工業界、學術界的廣泛關注，同時，由于無線媒介的開放性、廣播性等本質特征導致網絡可以輕易的受到非法竊聽、篡改消息和拒絕服務等許多安全威脅［2］，因此保證網絡通信的安全性和可靠性變得日益重要。在無線傳感器網絡受到的各種威脅當中，干擾攻擊（jamming）對網絡的危害最大，干擾攻擊的發起者稱之為干擾源（jammer）。干擾攻擊是一種通過占用網絡節點通信信道，使其不能進行正常數據轉發的拒絕服務攻擊，敵人可利用無線網絡的開放性等本質特征，輕易的在網絡中設置干擾。為應對干擾攻擊，傳統方式通過采用直接序列擴頻DSSS（Direct Sequence Spread Spectrum）和跳頻序列擴頻FHSS（Frequency Hopping Spread Spectrum）［3］等方法來增強網絡防御能力從而抵抗干擾對網絡造成的不利影響。但考慮到基于802.11的無線局域網、自組織網絡以及基于802.15.4的無線分布式傳感器網絡在頻寬、能耗以及計算能力方面的受限性［4-6］，并且對物理層的設計不僅復雜而且需要很強的技術支持，使得這些傳統方法在實際應用中并不常用。

為了保證無線網絡通信的可靠性，消除干擾帶來的不利影響，找到干擾源所在的位置變得尤為重要。干擾源位置一旦確定，就可以通過對其進行徹底銷毀或者通過設計路由協議避開被干擾區域從而完全消除干擾攻擊對無線傳感器網絡的影響［7］。

1　相關工作

為了消除干擾對網絡的攻擊，我們首先需要了解各種網絡攻擊模型［8］。其次是網絡對攻擊的檢測問題。本文假設是在固定攻擊模型下，網絡可以準確檢測到干擾激活后進行的，因此不再考慮干擾的檢測階段。最后的關鍵問題是干擾源定位，定位問題是無線傳感器網絡中一個熱點問題。

WSNs定位方法一般分為：基于測距（rangebased）的定位和測距無關（range-free）的定位。基于測距的定位算法主要是通過測量和傳輸節點俘獲的一些物理屬性，如信號強度［9］、到達時間差等信息進行定位。其中具有代表性的是chen等人［10］提出的基于接收信號強度的定位算法，通過測量節點接收信號強度RSS（Received Signal Strength）值，利用RSS與距離之間的關系來估計干擾源位置。但是在Jamming攻擊環境下，被干擾區域的通信已被全部或者部分損壞，并且網絡中存在的多路徑衰退效應使得測量和傳輸準確的RSS值難度大大提高，因此基于測距的定位在實際環境中定位效果差不適宜于干擾定位。

測距無關定位算法則依靠盡可能少的信息，如已知的部分節點位置信息、節點轉發跳數等進行定位，其中經典算法包括純質心定位算法CL（Centriole Localization）及考慮權重的質心定位算法［11］WCL（Weight Centriole Localization），liu等人［12］提出的虛擬力迭代定位法。針對已有算法定位準確性不足，孫言強等人［13］提出了基于幾何覆蓋的干擾攻擊定位算法GCL（Geometry Covering based Localization），找出一個最小包容圓使其能覆蓋所有的邊界節點，則圓心處作為估計干擾源位置。由于幾何算法不依賴網絡本身或其他設備等復雜的測距知識、算法簡單且定位精度高，因此開始成為研究定位問題的主要方向。

結合現有算法的不足之處，本文提出的算法無需任何測距上的先驗知識和硬件設施，把定位中的優化問題抽象成簡單的數學模型，只需參與定位的部分節點自身的位置信息即可求出干擾估計位置和實際位置的大致偏差，簡單可行，同時有效的減少網絡能量的消耗。

2　網絡模型

本節主要介紹參與干擾源定位的網絡模型和攻擊模型。

2.1網絡模型

無線傳感器網絡廣泛應用于軍用、民用，等大規模、大范圍場合，為節約成本提高安放效率傳感器節點由飛機高空隨機撒播。在一定區域撒播下大量節點后，節點會通過自組織的方式相互連通構成網絡。為了表征無線傳感器網絡節點的狀態，對其進行如下假設：①節點的固定性，網絡一旦形成，節點位置固定不變；②位置感知能力，網絡形成后，節點可以準確感知自己所在的位置；③檢測性，可以準確感知到干擾的存在，因此不再考慮干擾的檢測階段。

2.2攻擊模型

恒定干擾通過持續的發送無線電信號來擾亂正常網絡的通信信道，本文主要針對恒定干擾對網絡的影響進行研究。對恒定干擾我們做如下假設：①位置固定，干擾一旦激活，位置固定不變；②傳播模型，以全方位球形輻射模式向網絡持續發送恒定功率的無線電信號，干擾半徑r的大小代表干擾功率的大小。

干擾一旦激活，如圖1所示，網絡節點狀態即被劃分為三種，處在干擾范圍內的節點成為被干擾節點，失去全部通信能力成為網絡的通信“黑洞”；遠離干擾范圍的節點為正常節點，不受干擾影響保持正常通信；其中處于干擾范圍邊緣的點成為邊界節點，這類節點通信并沒有被完全破壞，保持部分通信能力，可以向網絡外部傳輸其俘獲的各種信息，成為定位干擾源的關鍵節點。

3　本文算法分析

3.1問題分析

干擾激活后可利用網絡拓撲變化形成的邊界節點來進行干擾源的定位，這是因為邊界節點處于干擾范圍的邊緣使得邊界節點的通信能力并沒有被完全破壞，可向外部傳輸其準確的位置信息。

我們利用質心法求出干擾源初始估計位置，確定初始估計位置后，干擾源估計位置與實際位置之間可能存在偏差，因此利用偏差迭代定位算法確定干擾源的最終估計位置。我們設定偏差閾值為0.001，即橫縱坐標的偏差均小于0.001，利用最小二乘法求出干擾源估計位置與實際位置的大致偏差，若精度不滿足要求，則將校正后的坐標代替估計坐標，進行下一步的矯正，直到偏差小于規定閾值迭代結束。得到最終干擾源估計位置，此時偏差滿足閾值要求，最接近干擾源的真實位置。

3.2偏差迭代定位算法

設干擾源J的實際位置是（x0,y0），初始估計位置（x?0,y?0），邊界節點位置為（xi,yi）。可將干擾源初始估計位置與實際位置偏移表示為（Δx0,Δy0），J到邊界節點的距離為ri，為了計算J的位置，定義了一個最大似然估計函數f，并選擇這個函數的一個局部最小值，設f=ri-r?i。

式中：實際距離

估計距離

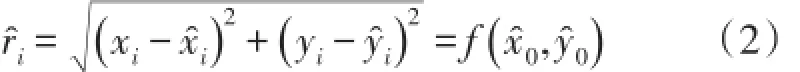
如上所述，J的真實位置可由近似分量和增量兩部分表示：

因此有：

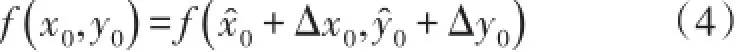
按泰勒級數對式（4）右邊函數展開得：

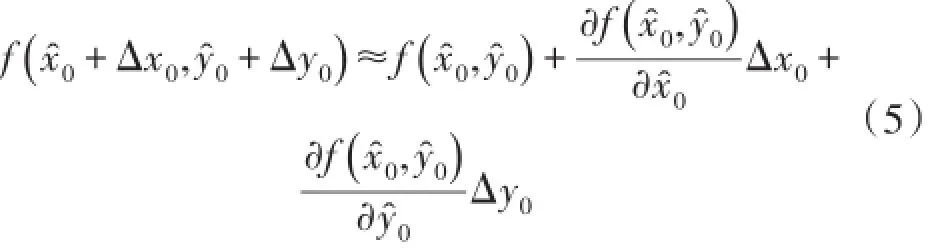
為消除非線性，展開式（5）中消去了一階偏導數之后的各項，偏導數計算為：

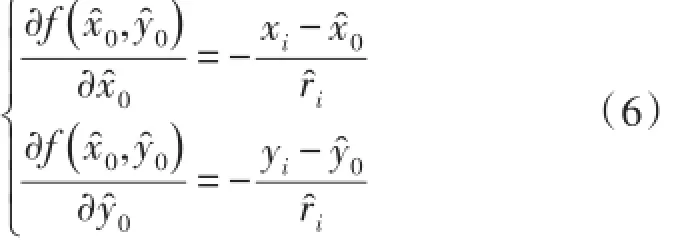
把式（3）～（6）帶入式（2）中得：

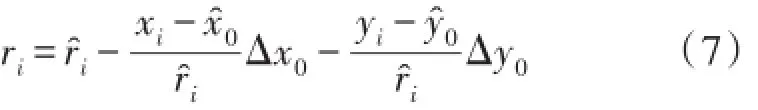
為簡化公式（7），引入下述變量：

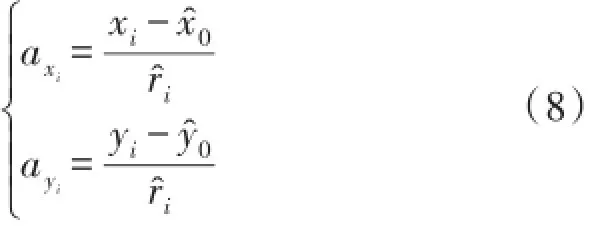
這樣式（7）可表示為：

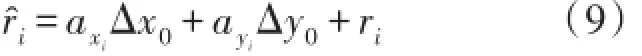
在式（9）中等號左邊為已知量，右邊為未知量，設：

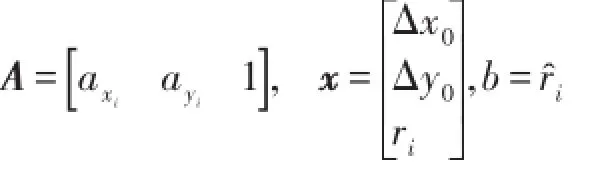
式（9）可表示為：

由此，得出：

因為在最大似然估計函數線性化過程中存在誤差，解得的偏移向量為干擾源估計位置與實際位置的大概偏差。參與最后求解的方程組中有三個未知量，因此至少需要三個方程組即三個邊界節點的位置信息，可在網絡拓撲變化后的邊界節點中選擇。

4　算法性能分析

我們使用仿真工具搭建一個100 m×100 m仿真平臺，在該區域隨機撒播節點。節點通信半徑設定為20 m，每個節點裝有全向天線可以與自己通信范圍內的所有鄰居節點進行通信。將干擾放置在仿真平臺的中心。每次隨機撒播完節點在特定的干擾場景下調用這四種定位算法，把本文提出的算法和已有算法CL，WCL以及GCL進行比較，在100次隨機試驗中評估算法的定位效果。

4.1評價指標

干擾源估計位置和真實位置之間的歐氏距離定義為單次定位誤差，如式（12）所示。把單次定位誤差相加求平均，即為平均定位誤差，如式（13）所示。

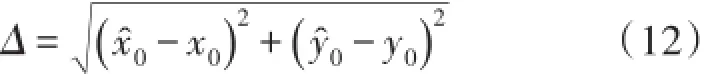
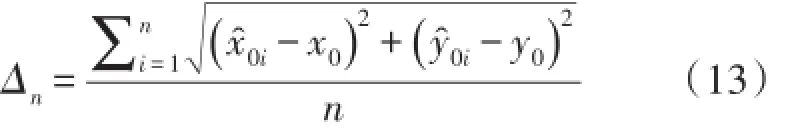
單次定位誤差由于采樣少而存在隨機性，平均定位誤差更能代表算法的優劣。為了保證評估效果的準確性，我們把平均定位誤差指標作為評價的主要指標。這也是在現存定位方法中首次提出采用平均定位誤差作為評價指標。

4.2實驗分析

4.2.1干擾源功率對定位精度的影響

節點密度相同，調整干擾功率：在100 m×100 m區域內隨機撒播200個節點（100 m×100 m，N= 200），使干擾半徑r分別為20 m、30 m和40 m。每種算法隨機運行100次，仿真結果如圖2所示。

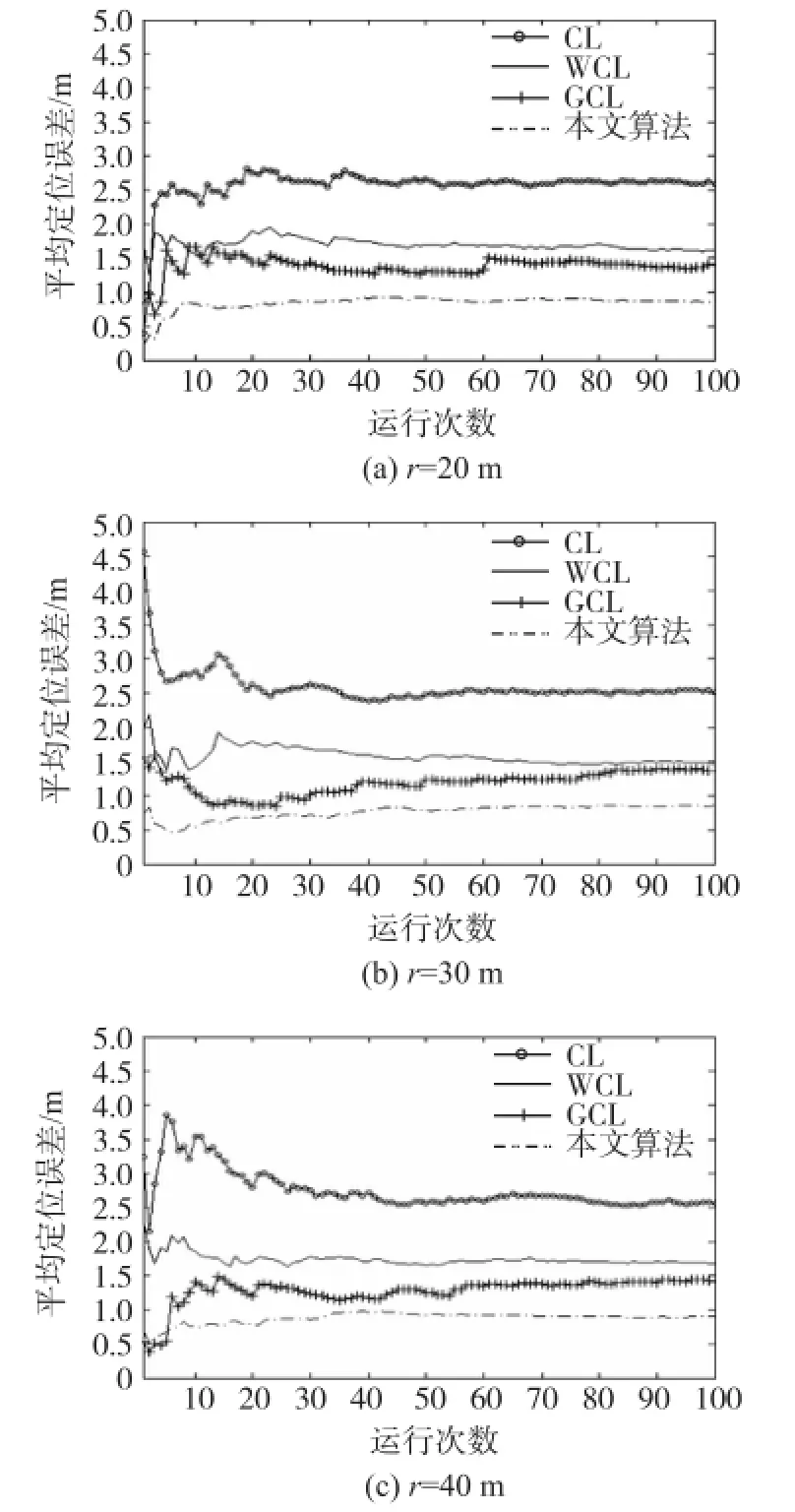
圖2　R干擾功率對算法精度的影響（N=200）

在功率變化的三種情況下CL定位算法定位效果最差，本文提出的定位效果最好。當干擾功率增大時，四種算法的平均定位誤差都有減小的趨勢，說明四種算法的定位精度都與干擾功率大小有關，這是因為當干擾功率增大時，被干擾節點和邊界節點的數目也相應增加，參與定位的候選節點數增加，從而在一定程度上使定位誤差減小。通過仿真圖的曲線波動情況可以看出，在不同的干擾功率情況下本文提出的算法曲線平穩、波動最小，因而定位精度最高且適應性最強，這是傳統單次定位誤差所無法評估的。

4.2.2節點密度對定位精度的影響

干擾功率一定，調整節點的密度：在100×100區域隨機撒播100，150，200，250個節點，干擾激活后干擾半徑保持30 m不變。每種情況下四種算法隨機運行100次，仿真結果如圖3和圖2中（2）所示。在不同的節點密度下，本文提出的算法定位精度仍然最好。并且隨著節點的密度增大，四種算法的定位誤差都有減小的趨勢，這是由于當節點密度增大時，被干擾節點和邊界節點的數目增加并且參與定位的候選節點分布區域更趨近于圓，從而使四種算法的定位精度都有所提升。由此可以看出節點密度越大定位誤差越小，反之則定位誤差越大。從四種算法的平均定位誤差曲線圖可以看出本文算法曲線平穩震蕩小，表明隨機定位效果好。

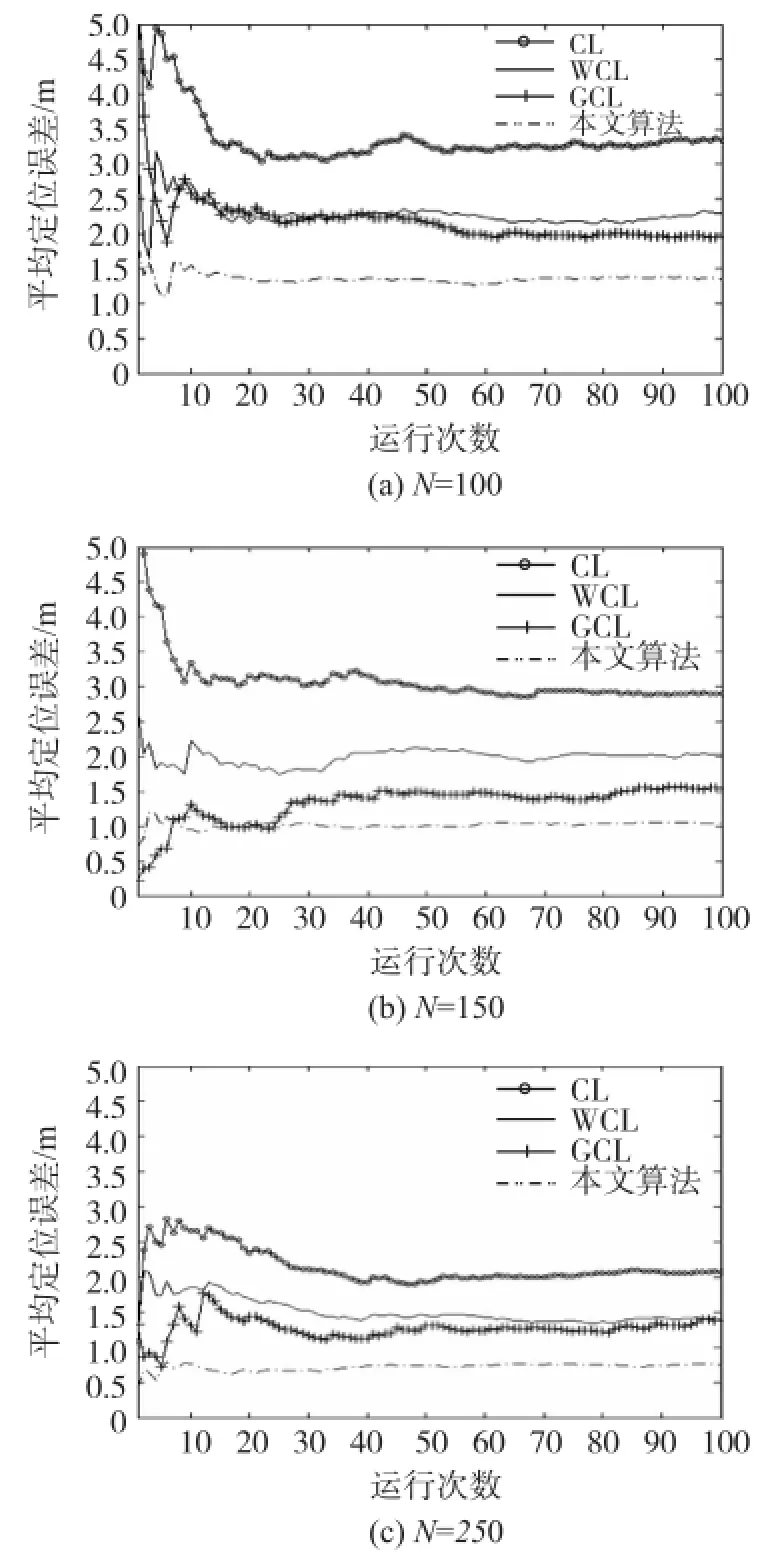
圖3　R節點密度對算法精度的影響（r=30 m）

4.3機理分析

在實際網絡環境中，當干擾源位置處于網絡邊緣，或者節點隨機撒播以及傳播過程中功率損耗不同造成的各方向上邊界節點密度不均勻時，形成的邊界節點將不再包圍干擾源或者造成不同方向邊界節點分布密度差異很大，因而CL、WCL和GCL的定位誤差都將大大增加。但是本文提出的算法在幾何定位的基礎上進行優化，只要確定的邊界節點的絕對位置信息即可縮小定位誤差，而對整體的邊界節點相對位置信息無任何附加要求，因而即使干擾源位置邊緣化或邊界節點密度不均勻時，依然可以達到良好定位效果。

5　結語

由于無線傳感器網絡的本質特征導致網絡易受干擾攻擊而導致通信失敗或網絡癱瘓，為消除干擾保證網絡正常通信，我們對干擾源定位問題進行了進一步的研究，在固定網絡模型和干擾模型的基礎上，把定位問題轉化成簡單的數學優化問題。通過仿真驗證，本文提出的算法比現存幾種算法定位精度顯著提高。但是對于無線傳感器網絡來說，其網絡模型和干擾攻擊模型是多種多樣的，在以后的研究中，我們可以對移動的干擾模型和聯合干擾模型的定位問題進行進一步的探索。

［1］趙仕俊，唐懿芳.無線傳感器網絡［M］.北京：科學出版社，2013：1-3.

［2］畢俊蕾，李致遠.無線傳感器網絡安全路由協議研究［J］.計算機安全，2009（11）：35-38.

［3］Shiu Y S，Chang S Y，Wu H C，et al.Physical Layer Security in Wireless Networks：A Tutorial［J］.Wireless Communications，IEEE，2011，18（2）：66-74.

［4］Ian F Akyildiz，Su Weilian，Yogesh Sankarasubramaniam，et al.A Survey on Sensor Networks［J］.IEEE Communications Magazine，2002，40（8）：102-114.

［5］Zhou Yun，Fang Yuguang，Zhang Yanchao.Securing Wireless Sensor Networks：A Survey［J］.Communications Surveys and Tutorials，IEEE，2008，10（3）：6-28.

［6］Loay Abusalah，Ashfaq Khokhar，Mohsen Guizani.A Survey of Secure Mobile Ad Hoc Routing Protocols［J］.Communications Surveys and Tutorials，IEEE，2008，10（4）：78-93.

［7］聶云峰，王長勝，陳崇毅.一種空間查詢高效的無線傳感網絡路由協議［J］.傳感技術學報，2015，28（5）：744-751.

［8］Konstantinos Pelechrinis，Marios Iliofotou，Srikanth V Krishnamurthy.Denial of Service Attacks in Wireless Networks：The Case of Jammers［J］.Communications Surveys and Tutorials，IEEE，2011，13（2）：245-257.

［9］楊文鉑，邢鵬康，劉彥華.一種基于自適應RSSI測距模型的無線傳感器網絡定位方法［J］.傳感技術學報，2015，28（1）：137-141.

［10］Chen Yingying，John-Austen Francisco，Wade Trappe.A Practical Approach To Landmark Deployment for Indoor Localization［C］//Sensor and Ad Hoc Communications and Networks，2006. SECON'06.2006 3rd Annual IEEE Communications Society on. IEEE，2006，1：365-373.

［11］Blumenthal J，Grossmann R，Golatowski F，et al.Weighted Centroid Localization in Zigbee-Based Sensor Networks［J］.Intelligent Signal Processing，2007.WISP 2007.IEEE International Symposium on.IEEE，2007：1-6.

［12］Liu Zhenhua，Xu Wenyuan，Chen Yingying，et al.Localizing Jammers in Wireless Networks［C］//Pervasive Computing and Communications，2009.PerCom 2009.IEEE International Conference on. IEEE，2009：1-6.

［13］孫言強，王曉東，周興銘.無線傳感器網絡中基于幾何覆蓋的Jamming攻擊定位算法［J］.通信學報，2010，31（11）：10-16.

Based on the Deviation of Iterative Algorithm in Jammer Localization

HOU Dangyun，Lü Weijie*
（School of Electrical Engineering and Automation，Tianjin University，Tianjin 3000072，China）

Wireless sensor networks communication is susceptible to jamming attacks，which would make the network communication blocked or even palsied.In order to localize the position of the jammer and then eliminate it to guarantee the normal communication，we develop a novel algorithm，deviation of iterative localization.After determining the initial estimate position，we calculate the deviation between the estimate position and the actual position through the position of three candidate nodes.If the deviation did not meet the accuracy requirement，iterated until it less than a specified threshold.The algorithm does not depend on the network complex hardware facilities or external device support.The problems of present methods about lager positioning error，higher energy consumption and the like have been improved.Simulation shows that our algorithm under the different network environments outperforms existing algorithms.

wireless senor networks；localization；deviation of iterative；threshold；simulation