應用Lagrange方程研究剛彈耦合動力學
梁立孚,宋海燕,郭慶勇
(哈爾濱工程大學航天與建筑工程學院,黑龍江哈爾濱150001)
從十八世紀開始,在力學發展史上出現了與牛頓的矢量力學并駕齊驅的另一力學體系,即Lagrange于1788年在巴黎正式出版的不朽名著《Mecanique Analytique(分析力學)》[1]。這個體系的特點是對能量與功的分析代替對力與力矩的分析。1834年和1843年W.R.Hamilton建立了Hamilton原理和正則方程,把分析力學推進一步[2]。
如何將經典分析動力學應用于連續介質力學的問題,一直是各國學者關注的研究課題,經過200多年的努力,取得豐碩的研究成果。由這些研究成果明確地反映出,應用Hamilton原理的論述很多,而應用 Lagrange方程的論述較少。這是因為在經典分析動力學中,Lagrange方程式是以離散的質點和質點系為對象建立的,如何應用于連續介質力學,仍然是國內外學者不斷探索的重要課題[3-7]。
通過多年的研究,積累了不少成功的和失敗的經驗,經驗告訴我們,在一定的意義上說,Lagrange方程和Hamilton原理都涉及變分學,Lagrange本人又是變分學的奠基人之一,從變分學的基本理論研究做起,或許是一條可行的途徑。本文作者提出變分的逆運算變積概念,建立了變積方法,得到錢偉長院士的親自推薦[8]。應用變積方法,與胡海昌院士一起,建立了一般力學三類變量的廣義變分原理[9]。劉高聯院士也充分肯定了變積方法[10]。這些研究使得微積分學中的積分、微分和導數在變分學中都有了對應的概念——變積、變分和變導,從而初步地將變分學擴充為變積分學。本文應用變導的概念和運算法則,通過研究Lagrange方程中的求導的性質,逐步地將Lagrange方程應用于彈性動力學,進而應用于剛彈耦合動力學。應用Lagrange方程,建立了剛彈耦合動力學的控制方程。
1 Lagrange方程中的導數的性質
為了說明這個問題,首先,明確變導的概念。
設有定積分形式的泛函:

自變函數為y(x),自變量為x。對式(1)進行變分運算可得
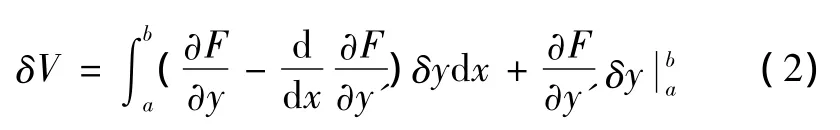
由于δy任意性,式(2)可以變換為

在微分學中,函數的微分表示為dy,自變量的微分表示為dx,微商表示為又稱導數。在變分學中,泛函的變分表示為δV,可變函數的變分表示為δy,變商表示為又稱變導。
接下來,分析Lagrange方程中的導數的性質。經典分析動力學中的Lagrange方程表示為
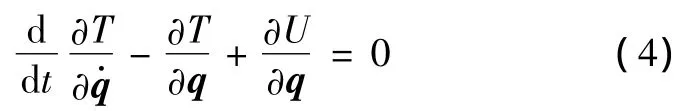
其中,q=q(t)為廣義坐標,一般分析動力學中均把其處理為廣義坐標列陣[q1(t)q2(t)q3(t)…qi(t)…qn(t)]T,i=1,2,3,…,i,…,n。在變分學中,基本上存在三級變量—自變量、可變函數和泛函。簡單函數和泛函的區別在于:簡單函數是自變量的函數,而泛函是可變函數的函數,獨立自主地變化的可變函數稱為自變函數。明確了變分學中的三級變量,對區分微積分中的導數和變積分學中的變導很有幫助。對自變量求導為微積分中的導數,而對可變函數的求導則為變積分中的變導。
這里指出,Lagrange J.L.已經注意到微分符號用“d”和變分符號用“δ”,而且應用了符號中的對時間t求導在文獻[1]中,Lagrange方程表示為

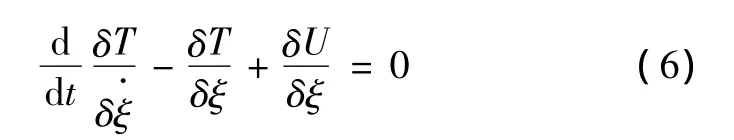
進一步,將變量ξ變換為q則有式(4)。
變積分學中的變導和微積分學中的導數的運算法則,有時相同、有時不同,這類問題,在后面研究具體問題時可以明顯的表達出來。
2 Lagrange方程應用于彈性動力學
彈性動力學的動能可以表示為

彈性動力學的勢能可以表示為

位移邊界條件為

其中,u為位移,為邊界位移,a為剛度系數,t為時間,ρ為物質密度,?為Hamilton算子,f為單位體積力,T為單位面積力,V為體積,Sσ為應力邊界面,Su為位移邊界面。
Lagrange方程表示為
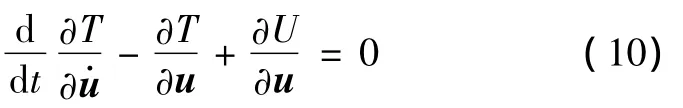
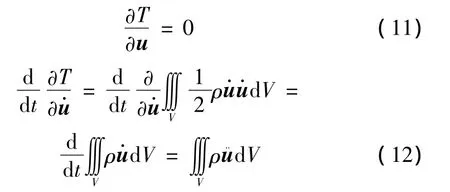
可見,這里對動能求變導的運算法則與微積分中求導數的法則相同。勢能的變導項的推導較為復雜,與微積分中求導數的法則不盡相同:

由于

應用Green定理

將式(16)和式(9)代入式(15),然后將式(15)代入式(14),則得
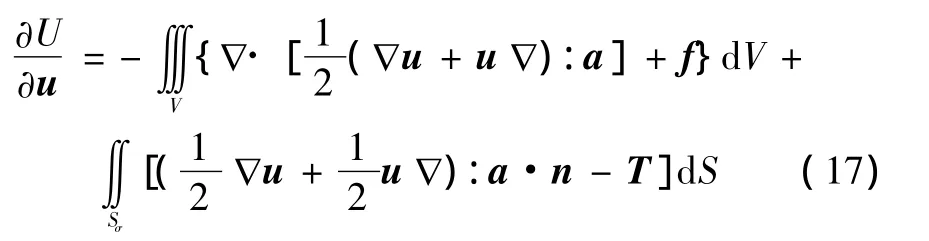
將相關各式代入Lagrange方程,可得

寫成微分形式,可得彈性動力學控制方程的一種表達形式
此外,學生作為案例教學的最大受益方,其教學效果與所選擇的案例類型間存在著密切聯系,而實際教學過程中學生能力鍛煉程度及綜合素質提升程度,無法脫離詳細的分析、調查、測試及評價等環節的支持。按評價方法類型,案例教學效果評價方法可分為考試測試、調查問卷、一對一訪談及教學過程客觀評價。
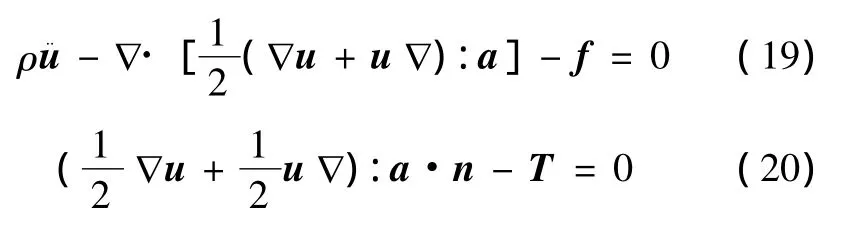
位移邊界條件為式(9)。
3 Lagrange方程應用于剛彈耦合動力學
以飛行器為例,同樣是一個飛行器,當研究它的軌道動力學時可以簡化為質點模型,當研究它的姿態動力學時可以簡化為剛體模型,當研究它的機械振動和動力響應時可以簡化為彈性體模型,當對它的軌道、姿態、機械振動和動力響應以及它們之間的耦合效應進行全面研究時,則簡化為剛彈耦合模型。
3.1 剛彈耦合動力學中的動能
因為這類問題的變量多、公式復雜,以下采用實體張量符號書寫。對于所研究的物體,如圖1所示。
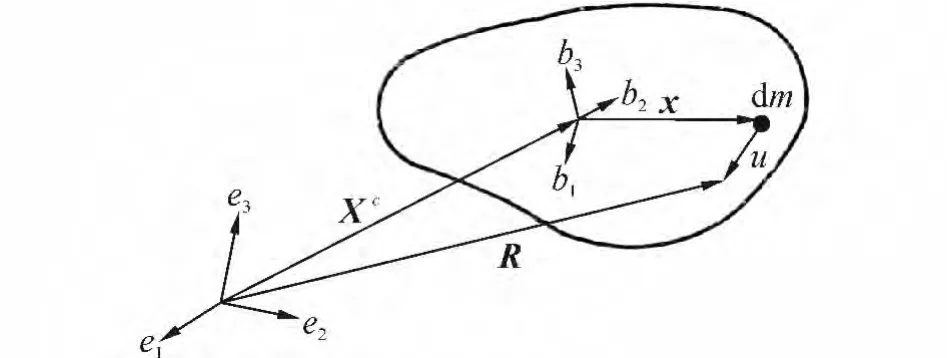
圖1 e坐標系和b坐標系Fig.1 e coordinate system and b coordinate system
假設圖中的e坐標系為慣性坐標系,b坐標系為連體坐標系(一般為非慣性坐標系)。物體上任意一點的總矢徑為R=Xc+x+u,其中,Xc為質心矢徑,x是把物體視為剛體時由質心到剛體中任意一點的矢徑,u為把物體視為彈性體時該點的彈性位移,設Xc+x=X。
將物體視為剛體時的轉角為θ,可以認為是偽坐標。可見,對于剛彈耦合體,除了剛體速度外,還有變形體速度(其中,×表示矢量的叉乘符號),這里應當注意到變形體速度與剛體轉動的交聯。應用Coriolis轉動定理,注意到的力學模型中,矢量x的模為剛體質心到任意點的距離,而剛體中任意兩點間的距離都是常量,因此,故有,總之
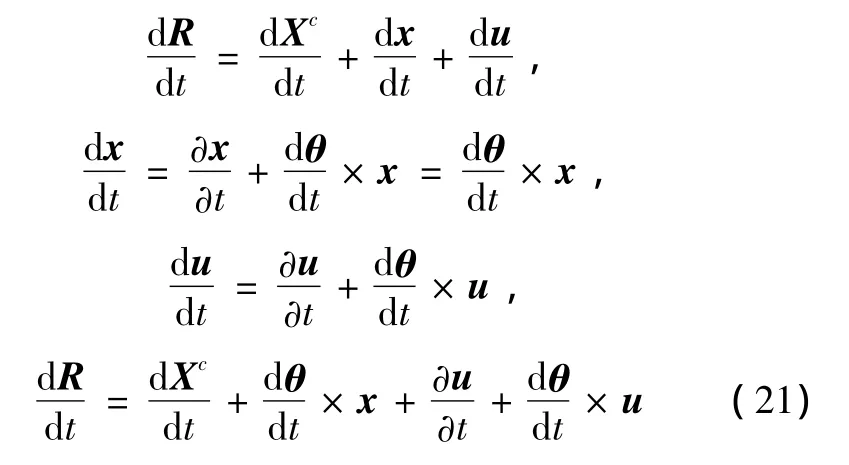
由于

因此,剛彈耦合動力學中的動能可以表示為

或者
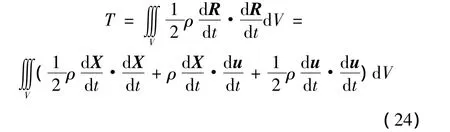
因為[11]
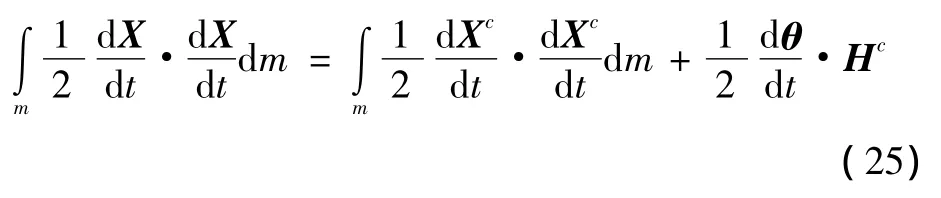
所以,剛彈耦合動力學中的動能又可以寫為
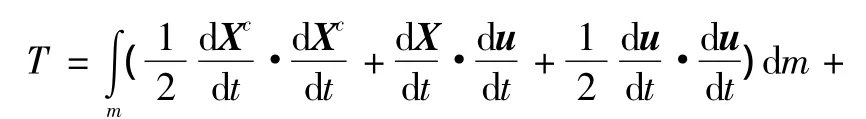
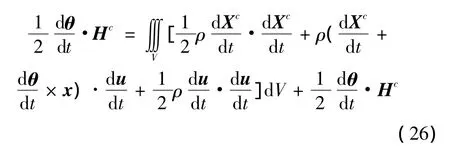
式中:Hc為對質心的動量矩,J為對質心的轉動慣量;m為質量。
3.2 剛彈耦合動力學中的勢能
參照彈性力學中的做法,剛彈耦合動力學中的勢能一部分為
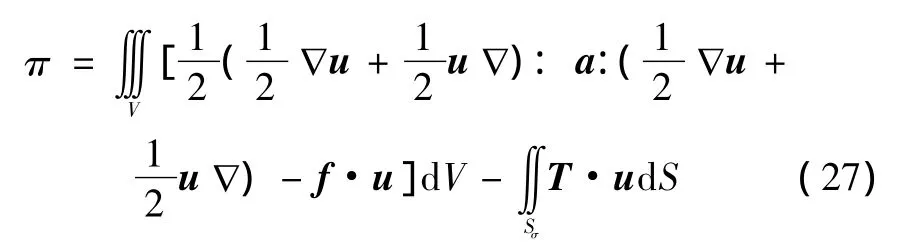
位移邊界條件為

剛彈耦合動力學中的勢能另一部分為由于作用于剛體的外力主矢和外力主矩引起的勢能

兩部分勢能的和為

3.3 應用Lagrange方程建立剛彈耦合動力學的控制方程
Lagrange方程為

推導計算Lagrange方程中的有關動能的各項:



推導計算Lagrange方程中的有關勢能的各項:
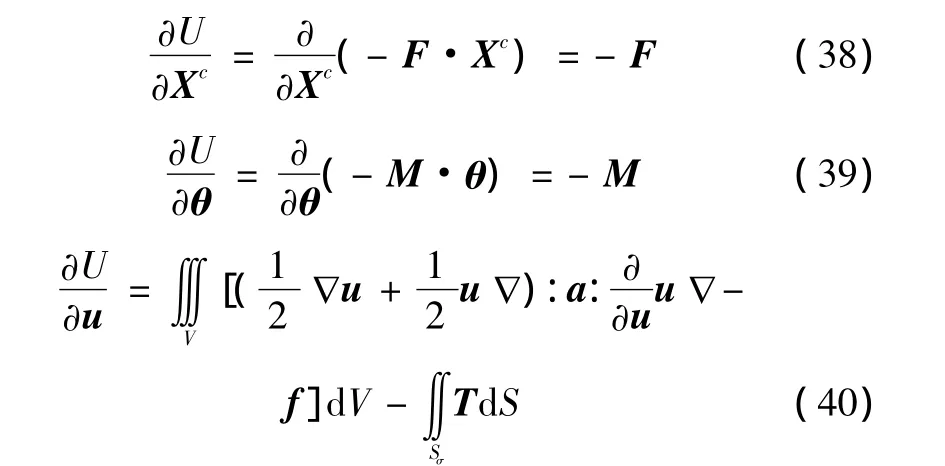
應用Green定理

將式(41)代入式(40),考慮到邊界條件(28),可得
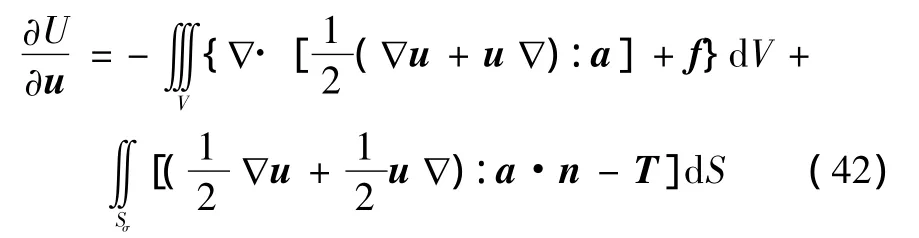
將以上的推導結果代入Lagrange方程中,可得
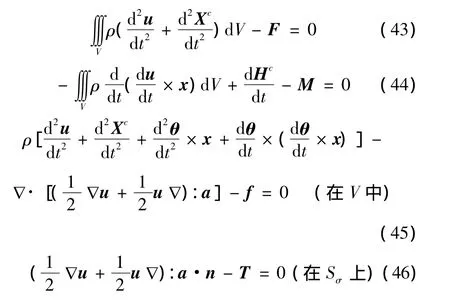
這就是剛彈耦合動力學的控制方程。
4 結束語
本文應用變導的概念和運算法則,研究了 Lagrange方程中的求導的性質,并成功地將Lagrange方程應用于彈性動力學。根據功能原理和能量守恒定律,應用Lagrange方程,建立了剛彈耦合動力學的控制方程。應用Lagrange方程解決了多個彈性動力學和剛彈耦合動力學的理論與應用問題。
[1]LAGRANGE J L.Analytical mechanics[M].Dordrecht:Kluwer Academic Publishers Group,1997:169-183.
[2]HAMILTON W R.On a general method in dynamics[J].Philosophical Transactions of the Royal Society,1834(Part I):247-308,1835(Part II):95-144.
[3]汪家訸.分析動力學[M].北京:高等教育出版社,1958:426-487.
[4]沈惠川.彈性力學的Lagrange形式:用Routh方法建立彈性有限變形問題的基本方程[J].數學物理學報,1998,18(1):78-88.SHEN Huichuan.Lagrange formalism of elasticity:building the basic equationson finite-deformation problemsby Routh's method[J].Acta Mathematica Scientia,1998,18(1):78-88.
[5]繆炳祺,曲廣吉,夏邃勤,等.柔性航天器動力學建模的偽坐標形式Lagrange方程[J].中國空間科學技術,2003(2):1-5,57.MIAO Bingqi,QU Guangji,XIA Suiqin,et al.Lagrange's equations in quasicoordinates for dynamics modeling of flexible spacecraft[J].Chinese Space Science and Technology,2003(2):1-5,57.
[6]SOUCHET R .Continuum mechanics and Lagrange equations with generalised coordinates[J].International Journal of Engineering Science,2014,76:27-33.
[7]HERBERT G.,CHARLES P,JOHN S.Classical Mechanics[M].3rd ed.Beijing:Higher Education Press,2005:449-600.
[8]LIANG Lifu,SHI Zhifei.On the inverse problem in calculus of variations[J].Applied Mathematics and Mechanics,1994,15(9):815-830.
[9]LIANG Lifu,HU Haichang.Generalized variational principle of three kinds of variables in general mechanics[J].Science in China(A),2001,44(6):770-776.
[10]梁立孚.變分原理及其應用[M].哈爾濱:哈爾濱工程大學出版社,2005:序言1-2.
[11]LIANG Lifu,SONG Haiyan.Non-linear and non-conservative quasi-variational principle of flexible body dynamics and application in spacecraft dynamics[J].Science China Physics,Mechanics and Astronomy,2013,56(11):2192-2199.

