顆粒內部毛細凝聚對氣體有效擴散系數的影響

羅文，吳思操，劉鵬，程振民，周志明，方云進

（華東理工大學化學工程聯合國家重點實驗室，上海 200237）

引 言

有效擴散系數是氣固相催化反應中的一個重要模型參數，反映了氣體在催化劑孔道中傳遞速率 的快慢，測量有效擴散系數可以為催化劑的制備和尋求最佳反應條件提供依據。在固定床反應器中進行加氫反應時，一定條件下可凝性蒸氣會在多孔催化劑內發生毛細凝聚，從而使催化劑處于內部潤濕 狀態[1-2]。多孔催化劑內毛細冷凝物的存在會阻礙氣體在催化劑孔道內的擴散，降低反應速率。

影響氣體有效擴散系數的因素非常多，例如溫度、壓力、氣體分子的大小、催化劑的孔徑分布、孔道結構和孔網絡特性等。Zheng 等[3-4]提出氣體在分形多孔介質中的擴散模型，推導出有效擴散系數是關于分形維數、曲節因子、孔隙率和孔徑的函數。Mezedur 等[5]建立了O2-N2雙組分的二維網絡模型，得到不同孔徑大小顆粒中的有效擴散系數，將有效擴散系數劃分為三段曲線，指出各段內的擴散機理均不同。Mu 等[6]用三維網絡模型研究了隨機孔材料中的氣體擴散，提出了主體擴散系數、努森擴散系數與孔徑大小的關系式，發現當孔徑小于1 μm 時，有效擴散系數受孔徑影響很大。汪叔雄等[7]用穩態法和脈沖響應法測定了氣體在隨機孔和平行孔結構的多孔催化劑內有效擴散系數，結果表明對于隨機孔結構的催化劑兩種方法測定結果接近，而對具有平行孔結構的催化劑用脈沖響應法測定更加合適。王桂榮等[8]利用新型擴散池測定了多孔催化劑中的有效擴散系數，表明曲節因子是催化劑的一個結構參數，它不隨溫度、擴散組分種類和組分濃度變化而變化，而有效擴散系數隨著溫度升高而增大。

毛細凝聚是中孔材料的一個吸附特征，其對氣體在催化劑孔內有效擴散系數影響很大。以往研究者大多主要研究吸附等溫線與孔結構之間的關系[9-11]，而針對反應體系的研究較少。這方面的工作主要有：苯和環己烷在催化劑上吸附行為的比較[12]，蒸氣冷凝對加氫反應速率滯后環形狀的研究[13]，孔網絡結構對加氫反應速率滯后環大小的影響[14]，加氫速率與內部潤濕分率之間的關系[15]。但迄今為止，采用實驗測定多孔催化劑內發生毛細凝聚現象時氣體有效擴散系數的研究未見報道，而這又是建立內部潤濕分率與有效擴散系數之間關系所必需的。本文旨在采用單顆粒Wicke-Kallenbath 穩態擴散池，測量環己烷在多孔催化劑孔道內發生毛細冷凝時氫氣在催化劑孔內的有效擴散系數，并探討催化劑孔內發生毛細凝聚時有效擴散系數與溫度、壓力以及內部潤濕分率之間的關系。

1 實驗部分

1.1 催化劑的孔徑分布

多孔催化劑CuO/ZnO/γ-Al2O3在1～10 nm范圍內的孔徑分布采用Micromeritics 公司生產的ASAP 2020 型吸附儀以液氮為吸附介質在77.3 K 溫度下 測定。催化劑在0.01～188.62 μm 范圍的孔徑分布測定采用Quantachrome 公司生產的PoreMaster-33全自動壓汞儀完成。孔徑分布測定結果如圖1所示。

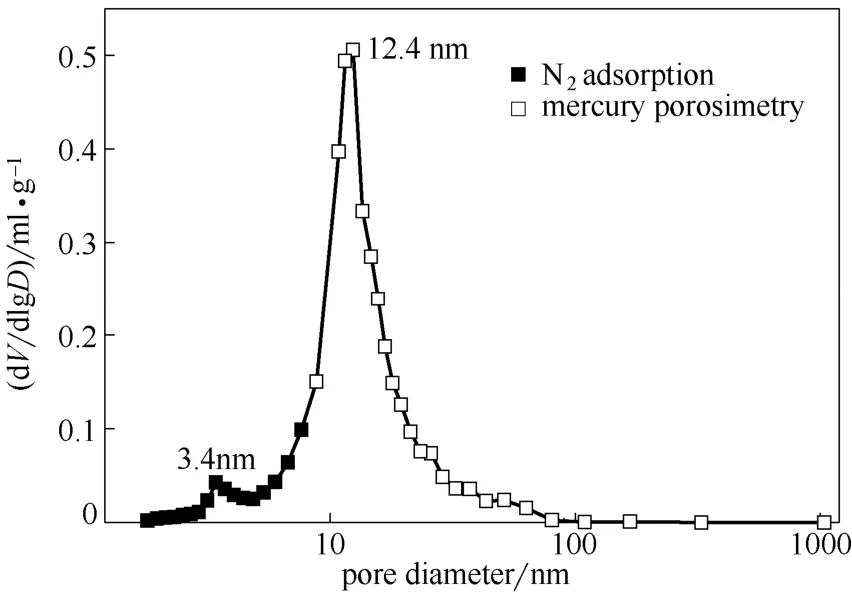
圖1 催化劑的孔徑分布Fig.1 Pore diameter distribution of CuO/ZnO/γ-Al2O3

所測得孔徑分布曲線近似服從對數正態分布

式中，r為孔半徑；v為單位質量催化劑所具有的孔體積；為平均孔半徑；σ為表面張力。根據式(1)對實驗數據進行非線性回歸，得到：v=0.456 cm3·g-1，σ=0.392 mN·m-1，=5.01 nm。

1.2 吸附實驗

采用重量法和逐步增加環己烷流量至某最大值而后逐步降低回到初始點的方法研究在373～413 K 及0.4～1.0 MPa 條件下環己烷在催化劑上的吸附行為。每個環己烷流量值都有其對應的相對壓力。實驗操作條件與有效擴散系數的測量實驗條件相同，便于分析其吸附特征和求解每個有效擴散系數對應的內部潤失分率。實驗流程及操作方法詳見文獻[12]。

1.3 有效擴散系數的測量實驗

采用單顆粒定常態法（5 mm×5 mm 圓柱形顆粒）測定環己烷蒸氣在催化劑孔道內發生毛細凝聚時氫氣在多孔催化劑中的有效擴散系數，實驗流程如圖2所示。高純氫經減壓閥減壓、質量流量計（北京七星D07 質量流量控制器）調節流量后經預熱至實驗溫度后通入擴散池下腔室。高純氮經減壓閥、質量流量計（北京七星D07 質量流量控制器）與從微量計量泵（Eldex ReciPro Series 2000）注入的環己烷液體混合，預熱至實驗溫度后通入擴散池上腔室。部分氫氣由擴散池下腔室擴散至上腔室，與擴散池上腔室中的氮氣、環己烷蒸氣混合后經過冷凝器、氣液分離器、背壓閥、氣相色譜、尾氣吸收瓶后排空。用氣相色譜（天普GC900C）分析尾氣中氫氣含量，每隔15 min 測定一次，待前后兩次結果相同時，認為氫氣在擴散池中的擴散達到穩態，記錄此時的數據。

圖2 氫氣有效擴散系數測量的實驗流程Fig.2 Flow diagram for determination of effective diffusivity of hydrogen

2 理論部分

2.1 臨界滯后孔半徑

蒸氣在催化劑孔道內的吸附主要分為3 個步驟：①單分子層吸附；②多分子層吸附；③毛細冷凝。

單分子層的厚度tm可用下式計算

式中，S表示分子的投影面積，NA是Avogadro常數。

多分子層的厚度t由Halsey 公式計算

蒸氣在孔道內的毛細冷凝是逐步進行的，它是在多分子層形成的基礎上當毛細孔內核半徑等于或者小于臨界半徑rc時，蒸氣在分子間作用力下發生的相態轉化。毛細孔內核半徑rc由Kelvin 方程計算得到

式中，Rg是理想氣體常數。由此可見，蒸發和冷凝并不是嚴格可逆的，給定壓力下兩種現象發生時的內核半徑不相同，這是產生滯后環的根本原因。

當吸附物質在孔表面形成多分子層后，在給定溫度和相對壓力P/P0下有一個臨界滯后孔半徑rch。孔半徑等于或小于rch的孔都將發生毛細冷凝而充滿液體，即處于“潤濕”狀態；孔半徑大于rch的孔均發生多分子層吸附，但不會發生毛細冷凝[16]。

臨界滯后孔半徑rch與多分子層厚度t和內核半徑rc之間關系如下

2.2 內部潤濕分率

當達到Kelvin 方程滿足的條件，蒸氣將在催化劑孔內多分子層上發生毛細凝聚。Cheng 等[17]基于吸附/脫附實驗提出了計算內部潤濕分率fw的方法

式中，V表示可凝性物質在催化劑孔內的吸附，V0表示催化劑的孔體積，VS表示吸附等溫線滯后環起點對應的吸附量。

2.3 有效擴散系數

氣體在催化劑毛細孔內的擴散主要有分子擴散和努森擴散兩種形式。當孔道直徑d與氣體分子平均自由程λ滿足d/λ≥100 時，擴散系數是溫度和壓力的函數，不受孔壁影響，主要由分子擴散控制；當d/λ≤1 時，氣體分子與孔壁碰撞要比分子之間碰撞頻繁，擴散系數不受壓力影響，主要由努森擴散控制。雙組分體系的分子擴散系數DAB可用Chapman-Enskog 公式計算

式中，碰撞積分 ABΩ是的函數，k是Boltzmann 常數，ABε是Lennard-Jones 勢能函數。

Knudsen 擴散系數DK可由分子運動平均速度推導得到

根據 “塵氣”模型[18]，可認為氣體在圓柱孔內的擴散是一個串聯過程，總阻力是分子擴散阻力和努森擴散阻力之和，故綜合擴散系數D可表示為

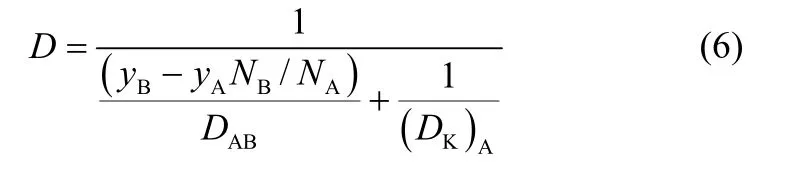
式中，yA表示A 組分的摩爾分數，BA/N N=(MA/MB)0.5。

對于催化劑內部有效擴散系數的計算，Johnson等[19]提出了比較切合實際的交聯孔模型，該模型通過將單孔綜合擴散系數沿孔徑分布積分，計算氣體在整個催化劑內的有效擴散系數

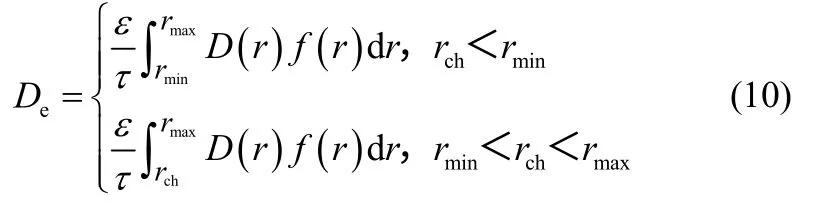
將式(1)和式(9)代入式(10)，可求得發生毛細凝聚時的有效擴散系數。式中rmin、rmax分別是吸附儀測得的最小孔半徑和壓汞儀測得的最大孔半徑。本文取rmin=1 nm，rmax=50 nm。當rmin＜rch＜rmax時，理論上孔半徑小于rch全部毛細孔均可以發生毛細凝聚，由于氣體在液相中的擴散系數遠小于在氣相中的擴散系數，故積分范圍只取大于rch部分。

2.4 有效擴散系數與內部潤濕分率的關系

Hessari 等[20]提出處于內部潤濕狀態時反應速率是“全干”和“全濕”兩個狀態下反應速率的線性加和。有效擴散系數是內部潤濕分率的函數，由于催化劑存在孔徑分布，潤濕率分布不均，二者之間為非線性關系，可采用參數擬合的方式建立綜合有效擴散系數De,t與內部潤濕分率fw、“全干”狀態時的有效擴散系數De,g、“全濕”狀態時的有效擴散系數De,l之間的關系[13]，形式如下

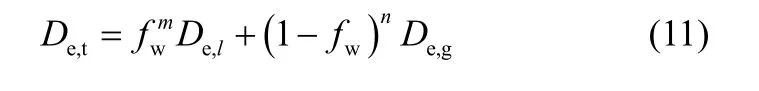
式中，m、n是待確定的參數，由實驗結果來確定。

3 實驗結果與討論

3.1 吸附等溫線

3 種操作條件下的吸附等溫線如圖3所示。當操作溫度為373、393 和413 K 時，吸附等溫線的滯后環起始點對應的環己烷蒸氣相對壓力分別為0.42、0.50、0.60。可見隨著吸附溫度的升高，滯后環朝著相對壓力增大的方向移動，并且寬度逐漸變窄。此外，每種操作條件下，從不同最大相對壓力 值降低回到初始點，都有一個對應的滯后環，因此在吸附曲線上出現多重滯后環。

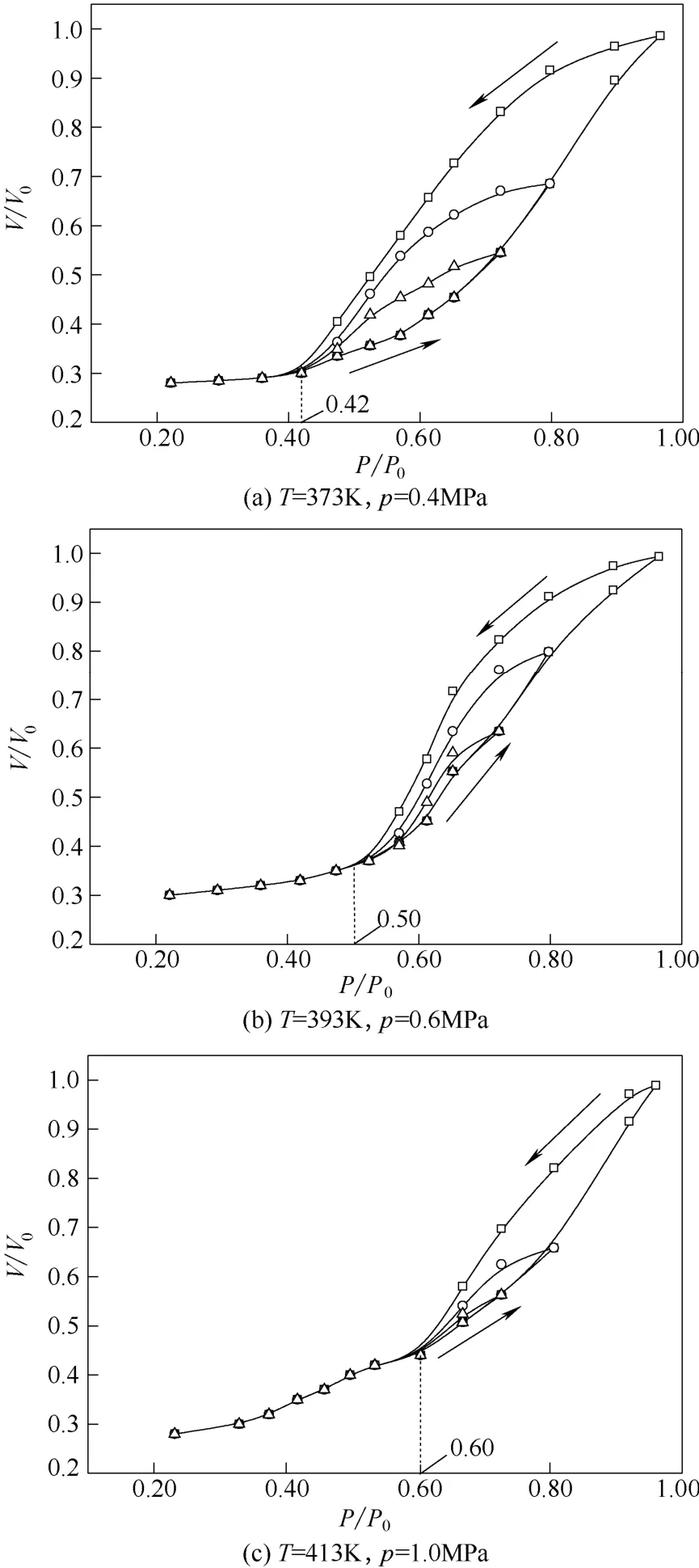
圖3 溫度對環己烷吸附行為的影響Fig.3 Effect of temperature on adsorption isotherms ofcyclohexane

3.2 臨界滯后孔半徑

給定溫度和吸附質（環己烷）條件下，rch與相對壓力之間的關系如圖4所示。環己烷在373、393、413 K 3 個溫度條件下，臨界滯后孔半徑為平均孔半徑5.01 nm 時，對應相對壓力依次是0.71、0.74、0.76。當T=373 K，P/P0=0.71 時，孔半徑小于5.01 nm 的孔都發生毛細凝聚，由圖1孔徑分布圖可知此時有近半數的孔半徑小于5.01 nm。隨著溫度的升高，相同孔徑的毛細孔發生毛細凝聚所需相對壓力增大，即溫度越高，發生毛細凝聚越困難。

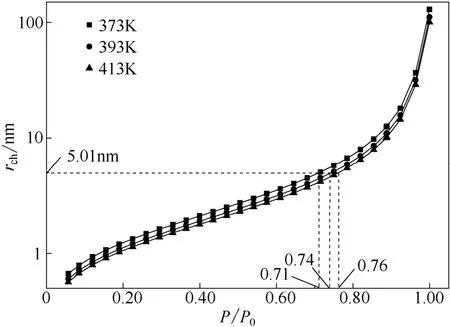
圖4 溫度對臨界滯后孔半徑的影響Fig.4 Effect of temperature on critical hysteresis pore radius of CuO/ZnO/γ-Al2O3

3.3 有效擴散系數隨溫度和壓力的變化

實驗測定了373、393、413 K 3 種溫度條件下環己烷在多孔催化劑內發生毛細凝聚時，氫氣有效擴散系數De與環己烷蒸氣相對壓力P/P0的關系，如圖5所示。

由圖5可以明顯看到在一定溫度下，隨著P/P0增大，De逐漸降低，當P/P0接近0.8 時降幅減緩至穩定，此時有效擴散系數接近氣體在液相中的有效擴散系數，可以認為催化劑孔內由于發生毛細凝聚現象而處于接近“完全潤濕”狀態。脫附時隨著P/P0的減小，氫氣的有效擴散系數起始段增加緩慢，之后顯著上升，并且也會出現類似吸附等溫線中的明顯的滯后環。

對比圖5(a)、(b)、(c) 在P/P0相等時的有效擴散系數可知，隨著溫度升高，有效擴散系數略微下降。原因是3 種操作溫度遞增幅度不大，但壓力增加很明顯，有效擴散系數下降也符合一般規律。在373、393、413 K 滯后環的起點對應的相對壓力依次為0.42、0.50、0.60。從圖4可知隨著溫度的升高，相同孔徑的毛細孔發生毛細凝聚所需相對壓力增大，說明溫度越高，吸附質越難在孔內發生冷凝，此時等溫吸附量與脫附量之間差別也越小，有效擴散系數也越接近，在圖5中就表現為隨著溫度的增加，滯后環向相對壓力P/P0增大的方向移動，并且寬度變窄。

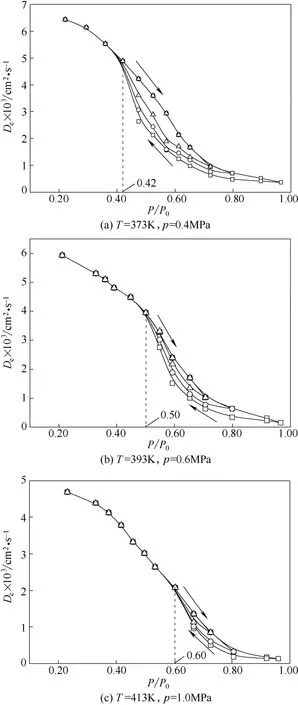
圖5 溫度對氫氣的有效擴散系數的影響Fig.5 Effect of temperature on effective diffusivity of hydrogen

從圖5可以看出，滯后環起點之前的有效擴散系數下降幅度小于滯后環起點之后的下降幅度，表明多分子層吸附比毛細凝聚對有效擴散系數的影 響要弱。有效擴散系數的理論預測值與實驗值吻合較好，說明所選用的數學模型準確且適用該實驗 條件。

3.4 不同溫度下有效擴散系數與內部潤濕分率之間的關系

將吸附實驗得到的吸附等溫線數據代入式(6)求解相同操作條件下內部潤濕分率，可得De與fw之間的關系，如圖6所示。在每種情況下，“全干”狀態（fw接近于0）時氫氣的有效擴散系數De,g和“全濕”狀態（fw接近于1）時氫氣的有效擴散系數De,l存在巨大差距，De,g最大可為 4.90×10-3cm2·s-1，De,l最小為0.21×10-3cm2·s-1，后者是前者的4.28%。由圖6可知在3 種操作條件下，有效擴散系數均隨著內部潤濕分率的增加呈現先急劇下降、后趨于穩定的趨勢。3 種情況fw相等時，有效擴散系數也不同，原因是3 種情況操作溫度雖相差不大，但操作壓力相差較大。在fw≤0.4 范圍內，3種溫度條件下fw相等時氫氣的有效擴散系數有明顯差別；在fw≥0.6 范圍內，由于催化劑內部潤濕較為嚴重，3 種溫度條件下氫氣的有效擴散系數接近，操作條件對其影響不大。可見催化劑內部潤濕分率越小，有效擴散系數對操作條件的變化越敏感。由圖6可以看出，De實驗值和fw為非線性關系，并且當m=0.401、n=4.305 時3 種工況下的De計算值和實驗值均吻合較好，說明該關聯式可較為準確地預測不同內部潤濕分率下的氫氣有效擴散系數。

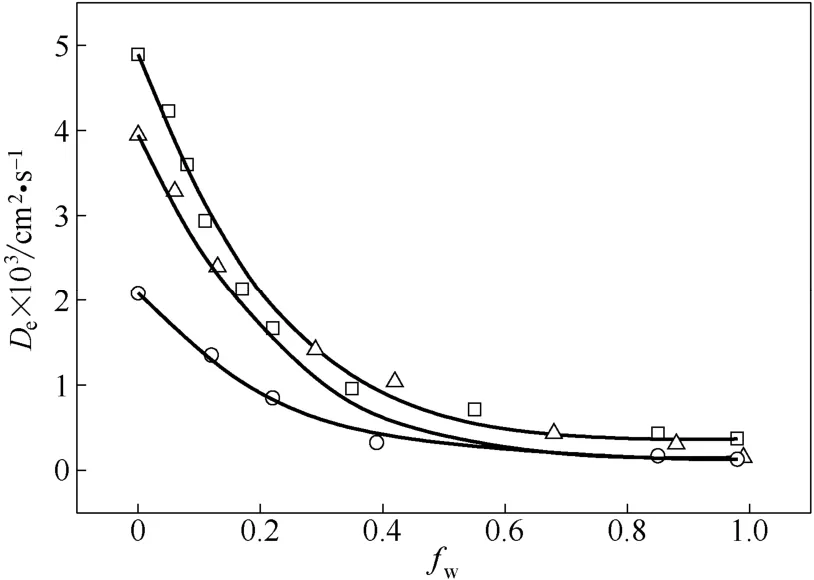
圖6 氫氣的有效擴散系數和催化劑內部潤濕分率的關系Fig.6 Plot of effective diffusivity of hydrogen against catalyst internal wetting fraction

4 結 論

（1）采用改進型單顆粒穩態擴散池測量多孔 催化劑內發生毛細凝聚時氫氣的有效擴散系數，得到的De與P/P0曲線出現明顯的滯后環。隨著溫度的升高，滯后環起點朝著環己烷蒸氣相對壓力增大的方向移動，且寬度變窄。

（2）將雙組分擴散、催化劑孔徑分布、孔結構類型、可凝性物質在催化劑孔道內發生毛細凝聚等因素結合起來，建立了計算多孔催化劑部分潤濕時氫氣有效擴散系數的數學模型。實驗結果驗證了該模型的準確性。

（3）通過重量法測得的吸附等溫線和單顆粒穩態法測量的氫氣有效擴散系數結合得到De與fw關系曲線。催化劑內部潤濕分率越小，氫氣的有效擴散系數對操作條件的變化越敏感。催化劑部分潤濕時氫氣的有效擴散系數與催化劑“全干”、“全濕”時的有效擴散系數及內部潤濕分率之間的關系式為實驗值與計算值吻合較好。

符 號 說 明

De,g——催化劑“全干”狀態時的有效擴散系數，cm2·s-1

De,l——催化劑“全濕”狀態時的有效擴散系數，cm2·s-1

De,t——綜合有效擴散系數，cm2·s-1

f——孔徑分布函數

fw——內部潤濕分率

M——分子摩爾質量，g·mol-1

N——氣體擴散通量，mol·m2·s-1

P——可凝性物質蒸氣的氣相分壓，MPa

P0——可凝性物質在給定溫度下的飽和蒸氣壓，MPa

p——操作壓力，MPa

r——孔半徑，nm

——催化劑平均孔半徑，nm

S——分子的投影面積，nm2

V——可凝性物質在催化劑孔內的吸附量，ml

VS——吸附等溫線滯后環起點對應吸附量，ml

V0——催化劑的孔隙體積，ml

v——單位質量催化劑所具有的孔體積，cm3·g-1

ε——催化劑孔隙率

ρ——吸附質在對應溫度下的密度，g·cm-3

σ——液體在對應溫度時的表面張力，mN·m-1

τ——催化劑曲節因子

下角標

ch——臨界滯后

g——氣相

l——液相

m——分子

w——潤濕狀態

[1]Bhatia S K.Steady state multiplicity and partial internal wetting of catalyst particles [J].AIChE Journal,1988,34 (6):969

[2]Watson P C.Dynamic effects of vaporization with exothermic reaction in a porous catalytic pellet [J].AIChE Journal,1993,39 (6):898

[3]Zheng Q,Yu B M,Wang S F,Luo L.A diffusivity model for gas diffusion through fractal porous media [J].Chemical Engineering Science,2012,68:650-655

[4]Zheng Q,Xu J,Yang B,Yu B M.Research on the effective gas diffusion coefficient in dry porous media embedded with a fractal-like tree network [J].Physical A,2013,392:1557-1566

[5]Mezedur M M,Kaviany M.Effect of pore structure,randomness and size on effective mass diffusivity [J].AIChE Journal,2002,48:15-24

[6]Mu D Q,Liu Z S,Huang C,Djilali N.Determination of the effective diffusion coefficient in porous media including Knudsen effects [J].Microfluid Nanofluid,2008 (4):257-260

[7]Wang Shuxiong (汪叔雄),Zhang Hong (張虹),Lü Dewei (呂德偉).The determination of the effective diffusion coefficient in porous catalyst [J].Chemical Reaction Engineering and Technology(化學反應工程與工藝),1985 (4):25-32

[8]Wang Guirong (王桂榮),Wang Fumin (王富民),Xin Feng (辛峰).Measurement of the tortuosity factor of porous solid catalyst using improved diffusion cell [J].Petrochemical Technology(石油化工),2002 (1):14-17

[9]Nguyen P T M,Do D D,Nicholson D.Pore connectivity and hysteresis in gas adsorption:a simple three-pore model [J].Colloidsand Surfaces A:Physicochem.Eng.Aspects,2013,437:56-68

[10]Alejandro R,Ligia S,Mónica M,Johans R.Simulation of nitrogen adsorption-desorption isotherms.Hysteresis as an effect of pore connectivity [J].Chemical Engineering Science,2005,60:4702-4708

[11]Wang Y,Do D D,Herrera L F,Nicholson D.On the condensation evaporation pressures and isosteric heats for argon adsorption in pores of different cross-sections [J].Colloids and Surfaces A:Physicochem.Eng.Aspects,2013,420:96-102

[12]Zhou Zhiming (周志明),Li Zhuo (李卓),Cheng Zhenmin (程振民).Adsorption on γ-Al2O3of benzene and cyclohexane at high temperature and pressure [J].Process in Natural Science(自然科學進展),2004,14 (2):161-165

[13]Yu Y M,Cheng Z M,Zhou Z M,Wu S C,Liu P,Jin J.Regulation of catalytic reactionviavapor phase condensation (Ⅰ):Experimental study on the reaction rate hysteresis loop [J].Ind.Eng.Chem.Res.,2012,51:8735-8741

[14]Wu S C,Cheng Z M,Liu P,Yu Y M,Jin J,Zhou Z M.Pore network effects under the reduction of catalyst size at elevated temperatures [J].Chemical Engineering Science,2013,93:350-361

[15]Li Zhuo (李卓),Zhou Zhiming (周志明),Cheng Zhenmin (程振民).Study on the reaction characteristics of the internal partial wetted catalyst particles [J].Process in Natural Science(自然科學進展),2004,14 (11):1325-1328

[16]Ravikovitch P I,Neimark A V.Experimental confirmation of different mechanisms of evaporation from ink-bottle type pores:equilibrium,pore blocking and cavitations [J].Langmuir,2002,18 (25):9830-9837

[17]Cheng Z M,Zhou Z M,Yuan W K.Determination of catalyst wetting fraction on the molecular level [J].AIChE Journal,2007,53:741-745

[18]Evans R B,Watson G M,Mason E A.Gas diffusion in porous media at uniform pressure [J].Chem.Phys.,1961,35:2076-2083

[19]Johnson M F L,Stewart W E.Pore structure and gas diffusion in solid catalysts [J].Journal of Catalysis,1965,4:248-252

[20]Hessari F A,Bhatia S K.Reaction rate hysteresis in a single partially internally wetted catalyst pellet:experiment and modeling [J].Chemical Engineering Science,1996,51 (8):1241