混合隔振系統(tǒng)逆解耦多線譜主動(dòng)控制

胡世峰，朱石堅(jiān)，何其偉

（海軍工程大學(xué)　船舶與動(dòng)力學(xué)院，武漢430033）

混合隔振系統(tǒng)逆解耦多線譜主動(dòng)控制

胡世峰，朱石堅(jiān)，何其偉

（海軍工程大學(xué)船舶與動(dòng)力學(xué)院，武漢430033）

由潛艇動(dòng)力機(jī)械周期振動(dòng)引起的輻射噪聲是潛艇隱蔽航行的主要噪聲源，在頻域中表現(xiàn)為中低頻多根分立的線譜，嚴(yán)重影響潛艇的聲隱身技術(shù)性能。針對潛艇動(dòng)力機(jī)械隔振系統(tǒng)存在的多根線譜問題，提出混合隔振系統(tǒng)逆解耦的多線譜控制方法。系統(tǒng)闡述混合隔振系統(tǒng)逆系統(tǒng)的構(gòu)建方法、逆系統(tǒng)解耦的結(jié)構(gòu)以及逆系統(tǒng)解耦后附加控制器的設(shè)計(jì)方法。最后，給出一個(gè)設(shè)計(jì)實(shí)例并進(jìn)行仿真計(jì)算，結(jié)果表明基于逆系統(tǒng)解耦的方法能夠有效的降低系統(tǒng)中存在的多根線譜。

振動(dòng)與波；逆系統(tǒng)解耦；混合隔振；多線譜

潛艇在隱蔽航行狀態(tài)下，由動(dòng)力機(jī)械振動(dòng)引起的輻射噪聲是主要噪聲源，且多表現(xiàn)為中低頻分立的線譜，嚴(yán)重影響潛艇的聲隱身技術(shù)性能［1］。目前，國內(nèi)外線譜主動(dòng)控制研究絕大多數(shù)都是采用自適應(yīng)濾波的前饋控制技術(shù)［3-7］，而且取得了許多成果，但是該算法對參考信號和外加信號比較敏感，對于未知的干擾會(huì)失效，魯棒性差，同時(shí)對系統(tǒng)硬件性能要求較高。

基于逆系統(tǒng)解耦的方法是近幾年在非線性控制研究中發(fā)展起來的，不但能夠使系統(tǒng)輸入和輸出解耦，同時(shí)還能夠使非線性系統(tǒng)線性化，已被用于飛機(jī)姿態(tài)控制［8］、交流傳動(dòng)控制［9］。若將混合隔振系統(tǒng)視作一個(gè)多輸入和多輸出系統(tǒng)，通過逆解耦控制使系統(tǒng)的輸入和輸出之間解耦，然后對于解耦后的子系統(tǒng)分別設(shè)計(jì)控制器，將大大簡化系統(tǒng)設(shè)計(jì)，同時(shí)取得良好的隔振效果和抑制線譜。

逆系統(tǒng)解耦控制的重點(diǎn)有兩個(gè)：

（1）系統(tǒng)逆存在的分析與構(gòu)建；

（2）解耦后各自子系統(tǒng)控制器的設(shè)計(jì)。下面將圍繞以上兩點(diǎn)，詳細(xì)闡述基于逆系統(tǒng)解耦控制方法在混合隔振系統(tǒng)多線譜控制中的應(yīng)用。

1　混合隔振系統(tǒng)逆系統(tǒng)的構(gòu)建

1.1混合隔振的動(dòng)力學(xué)模型

在逆系統(tǒng)解耦控制理論中，依據(jù)系統(tǒng)可解耦性原則，系統(tǒng)的輸入維數(shù)必須等于輸出維數(shù)。將柔性基礎(chǔ)簡化成為具有一個(gè)等效質(zhì)量、一個(gè)等效剛度和一個(gè)等效阻尼的動(dòng)力學(xué)模型［10］，系統(tǒng)如圖1所示。

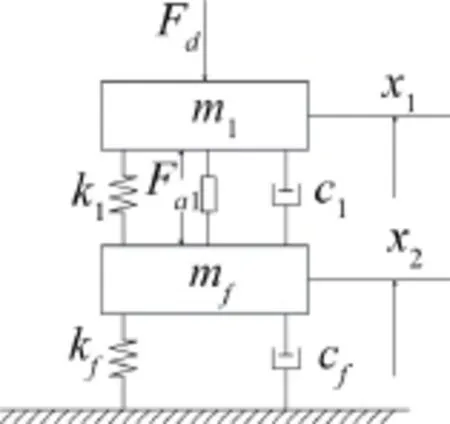
圖1　混合隔振系統(tǒng)動(dòng)力學(xué)模型

圖中Fd表示動(dòng)力機(jī)械的激擾力，F(xiàn)a1表示兩個(gè)可控的作動(dòng)力，m1、mf分別表示動(dòng)力機(jī)械的質(zhì)量和基礎(chǔ)的等效質(zhì)量，x1、x2分別表示m1和mf的振動(dòng)位移，k1、c1表示混合隔振系統(tǒng)的被動(dòng)元件參數(shù)，kf、cf表示基礎(chǔ)的等效剛度和阻尼。

由此整個(gè)混合隔振系統(tǒng)就可看作一個(gè)兩輸入（Fd和作動(dòng)器輸入）兩輸出（m1和mf的振動(dòng)）系統(tǒng)。根據(jù)鍵合圖建模理論［11］，可以迅速的畫出混合隔振的鍵合圖模型如圖2所示，并得到系統(tǒng)的狀態(tài)方程。

圖2　混合隔振系統(tǒng)鍵合圖模型

根據(jù)圖2可知，設(shè)混合隔振系統(tǒng)的狀態(tài)變量為：X1=［p4q7q11p13］T，輸入變量U=［Se1，Se2，Se3］。根據(jù)廣義動(dòng)量和廣義位移的定義，再結(jié)合共勢節(jié)點(diǎn)和共流節(jié)點(diǎn)的特征可以得到如下狀態(tài)方程組

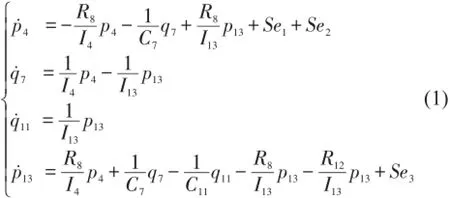
1.2混合隔振系統(tǒng)逆系統(tǒng)的存在性分析

圖1所示的混合隔振系統(tǒng)是一個(gè)典型的兩輸入和兩輸出系統(tǒng)，要將一個(gè)原兩輸入和兩輸出系統(tǒng)解耦成2個(gè)相互獨(dú)立的單輸入單輸出子系統(tǒng)，根據(jù)逆系統(tǒng)解耦控制原理可知混合隔振系統(tǒng)必須可逆，且能夠在物理?xiàng)l件下實(shí)現(xiàn)。

文獻(xiàn)［9］介紹了很重要的系統(tǒng)求逆運(yùn)算算法Interactor算法，下面不加證明的給出利用該算法判斷混合隔振系統(tǒng)可逆性的方法。

設(shè)多輸入多輸出系統(tǒng)（MIMO）的動(dòng)力學(xué)特性由如下方程加以描述式中x為系統(tǒng)的狀態(tài)矢量，u為系統(tǒng)的輸入矢量，y為系統(tǒng)的輸出矢量，f（?）、h （?）為線性函數(shù)。

［定義1］若對MIMO系統(tǒng)輸出函數(shù)采用Interactor算法y=h （x，u）求導(dǎo)，直到矢量中的各個(gè)分量均顯含輸入u，且由于系統(tǒng)的輸出維數(shù)為n，滿足，同時(shí)滿足det那么矢量為系統(tǒng)的矢量相對階，否則MIMO系統(tǒng)不存在矢量相對階。

［定理1］對于式（2）所描述的一般MIMO系統(tǒng)可逆的充分必要條件是系統(tǒng)存在矢量相對階

混合隔振系統(tǒng)的動(dòng)力學(xué)方程如式（1）所示，令x1、x2為系統(tǒng)的狀態(tài)變量，分別代表混合隔振系統(tǒng)中質(zhì)量塊的振動(dòng)位移（見圖1），結(jié)合功率鍵合圖2，并根據(jù)圖中各變量的物理意義可得式（3）。將式（3）代入式（1），可以推得混合隔振系統(tǒng)的振動(dòng)微分方程組如式（4）所示。上述采用功率鍵合圖推導(dǎo)復(fù)雜系統(tǒng)的動(dòng)力學(xué)方程過程非常簡潔，可以避免繁瑣復(fù)雜的受力分析，減少錯(cuò)誤的發(fā)生。

令狀態(tài)變量

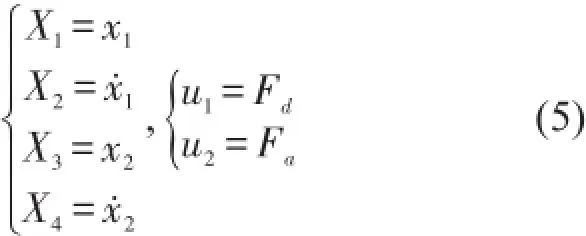
由此可推得，以X=［X1，X2，X3，X4］T為狀態(tài)變量，以U=［u1，u2］T的狀態(tài)微分方程組

其中

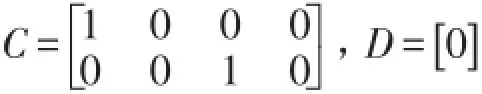
為了采用Interactor算法，簡化推導(dǎo)過程令

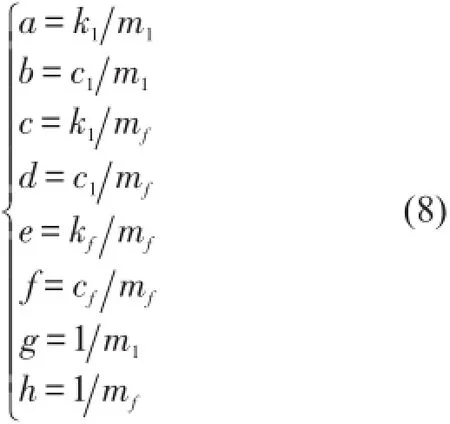
第一步：將X1對時(shí)間求導(dǎo)，直到其t階導(dǎo)數(shù)顯含輸入U(xiǎn) 。

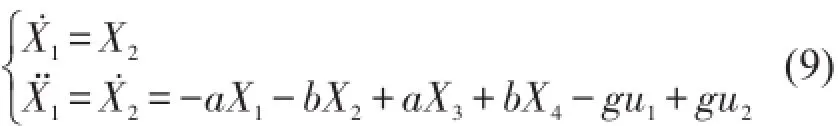
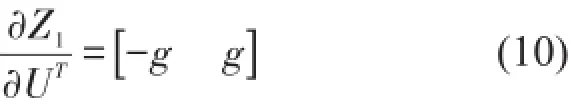
其秩r1=1，矩陣滿秩，所以其相對階為α1=2。

第二步：將X3對時(shí)間求導(dǎo)，直到其t階導(dǎo)數(shù)顯含輸入U(xiǎn)。

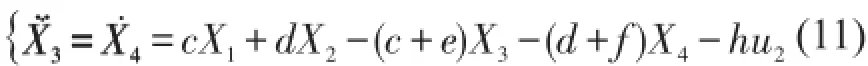
令則由式可知，X3的2階導(dǎo)數(shù)X（2）3顯含輸入U(xiǎn)，于是有

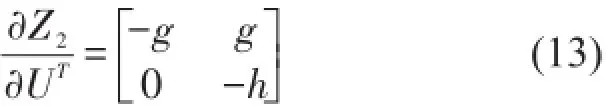
其秩r2=2，矩陣滿秩，所以其相對階為α2=2。

由此可得此混合隔振系統(tǒng)的相對階為α2=［2，2］T，由定理1可知此系統(tǒng)是可逆的，即存在逆系統(tǒng)。

1.3混合隔振逆系統(tǒng)的實(shí)現(xiàn)

將其分別代入式（9）和式（11）可得

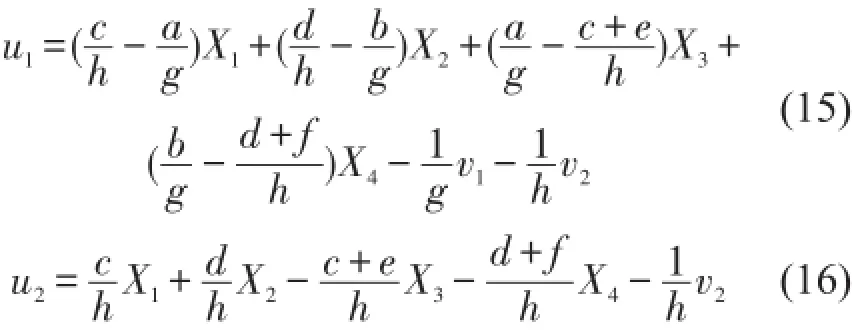
若把v1、v2看作系統(tǒng)輸入而把u1、u2看作系統(tǒng)輸出，系統(tǒng)的狀態(tài)變量仍為，那么式（15）和式（16）可為原混合隔振系統(tǒng)的逆系統(tǒng)的解析實(shí)現(xiàn)。

2　混合隔振逆系統(tǒng)解耦控制

2.1逆系統(tǒng)解耦

由逆系統(tǒng)解耦原理可知一般線性系統(tǒng)可實(shí)現(xiàn)靜態(tài)解耦的充分必要條件是系統(tǒng)存在矢量相對階α。由混合隔振逆系統(tǒng)存在性分析可知的矢量相對階為α=［2，2］T，其矢量本性階為ne=［2，2］T，故可知此混合隔振系統(tǒng)可實(shí)現(xiàn)靜態(tài)解耦。將混合隔振逆系統(tǒng)與原系統(tǒng)復(fù)合組成新的復(fù)合系統(tǒng)。

若令新的變量

則在新的變量下可得新的復(fù)合系統(tǒng)的狀態(tài)方程為

由方程式（18）和方程式（19）可知，復(fù)合系統(tǒng)實(shí)現(xiàn)了輸入和輸出的解耦，其系統(tǒng)結(jié)構(gòu)如圖3所示。

由圖3可知系統(tǒng)解耦后，整個(gè)復(fù)合系統(tǒng)變?yōu)閮蓚€(gè)互不干擾的子系統(tǒng)，可分別施加控制。但是，對于混合隔振來說第一個(gè)系統(tǒng)由于激勵(lì)力是不可控的，所以無法設(shè)計(jì)控制器，但與混合隔振系統(tǒng)隔離振動(dòng)的目的并不矛盾。由文獻(xiàn)［12］可知只要減小下層質(zhì)復(fù)合系統(tǒng)的輸出方程為量塊的振動(dòng)就可隔離艦船動(dòng)力機(jī)械的振動(dòng)傳遞，故只需對第二個(gè)子系統(tǒng)設(shè)計(jì)控制器。

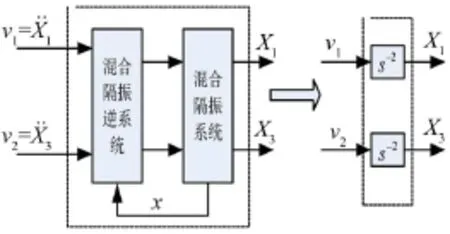
圖3　混合隔振系統(tǒng)狀態(tài)反饋逆系統(tǒng)解耦結(jié)構(gòu)

2.2附加控制器設(shè)計(jì)

解耦后的第二個(gè)子系統(tǒng)的傳遞函數(shù)為

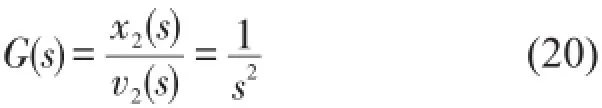
系統(tǒng)的極點(diǎn)處于虛軸上，所以只要系統(tǒng)參數(shù)稍加變化或受到干擾，系統(tǒng)極點(diǎn)極有可能向右偏離，造成系統(tǒng)不穩(wěn)定。因此必須在兩個(gè)子系統(tǒng)前施加反饋控制器使其穩(wěn)定，從而提高逆解耦后系統(tǒng)動(dòng)態(tài)性能和抗干擾能力。控制結(jié)構(gòu)如圖4所示。圖中GC（s）代表所設(shè)計(jì)的反饋控制器，r為參考輸入。

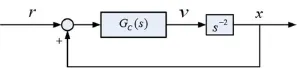
圖4　系統(tǒng)反饋控制結(jié)構(gòu)

PD控制器的傳遞函數(shù)為

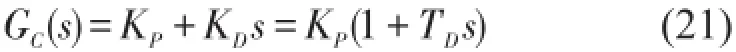
由于開環(huán)傳遞函數(shù)中包含s2項(xiàng)，其相頻特性為-180o，采用PD控制器后，可以將開環(huán)系統(tǒng)的相頻特性抬高到-180o線以上，從而保證系統(tǒng)穩(wěn)定。

通過適當(dāng)選擇參數(shù)KP和TD，以使系統(tǒng)具有一定的相角裕度和帶寬，根據(jù)式（22）可得系統(tǒng)的開環(huán)對數(shù)幅頻特性為

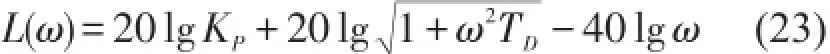
相頻特性為

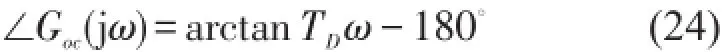
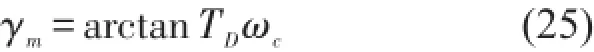
系統(tǒng)的相角裕度為式中ωc為開環(huán)系統(tǒng)的截止頻率。通常ωc的取值應(yīng)與被控對象的物理特性及系統(tǒng)性能要求相符合。

對于采用PD控制器控制2階積分對象，其中低頻段的穩(wěn)態(tài)誤差主要取決于系統(tǒng)開環(huán)增益KP；同時(shí)當(dāng)KP一定時(shí)，TD越大，系統(tǒng)的截止頻率ωc越高，相角裕度越大，系統(tǒng)的超調(diào)越小，調(diào)節(jié)速度越快。針對混合隔振系統(tǒng)，其目標(biāo)是抑制中低頻振動(dòng)（0～200 Hz），系統(tǒng)帶寬可定義為300 Hz，穩(wěn)態(tài)誤差可定義為小于0.1%。由誤差指標(biāo)可確定KPi=2 000，取帶寬指標(biāo)TDi=0.8，于是系統(tǒng)的閉環(huán)環(huán)傳遞函數(shù)為

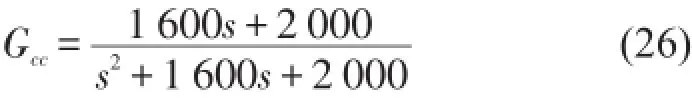
3　實(shí)例仿真與分析

為了驗(yàn)證本文所提出的控制方法有效性，在此引用文獻(xiàn)［13］中提供的實(shí)例數(shù)據(jù)來編寫程序進(jìn)行仿真計(jì)算，并對結(jié)果進(jìn)行分析。

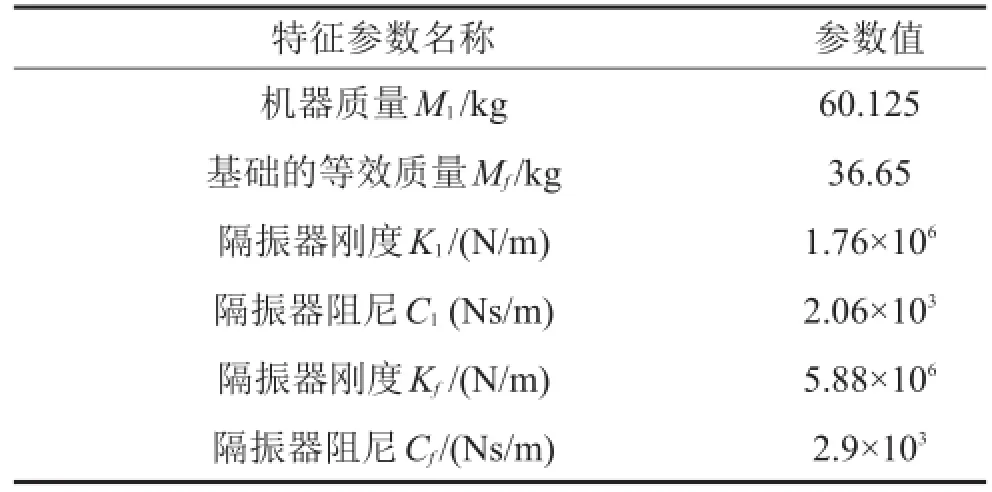
表1　實(shí)例系統(tǒng)的參數(shù)值

具體的仿真計(jì)算方法如下：將表1的參數(shù)值代入式（8），根據(jù)式（9）和式（11）可以建立實(shí)例混合隔振系統(tǒng)的仿真模型，根據(jù)式（14）、（15）和（16）可以建立實(shí)例混合隔振系統(tǒng)的逆系統(tǒng)的仿真模型，采用圖3所示逆系統(tǒng)解耦結(jié)構(gòu)將模型進(jìn)行連接，附加控制器為式（26）。

采用頻率為60 Hz，幅值為60 N的正弦激勵(lì)力輸入系統(tǒng)仿真計(jì)算，仿真結(jié)果如圖5所示。比較仿真結(jié)果圖5中的（a）圖和（b）圖，可知當(dāng)混合隔振系統(tǒng)采用逆系統(tǒng)解耦后，由于外激擾力作用下層質(zhì)量塊產(chǎn)生的位移量級在10-21m，這個(gè)量級的位移可以忽略不計(jì)，即表明外激擾力只對上層質(zhì)量塊產(chǎn)生作用，而對下層質(zhì)量塊不產(chǎn)生作用，從而實(shí)現(xiàn)了解耦。同時(shí)，當(dāng)外激擾力對下層質(zhì)量塊不產(chǎn)生作用，正好達(dá)到了混合隔振的控制目的，消除下層質(zhì)量塊的振動(dòng)。從圖中可以看出逆系統(tǒng)解耦方法可以很好的控制下層質(zhì)量塊的振動(dòng)位移，從而達(dá)到良好的隔振效果。

圖6和7分別為逆解耦方法對多頻正弦激勵(lì)力的仿真結(jié)果，激勵(lì)力頻率分別為60 Hz、100 Hz和150 Hz，幅值分別為60 N、80 N和120 N。圖6（a）和圖7（a）為逆系統(tǒng)解耦控制前后下層質(zhì)量塊的時(shí)間歷程圖，逆系統(tǒng)解耦控制有效的降低整個(gè)下層質(zhì)量塊的振動(dòng)位移，下層質(zhì)量塊的振動(dòng)位移的量級從10-5m下降到10-20m，幾乎可忽略不計(jì)。圖6（b）和圖7（b）為逆系統(tǒng)解耦控制前后下層質(zhì)量塊的頻譜圖，此時(shí)頻譜圖中0 dB位移值為10-12m。從圖中可知不施加逆解耦控制在激勵(lì)頻率處的線譜較為明顯，而施加逆解耦控制后完全消除了激勵(lì)力頻率處的線譜，由此可得逆系統(tǒng)解耦控制方法能夠有效的控制多個(gè)激勵(lì)頻率處的多根線譜。

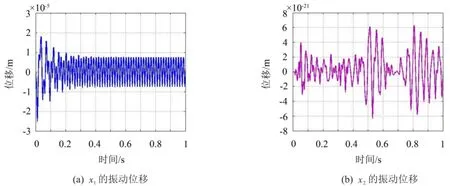
圖5　 60 Hz正弦激勵(lì)下混合隔振系統(tǒng)逆解耦響應(yīng)

4　結(jié)語

中低頻段內(nèi)的多根線譜是潛艇輻射噪聲的顯著特征。混合隔振包含主動(dòng)和被動(dòng)隔振，是控制多根線譜的有效手段。本文詳細(xì)闡述了采用逆系統(tǒng)解耦

圖6　多頻正弦激勵(lì)下混合隔振系統(tǒng)逆解耦前x2響應(yīng)

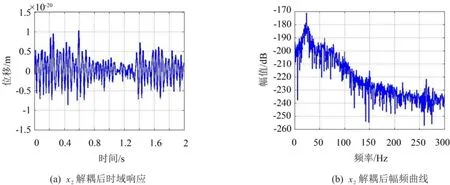
圖7　多頻正弦激勵(lì)下混合隔振系統(tǒng)逆解耦后x2響應(yīng)

控制的方法來控制混合隔振系統(tǒng)中的多根線譜問題，給出混合隔振系統(tǒng)逆系統(tǒng)的構(gòu)建方法、混合隔振逆系統(tǒng)解耦復(fù)合方式以及附加控制器的設(shè)計(jì)方法，最后通過一個(gè)設(shè)計(jì)實(shí)例及仿真計(jì)算，驗(yàn)證了所提出方法的有效性。

通過以上闡述可知逆系統(tǒng)解耦控制的關(guān)鍵是系統(tǒng)逆的構(gòu)建。進(jìn)一步研究方向可為系統(tǒng)魯棒性研究，即系統(tǒng)逆構(gòu)建的不準(zhǔn)確性。自適應(yīng)逆解耦控制研究將采用自適應(yīng)濾波技術(shù)來構(gòu)建系統(tǒng)的逆，可將該方法推廣于柔性基礎(chǔ)。

［1］朱石堅(jiān)，何琳.船舶機(jī)械振動(dòng)控制［M］.北京：國防工業(yè)出版社，2006.

［2］毛偉民.混合隔振技術(shù)研究［D］.武漢：海軍工程大學(xué)，2006.

［3］Zhang Z Y，Chen Y，Yin X W，et al.Active vibration isolationandunderwatersoundradiationcontrol［J］. Journal of Sound and Vibration，2008，318（1-2）:725-736.

［4］Winberg M，Hansen C，Claesson I，et al.Active control of enginevibrationsinacollinsclasssubmarine［R］. Blekinge Institute of Technology Research Report No 2003.11.

［5］卜鋒斌，蔣愛華.自適應(yīng)控制算法在振動(dòng)主動(dòng)控制中的應(yīng)用［J］.噪聲與振動(dòng)控制，2014，34（2）：46-49.

［6］宋港，陳衛(wèi)東.主動(dòng)式自調(diào)諧吸振器在浮筏隔振系統(tǒng)中的應(yīng)用［J］.噪聲與振動(dòng)控制，2012，32（3）：49-54.

［7］張志誼，王俊芳，周建鵬，等.基于跟蹤濾波的自適應(yīng)振動(dòng)控制［J］.振動(dòng)與沖擊，2009，28（2）：64-68.

［8］史靜平.直接力縱向解耦控制方法研究與實(shí)時(shí)仿真系統(tǒng)［D］.西安：西北工業(yè)大學(xué)，2007.

［9］戴先中，劉國海，張興華.交流傳動(dòng)神經(jīng)網(wǎng)絡(luò)逆控制［M］.北京：機(jī)械工業(yè)出版社，2007.

［10］朱石堅(jiān)，樓京俊，何其偉，等.振動(dòng)理論與隔振技術(shù)［M］.北京：國防工業(yè)出版社，2006.

［11］王中雙.鍵合圖理論及其在系統(tǒng)動(dòng)力學(xué)中的應(yīng)用［M］.哈爾濱：哈爾濱工程大學(xué)出版社，2007.

［12］鐘民軍，胡世峰，史鐵林.多步預(yù)測自校正控制算法在混合隔振中的應(yīng)用研究［J］.振動(dòng)與沖擊，2009，28（10）：112-116.

［13］袁紹軍，楊鐵軍，肖友洪，等.雙層隔振系統(tǒng)量化因子模糊自調(diào)整主動(dòng)控制技術(shù)研究［J］.振動(dòng)工程學(xué)報(bào)，2005，18 （2）：208-211.

Multi-line Spectral Control Based on Reciprocal Decoupling in Hybrid Vibration Isolation Systems

HU Shi-feng，ZHU Shi-jian，HE Qi-wei

（College of Ship and Power，Naval University of Engineering，Wuhan 430033，China）

The radiation noise induced by periodic disturbances from the power plant of the submarine is the main noise source for stealing cruise of the submarine.Its performance shows a multi-line spectrum in the low and intermediate frequency bands，which may seriously deteriorate the stealing performance of the submarine.In this paper，a new method for multi-line spectra control based on reciprocal decoupling was proposed.The existence of the reciprocal system of the hybrid vibration isolation system was analyzed.The model of the reciprocal system was built.And the reciprocal decoupling control of the system was designed.Finally，a design and simulation example was presented.According to the results of simulation，it was found that the hybrid vibration isolation system can be controlled by the reciprocal decoupling control algorithm. Moreover，the performance of the hybrid vibration isolation system was much better than the passive system.

vibration and wave；reciprocal decoupling；hybrid vibration isolation system；multi-line spectrum

TB535

ADOI編碼：10.3969/j.issn.1006-1335.2015.05.004

1006-1355（2015）05-0025-05+38

2014－12－04

國防預(yù)研基金項(xiàng)目（1015020102）

胡世峰（1978－），男，講師，研究方向：混合隔振。

E-mail:shifeng_78@126.com

朱石堅(jiān)，男，博士生導(dǎo)師，研究方向：噪聲與振動(dòng)控制、混合隔振、混沌隔振。