一種基于動態過程的燃氣輪機性能降級診斷方法

張 蒙，周登極，張會生，蘇 明

（上海交通大學機械與動力工程學院，上海200240）

由于較高的使用頻率和較重的負荷任務，大型的工業設備都具有一定的使用壽命.在不出現致命性故障的情況下，大多數使用壽命內的設備在正常運行期間的性能會緩慢退化，燃氣輪機也不例外.燃氣輪機在使用壽命內的退化主要來源于氣路部件的性能降級［1］，如壓氣機和渦輪的疲勞、腐蝕、泄漏以及高溫部件的蠕變等.因此，為了保持燃氣輪機良好的工作狀態，當發現運行中的燃氣輪機部件出現較大程度的性能降級時，需要對燃氣輪機的氣路部件進行維護，如壓氣機的水洗操作等.然而，針對燃氣輪機的性能降級，現階段采用的維護方式仍然以定期維護為主，這樣的策略雖然便于操作，但是存在維護不及時和過度維護的雙重風險，所以以狀態監測為基礎的視情維護和故障診斷就顯得十分必要.

狀態監測所能獲取的信息是燃氣輪機的運行參數，以此為樣本進行分析可以得知機組性能的降級程度.這些樣本中的參數主要為壓力和溫度等信號，這些信號的故障診斷與分離所采用的方法［2-3］主要只對穩態時的數據進行分析，因此存在以下問題：（1）穩態參數往往難以得到，工況變化過程中無法判斷性能降級程度；（2）有時部件性能降級導致的運行參數的穩態測量值變化較小，有被誤認為是誤差的風險［4］.

鑒于以上缺陷，筆者提出了一種基于動態過程的燃氣輪機性能降級診斷方法，與利用穩態偏差進行判斷分析的方法相比，該方法對燃氣輪機性能降級的反映更加有效.

1 動態過程的診斷方法

要研究燃氣輪機部件性能降級與運行參數間的變化關系，需要對機組性能降級前后的運行參數進行比較.針對基于動態過程的診斷方法，進行比較的運行參數是一條時域的趨勢曲線.

1.1 基于模型的比較方法

在燃氣輪機實際診斷過程中，使用的是來自正常運行機組的運行參數.在方法研究時，事先并不知道部件是否發生了性能降級或者降級程度如何，因此采用模型進行分析，可以明確規定發生的降級情況，通過正常狀態的模型（以下簡稱正常模型）與降級處理后的模型（以下簡稱降級模型）的運行參數曲線比較，可以有效地討論性能降級與運行參數變化間的關系.采用指定燃氣輪機某一部件進行某一種性能降級的方式，觀察運行參數隨之變化的動態過程.

建立好動態模型后，以此作為正常運行機組，對指定的動態過程進行計算，可以得到正常工作時運行參數的響應曲線；對特性線進行降級處理，通常對特性線乘以指定的降級系數進行放縮后，再進行給定動態過程的計算.基于上述方法，可以得到正常模型的運行參數與指定部件性能降級后的運行參數，從而進行有針對性的分析，具體流程見圖1.

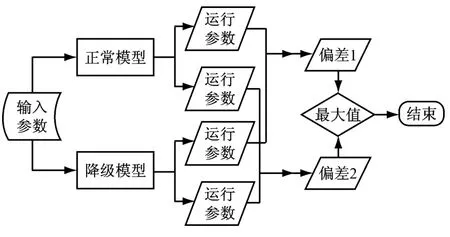
圖1 研究方法流程圖Fig.1 Flowchart of the research method

由于運行參數的種類很多，包括流量、溫度和壓力等，從在降級前后通過比較不同運行參數獲得不同的偏差值中，選出最顯著有效的值以確定與對應降級有最大相關性的運行參數進行分析［5］.

1.2 累積偏差

在燃氣輪機動態過程中，狀態監測輸出的是運行參數隨時間變化的動態響應曲線.

在穩態系統的比較中，運行參數的穩態偏差Δz通常為

式中：z為系統可觀測的運行參數，對于燃氣輪機而言，包括溫度、壓力和流量等；zn為正常狀態下的穩態值，此時理論上沒有任何降級發生，而z代表當前評估時的穩態值，兩者的偏差為Δz.

對于與時間相關的動態過程，每一個時刻的運行點并不是關心的重點，因此上述的穩態偏差無法對整個動態過程進行有效的描述.與此相對應的一種累積偏差［6］常用來衡量當前動態變量與原始動態變量間的偏差，如圖2所示.

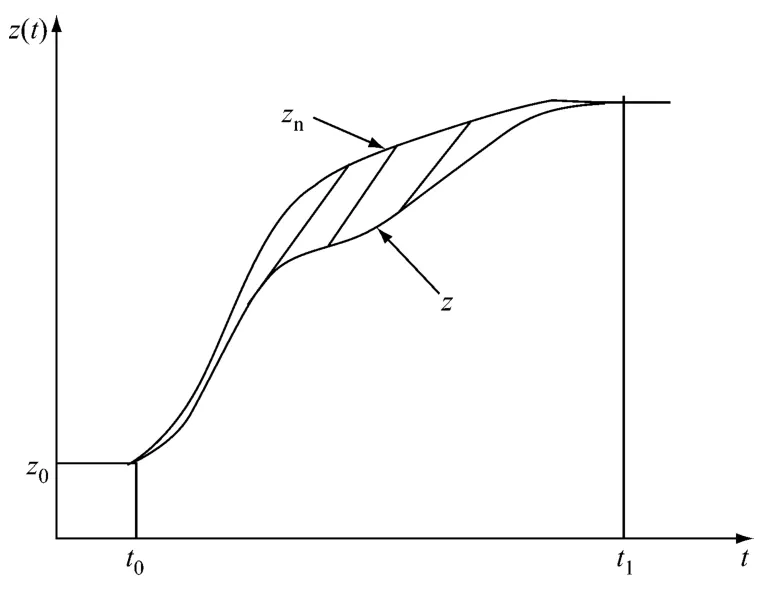
圖2 累積偏差處理示意圖Fig.2 Processing with accumulative deviation

定義累積偏差為Δz′，則有

為了防止動態系統初值對偏差敏感度的干擾，將累積偏差處理為

在數值積分時，采樣時間取0.1s，可將式（3）寫成離散形式：

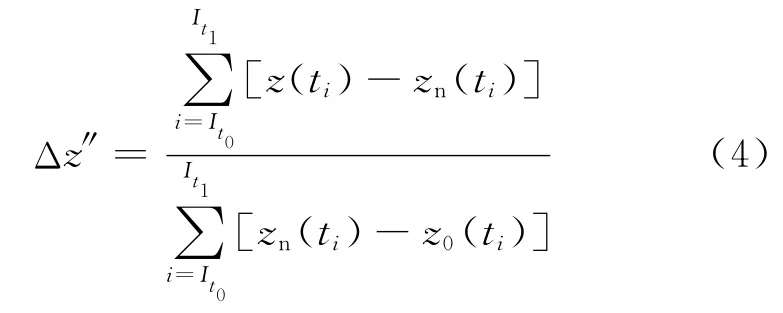
式中：［Ⅰt0，Ⅰt1］表示離散區間.

在采樣時間足夠短的情況下，累積偏差不受噪聲的干擾.

當z為燃氣輪機的某一運行參數時，采用上述計算方法得出的累積偏差Δz″就可以作為該運行參數的整體偏差，可用于反映和判斷燃氣輪機的性能降級情況.

1.3 燃氣輪機動態模型

在上述研究方法中，需要建立一個可靠的燃氣輪機動態模型來實現運行參數的獲取與性能降級過程的處理.

1.3.1 燃氣輪機模型的基本結構

燃氣輪機主要由壓氣機、燃燒室、渦輪和轉子構成.采用模塊化建模方式搭建動態模型，該模型也主要區分為這4個模塊［7］.

采用面向對象的模塊化建模思路可以化繁為簡，將復雜的系統簡化為簡單的子系統，只需對各子模塊進行單獨建模調試，最后整合在一個總的模型中即可［8］.對燃氣輪機進行建模時，主要在燃燒室模塊和轉子模塊中考慮系統的容積慣性和轉子的轉動慣性，因此壓氣機與渦輪可以假定為準穩態模塊.

以某單軸燃氣輪機為例，依次從各部件的模型建立到整體模型的搭建來介紹該燃氣輪機動態模型的建立過程.該燃氣輪機設計點的額定功率為240 MW，燃料為天然氣，壓比為15.5，壓氣機空氣質量流量為613kg／s，渦輪排溫為594 ℃，燃料量為13.58kg／s，不考慮抽氣與進口可調導葉（IGV）開度.模型以負荷指令為控制量.

1.3.2 壓氣機模塊與渦輪模塊

整機的建模從壓氣機模塊開始，壓氣機中進行的是空氣的絕熱壓縮過程，采用的是變比熱容的計算方法.壓氣機的輸入量主要有進氣溫度T0、大氣壓力p0、轉速n和壓氣機出口壓力p2，輸出量主要包括出口的流量、焓、溫度、效率、壓比和耗功等.壓氣機的特性圖由骨干線法得到，與設計點進行放縮匹配后得到的特性圖在設計點附近具有較高的準確度.壓氣機的計算過程從確定壓比開始，計算出折合轉速進行查表，得到流量和效率后再進行變比熱容的熱力計算［9］.

渦輪的模型與壓氣機類似，輸入量包括前一階段輸出的各種狀態參數和轉速，輸出量為出口的流量、焓、溫度、效率、壓比和輸出功等.

1.3.3 燃燒室模塊

燃燒室模塊主要考慮系統的容積慣性，考慮到燃燒室的容積慣性，進出口流量的不平衡造成了容積中流體壓力的變化，壓氣機與渦輪間的流量平衡問題被轉化為燃燒室的壓力變化，按照上述考慮，能量平衡與流量平衡可以用以下2 個微分方程來表示，據此求取出口焓和壓力.

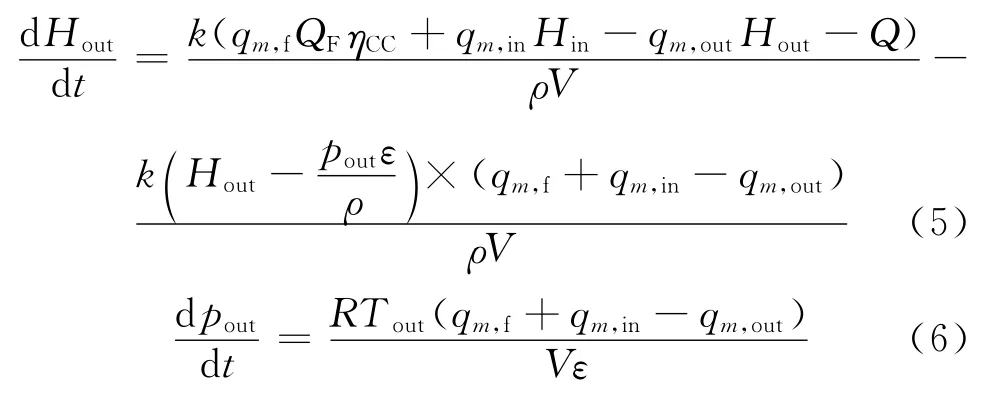
式中：ηCC為燃燒效率；ε為壓損系數；Q為向外放熱量，kW；k為絕熱指數；ρ為密度，kg／m3；p為壓力，Pa；H為焓，kJ／kg；QF為燃氣的低位熱值，kJ／kg；R為通用氣體常數；qm為質量流量，kg／s；V為壓氣機、渦輪進排氣管路與燃燒室體積總和，m3；T為溫度，K；下標f、in和out分別表示燃氣、進口和出口.

燃燒室模塊的進口參數與實際燃氣輪機相同，油量通過轉速和PI控制器直接控制.

1.3.4 轉子模塊

轉子是連接壓氣機與渦輪的部件，渦輪的輸出功主要通過轉子來傳遞給壓氣機和負載.當渦輪的輸出功與壓氣機的耗功和負載功率相等時，轉子處于平衡狀態，系統也會達到某個穩定工況；當上述功率不相等時，轉子的不平衡會使系統處于動態過程，基于這種功率平衡過程的轉子方程如下：

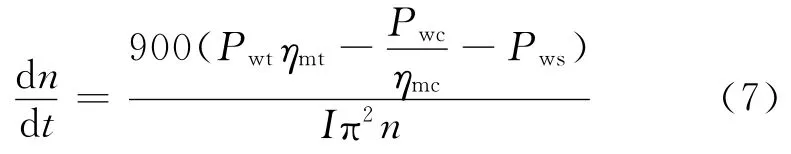
式中：Pwt、Pwc和Pws分別為渦輪輸出功、壓氣機耗功和負載功率，kW；ηmt和ηmc分別為壓氣機和渦輪的機械效率；Ⅰ為轉動慣量.

在構建完各部件后，對模型進行整合，可以得到所需的燃氣輪機動態模型.該模型的結構和氣路走向見圖3.

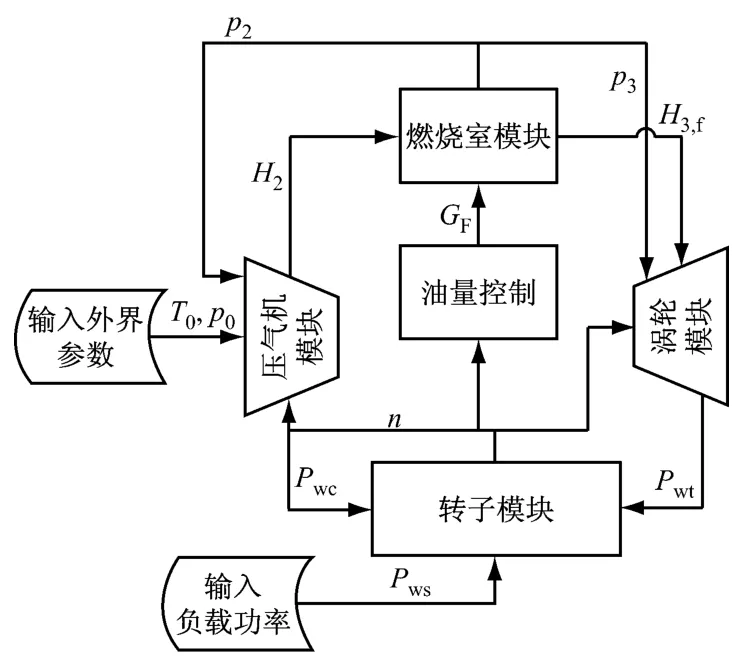
圖3 燃氣輪機模塊化建模結構Fig.3 Modular modeling of the gas turbine

圖3中外界整體模型的輸入參數主要包括大氣壓力、進氣溫度和負載功率.在動態過程中，負載功率隨時間發生變化.

2 基于動態過程診斷方法的應用

燃氣輪機性能降級是由于各個部件性能降級造成的，所涉及到的性能降級有多種可能，筆者主要關注通流部件即壓氣機和渦輪的性能降級.動態過程確定為負載功率從200 MW 階躍變化到240 MW，根據仿真結果，其過渡過程時間約為150s.根據上文所提到的方法，可以求出各運行參數在過渡過程中的累積偏差和最終的穩態偏差.

通流部件的性能降級主要體現在效率降低和通流率降低2個方面，體現在特性圖上就是效率和折合流量對應的特性線平移.因此可對2種特性線設定對應的2種降級參數，即特性圖2種參數的降級情況.現將這2種降級參數設定為0.02，即將特性圖的折合流量和效率乘以0.98，完成對應的降級處理，并依次計算出4種性能降級情況下運行參數的累積偏差和最終的穩態偏差，主要包括燃料量GF、壓氣機出口壓力p2、壓氣機出口溫度T2、渦輪前溫度T3和渦輪排溫T4.

應用式（1）計算對應動態過程的穩態偏差，Δz采用動態過程的增量來替代放大穩態增量，式（1）可變為

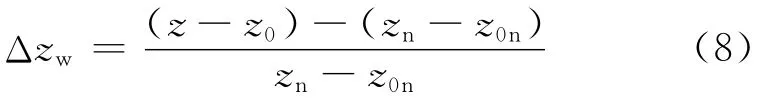
式中：z和zn分別為性能降級后和正常狀態下的終態運行參數；z0和z0n分別為降級后和正常狀態下的初態運行參數.

經過計算得到各運行參數的累積偏差和穩態偏差，結果見表1 和表2，其中降級參數均為無因次量.

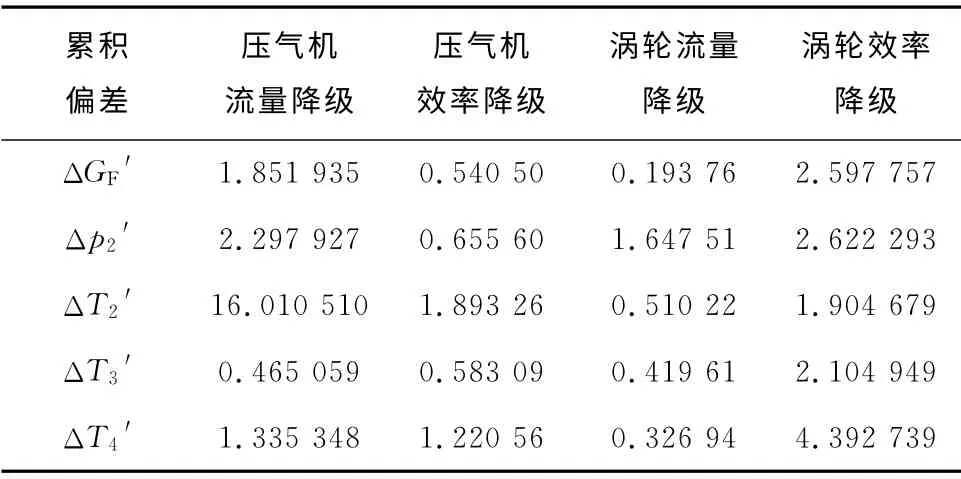
表1 各運行參數的累積偏差Tab.1 Accumulative deviation of each parameter

由表1和表2可以看出，盡管經過從式（1）到式（8）的放大處理，在性能降級發生時各運行參數的穩態偏差仍然是很小的.而對于累積偏差，不同性能降級情況下對應運行參數的反應靈敏度有很大差異.

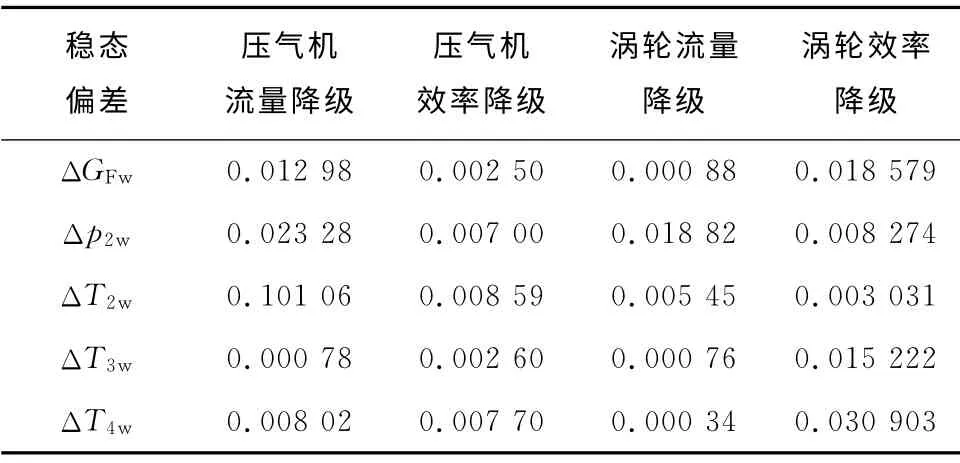
表2 各運行參數的穩態偏差Tab.2 Steady-state deviation of each parameter

下面就從不同的性能降級情況來分析運行參數的累積偏差對性能降級的反映情況.

（1）壓氣機的流量降級.

在壓氣機的流量降級情況下，累積偏差最大的運行參數是T2.正常狀態運行與性能降級后運行時，壓氣機出口溫度T2相對初始狀態的變化曲線如圖4所示，其中T2n和T2cg分別為正常狀態運行和性能降級后運行時T2的響應.由圖4可以看出，動態過程中兩者差異較顯著，穩態過程差異也很大，因此造成了T2累積偏差比其他運行參數累積偏差要大得多的現象.此外，前半段的動態過程較好地反映了來自壓氣機流量的影響，其他3 個降級情況下，T2的前半段都沒有如此顯著的差異.

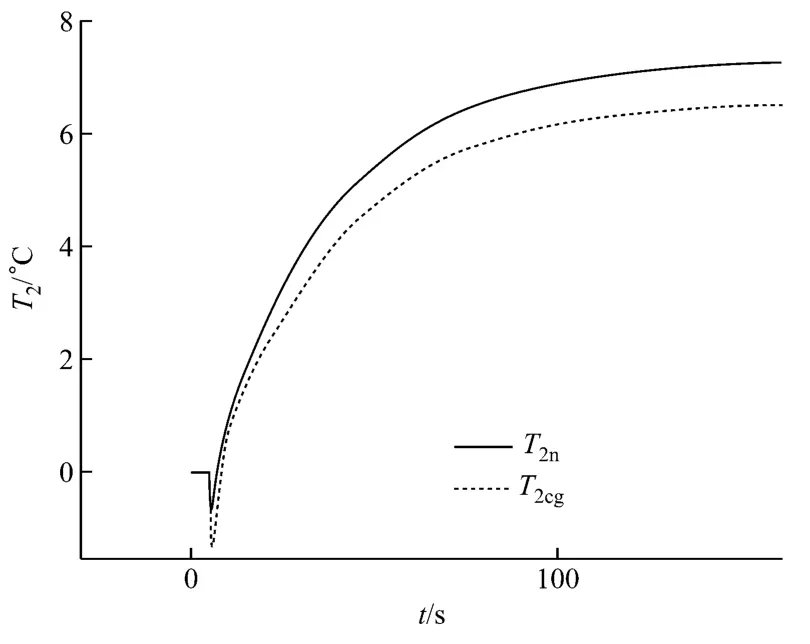
圖4 壓氣機流量降級對T2 的影響Fig.4 Influence on T2caused by compressor flow rate degradation

（2）壓氣機的效率降級.

在壓氣機的效率降級情況下，累積偏差最大的運行參數還是T2，但是p2和T2在這種降級情況下動態區分不顯著，選擇渦輪排溫T4作為分析對象，正常狀態運行與性能降級后運行時，T4相對初始狀態的變化曲線如圖5 所示，其中T4n和T4cef分別為正常狀態運行和性能降級后運行時T4的響應.由圖5可以看出，動態過程中兩者差異明顯，而穩態過程差異不大，動態過程較穩態過程更好地反映了降級情況.

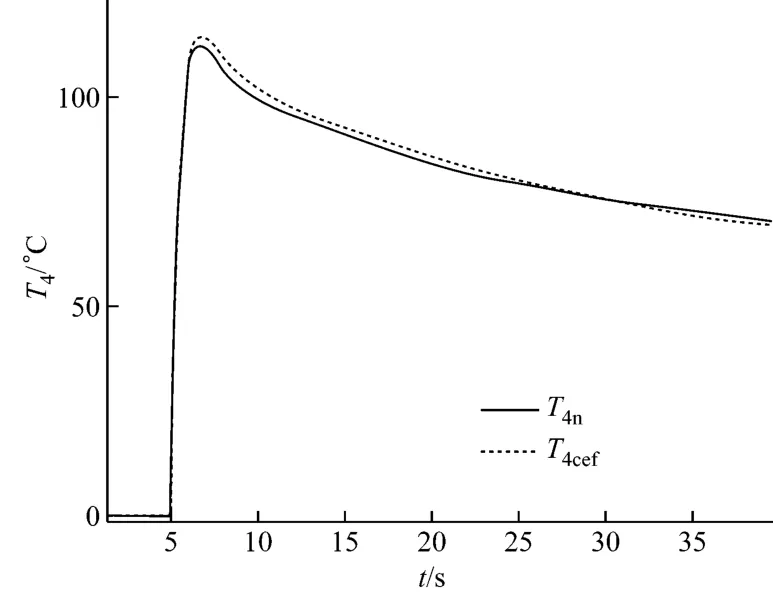
圖5 壓氣機效率降級對T4 的影響Fig.5 Influence on T4caused by compressor efficiency degradation

（3）渦輪的流量降級.

在渦輪的流量降級情況下，累積偏差最大的運行參數是p2，然而p2與T2在這種降級情況下動態區分不顯著，仍選用T4作為分析對象.正常狀態運行與性能降級后運行時，T4相對初始狀態的變化曲線如圖6所示，其中T4n和T4tg分別為正常狀態運行和性能降級后運行時T4的響應.由圖6可以看出，在相同程度的降級情況下，渦輪流量的降級對各運行參數的影響都很小，在小降級時它的觀測值也不準確.

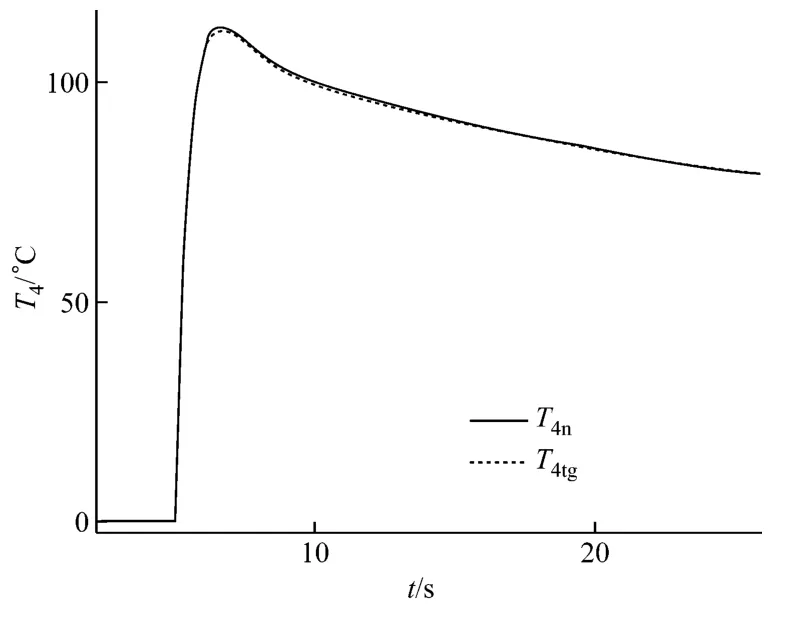
圖6 渦輪流量降級對T4 的影響Fig.6 Influence on T4caused by turbine flow rate degradation

（4）渦輪的效率降級.

在渦輪的效率降級情況下，累積偏差最大的運行參數是T4.正常狀態運行與性能降級后運行時，T4相對初始狀態的變化曲線如圖7所示，其中T4n和T4tef分別為正常狀態運行和性能降級后運行時T4的響應.由圖7可以看出，渦輪的效率降級對各運行參數的影響很大，動態過程中T4的變化比穩態過程更為明顯.

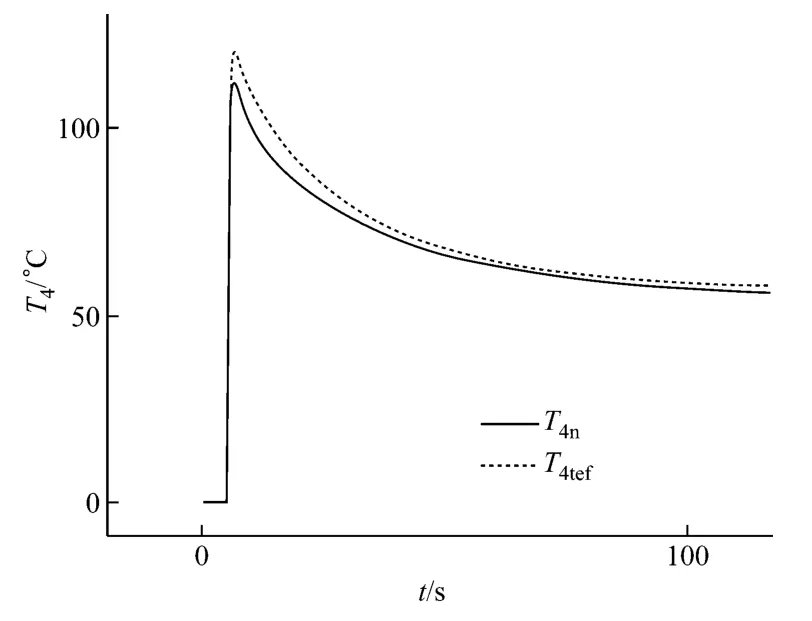
圖7 渦輪效率降級對T4 的影響Fig.7 Influence on T4caused by turbine efficiency degradation

比較以上4 種性能降級情況，可以看出T4作為運行過程變化明顯的運行參數，可以用來表征性能降級情況的發生，而渦輪的流量降級對運行參數的影響很小，只有運行參數的累積偏差值可以反映其降級發生的嚴重程度.另外，單一部件性能降級有可能造成多個運行參數的累積偏差較大，相應地同一個運行參數的累積偏差也可能由多個部件性能降級產生.對于所得到的累積偏差，可以借用航空發動機維護中的概念使用指印圖比照的方式進行故障分析，通過可測參數偏差發生的嚴重程度與偏差方向對性能降級進行初步定位，也可以直接將累積偏差作為非線性故障診斷模型中的目標函數，通過算法優化初值，使得相對實際燃氣輪機的累積偏差最小來迭代出實際燃氣輪機的降級參數.

3 結 論

（1）提出了一種基于動態過程的性能降級診斷方法，整理出通過降級處理燃氣輪機模型對運行參數的累積偏差進行分析的思路.該方法在實際應用時動態運行參數曲線的對比中體現出了其可行性.

（2）在同樣的動態過程中，部分運行參數相比其他運行參數的累積偏差更為明顯，如渦輪排溫T4，可作為部件性能降級的一般特征量.不同的性能降級對不同的運行參數造成的影響有很大不同，使得部分運行參數可以用來表征特定的性能降級.

（3）在不同的性能降級情況下，運行參數的累積偏差變化規律與穩態偏差的變化規律并不一致，在對運行參數影響不明顯的降級過程（如渦輪的流量降級）中，累積偏差與其他相同程度的降級所得到的累積偏差相近，相比穩態參數更好地反映了實際的降級情況.

［1］RAY A.Symbolic dynamic analysis of complex systems for anomaly detection［J］.Signal Processing，2004，84（7）：1115-1130.

［2］DOEL D L.Interpretation of weighted-least-squares gas path analysis results［J］.ASME Journal of Engineering for Gas Turbines and Power，2003，125（3）：624-633.

［3］邢媛.基于離散工作點集擴維的燃氣輪機故障診斷方法研究［D］.哈爾濱：哈爾濱工業大學，2013.

［4］MERRINGTON G L.Fault diagnosis of gas turbine engines from transient data［J］.Journal of Engineering for Gas Turbines and Power，1989，111（2）：237-243.

［5］蒲星星.基于模型的重型燃氣輪機氣路故障診斷研究［D］.北京：清華大學，2013.

［6］LI Yiguang.A gas turbine diagnostic approach with transient measurements［J］.Proceedings of the Institution of Mechanical Engineers，Part A：Journal of Power and Energy，2003，217（2）：169-177.

［7］劉尚明，李忠義.基于SIMULINK 單軸重型燃氣輪機建模與仿真研究［J］.燃氣輪機技術，2009，22（3）：33-39.

LIU Shangming，LI Zhongyi.Modeling and simulation of single shaft heavy-duty gas turbine using SIMULINK［J］.Gas Turbine Technology，2009，22（3）：33-39.

［8］付云鵬，黃宜坤，張會生，等.一種考慮變幾何特性的重型燃氣輪機建模方法［J］.動力工程學報，2014，34（3）：56-60.

FU Yunpeng，HUANG Yikun，ZHANG Huisheng，et al.A modeling method for heavy gas turbines considering variable-geometry characteristics［J］.Journal of Chinese Society of Power Engineering，2014，34（3）：56-60.

［9］鐘芳源.燃氣輪機設計基礎［M］.北京：機械工業出版社，1987：19-32.