一種電荷再分布的逐次逼近AD轉換器設計

高加亭，趙宏建

（中國電子科技集團公司第四十七研究所，沈陽110032）

一種電荷再分布的逐次逼近AD轉換器設計

高加亭，趙宏建

（中國電子科技集團公司第四十七研究所，沈陽110032）

設計了一種電荷再分布逐次逼近AD轉換器電路。通過引入耦合電容CS，整個電容陣列只需要128個單位電容C，相比直接使用二進制加權電容陣列，節省了近97%的單位電容數量。選用Charted 0.35μm Mix Signal，3.3V工藝模型進行設計，仿真結果表明，轉換器的分辨率LSB＝0.6mV，能夠達到12位轉換精度。

逐次逼近；模數轉換器；數模轉換器；電荷再分布

1 引 言

模數轉換器（Analog－to－Digital Converter，ADC）將模擬信號轉換成數字信號，是模擬系統與數字系統接口的關鍵部件，長期以來一直被廣泛應用于雷達、通信、測控、醫療、儀表、圖像和音頻等領域。與其他幾種ADC相比，逐次逼近ADC具有中等轉換精度（一般8～16位）和中等轉換速度（一般5MS/s以下），采用CMOS工藝制造時可以保證較低的功耗和較小的芯片面積，而且易于實現多路轉換，因此在精度、速度、功耗和成本方面具有綜合優勢，市場應用廣泛［1］。

2 電荷再分布逐次逼近ADC設計與分析

使用最普遍的逐次逼近ADC之中，DAC部分采用基于電荷再分布原理電容陣列結構［2］。如果僅僅使用并行二進制加權電容陣列，那么12位DAC需要4096個單位電容，這會大大增加芯片面積，提高成本［3］。所以一般高位數的ADC采用分段式結構，傳統的分段式將其補償電容放在低權位電容陣列，耦合電容CS的取值應使低權位電容陣列的電容之和與其串聯之后的等效電容為一個單位電容，采樣階段是對所有的權電容都進行電荷采樣，如圖1所示。

但是CS這樣一個小數值的電容在版圖設計時會遇到布局問題：如果用單位電容通過串并聯的形式組成耦合電容，由于用到的單位電容個數較多，電容的下極板寄生效應會嚴重影響SAR ADC的線性度；如果用一個比單位電容大一些的電容作為這個耦合電容，則在電容陣列中會出現不匹配現象［4］。

為了克服上述各種電容陣列的困難，改進的分段電容結構陣列可以同時避免分數電容值和懸浮節點的產生。改進型的分段電容陣列SAR ADC如圖2所示。與傳統的分段電容陣列不同的是，將其補償電容在高權位電容陣列，此時耦合電容Cs的大小等于單位電容C0，C1－C6與C7－C12分別是兩個二進制加權的電容陣列，下面來具體分析工作原理及過程。

圖1 傳統的逐次逼近ADC電路原理圖Fig.1 Traditional schematic of SAR ADC

圖2 逐次逼近ADC電路原理圖Fig.2 Schematic of SAR ADC

（1）采樣階段

只對高位段MSB段進行采樣，將開關SIN與VIN閉合，開關SC、S12－S7使電容C0、C12－C7下極板與VIN相接，而開關S0閉合，使它們的上極板與固定電壓VCM相接，開關S6－S1使電容C6－C1下極板與地相接，電荷存儲在高位電容C12－C7，CC以及低位電容和CS的串聯等效電容上，電荷數量為：

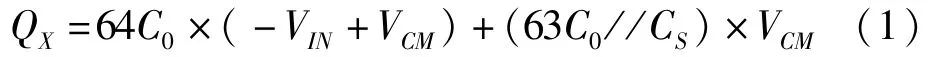
（2）保持階段

S0斷開，SIN與VREF閉合，開關SC、S12－S7以及S6－S1都與地閉合，DAC輸出電壓為：

（3）電荷再分配階段

先將第12位（即MSB）置1，即通過S12將C12的下極板連接到VREF，通過等效電路如圖3（a）所示，因為X點總電荷數不變，可以得到：

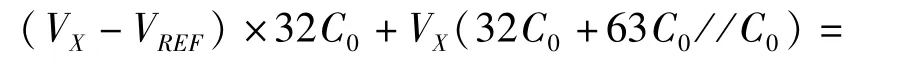
所以DAC輸出電壓為：

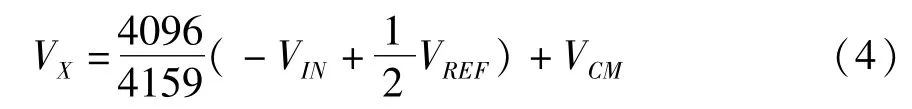
如果VIN＞1/2VREF，那么比較器輸出0，保留第12位為1，否則第12位清0。

依次類推，直到確定了第1位（即LSB），等效電路如圖3（b）所示，由于A點的電荷代數和為0，所以有：

X點的電荷數有：

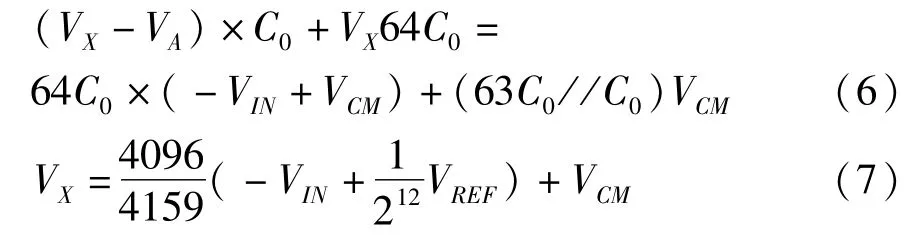
最終，該分段電容結構DAC的輸出為：

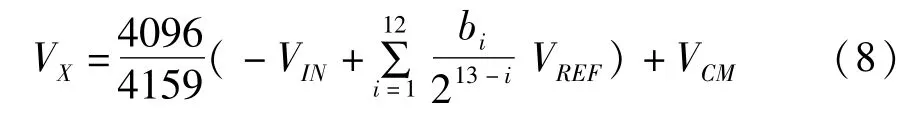
其中，bi是該分段電容結構DAC的第i位值，為0或1。

可見，表達式中僅僅多了一個略小于1的系數，只要設計比較器的分辨率大小足夠分辨出帶有系數的最小精度，對于A/D轉換器的功能以及性能并沒有影響，不影響其線性度。該改進的全二進制加權分段電容陣列結構不僅僅減少了整個芯片的面積，而且所有電容都為單位電容的整數倍，方便了版圖設計和電容匹配。

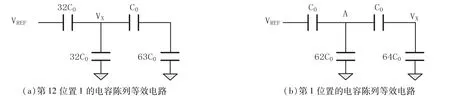
圖3 電荷再分配等效電路Fig.3 Equivalent circuit of charge redistribution

3 電路仿真結果

使用Charted 0.35μm Mix Signal，3.3V工藝模型進行電路設計，在電源VCC＝3.3V，VREF＝2.5V的情況下，對逐次逼近ADC中電容陣列進行掃描，可以得到其輸出特性曲線如圖4所示。

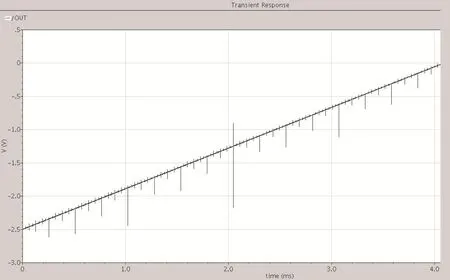
圖4 電容陣列輸出特性曲線Fig.4 Output characteristics of CDAC

放大其中一段得到圖5，LSB＝0.6mV，與理論計算的VREF/4096基本相等。

圖5 輸出特性曲線局部Fig.5 Part of CDAC output characteristics

通過仿真對ADC的理論計算進行驗證，仿真波形如圖6所示，從仿真波形來看，ADC能夠達到12位轉換精度，轉換結果與理論計算相同。

圖6 逐次逼近ADC仿真結果Fig.6 Simulation result of SAR ADC

4 結束語

設計的電荷再分布逐次逼近ADC，通過引入耦合電容，整個電容陣列只需要128個單位電容C，相比直接使用二進制加權電容陣列，節省了近97%的單位電容數量。分析了外加耦合電容CS的計算方法和采樣保持轉換的原理，通過仿真分析，轉換的分辨率LSB＝0.6mV，能夠達到12位轉換精度。

［1］ 孫彤.低功耗逐次逼近模數轉換器的研究與設計［D］.北京：清華大學，2007.

SunTong.Study and Design of Low－power Successive Approximation Analog－to－digital Converter［D］.Beijing：Tsinghua University，2007.

［2］ Takeshi Yoshida，Miho Akagi，Mamoru Sasakiand Atsushi Iwata.A 1V Supply Successive Approximation ADC with rail－to－rail input voltage range［C］.IEEE，2005：192－195.

［3］ Eugenio Culurciello and Andreas Andreou.An 8－bit，1mW Successive Approximation ADC in SOICMOS［C］.IEEE，2003：301－304

［4］ R.Jacob Baker.CMOS電路設計·布局與仿真［M］.劉艷艷，張為，譯.北京：人民郵電出版社，2008.

R.Jacob Baker.CMOSCircuit Design，Layout，and Simulation Second Edition［M］.Beijing：ThePeople’s Posts and Telecommunications Press，2008.

Design of Charge Redistribution SAR DAC

Gao Jiating，Zhao Hongjian
（The 47th Research Institute of China Electronics Technology Group Corporation，Shenyang 110032，China）

The charge redistribution successive approximation analog－to－digital converter is designed in this paper.By adding coupling capacitance CS，128 unit capacitances C are used in the capacitor array，and almost 97%unit capacitances is saved comparing with the directly using binary weighted capacitor array.The simulation is completed by 0.35μm Mix Signal，3.3V processmodel in Charted and the results show that the resolution of the converter（LSB）is 0.6mV and can reach 12 bits conversion accuracy.

Successive approximation；ADC；DAC；Charge redistribution

10.3969/j.issn.1002－2279.2015.06.002

TN752.2

A

1002－2279（2015）06－0006－03

高加亭（1982－），男，吉林省農安市，本科，工程師，主研方向：集成電路工程。

2014－12－17