二自由度門式起重機智能定位防擺控制研究

鄭飛杰，晉芳偉，吳　龍，鄭亞青，邱麗梅，王春榮

（1.三明學院 機電工程學院，福建 三明 365004；2.機械現代設計制造技術福建省高校工程研究中心，福建 三明 365000；3.華僑大學　機電及自動化學院，福建 廈門 361021）

二自由度門式起重機智能定位防擺控制研究

鄭飛杰1,2，晉芳偉1,2，吳龍1,2，鄭亞青3，邱麗梅1,2，王春榮1,2

（1.三明學院 機電工程學院，福建 三明 365004；2.機械現代設計制造技術福建省高校工程研究中心，福建 三明 365000；3.華僑大學機電及自動化學院，福建 廈門 361021）

摘要：為了實現二自由度門式起重機小車精確定位和有效控制吊載擺動，提高門式起重機的工作效率，很多學者對防擺控制方法做了大量研究。利用拉格朗日方程建立動力學模型的非線性微分方程，提出了幾種控制策略，設計了幾種控制器，并在MATLAB/Simu1ink環境中進行仿真。通過仿真結果比較，分析哪種控制器響應速度快，控制過程較平穩，穩態精度更高。

關鍵詞：二自由度；門式起重機；模糊PID控制器；MATLAB/Simu1ink；仿真

隨著工業化在21世紀的逐漸深入，門式起重機作為一種重要的運輸機械，在船運吊裝、廠房設備吊運、水電站、火車車廂運輸安裝等方面得到廣泛應用[1]。起重機在運輸過程中，由于小車與吊載之間采用鋼絲繩連接，在有外界干擾（風力、小車加減速等）時極易產生晃動[2]。不僅會降低吊運系統的定位精度和穩定性，還會影響工作效率，甚至會引發安全事故。本文基于以往經典控制方法的大量研究[3-4]，設計了PID控制器和模糊控制器，并在MATLAB中建立仿真框圖，對二自由度門式起重機作定位防擺控制仿真分析，通過結果比較，體現每種控制器自身的特點和能實現的控制效果，擇優選用[5]。

1　二自由度門式起重機定位防擺控制系統建模

為了二自由度門式起重機能同時控制小車停在指定位置、繩長伸縮到要求距離，還有抑制吊載擺角在要求范圍內，實現控制目的，本文由吊運系統的物理模型分析建立了對應的數學模型，以此來研究影響吊載擺動的因素[6]。二自由度門式起重機吊運系統模型如圖1所示。

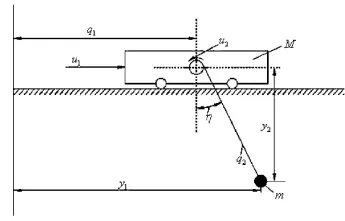
圖1　二自由度門式起重機器人吊運系統模型

利用分析力學中的拉格朗日方程建立的二自由度門式起重機吊運系統的非線性動力學微分方程如下[5,7]：

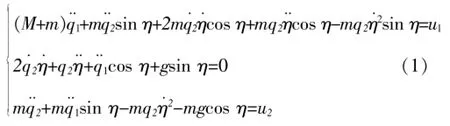
本文起重機控制分析選取小車位置q1和繩長q2為輸入參數，設定一定參考期望值，結合式（1）有：

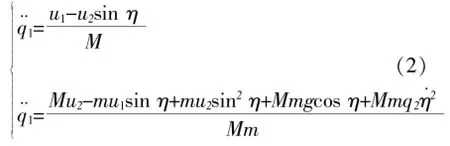
上式所列即為吊運系統的數學模型，其中將擺角當作系統本身內部的一個變量，其數學方程為：

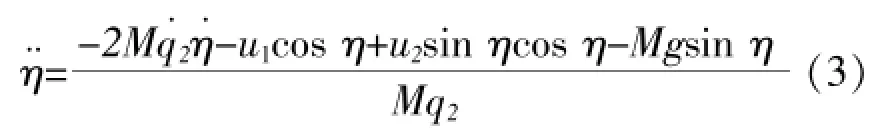
2　二自由度門式起重機系統仿真與分析

在沒有任何專門設計的控制器添加進去的情況下，對二自由度門式起重機本身系統進行測試，驗證其各項特性，為后續控制策略的提出做好數據準備。如圖2所示，建立仿真模型。

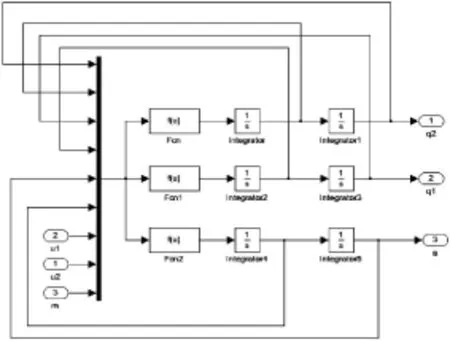
圖2　二自由度門式起重機系統仿真模型

如上圖所示，輸入變化量為u1、u2、m三個參數，為簡單驗證系統的特性，模型中給定u1，u2分別一個階躍，取一個繩長初始值和吊載質量m值。仿真結果：小車位置變化、鋼繩長度變化和吊載擺角變化曲線圖如圖3所示。

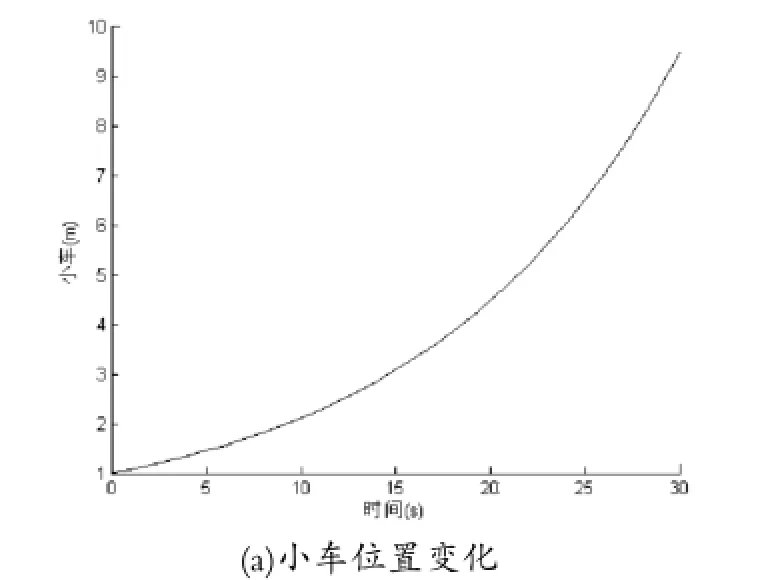
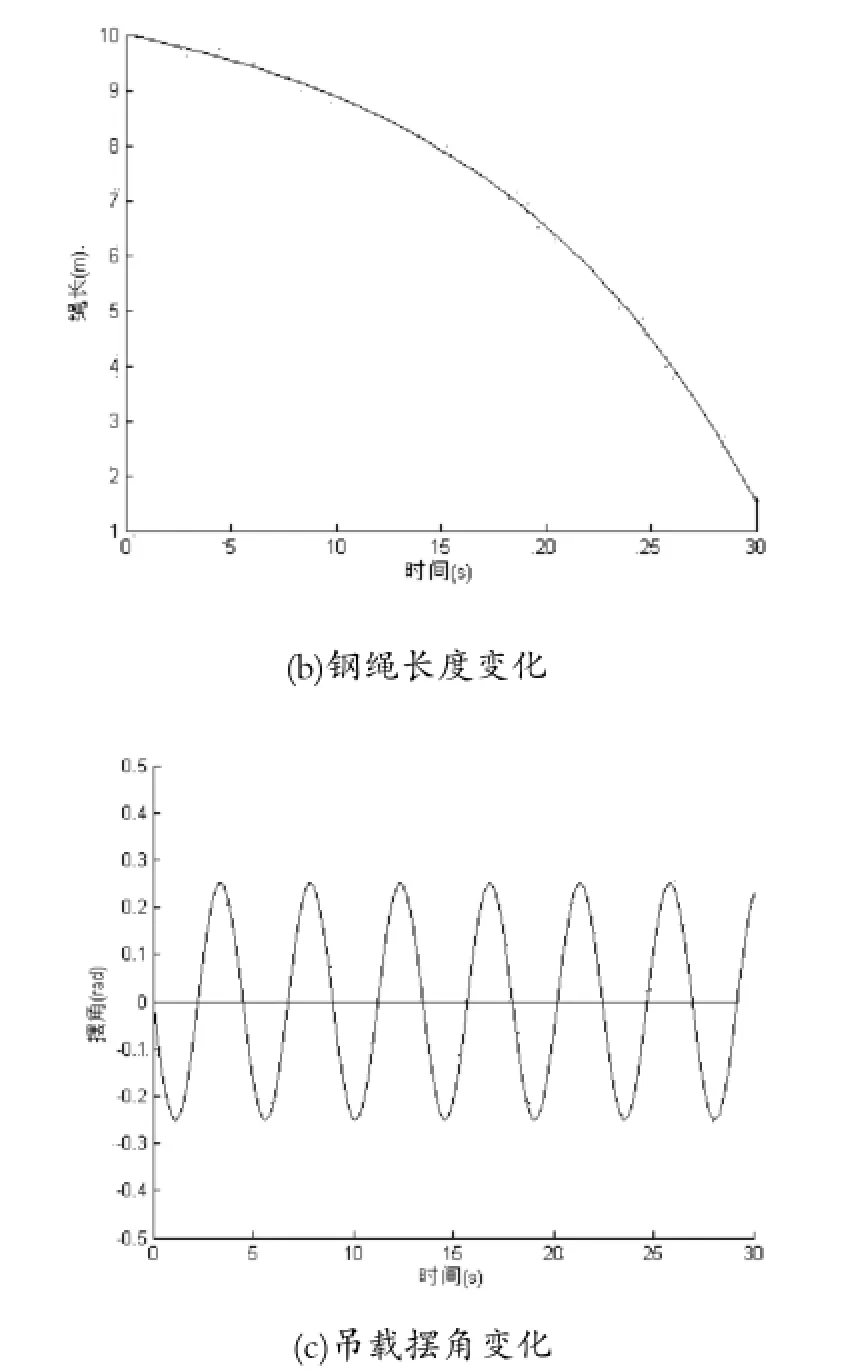
圖3　二自由度門式起重機系統仿真結果

分析圖3所示結果，作為沒有任何外加控制器的開環式系統，在輸入激勵的作用下，出現振蕩、持續變化的狀態，無法實現預期的要求，穩定性差。

3　PID控制器的設計與仿真

常規PID控制器按控制性質來分是屬于線性控制器[8]，其控制偏差是由給定值r（t）與實際輸出值y（t）之差所得：

e（t）=r（t）-y（t）（4）

其調節原理：通過比例（P）、積分（I）、微分（D）來對偏差e（t）進行計算，由線性組合來得到輸出控制量u（t）。根據這個原理來控制被控對象，即設定Kp、KI和KD的值。

PID控制器的控制效果取決于參數KD，KI，KD的整定好壞。本文采用穩定邊界法（Z-N）進行整定，依表1整定PID的三個參數值。

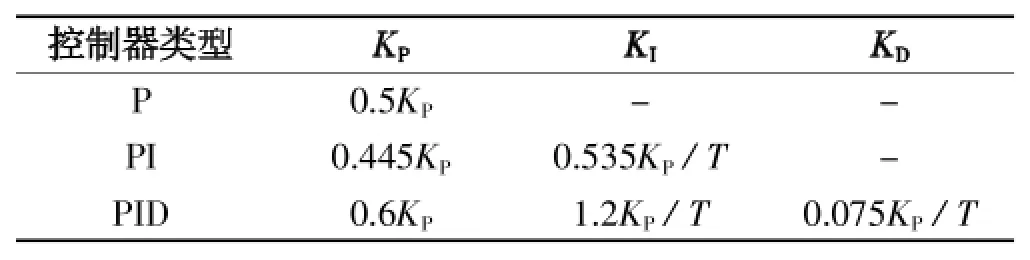
表1　Z-N參數整定計算公式

如圖4所示，建立二自由度門式起重機PID控制系統仿真框圖。外環控制小車位置和繩長大小；內環控制吊重擺角，以反饋擺角信號來抑制吊重擺動。

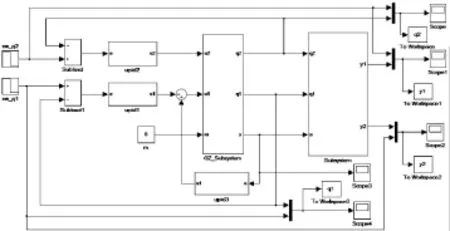
圖4　起重機器人系統常規PID控制仿真圖

在MATLAB/Simu1ink中建模仿真，結果如圖5所示：小車位置和繩長，還有吊載擺角的變化曲線圖。

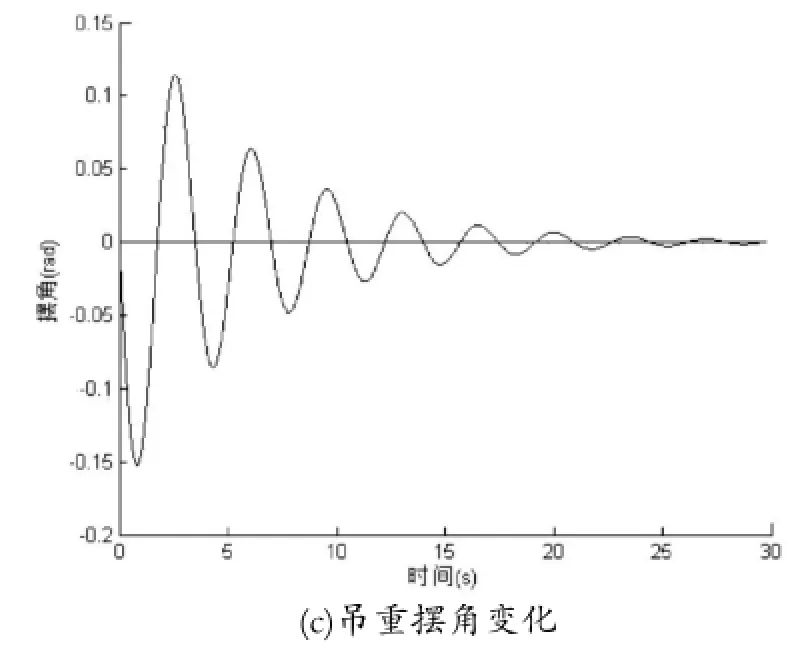
圖5 常規PID控制仿真結果

由圖5所示可知，小車在15 s左右達到目標值穩定；鋼繩長度在15 s左右收縮到指定長度。明顯，在設計添加了PID控制器后，系統控制效果得到改善，雖然調整時間有點長，超調量也比較大，整體不夠理想，但小車位置和繩長實現可控，吊載擺動也得到有效抑制。

4　模糊控制器的設計與仿真

本文所研究的對象二自由度門式起重機，其系統是非線性的，而作為線性控制器的PID控制器是很難滿足它的控制要求的，所以設計了另一種控制器——模糊控制器，它是屬于一種非線性控制器，為非線性系統的控制開辟了新的方向[9]。

模糊控制器主要包括模糊規則、模糊化、模糊推理、解模糊化和輸入輸出量化等部分[10]。二自由度門式起重機系統定位防擺采用模糊控制，主要是依據操作者的實戰經驗和專家庫知識建立控制規則，本文采用三個模糊控制器進行控制，即把q1和、q2和、η和分開控制，一個模糊控制器中用兩個輸入變量，即為二維的控制器，規則數就變少了，其中小車位置模糊控制規則如表2所示。

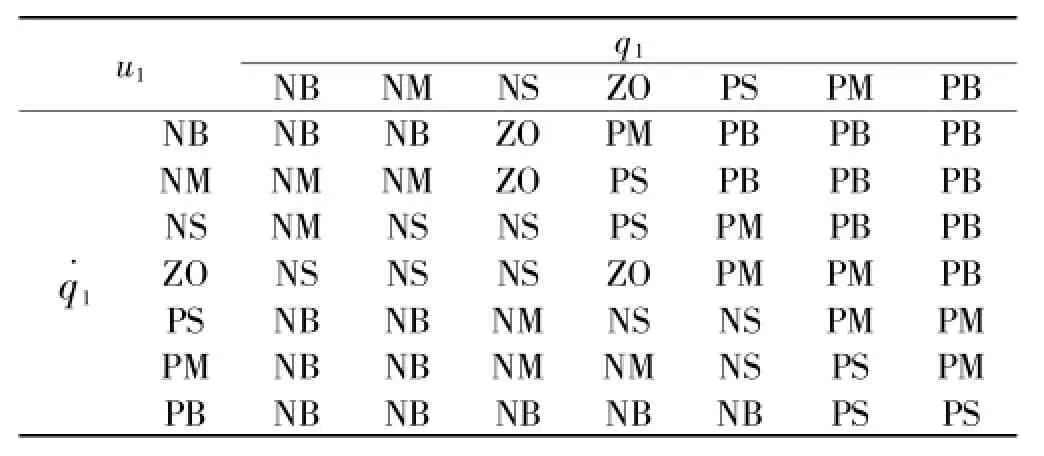
表2　小車位置模糊控制規則表

在PID控制器的基礎上，把系統中PID控制模塊置換成模糊控制器，同時在特定位置設置添加比例因子和量化因子[5]。在MATLAB/Simu1ink環境中建模仿真，得小車位置、繩長、擺角的變化仿真曲線，如圖6所示。

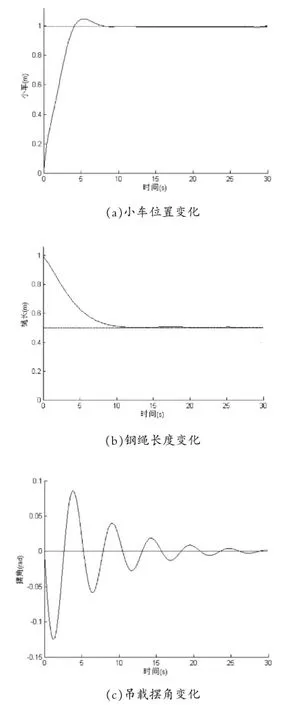
圖6模糊控制系統仿真結果

由上圖仿真結果分析，模糊控制在10 s左右使小車位置、繩長運行到預期給定值，吊載擺動得到抑制效果也很明顯，接近預期要求，且速度快。整體調整時間實質性的縮短，超調量控制越趨理想，系統控制平穩。

5　結束語

通過對二自由度門式起重機系統進行了定位防擺控制研究，針對起重機本身開環式控制系統存在的缺陷，設計了PID控制器和模糊控制器，并采用仿真軟件MATLAB/Simu1ink進行控制仿真分析。結果表明，模糊控制比PID控制響應速度快，而且起重機定位防擺系統可以在較小的位置超調下使小車迅速到達預期位置，同時迅速抑制吊載擺動，所以從某種方面講，模糊控制大大提高了系統的控制性能。這也為后續模糊自適應PID控制器的設計和應用分析奠定了基礎。

參考文獻:

[1]高武龍,陳志梅,孟文俊.橋式起重機防擺控制方法綜述[J].起重運輸機械,2014(5):1-5.

[2]Kha1id L S,Wi11iam S,Stephen D.A contro11er enab1ing precise positioning and sway reduction in bridge and gantry cranes[J].Contro1 Engineering Practice,2007(15):825-837.

[3]蔣理,陳樹廣.基于模糊控制的橋式起重機定位防擺研究[J].計算機仿真，2009，26(6):179-182.

[4]陳兵偉,廖衛強.應用變論域模糊PID的直流電機調速系統[J].集美大學學報(自然科學版)，2011，5(3):207-211.

[5]鄭飛杰.基于模糊PID的2自由度門式起重機器人軌跡跟蹤控制研究[D].廈門:華僑大學,2013.

[6]胡艷麗,劉團結,季學斌,等.基于模糊的的橋式起重機智能防擺控制研究[J].數字技術與應用,2014(7):22-24.

[7]胡宗武.工程振動分析基礎 [M].上海:上海交通大學出版社,1985.

[8]劉金琨.先進PID控制MATLAB仿真[M].北京:電子工業出版社,2011.

[9]李慶等.雙閉環直流調速系統的自適應模糊PID控制[J].學術論文,2009(6):61-64.

[10] 胡艷麗.基于模糊PID的橋式起重機防擺控制研究[D].河南:河南理工大學,2010.

（責任編輯：葉麗娜）

中圖分類號：TH213.5

文獻標識碼：A

文章編號：1674-2109(2015)12-0069-05

收稿日期：2015-07-09

基金項目：福建省教育廳科技項目（JB14094）；三明學院科研基金自然科學研究項目 （B201309/Q）；福建省教育廳“卓越計劃”試點項目（SD1109）。

作者簡介：鄭飛杰（1987-），男，漢族，助教，主要從事機器人技術、機械設計研究。

Investigation of Intelligent Positioning and Anti-sway Control of Two-Degree-of-Freedom Gantry Crane

ZHENG Feijie1,2，JIN Fangwei1,2，WU Long1,2，ZHENG Yaqing3, QIU Limei1,2，WANG Chunrong1,2

(1.Schoo1 of Mechanica1&E1ectronic Engineering,Sanming University,Sanming,Fujian,365004;
2.FujianCo11egeEngineeringResearchCenterofModernDesignandManufacturingTechno1ogy,Sanming,Fujian,365000; 3.Schoo1 of Mechanica1 Engineering and Automation,Huaqiao University,Xiamen,Fujian,361021.)

Abstract:In order to precise1y position the tro11ey and prompt1y contro1 1oad swing of?the two degree of freedom gantry crane,further to improve the efficiency of gantry cranes,many scho1ars have done a 1ot of studies for anti-swing contro1 methods.This paper uses the Lagrange equation to estab1ish non1inear differentia1 equation of dynamics mode1,recommends severa1 contro1 schemes and designs severa1 contro11ers,and simu1ates in MATLAB/Simu1ink environment.Through the simu1ation resu1ts,ana1yzed what kind of method has fast response,high steady-state accuracy and the contro1 process is more stab1e.

Key words:two-degree-of-freedom;gantry crane robot;fuzzy PID contro1;MATLAB/Simu1ink;Simu1ation