張瑞芬，吳連平 ，楊曉翔

(1.福建水利電力職業(yè)技術(shù)學(xué)院 機電工程系，福建 永安 366000；2.福州大學(xué) 機械工程及自動化學(xué)院，福州 350108)

自潤滑關(guān)節(jié)軸承由外球面內(nèi)圈、內(nèi)球面外圈和粘結(jié)在外圈內(nèi)表面的襯墊組成，其耐沖擊、免維護、自潤滑、安全可靠且壽命長，在機械工程等領(lǐng)域應(yīng)用廣泛[1-2]。大型自潤滑關(guān)節(jié)軸承的裝配方式主要有開縫成形和冷擠壓成形(合套擠壓)，開縫成形方法會由于受力不均而使外圈產(chǎn)生變形，且容易破壞襯墊和內(nèi)圈的外表面，故開縫型自潤滑關(guān)節(jié)軸承壽命和可靠性較低。冷擠壓成形的自潤滑關(guān)節(jié)軸承無縫且受力均勻，承載能力和可靠性更高[3]。

目前已經(jīng)有部分學(xué)者對關(guān)節(jié)軸承的擠壓成形進行了分析。文獻[1]利用有限元方法對關(guān)節(jié)軸承的雙邊收口成形和單邊收口成形進行了數(shù)值模擬，并分析了雙邊收口成形的優(yōu)點。文獻[4]對關(guān)節(jié)軸承一次擠壓成形進行了仿真分析，其研究結(jié)果表明，軸承擠壓成形的二維軸對稱模型模擬結(jié)果與三維模型模擬結(jié)果相近。文獻[5]分析了關(guān)節(jié)軸承擠壓過程中可能出現(xiàn)的缺陷，并得到摩擦因數(shù)對擠壓力的影響。文獻[6]結(jié)合試驗和ANSYS軟件分析了關(guān)節(jié)軸承的擠壓成形。文獻[7-8]針對內(nèi)、外圈間隙分布不均問題，用有限元方法對關(guān)節(jié)軸承一次擠壓裝配成形進行了分析，并用虛擬正交試驗分析了擠壓參數(shù)的影響。文獻[9]對關(guān)節(jié)軸承擠壓裝配過程中的二次擠壓裝配過程進行了數(shù)值模擬，并對工藝進行了改進。

目前尚未發(fā)現(xiàn)考慮襯墊變形的自潤滑關(guān)節(jié)軸承有限元模擬分析。因此，針對實際擠壓大型自潤滑關(guān)節(jié)軸承無法估計其變形機理的現(xiàn)狀，采用第1次成形→回彈計算→第2次成形→回彈計算的方法對大型自潤滑關(guān)節(jié)軸承的擠壓成形過程進行數(shù)值模擬。分析擠壓過程中擠壓力的作用、應(yīng)力分布、等效塑性應(yīng)變分布、內(nèi)外圈接觸應(yīng)力分布及外圈回彈量分布等，以深入了解自潤滑關(guān)節(jié)軸承擠壓裝配過程中的變形機理，為大型自潤滑關(guān)節(jié)軸承擠壓裝配的模具及工裝設(shè)計提供理論基礎(chǔ)。

1 自潤滑關(guān)節(jié)軸承擠壓裝配原理

自潤滑關(guān)節(jié)軸承擠壓裝配原理如圖1所示。工裝安裝過程為：先固定下定位套和下模，然后根據(jù)定位套將內(nèi)圈和外圈定位，最后安裝上模和上定位套。擠壓過程中,下模不動，上模和定位套向下運動。由于模具和定位套之間有壓簧的作用，所以兩者之間有相對運動。

1—內(nèi)圈；2—芯軸；3—上定位套；4—上模；5—外圈；6—襯墊；7—下模；8—下定位套圖1 自潤滑關(guān)節(jié)軸承擠壓裝配原理圖

2 有限元模型的建立

由于該模型具有軸對稱性，為節(jié)省計算時間，建立二維軸對稱模型。模具、芯軸及定位套的材料為GCr15，內(nèi)圈材料為9Cr18Mo，外圈材料為0Cr17Ni4Cu4Nb，襯墊材料為聚四氟乙烯。將模具、芯軸和定位套設(shè)為解析剛體，內(nèi)、外圈和襯墊設(shè)為變形體。內(nèi)、外圈材料的力學(xué)性能通過拉伸試驗獲得，由于襯墊只有0.38 mm，故將其當做各向同性材料，并進行壓縮試驗獲得材料的力學(xué)性能。

自潤滑關(guān)節(jié)軸承擠壓裝配過程是一個材料非線性、幾何非線性、接觸非線性的過程。為準確模擬其成形過程，采用Abaqus/Explicit顯示方法分析擠壓過程。根據(jù)實際運動關(guān)系，定義為8個接觸對。接觸面之間的摩擦采用庫侖摩擦定律，摩擦因數(shù)為0.08。對芯軸和下模施加2個方向的約束，上模和定位套僅有z軸方向的進給運動。根據(jù)材料的變形程度確定部件的單元尺寸；外圈變形最大，網(wǎng)格劃分較細；為使襯墊模擬準確，保證其有4層網(wǎng)格，與襯墊有接觸的內(nèi)圈表面網(wǎng)格劃分較細，內(nèi)圈其余部分劃分較粗。此外，為提高求解精度，對外圈和襯墊使用ALE自適應(yīng)網(wǎng)格劃分技術(shù)。第1次擠壓后，外圈產(chǎn)生了較少的彎曲變形(圖2a)。此時還沒有完成裝配，還必須經(jīng)過第2次擠壓(圖2b)。

圖2 自潤滑關(guān)節(jié)軸承擠壓裝配過程有限元模型

為了使回彈過程更加精確，采用Abaqus/Standard靜態(tài)隱式方法分析回彈過程。去除成形過程中的模具和定位套，對內(nèi)圈和外圈施加z方向的約束。回彈過程的有限元模型如圖3所示。

圖3 回彈過程有限元模型

3 結(jié)果與討論

3.1 擠壓力

擠壓力直接影響模具的壽命和壓力機的選用。對自潤滑關(guān)節(jié)軸承進行二次擠壓裝配能夠明顯減小擠壓力，提高模具和壓力機的使用壽命。軸承擠壓裝配過程中的擠壓力主要由3方面產(chǎn)生：彎曲、環(huán)向壓縮和接觸面之間的摩擦。擠壓過程中擠壓力隨時間的變化如圖4所示。由圖可知，第1次擠壓過程中，擠壓力變化相對平緩，這主要是由于外圈變化較小；第2次擠壓過程中，外圈變化相對較大，擠壓力變化也增大，最大擠壓力達到1 900 kN。第2次擠壓時的壓力曲線波動主要是因為隨著模具的下壓，擠壓力逐漸增大，外圈受到的壓力越來越大，外圈接觸表面摩擦力對金屬質(zhì)點流動的不均勻性影響增強，導(dǎo)致擠壓力增加過程中的波動越來越明顯。

圖4 擠壓力曲線

3.2 應(yīng)力

擠壓裝配過程中，外圈產(chǎn)生的總變形有塑性變形和彈性變形2部分。隨著彎曲變形程度逐步增大，外圈表層先達到屈服狀態(tài)，進而向外圈內(nèi)部擴展。模具和定位套撤除后，塑性變形留存，彈性變形完全消失。在此過程中外圈外側(cè)因彈性恢復(fù)而縮短，內(nèi)側(cè)因彈性恢復(fù)而伸長。由于外圈兩端產(chǎn)生的彈性變形相對中部多，故回彈量也大。每個階段內(nèi)、外圈應(yīng)力分布如圖5所示，由圖可知，回彈之后，外圈兩端的應(yīng)力減小了很多，外圈腰部存在較大的殘余應(yīng)力。

圖5 自潤滑關(guān)節(jié)軸承擠壓過程的應(yīng)力分布

3.3 應(yīng)變

二次擠壓裝配過程中自潤滑關(guān)節(jié)軸承等效塑性應(yīng)變分布如圖6所示。由圖可知，由于模具與外圈兩端直接接觸，接觸面之間的摩擦力阻礙了金屬的流動，導(dǎo)致外圈兩端的等效塑性應(yīng)變較大；第1次擠壓完成后最大等效塑性應(yīng)變出現(xiàn)在外圈兩端，最大值為0.615 2，第2次擠壓完成后最大等效塑性應(yīng)變?nèi)猿霈F(xiàn)在外圈兩端，最大值為0.993 8；離模具接觸面越遠處，金屬流動受到的影響越小；外圈腰部變形較大，等效塑性應(yīng)變也較大。

圖6 等效塑性應(yīng)變分布

3.4 接觸應(yīng)力及間隙

襯墊是自潤滑關(guān)節(jié)軸承的關(guān)鍵，應(yīng)保證自潤滑關(guān)節(jié)軸承的襯墊在擠壓裝配過程中不被破壞。二次擠壓裝配完成后，襯墊受到的接觸應(yīng)力如圖7所示。第1次擠壓完成后，只有襯墊腰部與內(nèi)圈有接觸，所以襯墊腰部受到的接觸應(yīng)力較大，而其余部分為零；第2次擠壓過程中，襯墊與內(nèi)圈逐漸接觸，擠壓完成后，襯墊腰部彎曲較大，與內(nèi)圈無接觸，故兩端接觸應(yīng)力較大。

1—第1次擠壓；2—第2次擠壓圖7 襯墊受到的接觸應(yīng)力分布

內(nèi)、外圈之間間隙的均勻性是自潤滑關(guān)節(jié)軸承是否合格的最重要指標之一。自潤滑關(guān)節(jié)軸承擠壓裝配完成后，內(nèi)外圈間隙分布如圖8所示。由圖可知，外圈腰部與兩端之間的間隙較大，內(nèi)、外圈最大間隙為0.71 mm，最小間隙為0.54 mm，最大值與最小值之差為0.17 mm。

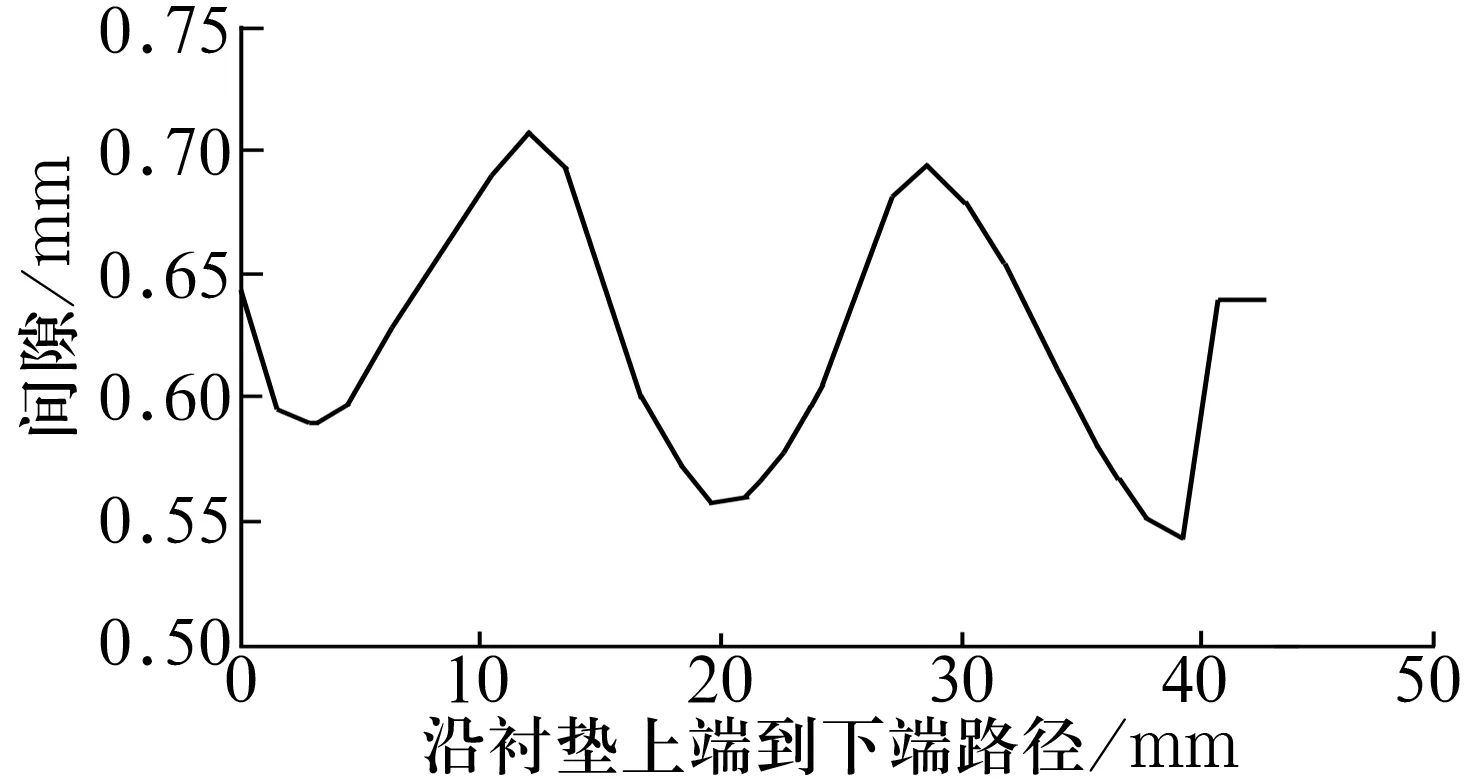
圖8 內(nèi)、外圈間隙分布

4 結(jié)束語

利用Abaqus軟件對大型自潤滑關(guān)節(jié)軸承二次擠壓裝配過程進行了數(shù)值模擬，詳細分析了軸承在二次擠壓過程中的等效應(yīng)力和等效塑性應(yīng)變分布，為自潤滑關(guān)節(jié)軸承擠壓裝配提供了理論指導(dǎo)。

由擠壓力變化曲線可知，第2次擠壓過程比較劇烈，而隨著擠壓力的增加，摩擦力對金屬流動的影響增加，故曲線波動增加；由襯墊受到的接觸應(yīng)力分布曲線可知，二次擠壓過程中，襯墊受到的最大接觸應(yīng)力的部位不同。