雙偏心球籠式等速萬向節的結構設計

石寶樞,徐建權

(1.浙江眾達傳動股份有限公司，浙江 金華 321025;2.萬向錢潮股份有限公司 等速驅動軸廠，杭州 311215)

符號說明

B0——星形套溝道中心至端面的距離，mm

Bj——偏心保持架總寬度，mm

Bj0——偏心保持架窗孔中心至端面的距離，mm

Bj1——偏心保持架內球面的軸向長度，mm

Bk——偏心保持架每個圓形窗孔的軸向寬度，mm

Bx——星形套溝道的軸向長度(星形套寬度)，mm

c——鋼球在溝道內沿徑向其中一個方向的位移量，mm

cz——鋼球在溝道內沿徑向2個方向的最大位移總量，mm

cmax——鋼球在溝道內沿徑向其中一個方向位移量的最大值，mm

D——星形套和鐘形殼的鋼球中心圓直徑，mm

D1——偏心保持架每個圓形窗孔的直徑，mm

Dg——鐘形殼溝道底部直徑，mm

Dj——偏心保持架內球面直徑，mm

Dk——鐘形殼最大外徑，mm

Dq——鐘形殼內球面直徑，mm

Dw——鋼球直徑，mm

dg——星形套溝道底部直徑，mm

dj——偏心保持架外球面直徑，mm

dq——星形套外球面直徑，mm

dz——傳動軸公稱直徑，mm

e——星形套、鐘形殼及偏心保持架的偏心距，mm

L——鐘形殼溝道的軸向長度，mm

L0——鐘形殼溝道中心至外端面的距離，mm

R——星形套和鐘形殼的鋼球中心圓半徑，mm

Rk——鐘形殼圓弧形溝道的截面半徑，mm

Rx——星形套圓弧形溝道的截面半徑，mm

K——星形套和鐘形殼的鋼球中心圓直徑系數

ε——偏心保持架的厚度加強值，mm

θ——星形套、鐘形殼及偏心保持架的偏心角，(°)

α——輸入軸相對于輸出軸的轉角，(°)

α1——偏心保持架相對于輸出軸(鐘形殼)的轉角，(°)

α2——偏心保持架相對于輸入軸(星形套)的轉角,(°)

αmax——輸入軸相對于輸出軸轉角的最大值，(°)

球籠式等速萬向節的主要功能為： 1)連接輸入軸和輸出軸； 2)將輸入軸的運動和轉矩傳遞到輸出軸。為使兩軸在極限轉角范圍內的任一位置均可隨時、精確、可靠的定位，傳統結構的球籠式等速萬向節通過與輸入軸連接的星形套和與輸出軸連接的鐘形殼兩組與相應球面偏心的溝道實現,故該萬向節的內、外球面同心的球籠式保持架只能起引導兩軸轉角的功能。此類球籠式等速萬向節不僅結構復雜，而且各種關聯的結構要素相互制約，設計、加工及檢測難度大；反之，若星形套和鐘形殼的溝道同心，而內、外球面非同心(偏心)的球籠式保持架，亦可實現兩軸的定位。為此，創新設計了同樣可實現上述功能的產品——雙偏心球籠式等速萬向節。這是對傳統結構球籠式等速萬向節的重要拓展，文中給出了該等速萬向節的結構設計、主參數及尺寸的計算方法。

1 雙偏心球籠式等速萬向節結構特征

雙偏心球籠式等速萬向節工作部分的主要結構如圖1所示,由星形套、鐘形殼、偏心保持架和鋼球等組成。

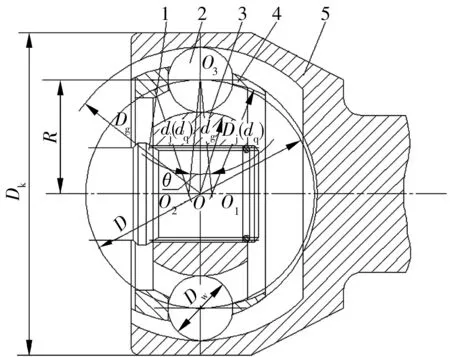
1—傳動軸(輸入軸)；2—鋼球；3—星形套(內溝道)；4—偏心保持架；5—鐘形殼(外溝道、輸出軸)圖1 雙偏心球籠式等速萬向節結構示意圖

結構特征：與輸入軸連接的星形套外球面與相應的偏心保持架內球面配合；與輸出軸連接的鐘形殼內球面與相應的偏心保持架外球面配合；偏心保持架內球面(星形套外球面)中心和外球面(鐘形殼的內球面)的中心分別置于圓形窗孔(即鋼球)中心的兩側，且內、外球面中心至圓形窗孔中心的距離(偏心距)均相等；用于傳力的鋼球一

般為6～8個(創新優化設計后鋼球數為7)；偏心保持架亦有相同數量且沿圓周方向均布的圓形窗孔，用于夾持鋼球、引導兩軸的轉角并定位，偏心保持架的每一圓形窗孔沿軸向方向的兩側壁(圓形窗孔的軸向寬度)均與相應的鋼球過盈配合，當兩軸轉角時，沿徑向方向上的每一圓形窗孔的直徑，確保了每一鋼球在相應的星形套和鐘形殼溝道內，沿徑向有足夠的活動空間。星形套和鐘形殼的溝道中心均與兩軸交點(偏心保持架圓形窗孔的中心)重合，在星形套外球面上，亦設計相同數量、沿圓周方向均布、素線為圓弧形、通過其溝道中心的截面形狀為圓弧形(或雙偏心圓弧形、橢圓形)的外溝道；同樣，在鐘形殼內球面上，亦設計相同數量、沿圓周方向均布、素線為圓弧形、通過其溝道中心的截面形狀為圓弧形(或雙偏心圓弧形、橢圓形)的內溝道；星形套和鐘形殼溝道均分別與相應的鋼球共軛接觸，當星形套(輸入軸)和鐘形殼(輸出軸)有一定角位移等復雜工況下，雙偏心球籠式等速萬向節仍能平穩、可靠、靈活、精確地傳遞運動和轉矩。

2 兩軸轉角時的運動機理

如圖1所示，設雙偏心球籠式等速萬向節的星形套和鐘形殼的溝道中心(兩軸交點)為O，偏心保持架內球面(星形套外球面)的中心為O1，偏心保持架外球面(鐘形殼內球面)的中心為O2。因偏心距相等(OO1=OO2=e)。顯然，星形套和鐘形殼的鋼球中心圓半徑(或直徑)亦相等。當星形套相對于鐘形殼繞兩溝道中心O轉角為α時，雙偏心球籠式等速萬向節的運動情形如圖2所示。

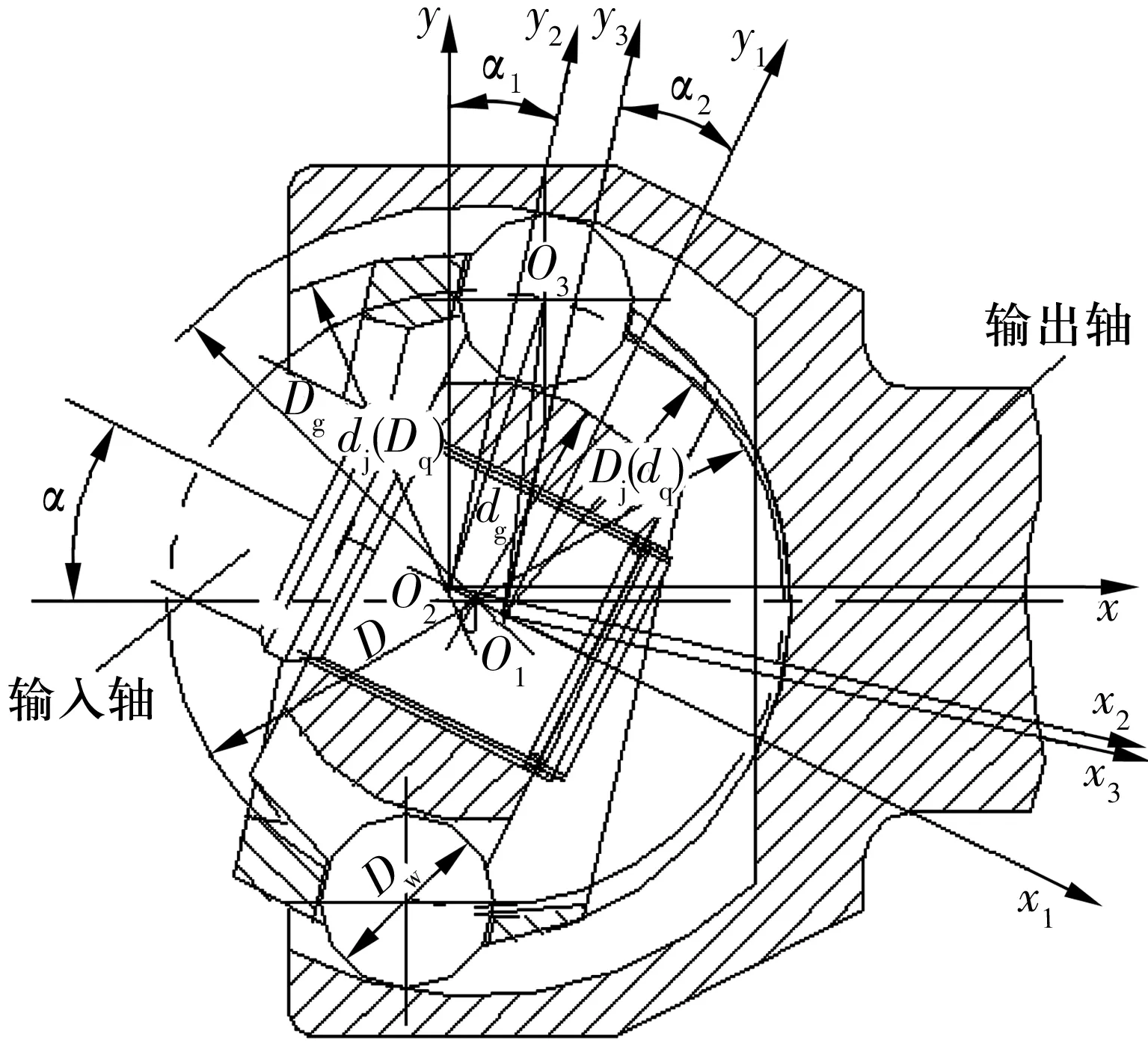
圖2 雙偏心球籠式等速萬向節的轉角

星形套的鋼球中心圓半徑為

(1)

鐘形殼的鋼球中心圓半徑為

(2)

2.1 坐標系的建立

通過偏心保持架的內、外球面，分別與相應的星形套外球面、鐘形殼內球面配合，引導并實現了雙偏心球籠式等速萬向節的星形套和鐘形殼均繞O點轉動。為便于對該萬向節的運動機理(等速傳動條件)進行系統、深入的分析，建立如下坐標系：

1)以O2為坐標原點，建立平面直角坐標系O2xy。

2)以O2為坐標原點，建立關于偏心保持架的平面直角坐標系O2x2y2。設星形套繞O相對于鐘形殼的轉角為α;偏心保持架繞O2順時針的轉角為α1。由坐標軸的旋轉得[1]

(3)

(3)式可轉化為[2]

(4)

3)以O1為坐標原點，建立關于星形套的平面直角坐標系O1x1y1。

4)以O1為坐標原點，建立關于偏心保持架的平面直角坐標系O1x3y3。若偏心保持架相對于輸入軸星形套的轉角為α2，由坐標軸的旋轉得

(5)

2.2 運動機理(等速傳動條件)

雙偏心球籠式等速萬向節各轉角的關系為

α1=α-α2。

(6)

沿圓周均布的每個鋼球在其相應的星形套和鐘形殼溝道內，沿徑向其中一個方向的位移為c，則鋼球中心O3在O2x2y2坐標系中的坐標分別為

x2=e；

該鋼球中心O3在O2xy坐標系中的坐標分別為

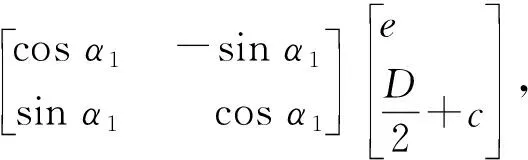
(7)

即

當星形套繞O轉角α時，設偏心保持架繞O1相對于星形套逆時針的轉角為α2，則鋼球中心O3在O1x3y3坐標系中的坐標分別為

x3=-e;

該鋼球中心O3在O1x1y1坐標系中的坐標分別為

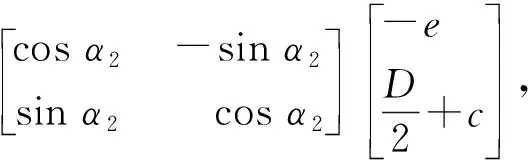
(8)

即

在兩軸極限轉角范圍內的任何情況下，雙偏心球籠式等速萬向節的每個鋼球均必須與相應的星形套和鐘形殼兩溝道同時相切。所以，其球心O3至兩溝道中心O的距離始終保持不變,距離為

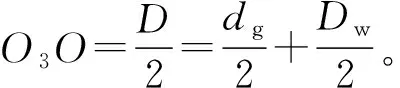
由(7)和(8)式得

(9)

(10)

由(9)式和(10)式得

α1=α2，

(11)

把(11)式代入(7)和(8)式得

y=y1。

(12)

因此，雙偏心球籠式等速萬向節的每個鋼球中心至星形套和鐘形殼的垂直距離均相等，可以保證該萬向節的等角速傳動。將(11)式代入(6)式得

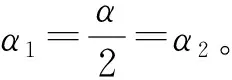
(13)

3 鋼球徑向位移的解析

根據雙偏心球籠式等速萬向節的結構特征和兩軸轉角時的運動機理，可對該萬向節沿圓周均布的每個鋼球在其相應的星形套和鐘形殼溝道內，沿徑向(偏心保持架圓形窗孔的長度方向)其中一個方向的位移量進行求解。

將(6)式和(13)式分別代入(9)式或(10)式，整理后可得

(14)

將α=αmax代入(14)式，得徑向位移量的最大值為

(15)

雙偏心球籠式等速萬向節的最大轉角,即星形套相對于鐘形殼繞兩軸的交點(溝道中心)沿順時針、逆時針2個方向轉角的極限值為

αmax-(-αmax)=2αmax,

顯然，該萬向節的每個鋼球在其相應的星形套和鐘形殼溝道內，沿徑向(偏心保持架圓形窗孔的直徑方向)2個方向的最大位移量為

cz=2cmax，

(16)

將(15)式代入(16)式得

4 結構主參數及零件主要尺寸的設計與計算

4.1 結構主參數的設計與選取

4.1.1 鋼球數

同傳統結構的球籠式等速萬向節一樣，鋼球數一般為6～8個。經優化設計，鋼球數為7是這類萬向節結構設計的唯一、最佳的選擇[3]。

4.1.2 鋼球直徑

同傳統結構的球籠式等速萬向節一樣，雙偏心球籠式等速萬向節的鋼球直徑為[4]

(18)

4.1.3 傳動軸公稱直徑

根據球籠式等速萬向節的規格、外形尺寸及載荷，對傳動軸的直徑進行可靠性設計和優化設計。根據可靠性和優化設計的結果，雙偏心球籠式等速萬向節傳動軸的公稱直徑為

dz≥1.4Dw。

(19)

4.1.4 鋼球中心圓直徑

雙偏心球籠式等速萬向節星形套和鐘形殼的鋼球中心圓直徑為

D=K(Dk+dz)，

(20)

式中：K=0.54～0.55。

4.1.5 偏心距

雙偏心球籠式等速萬向節的偏心距,即偏心保持架圓形窗孔中心至內、外球面中心(鐘形殼或星形套溝道中心至內、外球面中心)的距離。由圖1可知，該偏心距為

(21)

式中：θ=11°～12°。

4.2 偏心保持架的內、外球面直徑

偏心保持架的每個圓形窗孔與相應鋼球的接觸如圖3所示。由于當兩軸的轉角α=0時，偏心保持架每一圓形窗孔側壁的中點C與相應的鋼球接觸(相切)受力最均勻。所以，根據星形套及鐘形殼的鋼球中心圓直徑，即可設計計算偏心保持架的內、外球面直徑。

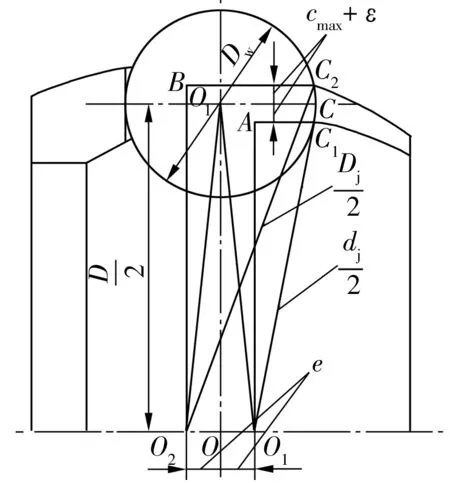
圖3 偏心保持架窗孔與鋼球的接觸

當兩軸的轉角達到最大值時，在內球面處，某圓形窗孔側壁與相應鋼球的切點為C1；在外球面處，該圓形窗孔側壁與相應鋼球的切點為C2。根據兩軸轉角的運動機理，理論上C1C=C2C=cmax，但為使偏心保持架每個圓形窗孔與相應的鋼球充分接觸，應適當增加其厚度，以提高承載能力，延長使用壽命。實際設計的偏心保持架的厚度應確保當兩軸的轉角達到最大值時，偏心保持架的每個圓形窗孔與相應的鋼球均能很好地接觸。取

C1C=C2C=cmax+ε,ε=0.03Dw。

由幾何關系得

由此，偏心保持架內球面直徑為

(22)

將(15)式代入(22)式得

(23)

式中：αmax=45°～47° 。

同理，得

偏心保持架外球面直徑為

(24)

將(15)式代入(24)式，得

(25)

4.3 鐘形殼主要尺寸

4.3.1 內球面直徑

由于鐘形殼內球面與相應的偏心保持架外球面配合。顯然，兩者直徑的公稱值應相等，即

Dq=Dj，

(26)

將(23)式代入(26)式，得鐘形殼內球面直徑為

(27)

4.3.2 溝道截面半徑

鐘形殼通過其溝道中心的溝道截面形狀，主要有圓弧形、雙偏心圓弧形和橢圓形等結構形式。圓弧形溝道截面的圓弧半徑為

Rk=0.505Dw。

(28)

4.3.3 溝道底部直徑

由圖1可知，鐘形殼圓弧形溝道的底部直徑應等于鋼球中心圓直徑與相應的鋼球直徑之和。即

Dg=D+Dw。

(29)

4.3.4 溝道的軸向長度

鐘形殼溝道的軸向長度取決于兩軸的最大轉角。當兩軸為最大轉角時，為使該溝道與鋼球充分接觸，該溝道應有一軸向加長值。鐘形殼溝道的軸向長度為

(30)

4.3.5 溝道中心至外端面的距離

由于雙偏心球籠式等速萬向節的兩軸是繞溝道中心旋轉,所以鐘形殼的溝道中心應與該溝道的軸向長度中心重合。則鐘形殼的溝道中心至外端面的距離為

(31)

將(30)式代入(31)式，得

(32)

4.4 星形套主要尺寸

4.4.1 外球面直徑

由于星形套外球面與相應的偏心保持架內球面配合,故兩者直徑的公稱值應相等，即

dq=Dj。

(33)

將(25)式代入(33)式，得星形套外球面直徑為

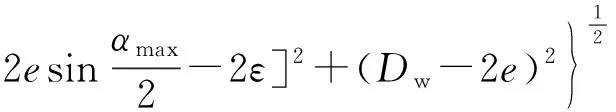
(34)

4.4.2 溝道截面半徑

同鐘形殼一樣，星形套通過其溝道中心的圓弧形溝道的截面半徑為

Rx=0.505Dw。

(35)

4.4.3 溝道底部直徑

由圖1可知，星形套圓弧形溝道的底部直徑應等于鋼球中心圓直徑減去相應的鋼球直徑。即

dg=D-Dw。

(36)

4.4.4 寬度

星形套寬度(溝道的軸向長度)為

(37)

4.4.5 溝道中心至端面的距離

星形套的溝道中心應與其寬度中心重合,故星形套的溝道中心至任一端面的距離為

(38)

將(37)式代入(38)式，得

(39)

4.5 偏心保持架其他主要尺寸

4.5.1 內球面軸向長度

由于偏心保持架內球面與相應的星形套外球面配合，所以偏心保持架內球面的軸向長度應與相應的星形套寬度相等，即

Bj1=Bx，

(40)

將(37)式代入(40)式，得偏心保持架內球面的軸向長度為

(41)

4.5.2 總寬度

偏心保持架總寬度

Bj=Bj1+2e，

(42)

將(41)式代入(42)式，得

(43)

4.5.3 窗孔中心至端面的距離

偏心保持架的每個圓形窗孔中心均處于其寬度中心，故偏心保持架圓形窗孔的中心至任一端面的距離為

(44)

將(43)式代入(44)式，得

(45)

4.5.4 圓形窗孔的軸向寬度和直徑

偏心保持架圓弧窗孔的結構如圖4所示。偏心保持架每個圓弧形窗孔的軸向方向與相應的鋼球系過盈配合，所以每個圓弧形窗孔的軸向寬度與相應鋼球的公稱直徑應相等。即

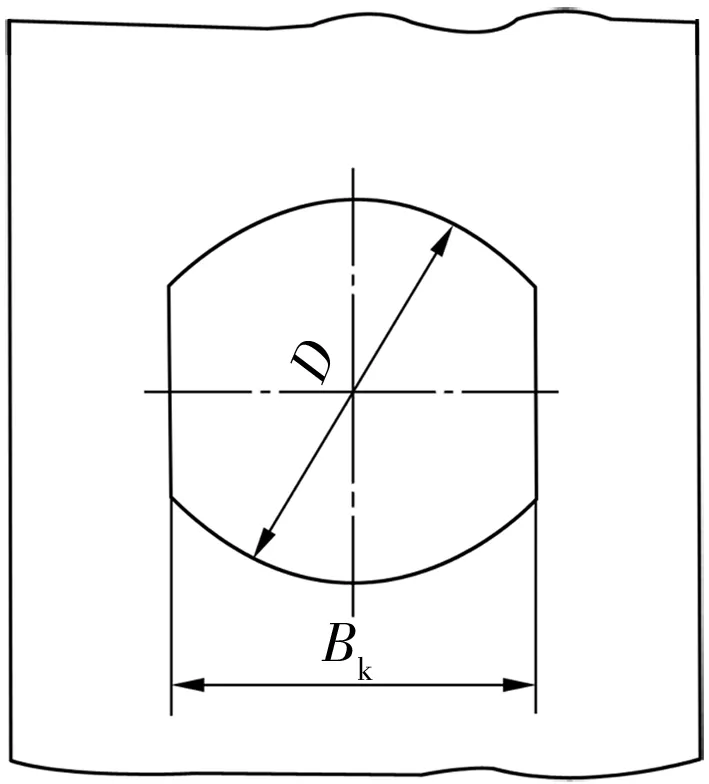
圖4 偏心保持架的窗孔

Bk=Dw。

(46)

雙偏心球籠式等速萬向節在兩軸轉角時，沿圓周均布的每個鋼球，在相應的星形套和鐘形殼溝道內不僅沿軸向滾動，在徑向上，還要沿偏心保持架圓形窗孔的直徑方向移動。顯然，每個圓弧窗孔的直徑應等于相應的鋼球直徑(圓弧形窗孔的軸向寬度)與該鋼球在溝道內沿徑向2個方向的位移總量之和。即

D1=Dw+cz，

(47)

將(17)式代入(47)式，得

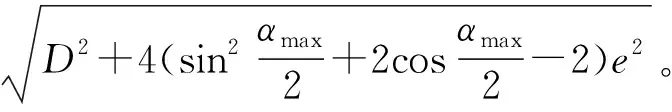
(48)

4.6 設計與計算實例

某雙偏心球籠式等速萬向節，已知Dk=90 mm,αmax=47°。試設計計算其結構主參數。

根據雙偏心球籠式等速萬向節結構主參數及零件主要尺寸的設計與計算方法，把已知條件分別代入上述相應公式，可分別計算出相應的結構主參數及零件的主要尺寸。具體結果見表1。

表1 結構主參數計算結果

5 結束語

探討了創新設計的雙偏心球籠式等速萬向節的幾何結構、運動機理、結構主參數及零件主要尺寸的設計與計算方法。未涉及結構主參數及零件主要尺寸計算結果的取值精度、公差與配合的選擇。該運動機理與設計計算方法，是對等速萬向節基礎理論和結構設計的重要突破。該雙偏心球籠式等速萬向節，具有結構新穎、合理、緊湊；工作平穩、靈活、精確、可靠、耐沖擊、傳遞轉矩大；工藝性好，便于設計、加工及檢測等突出優點。