基于ELM的成本預測方法實證檢驗

朱 正，陶 嵐

0 引言

會計成本預測一直是學術界比較關心的問題，不論企業(yè)的大小，在對企業(yè)生產，特別是進行新的產品研發(fā)和上線過程中，會計成本預測成為企業(yè)決策的重要參考，因此，關于會計成本預測也是學界一直研究的熱點問題。通過對以往關于會計成本預測方法的研究和總結可以看出，首先，會計成本預測過程中影響因素眾多，各因素之間的關聯(lián)性很強，具有很強的非線性關系，因此簡單的線性預測方法是不可行的，必須利用能有效反映各因素之間非線性關系的非線性預測方法，對會計成本預測的精度才會高；其次，所使用的預測方法，有人工神經網絡方法，有模糊粗糙集成本預測方法，這些方法雖然能有效提升成本預測的精度，但是其共同特點是計算復雜，計算量大，不便于實際的應用。因此，構建一套新的簡單、快速、又能反映會計成本預測中非線性關系是后期成本預測方法的主要研究和發(fā)展趨勢。本文結合最新研究成果，利用最新提出的一種基于單隱層前饋神經網絡的極限機器學習法（ELM），該方法既能反映出成本預測中各因素之間的非線性關系，還能有效提升成本預測速度，結構簡單，因此，基于ELM的成本預測是最適合作為成本預測的模型。

1 極限學習機（ELM）建模原理

最近基于神經網絡提出的一種新的極限學習機（ELM)通過隨機產生隱曾結點參數(shù),然后利用得到的外權決定輸出，大大簡化了傳統(tǒng)神經網絡復雜的迭代過程，使得在保證高精度擬合的基礎上大大簡化了運算過程。下面給出極限學習機的建模原理。

對N個任意確定樣本 (xi，yi)，其中 xi=[xi1，xi2，…xin]Τ∈Rn，yi=[yi1，yi2，…yim]Τ∈Rm，標準的單隱層前饋神經網絡(SLFNs)學習算法有個隱含結點，選取適當?shù)募せ詈瘮?shù)g(x)，則根據(jù)神經網絡的結構原理結構圖為：

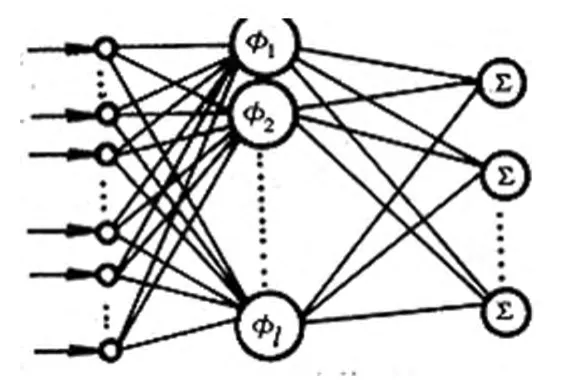
圖1 單隱層前饋神經網絡(SLFNs)結構圖

其對應的神經網絡的數(shù)學模型描述如下：

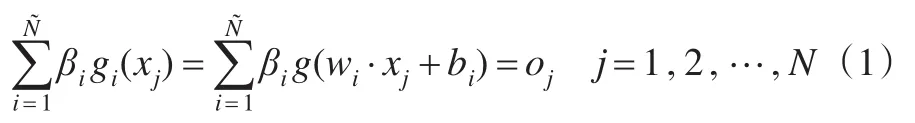
其中 wi=[wi1，wi2，…win]Τ∈Rn是第 i個隱含層結點和所有n個輸入結點的連接權重向量，βi=[βi1，βi2，…βim]Τ∈Rm是第 i個隱含結點和所有m個輸出結點的連接權重向量，并且常數(shù)bi是第i個隱含結點的閾值，其中wi·xj表示向量wi和向量xj的內積。

g(w1·x1+b1)β1+g(w2·x1+b2)β2+ …+g(w·x1+b)β=y1

g(w1·x2+b1)β1+g(w2·x2+b2)β2+ … +g(w·x2+b)β=y2

利用矩陣的形式將上面的方程進行簡寫，得到線性矩陣方程：

其中

H一般稱為神經網絡隱含層輸出矩陣，其中H的第i個列是第i個關于輸入x1，x2，…，xN的隱含層結點輸出。

為了訓練一個SLFNs，其實就是通過不斷的學習訓練，找到理想的向量和常數(shù)使得以下最優(yōu)化函數(shù)有解：

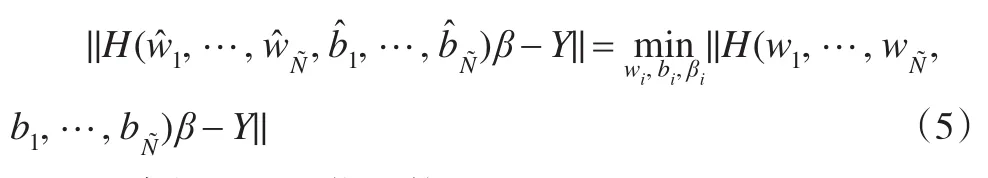
即求解以下最優(yōu)函數(shù)：

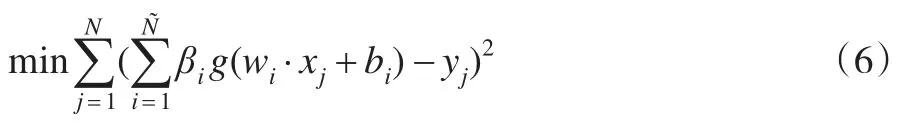
該函數(shù)的求解，通過證明，當給定加權向量wi和bi后，其最優(yōu)解等價對線性方程組Hβ=Y求解。考慮到樣本個數(shù)N和隱層結點數(shù)不同，因此，在對線性方程組Hβ=Y的求解過程中，可以采用廣義逆的方法進行求解。

2 基于ELM的成本預測算法設計

通過以上的分析可以看出，極限學習機是基于單隱層前饋神經網絡構建的預測模型，因此具有神經網絡的非線性特性，但是通過最終的推導可以看出，最終ELM方法在對隱層權重的求解簡化為對線性方程組的求解上，大大簡化了預測的計算速度，下面基于ELM的原理，給出基于ELM的會計成本預測算法設計過程。

設對某企業(yè)的會計成本進行預測，選擇L個時期內的企業(yè)成本歷史數(shù)據(jù)為：

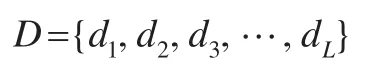
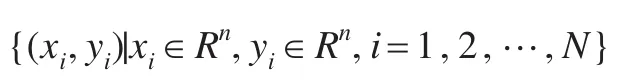
其中向量xi代表第i次隨機選擇成本歷史數(shù)據(jù)所對應的時間，而yi則是第i次隨機選擇成本歷史數(shù)據(jù)所對應的成本值。

③選定激活函數(shù)g(x)，計算隱含層輸出矩陣H。

⑤預測：選擇所要預測的時間，如預測未來p個時期內的企業(yè)會計成本數(shù)值，則選擇

x*=(L-n+p+1，…，L-2，L-1，L，L+1，L+2，…，L+p)將基于ELM的預測值為：

語言不是獨立的，是與社會文化相關的，因而語言表達方式存在差異。漢語是話題突出型語言，需說明的對象總是放在句子開頭處，采用隱性連貫，句子間沒有過多的連接詞，短句之間靠整個話題維系；而英語是主語突出型語言，常采用主語-謂語的句式，采用顯性連接，可用多種的連接手段表達時序和邏輯關系，復合長句是英語的一個主要特色。因此，漢英翻譯時須做好語序的調整和句型結構的轉換。

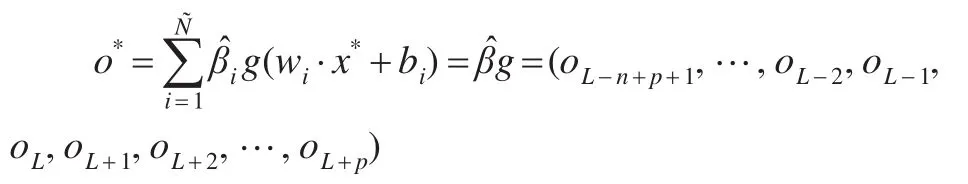
其中

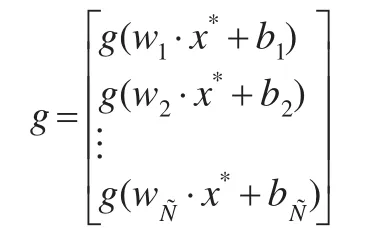
則oL+1，oL+2，…，oL+p就是利用ELM得到的未來 p個時期內的企業(yè)會計成本預測數(shù)值。

3 基于ELM的成本預測實證檢驗

在對企業(yè)成本預測過程中，必須選擇簡單可據(jù)操作性的預測方法。某企業(yè)為了對企業(yè)的成本進行監(jiān)測和控制，必須定期對企業(yè)成本進行預測，現(xiàn)在采集近20個時期的成本作為成本歷史數(shù)據(jù)，建立企業(yè)的成本預測模型，采集到的成本數(shù)據(jù)如表1所示。

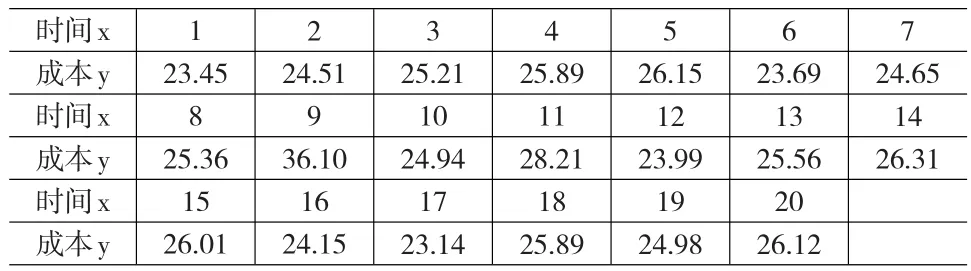
表1 某企業(yè)近20個時期內的成本預測數(shù)據(jù) （單位：十萬元）

首先構建訓練樣本集，在20組成本數(shù)據(jù)中，隨機選擇7組數(shù)據(jù)構成一個訓練樣本，共隨機產生50個訓練樣本構成訓練樣本集：

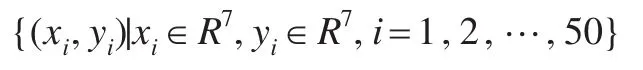
其中xi代表第i次隨機產生訓練樣本中的時間序列構成的向量，yi代表第i次隨機產生訓練樣本中的成本數(shù)值序列構成的成本向量，選取激活函數(shù)為高斯函數(shù)，即：

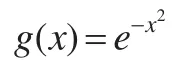
設定隱層結點個數(shù)為10個，隨機產生加權向量值，隨機給定偏置值bi（ i=1，2，…，10 ）為 ：b=(7.27，7.94， 1.36， 5.82， 2.97，4.15， 2.96， 6.83，4.54， 6.8)

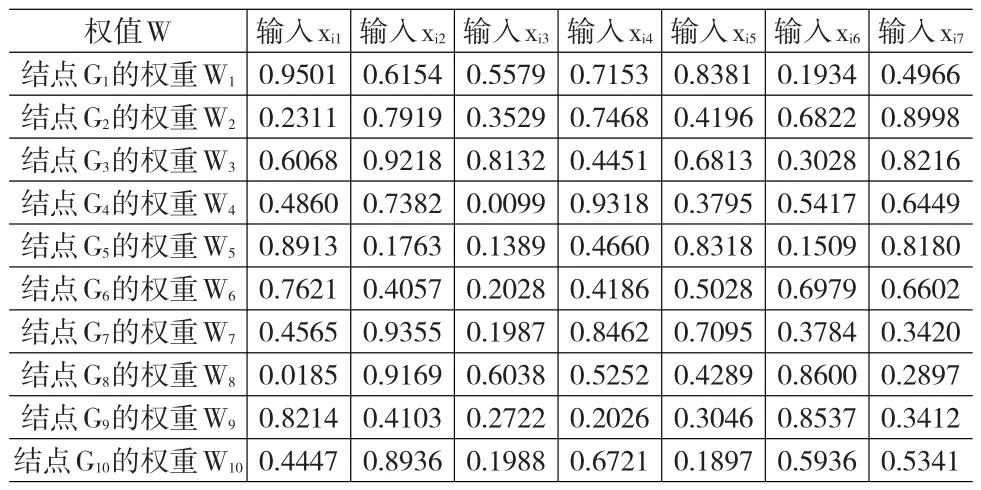
表2 隨機給出的加權向量矩陣

將隨機產生的50個樣本值 (xi，yi) ，(i=1，2，…，50)，隨機給定的隱含層結點和所有輸入結點的連接權重向量W（表2）、隱層結點偏置值b，激活函數(shù)g(x)=e-x2帶入下式：

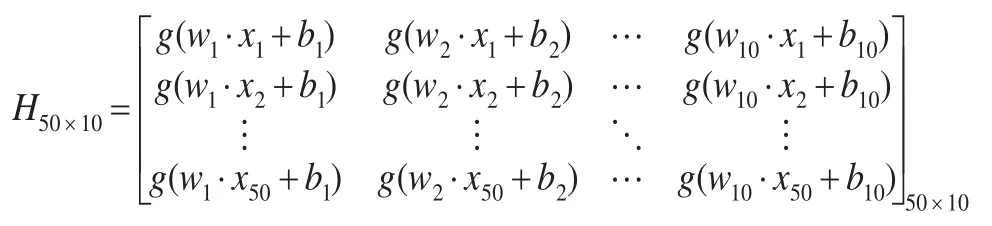
從而得到一個常數(shù)型的神經網絡隱含層輸出矩陣H50×10。將50個訓練樣本的輸出成本向量排列構成成本輸出矩陣：

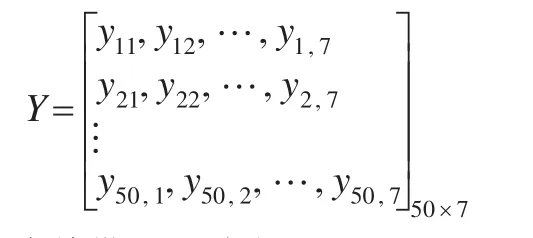
Hβ=Y

為了檢驗本預測模型的精度，選取驗證序列對

xtest=(14，15 ，16，17，18，19，20)

ytest=（26.31，26.01，24.15，23.14，25.89，24.98，26.12）

將 xtest，w1，w2，…，w10，b 帶入下式：

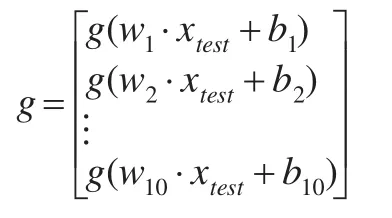
從而得到對成本預測數(shù)據(jù)的模擬值為：

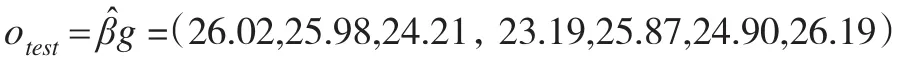
通過計算實際成本數(shù)據(jù)ytest與模擬成本數(shù)據(jù)otest的平均誤差為：

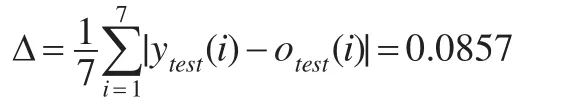
實際成本數(shù)據(jù)ytest與模擬成本數(shù)據(jù)otest的平均相對誤差為：

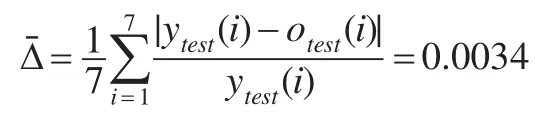
說明通過基于ELM方法訓練出來的企業(yè)成本預測模型的擬合精度較高，因此，該模型是可以作為該企業(yè)的成本預測模型的。

為了預測未來連續(xù)三個時期內的企業(yè)成本，選擇預測輸入向量為：

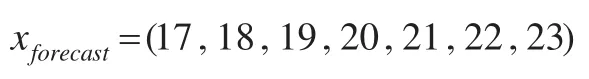
將 xforecast，w1，w2，…，w10，b帶入下式：

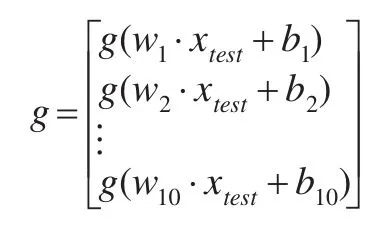
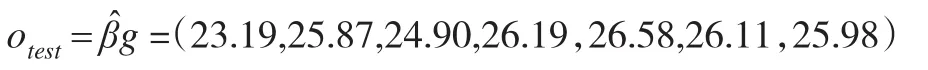
通過以上的基于ELM預測模型得到，未來三個時期內，該企業(yè)的成本預測結果為：

表3 某企業(yè)未來3個時期內的成本預測數(shù)據(jù) （單位：十萬元）

說明在第21個月內企業(yè)的會計成本將為26.58（十萬元），22個月的企業(yè)會計成本為26.11（十萬元）,第23個月的會計成本為25.98（十萬元）。即表明該企業(yè)的成本在未來的使用中將會呈現(xiàn)減少趨勢。

4 結語

成本預測從最初的定性預測方法為主到以數(shù)學模型為主的預測方法，考慮到成本預測過程中各影響因素的復雜性和多樣性，使得成本預測呈現(xiàn)多樣性和非線性，基于非線性的成本預測方法應該是未來成本預測的重心，本文對現(xiàn)有的非線性預測方法進行了分析，指出現(xiàn)有非線性預測方法的突出問題是模型復雜、計算量大，不利于成本預測模型的推廣和實際使用，而本文所提出的基于極限學習機原理的成本預測方法，其模型簡單，計算方便，易于掌握，且能反映出成本影響因素之間的非線性關系，因此，作為將ELM方法作為成本預測模型，能有效提升成本預測精度和使用范圍。

[1] 劉崇欣.基于模糊粗糙集的模具成本預測方法[J].計算機集成制造系統(tǒng),2012，(10).

[2] 訾書宇,魏汝祥,林名馳.成本預測系統(tǒng)中的自變量約簡方法[J].統(tǒng)計與決策,2012，(18).

[3] 李敬.基于TOPSIS的成本組合預測方法及其應用[J].統(tǒng)計與決策,2013，(4).

[4] Huang G B,Zhu Q Y,Siew C K.Extreme Learning Machine:Theory and Applications[J].Neurocomputing.2006,70(1).

[5] Huang G B,Chen L,Siew C K.Universal approximation using incre?mental constructive feedforward networks with random hidden modes[J].IEEE Transactions on Convexincrementalextremelearningmachine NeuralNetworks,2006,17(4).

[6] Huang G B,Chen L.Convexincre Mentalex Tremelearning Machine[J].Neurocomputing,2007,70(1).

[7] Huang G B,Li M B,Chen L,et al.Incremental Extreme Learning Ma?chine With Fully Complex Hidden Nodes[J].Neurocomputing.2008,71(4).

[8] uangG B,Li M B,Chen L,et al.Enhancedr and Omsearch Base Dvncremental Extre Melearning Machine[J].Neurocomputing,2008,71(4).