Finite elementmodeling of pavement responses based on stress-dependent properties of asphalt layer

Dong NiyaLi ChangNi Fujian，2

（1School of Transportation，Southeast University，Nanjing 210096，China）

（2Road Maintenance Technology Engineering Center of Jiangsu Province，Southeast University，Nanjing 210096，China）

Finite elementmodeling of pavement responses based on stress-dependent properties of asphalt layer

Dong Niya1Li Chang1Ni Fujian1，2

（1School of Transportation，Southeast University，Nanjing 210096，China）

（2Road Maintenance Technology Engineering Center of Jiangsu Province，Southeast University，Nanjing 210096，China）

In order to investigate the stress-dependent properties of hot-mix asphalt（HMA），a dynamicmodulus test was conducted on a group of AC-20 specimens at various stress states and loading frequencies，respectively．A userdefined material（UMAT）subroutine incorporating stressdependent constitutivemodelwas developed and finite element（FE）simulation was utilized to confirm the validity of the UMAT．A three-dimensional（3D）FE model for typical pavement structure was established，considering the HMA layer as a stress-dependentmaterial and other layers as linear elasticmaterials．Periodic load was applied to the pavement model and the pavement responses were calculated，including dynamicmodulus distributions，surface deflection，shear stress and tensile strain in the HMA layer，etc．Both test results and FE model predictions indicate that the dynamic modulus of asphalt concrete is sensitive to stress state and loading frequency．Using the nonlinear stress-dependentmodel results in greater predicted pavement responses compared with the linear elastic model．It is also found that the effects of stressdependency on pavement responsesbecomemore significantas loading frequency decreases．

dynamicmodulus test；loading frequency；stressdependentmodel；user-defined material（UMAT）subroutine；pavement responses

The property of stress-dependency is that the resilient modulus of a material can be affected by loading levels．For conventional design and mechanical analysis of the asphalt pavement structure，structural layers are usually simulated as linear elastic materials whose elastic moduli are constant at a certain temperature and remain unchangeable under different stress states．In fact，the pavement materials are not completely linear elastic．Nonlinear behaviors may appear as a result of complex traffic loading and environmental conditions．Asphalt layers are directly exposed to the environment and saddled w ith traffic loading，which results in complicated stress states，thus causing stress-dependent behavior．

To characterize stress-dependent properties，many constitutive equations have been proposed recently，and some of them have been w idely used in analyzing the stress-dependent behavior of pavementmaterials．In recent studies，A l-Qadi et al．［1］found using the stress-dependent modulus for the unbound base layer results in great predictions of pavement responses and little estimated pavement life for rutting and fatigue cracking．By performing a dynam ic modulus test，researchers found that the dynam ic modulus of asphalt concrete is susceptible to confining stress and loading frequency［2］．Collop et al．［3］found that the permanent vertical strains in the stress-dependent case are significantly greater than those in the non-stress-dependent case by using a stress-dependent constitutivemodel for asphalt．Antes et al．［4］used the results of the triaxial testing program to model the resilient modulus of asphaltm ixtures as a function of the applied stresses and found the effects of stress-dependency of asphaltm ixtures to be not negligible．Zhao et al．［5］developed a stress-dependentmodel for asphaltm ixtures based on the K-θmodel and investigated the influences of stress states on dynam ic modulus distribution w ithin the surface layer．Zeiada et al．［6］found that the confining pressure affects the dynamic modulus of asphalt concrete significantly，especially a_t low frequencies and high temperatures．Zhao et al．［79］further proposed amodelwhich employs the vertical shifting factor to characterize the pressure-dependent behavior of asphalt concrete，and the results show thatwhen the effect of confinement is considered，the dynamic modulus can be more than two times the uniaxial value at the same temperature and frequency．

So far，the stress-dependent behavior of asphalt concrete has not received extensive research．The study presented in this paper clarifies the effect of stress-dependent asphalt concretemodulus on pavement responses．

1 Dynam ic M odulus Test

In this study，basalt aggregates，filler and general 70＃bitumen are used to fabricate asphaltm ixture，the properties of which meet the requirements of guide of aggregate tests（JTGE20—2011）．The gradation of AC-20 listed in Tab．1 is designed in compliancew ith the Superpave volu-metric m ixture design procedure［10］．The volumetric design of the asphaltmixture results in a bitumen content of 4.4%by weight of the totalm ixture to meet a 4.0%target air void．

Tab.1 Gradation of AC-20 asphalt________m_ixture

First，asphaltm ixtures of 150 mm×170 mm（diameter ×height）were compacted using a Superpave gyratory compactor，and then each compacted sample was cored and sawn to produce cylindrical specimens w ith smooth and parallel ends and the prescribed dimension of 100 mm ×150 mm（diameter×height）for use in the dynam ic modulus test．The dynam ic modulus test was performed in a stress-controlled compressive mode by follow ing the general guidelines specified in Standard Method of Test for Determining Dynamic Modulus of Hot M ix Asphalt（AASHTO TP 62—2007）．The axial loading levelswere adjusted for each test condition to lim it the strain levels w ithin the range of 50 to 80×10－6and the total accumulated strain w ithin 1 500×10－6．

Dynamic moduliwere measured at the confining pressures of 35，138，and 207 kPa，the loading frequenciesof 0.1，0.5，1，5，10，and 25 Hz，and the temperature of 20℃．Three linear variable differential transformers（LVDT）weremounted onto the surface of the specimen．Three replicates were tested for each of the 18 combinations of confining pressure and loading frequency．Before the test，specimenswere conditioned at least2 h in an air bath in order to achieve the test temperature．Dynam ic modulusmeasurements are listed in Tab．2．Results show that dynam ic modulus increases as the loading frequency or confining stress increases，and the impact of loading frequency on dynam icmodulus is greater than that of confining stress．

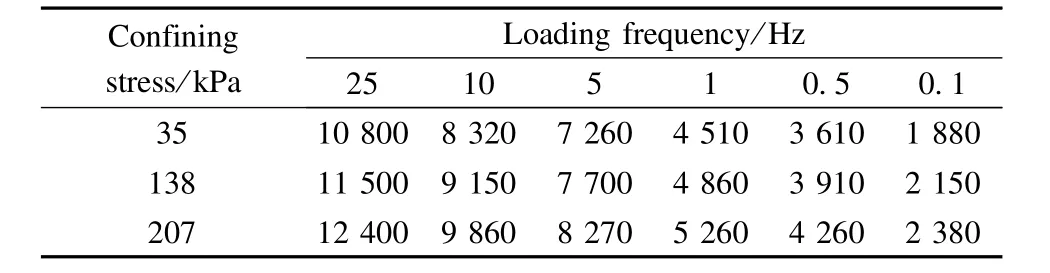
Tab.2 Results of dynam ic modulus E*at20℃___MPa

2 M odeling of Stress-Dependent Behavior

Themost commonly used stress-dependent constitutive model is the K-θmodel shown as

where E*is the dynamic modulus；θis the bulk stress，which is defined as the sum ofmaximum principal stress，intermediate principal stress and m inimum principal stress；K1，K2are the coefficients．The bulk stress is equivalent to the total value of axial stress and double confining stress．The solved model coefficients are listed in Tab．3．

In this UMAT subroutine，the stress-dependentmodulus was defined as Eq．（1）．The flow process of the subroutine w ritten in Fortran language is described as follows：1）The initial stress state and incremental strain from themain routine is obtained；2）The overburden and horizontal stresses are calculated；3）The total principal stress and direction are calculated；4）The bulk stress and resilientmoduli are calculated；5）The incremental Jacobianmatrices are calculated；6）The stress tensor is updated and returned to themain routine．

Since the stress-dependent modulus is varying，the nonlinear analysis is conducted by using an incremental loading and an iterative solution technique for each loading increment［1］．An incremental Jacobian matrix（also known as incremental-stiffnessmatrix）in the subroutine is defined as the ratio of incremental stress to incremental strain．Using the incremental strain tensor provided by the main routine，the UMAT subroutine is required to calculate the Jacobian matrix，update the total stress tensor for the current load increment，and then transmit the updated total stress tensor to themain routine．The Jacobian matrix ofmaterial constitutivemodel isw ritten as

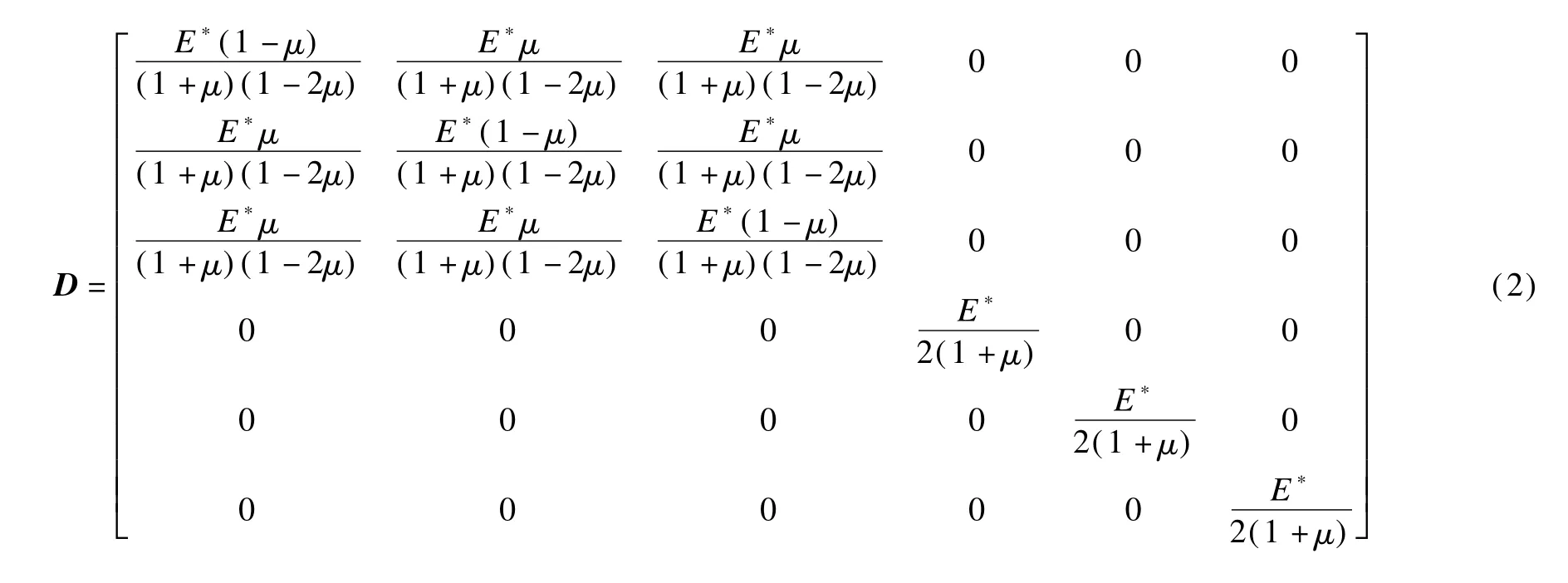
whereμis the Poisson’s ratio．

Tab.3 The values of K-θmodel coefficients for AC-20_

3 Verification of the UMAT Subroutine

As Fig．1 shows，a 3D FEmodel dimensionally sim ilar to the cylindrical specimen was developed by using ABAQUS Version 6.10 to confirm the validity of the UMAT subroutine．The periodic half-sine loads of different durations and amplitudeswere respectively applied on the top surface．The cylindricalmodel was partitioned into 5 488 20-node quadratic brick elements．

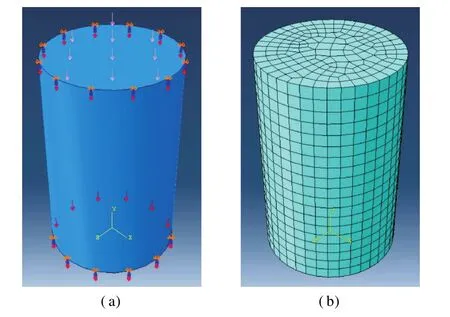
Fig.1 FEmodel of specimen．（a）Load application；（b）Model meshing

Tab．4 presents the absolute error and relative error between the test measured modulus and model predicted modulus at various loading frequencies．The maximum absolute error is 132 MPa，and the corresponding relative error，which is also themaximum，is less than 7%．Results show that good agreements are achieved between test measurements and model predictions，and the nonlinear approach taken in the UMAT subroutine is confirmed to be effective．

Tab.4 Comparisons betweenmeasured and predicted moduli

The structural type and mechanical properties of each layer are listed in Tab．5．The dimension of the pavement domain was3m×3 m×1.5m（length×w idth×depth）．The symmetrical boundary condition was considered in this pavementmodel and double rectangular loading areas were symmetrically distributed beside the centerline of the surface，as shown in Fig．2（a）．The traffic loading was modeled by a half-sine load of themaximum amplitude of 0.7 MPa applied on themodel surface．A 20-node quadratic brick elementwas used for the wholemodel，which was partitioned into 38 640 elements．Fine meshing was used around the loading areas，while relatively coarser meshing was used as the distance and depth to the load center increased，as shown in Fig．2（b）．

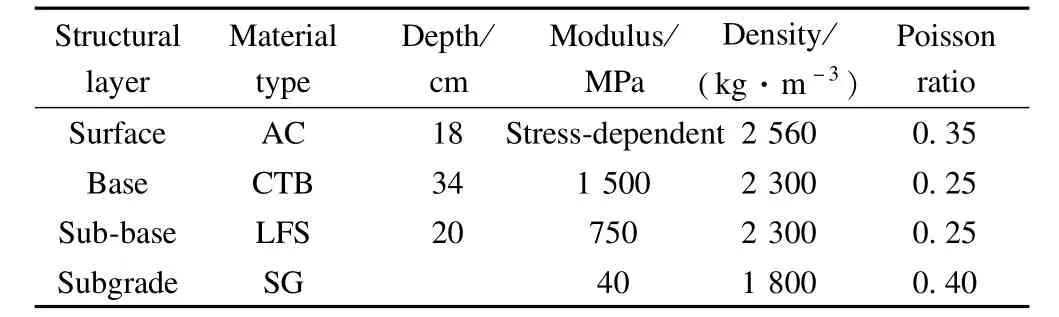
Tab.5 Structural type and mechanical properties of each layer

Fig.2 Pavement FE model．（a）Load application；（b）Model meshing．

4 Result and Analysis

The horizontal distributions of dynamic modulus at various transverse sections of the HMA layer at a loading frequency of 10 Hz and the vertical distributions at various loading frequencies are plotted in Figs．3（a）and（b），respectively．The maximum predicted modulus is observed at the surface of the HMA layer under the center of each loading area．The predicted modulus varies both horizontally and vertically due to the fact that the stress state alters throughout the HMA layer．It is evident that the predicted modulus decreases sharply as the horizontal distance to the load center increases．In most cases，thepredicted modulus w ithin the loading area decreases as vertical depth increases，w ith the exception of the area around the wheel gap center．The trends of predicted modulus observed in Fig．3（b）are reasonable and in accordance w ith expectations．The predicted modulus under the load center decreases as the vertical depth increases．The reduction of the predicted modulus becomesmore significantwhen the pavement is loaded at a high frequency．

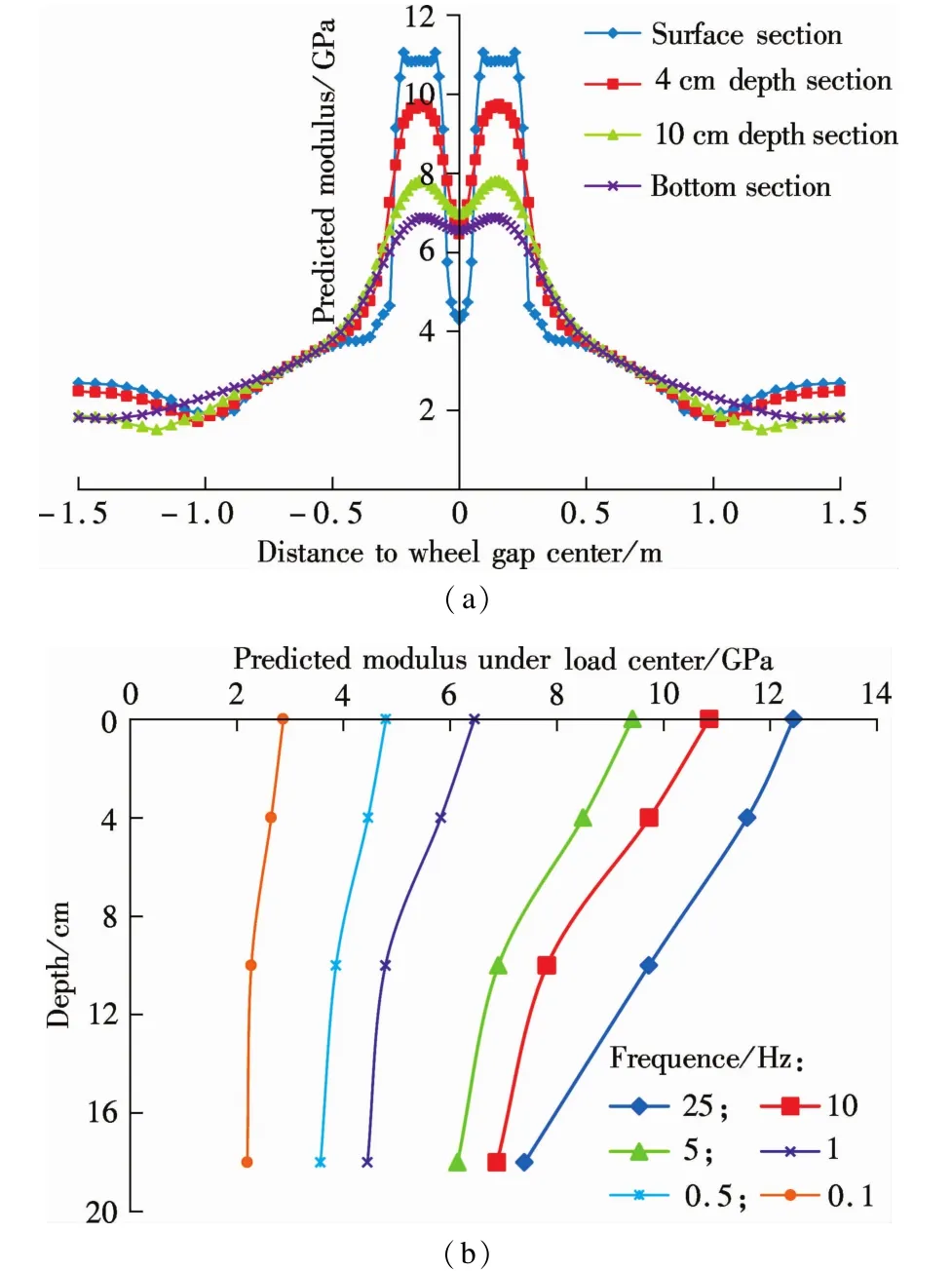
Fig.3 Distributions of the predicted modulus．（a）Horizontal distributions at various sections at 10 Hz；（b）Vertical distributions at different loading frequencies

As shown in Fig．4，the maximum deflection is observed under the center of each loading area，and surface deflection increases as the loading frequency decreases．However，there are no obvious differences in the deflection basin curve w ithin a range of loading frequencies（1 to 10 Hz）．In contrast，the augment of themaximum deflection is significantwhen the loading frequency varies from 25 to 10 Hz or 0.5 to 0.1 Hz．The results demonstrate that surface deflection is sensitive to the loading frequency，especially above 10 Hz or below 0.5 Hz．

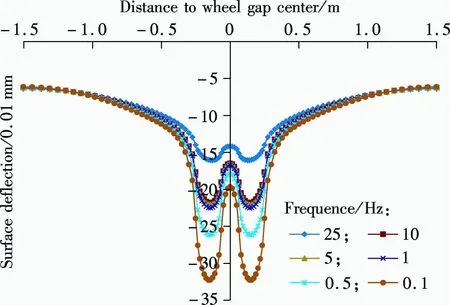
Fig.4 Surface deflection basins at different loading frequencies

In this study，the shear stress specifically represents the maximum shear stress，which value is equivalent to the difference between the maximum principal stress and the m inimum principal stress．As shown in Fig．5（a），when the pavement is loaded at 25 Hz，the shear stress close to the surface is positive ow ing to the fact that the m inimum principal stress is greater than the maximum principal stress；as depth increases，the shear stress gradually turns to negative and shares a sim ilar development w ith other loading conditions．Apart from this exception，the shear stress increases in the upper portion of the surface layer，then decreases in the lower part．The shear stress increases as the loading frequency decreases．The maximum shear stresses at each loading frequency are all observed at7 cm depth of the HMA layer．W ith the loading frequency varying from 25 to 0.1 Hz，the maximum shear stress increases by 20%．

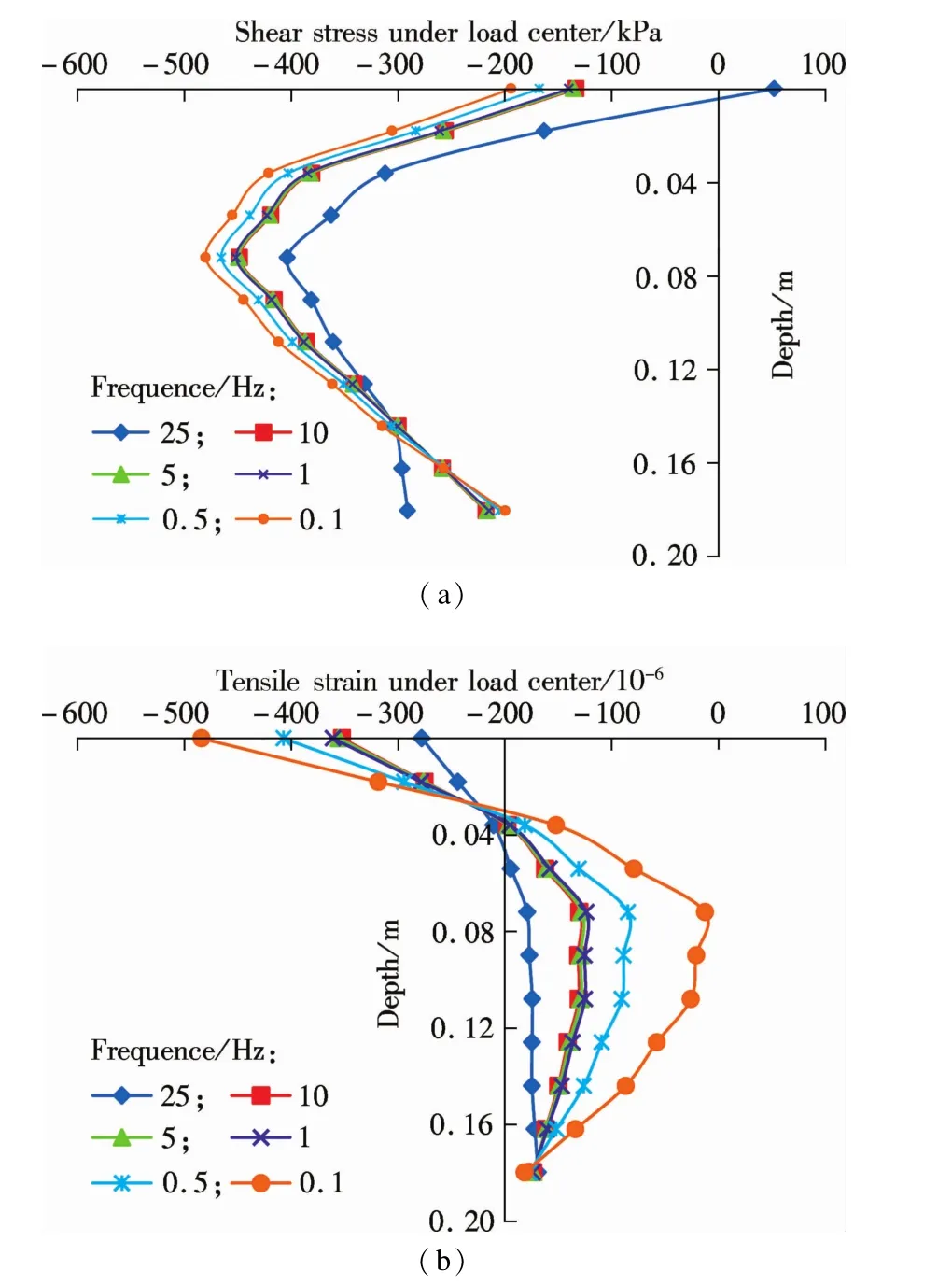
Fig.5 Vertical distributions．（a）Shear stresses；（b）Tensile strains at various loading frequencies

Fig．5（b）illustrates the vertical distributions of tensile strains w ithin the HMA layer at various loading frequencies．The change in tensile strain consists of three stages．At beginning，the tensile strain gradually increases from negative to zero．Then，it constantly increasesfrom zero to the maximum．Finally，it decreases as the vertical depth increases．However，the third stage at 25 Hz is inconspicuous，and it remains fundamentally unchanged．It is clear that the lower the loading frequency，the greater the tensile strain（absolute value）．Themaximum tensile strain increases 8.3 timeswhen the loading frequency varies from 25 to 0.1 Hz，but the differences in the tensile strain are small at loading frequencies of 1 to 10 Hz．From the above，the impact of the loading frequency on tensile strain w ithin the HMA layer is remarkable，especially at low loading frequencies．

Tab．6 summarizes the predicted pavement responses at selected positions based on the linear elastic and nonlinear stress-dependent models at various loading frequencies．It is apparent that all types of model predictions listed in the table become greater as the loading frequency decreases．The use of the nonlinear stress-dependentmodel for the HMA layer leads to greater predicted pavement responses in comparison w ith the linear elastic model．It is found that the maximum pavement responses are all achieved from the stress-dependent model at0.1 Hz，indicating that the effects of stress-dependency in asphalt concrete and frequency of traffic loading are significant for pavement responses．

Tab.6 Comparisons of predicted pavement responses between linear and nonlinearmodels

5 Conclusion

Based on the predicted pavement responses obtained from different constitutive models，conclusions can be drawn as follows：

1）Using the nonlinear stress-dependentmodel results in greater predicted pavement responses than using the linear elastic model，including surface deflection，shear stress and tensile strain in the HMA layer，tensile stresses at the bottom of the base and sub-base，and compressive strain at the top of the subgrade．

2）Predicted pavement responses increase as the loading frequency decreases．However，it is found that sensitivity to loading frequencies of 1 to 10 Hz is less compared to other loading frequencies．

3）The effects of stress-dependency on surface deflection and tensile strain in the HMA layer becomemore significant as the loading frequency decreases．

［1］A l-Qadi I，Wang H，Tutum luer E．Dynam ic analysis of thin asphalt pavements by using cross-anisotropic stressdependent properties for granular layer［J］．Transportation Research Record，2010，2154：156- 163．

［2］Ma X，Ni F J，Chen R S．Dynam ic modulus test of asphaltm ixture and predictionmodel［J］．China Journalof Highway and Transport，2008，21（3）：35- 39．（in Chinese）

［3］Collop A C，Scarpas A，Kasbergen C，et al．Development and finite element implementation of stress-dependent elastoviscoplastic constitutive model w ith damage for asphalt［J］．Transportation Research Record，2003，1832：96- 104．

［4］Antes PW，Van Dommelen A E，Houben JM，et al．Stress-dependentbehavior of asphaltm ixtures athigh temperatures［C］／／Proceedings of the Technical Sessions．Lexington，USA：Association of Asphalt Paving Technologist，2003，72：173- 195．

［5］Zhao Y Q，Tan Y Q，Yu X．Stress-dependentmechanical behavior of asphalt m ixtures［J］．Journal of Huazhong University of Science and Technology：Natural Science Edition，2010，38（10）：124- 127．（in Chinese）

［6］Zeiada W，Kaloush K，Biligiri K，et al．Significance of confined dynamic modulus laboratory testing for asphalt concrete：conventional，gap-graded，and open-graded m ixtures［J］．Transportation Research Record，2011，2210：9- 19．

［7］Zhao Y Q，Tang J，Liu L．Construction of triaxial dynam ic modulus master curve for asphalt mixtures［J］．Construction and Building Materials，2012，37（12）：21 -26．

［8］Zhao Y Q，Liu H，Liu W．Characterization of linear viscoelastic properties of asphalt concrete subjected to confining pressure［J］．Mechanics of Time-DependentMateri-als，2013，17（3）：449- 463．

［9］Zhao Y Q，Bai L，Liu H．Implementation of a triaxial dynam icmodulusmaster curve in finite-elementmodeling of asphalt pavements［J］．Journal of Materials in Civil Engineering，2014，26（3）：491- 498．

［10］AASHTO R 35-04．Standard practice for Superpave volumetric design for hotm ix asphalt（HMA）［R］．Washington DC：American Association of State Highway and Transportation Officials，2004．

基于瀝青面層應力依賴性的路面響應有限元模擬

董尼婭1李 昶1倪富健1，2

（1東南大學交通學院，南京210096）
（2東南大學江蘇省道路養護工程技術研究中心，南京210096）

為了探究瀝青混合料的應力依賴性質，分別在不同應力狀態及荷載頻率下對一組AC-20試件進行了動態模量試驗．開發了一個包含應力依賴本構模型的用戶自定義材料子程序并利用有限元模擬證實了其有效性．建立了一個典型路面結構的三維有限元模型，將瀝青面層視為應力依賴性材料，而其他結構層為線彈性材料．對路面模型施加周期性荷載，并計算得到路面響應，包括動態模量的分布、路表彎沉、瀝青面層的剪應力及拉應變等．試驗結果及有限元模型預測值均表明了瀝青混凝土的動態模量對應力狀態及荷載頻率具有敏感性．與線彈性模型相比，使用非線性應力依賴模型得到的預測路面響應更大；應力依賴性對路面響應的影響隨著荷載頻率的減小變得更加顯著．

動態模量試驗；荷載頻率；應力依賴性模型；UMAT子程序；路面響應

U416.217

10．3969／j．issn．1003－7985．2015．03．018

2014-12-28．

Biographies：Dong Niya（1987—），female，graduate；Ni Fujian（corresponding author），male，doctor，professor，nifujian＠gmail．com．

Jiangsu Provincial Transportation Science and Technology Project（No．2011Y02-1-G1）．

：Dong Niya，Li Chang，Ni Fujian．Finite elementmodeling of pavement responses based on stress-dependent properties of asphalt layer［J］．Journal of Southeast University（English Edition），2015，31（3）：401- 406．

10．3969／j．issn．1003－7985．2015．03．018