靜電場中的常見圖象及應用

曾明

靜電場既是高中物理的重點，又是難點，它所涉及的物理量較多，關系復雜.由于在討論各個物理量之間的關系時，很多學生都習慣用函數關系式，有些問題就顯得特別復雜.其實，如果能用圖象處理有些靜電場中的問題，往往可以達到化難為易，化繁為簡的目的.同時應用圖象研究物理問題，還有利于培養學生數形結合，形象思維，靈活處理物理問題的能力，也是高考中體現能力的命題點.

下面就舉例分析靜電場中常見圖象問題的處理方法.

一、靜電場中的E-x圖象

圖象表示電場中的場強隨坐標變化的函數關系，圖象與x軸圍成的面積表示電勢差.

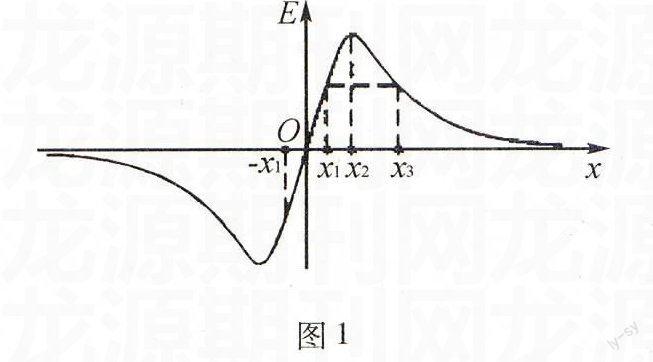
例1空間有一沿x軸對稱分布的電場，其電場強度E隨x變化的圖象如圖1所示.下列說法正確的是（ ）.

A.O點的電勢最低

B.x2點的電勢最高

C.x1和-x1兩點的電勢相等

D.x1和x3兩點的電勢相等

解析電場強度是矢量，正負表示方向.由圖象可知，從坐標原點沿x軸正方向，場強方向與+x方向相同，從坐標原點沿x軸負方向，場強與-x方向相同.因為沿著電場線的方向電勢降低，所以從坐標原點O沿x軸正方向電勢降低，從坐標原點沿x軸負方向電勢也降低，故坐標原點O的電勢最高，A、B錯誤.由于電場沿x軸對稱分布，從圖象可以看出，從坐標原點O沿+x方向和-x方向經相同距離x1，E-x圖象和x軸所圍成的面積相等，即電勢降低相同的量，所以C正確.從x1到x3是沿著電場線的方向，所以x3點的電勢比x1點的電勢低，D錯誤.本題正確答案是C.

點評解答本題的關鍵是：（1）知道在一維坐標中，矢量的方向用正負表示；（2）沿著電場線的方向電勢越來越低；（3）E-x圖象和x軸所圍成的面積表示電勢差.

二、靜電場中的φ-x圖象

圖象表示電勢隨坐標變化的函數關系，圖象上某點切線的斜率表示該位置的電場強度.

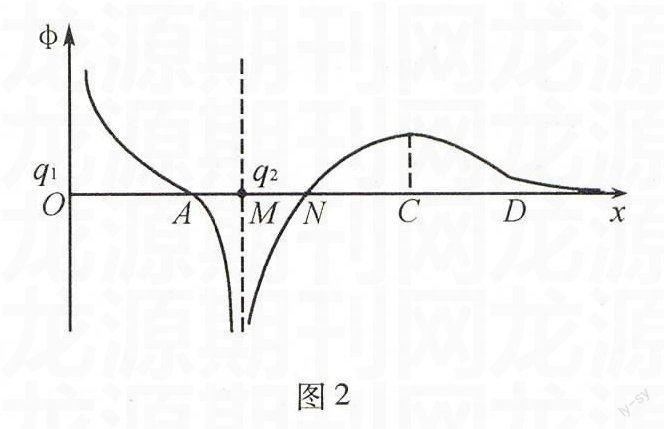
例2兩電荷量分別為q1和q2的點電荷放在x軸上的O、M兩點，兩電荷連線上各點電勢φ隨x變化的關系如圖2所示，其中A、N兩點的電勢為零，ND段中C點電勢最高，則（ ）.

A.C點的電場強度大小為零

B.A點的電場強度大小為零

C.NC間場強方向向x軸正方向

D.將一負點電荷從N點移到D點，電場力先做負功后做正功

解析由于φ-x圖象某點切線的斜率表示該點電場強度的大小，所以C點的場強大小為零，而A點的場強大小不為零，A正確，B錯誤；從圖象上的N點到C點，電勢不斷增大，根據沿著電場線電勢降低可知，電場強度方向應向x軸的負方向，C錯誤；從N到D，電勢先增大后減小，故負電荷的電勢能先減小后增大，因而電場力先做正功后做負功，D錯誤.本題正確答案為A.

點評正確解答本題的關鍵是：

（1）知道φ-x圖象的切線斜率表示電場強度的大小；

（2）沿著電場線的方向電勢降低；

（3）正電荷在電勢高處電勢能大，負電荷在電勢高處電勢能小；（4）電場力做正功，電勢能減小，電場力做負功，電勢能增加.

三、靜電場中的v-t圖象

圖象表示電荷運動速度隨時間變化的關系，圖象上某點切線的斜率表示加速度，圖象與t軸圍成的面積表示位移.

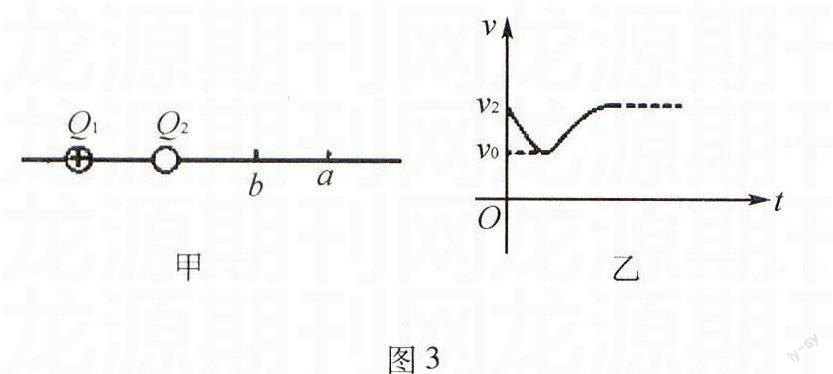
例3如圖3甲所示，Q1、Q2為兩個固定點電荷，其中Q1帶正電，它們連線的延長線上有a、b兩點.一正試探電荷以一定的初速度沿直線從b點開始經a點向遠處運動，其速度圖象如圖3乙所示.則（ ）.

A.Q2帶正電B.Q2帶負電

C.試探電荷從b到a的過程中電勢能增大

D.試探電荷從b到a的過程中電勢能減小

解析試探電荷從b點開始經a點向遠處運動時，處在Q1和Q2電荷產生的合電場中.由圖3乙可知，試探電荷先做減速運動，若Q2為正，則該電荷將一直加速，故Q2為負，A錯誤，B正確；試探電荷從b到a的過程中，由圖3乙可知，電荷做減速運動，故電場力做負功，因此電勢能增大，故C正確，D錯誤，本題正確答案是BC.

點評解答本題的關鍵是：（1）電場的疊加：（2）物體做加、減速運動的條件；（3）電場力做功和電勢能變化的關系.

四、靜電場中的E-t圖象

圖象表示電場中的場強隨時間變化的關系.

例4一電荷量為q（q>0）、質量為m的帶電粒子在勻強電場的作用下，在t=0時由靜止開始運動，場強隨時間變化的規律如圖5所示.不計重力，求在t=0到t=T的時間間隔內

（1）粒子位移的大小和方向；

（2）粒子沿初始電場反方向運動的時間.

解析（1）粒子在0～T/4、T/4

～T/2、T/2～3T/4、3T/4～T時間間隔內做勻變速運動，

設加速度分別為a1、a2、a3、a4，由牛頓第二定律得qE0=ma1、2qE0=-ma2、2qE0=ma3、qE0=-ma4.

由此得帶電粒子在0～T時間間隔內運動的a-t圖象如圖6（a）所示，對應的v-t圖象如圖（b）所示，其中

v1=a1T4=qE0T4m

由圖6（b）可知，帶電粒子在t=0到t=T時的位移為

s=T4v1，

聯立解得s=qE0T216m

它的方向沿初始電場正方向.

（2）由圖（b）可知，粒子在t=3T/8到t=5T/8內沿初始電場反方向運動，總的運動時間為t=5T8-3T8=T4.

點評解答本題要注意：（1）研究帶電粒子在交變電場中運動，一定要分段進行；（2）通過圖象轉換直觀地表示出帶電粒子的運動情況；（3）知道加速度圖象與t軸所圍成的面積表示速度改變的大小，正負表示方向，速度圖象與t軸所圍成的面積表示位移大小，正負表示方向.

五、靜電場中的φ-t圖象

圖象表示電場中的電勢隨時間變化的關系.

例5如圖7所示，A、B為一對中間開有小孔的平行金屬板，相距一定距離，A板接地，現有一電子在t=0時刻在A板小孔中由靜止開始向B板運動，不計重力及阻力影響，使電子一定能從B板小孔射出，則B板電勢φB與時間t的變化規律是圖8中的（ ）.

解析答案A，加在B板上的電勢總為正，且大小恒定不變，那么電子進入電場之后，將一直受到向上的電場力的作用，所以電子一直做加速運動，一定能從B板小孔飛出，所以A正確.

答案B，B板上的電勢按照正弦規律變化，電子進入電場之后，先是向上做加速運動，且加速度先增大后減小，當B板上電勢變為負值的時候，電子做向上的減速運動，根據對稱性可知，當電勢再次減為零的時候，即4s時，電子的速度恰好也減為零，之后，電場又變為正，重復上面的過程，整個過程中，電子一直向上運動，可以從B點飛出， B正確.

答案C，B板上的電勢按照余弦規律變化，電子進入電場之后，先是向上的加速運動，當電勢變為負值的時候，電子做向上的減速運動，直到速度減為零，之后，由于電勢還是負值，所以電子要做反向的加速運動，根據對稱性可知，當電勢變為零的時候，電子的速度最大，之后又開始做減速運動，當速度減小為零的時候，電勢最大，之后再重復前面的過程，所以電子做的是上下的往復運動，不一定能夠從小孔射出，所以C錯誤.

答案D，電子的運動情況和答案C類似，只不過在各段時間內電子都做的是勻加速和勻減速直線運動，運動的情況和答案C類似，也是往復運動，不一定能夠從B板上的小孔射出，所以D錯誤.正確答案是AB.

點評解答本題的關鍵是：（1）分段處理；（2）正確分析各個過程中的受力和運動情況；（3）特別注意對稱性.

六、靜電場中的Ep-x圖象

圖象表示電荷的電勢能隨坐標值變化的函數關系，圖象上某點切線的斜率代表電場力.

例6一帶負電的粒子只在電場力作用下沿x軸正向運動，其電勢能Ep隨位置x變化的關系如圖9所示，其中0～x2段是關于直線x=x1對稱的曲線，x2～x3段是直線，則下列說法正確的是（ ）.

A.x1處電場強度最小，但不為零.

B.粒子在0～x2段做勻變速運動，x2～x3段做勻速直線運動

C.在0、x1、x2、x3處的電勢φ0、φ1， φ2， φ3的關系為φ3>φ2=φ0>φ1.

D.x2～x3段的電場強度大小方向均不變，為一定值.

解析在x1處，圖象切線的斜率為零，故電荷在該點的電場力為零，即場強為零.答案A錯誤.

在0～x2的過程中，圖象的切線斜率先減小后增大，電場力先減小后增大，故不是勻變速運動.而x2～x3段的斜率不變，電場力不變，電場強度大小和方向也不變，做勻變速運動，故B錯誤，D正確.

在0、x1、x2、x3處，電勢能的關系為：Ep3>Ep2=Ep0>Ep1，由于粒子帶負電，故電勢關系為：φ3<φ2=φ0<φ1，故C錯誤.

本題正確答案是：D

點評解答本題的關鍵是：（1）Ep-x圖象的斜率代表電場力；（2）負電荷在高電勢處的電勢能小.

七、靜電場中的C-d圖象

圖象表示電容器的電容與極板之間距離變化的關系.

例7如圖10所示為一只“極距變化型電容式傳感器”的部分構件示意圖.當動極板和定極板之間的距離d變化時，電容C便發 生變化，通過測量電容C的變化就可知道兩極板之間距離d的變化情況.在下列圖中能正確反映C與d之間變化規律的圖象是 （ ）.

解析動極板和定極板組成了一個平行板電容器，其電容C=εs4πkd，由于ε和S保持不變，C和d成反比，故C-d圖象是一條雙曲線.正確答案是A.

點評解答本題的關鍵是：（1）知道動極板和定極板構成一個平行板電容器；（2）寫出自變量d和函數C的函數關系式.

（收稿日期：2015-02-09）