礦山臺階爆破震動速度預測方法的研究

李小武，周　銘，胡　韜，代雨昊，何皇兵（昆明有色冶金設計研究院股份公司，云南　昆明　650051）

礦山臺階爆破震動速度預測方法的研究

李小武，周銘，胡韜，代雨昊，何皇兵
（昆明有色冶金設計研究院股份公司，云南昆明650051）

摘要：針對某露天礦山采場附近居民房屋出現裂縫的問題，進行礦山居民房屋現場測震，并現場實驗檢驗了傳統薩道夫斯基線性回歸方法與BP神經網絡預測震動速度的兩種方法的可靠性，采用BP神經網絡方法進行爆破震動質點速度的預測，再通過調整爆破設計降低爆破震動，保障了房屋的安全。

關鍵詞：礦山爆破；爆破震動；神經網絡預測；房屋安全

0　引　言

爆破技術在采礦、鐵路及國防建設等方面有著廣泛地應用，爆破工作不可避免的會產生一些負面效應，如爆破震動、沖擊波、飛石、噪聲等，而爆破震動是爆破施工作業中最嚴重的負面效應。

減小爆破施工負面效應的最重要方法就是預測爆破震動。實測結果表明：爆破震動強度與炸藥量、爆心距、巖土性質以及場地條件等因素密切相關。國內外采用預測爆破震動速度的公式不盡相同，見表1［1］。

表1　世界各國對爆破震動質點振速峰值預測公式Tab.1　Worldwide prediction formula of the vibration velocity peak of blasting vibration particles

人工神經網絡的出現，國內外許多學者采用神經網絡對爆破震動速度進行預測，在眾多神經網絡的算法中，BP人工神經網絡在爆破震動峰值振速預測中應用最多，Mohamed、Amnieh、徐全軍、沈蔚等采用BP人工神經網絡進行爆破震動峰值預報［3－8］。

1　工程背景

某礦山在開采過程中，與采場周邊的村民發生了比較突出的矛盾之一是采場臺階爆破作業對周邊的民用建筑房屋的震動損害與破壞，造成企業與村民關系緊張，給礦山的建設與生產帶來了一定的影響。

根據采場目前爆破設計的情況，計算得到的爆破震動最大影響距離為113 m，爆破飛石影響為115 m，而爆破確定的安全界線是爆破作業區200 m以外，因此從爆破震動的計算影響范圍來講爆破作業對房屋應該是沒有影響的。針對村民多次反映的房屋墻面裂縫等問題，見圖1。礦山進行調查后認為主要的原因是：采礦場周圍的自建房屋結構簡單、房齡偏長和存在隱性的裂縫，抗震等級難以保證；同時，采場爆破加劇了房屋的損壞。為了緩和企業與居民的關系，不至于影響礦山生產，在不考慮對房屋進行搬遷的情況下，尋求降震的方法。

圖1　房屋裂縫情況Fig.1　Cracks of house

2　降震技術措施

震動速度的影響因素也就是降震技術中需要處理的因素。根據國內外許多爆破工作者及科研工作者的研究與總結，降震技術措施大致有以下幾種方法：

1）爆源控制降震

（1）減小單段最大起爆藥量

由薩氏公式分析，可知單段最大起爆藥量Q 是3個影響質點速度V的因素中可以進行調控的因素，單段最大起爆藥量越大，質點震動速度越大。在礦山實際生產中，可以進行孔內微差起爆的方法，來減小單段最大起爆藥量。大量試驗研究表明，產生地震效應跟爆破炮孔之間的微差時間有著密切的關系。微差時間的確定有3個原則：①使排間延發時間大于排內延發時間；②選取微差時間應使前后起爆的炸藥量產生的地震波互相干擾；③使前后起爆的炸藥量產生的地震波主震相不重疊。研究表明，微差時間一般選取30～50 ms為宜。需要根據不同的爆破場地的地質條件和環境，通過試驗和長期觀察來確定，這種方案爆破技術人員在現場比較容易控制與調整。

[7]列寧：《列寧專題文集·論辯證唯物主義和歷史唯物主義》，北京：人民出版社，2009年，第161頁。

（2）合理的孔網參數

國內外露天礦山臺階爆破孔網參數多采用“大孔距”爆破參數，大量試驗研究表明，在保持每個炮孔負擔面積基本不變的情況下，適當地減小排距而加大孔距，不僅可以使爆破效果得到改善，而且能減少爆破地震波效應。工程技術人員長期在現場負責，了解實際地質情況，才能更好地調整好孔網參數。

（3）擁有良好的自由面

爆破試驗研究得知，爆破時越靠近自由面的炮孔，產生的爆破震動越小，因此，爆破作業中的每個炮孔必須有自由空間以配合微差技術，從而使后排炮孔爆破產生的壓縮波從這些自由面中反射，從而降低爆破震動。隨著雷管精度的不斷提高，逐孔起爆技術廣泛地應用于礦山臺階爆破，為臺階爆破提供了良好的自由面。

（4）選擇合適的爆破作用指數

對露天各種大的爆破工程，爆破作用指數的大小很大程度上影響著爆破震動的強度，在一定的范圍內成反比關系。因此礦山臺階爆破中應盡可能獲得最大松動的爆破條件，以減少爆破震動強度。但該礦山由于生產情況，采用強制的壓碴拋擲爆破。

2）截斷傳播路徑進行隔震

采用減震溝減震可以干擾和阻隔爆破地震波的傳播，減震溝對爆破地震波起到反射和繞射，降低了爆破地震波的強度，從而加快了爆破地震波的衰減，達到了控制爆破震動的作用。但該方法操作起來復雜，礦山技術上的力量也不足，因此不予采納。

3　質點震動速度預測

對爆破震動進行預測是采取有效爆破方案的前提。單段最大起爆藥量是控制爆破震動影響的關鍵。在幾所居民民房里安裝測震儀進行測震，包括爆心距、單段最大起爆藥量、臺階爆破處與測震點高程、爆心距方向線與自由面的夾角和測點處質點震動速度，見圖2，共收集了16組數據，見表2。根據建筑物安全允許的震動速度，見表3，民房建筑物的允許震動速度為2.0 cm／s，可知其震動并未超過安全允許值，但由于房屋老化，參照相關經驗適當地降低其安全允許值為1.5 cm／s，再設計爆破方案，以達到降低爆破震動的原因。采用傳統的薩氏公式進行線性回歸與智能BP神經網絡進行爆破震動的預測。

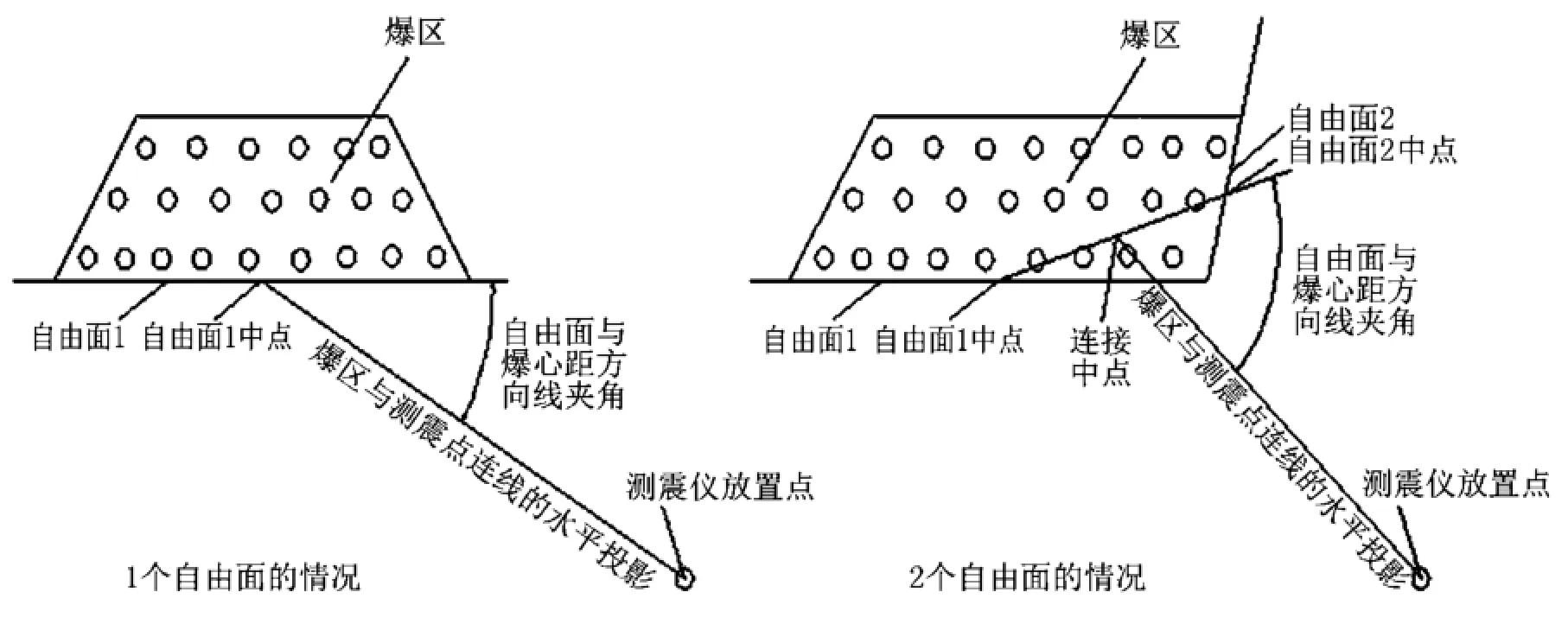
圖　2　爆心距與自由面的夾角Fig.2　Angle between blasting center distance and free surface

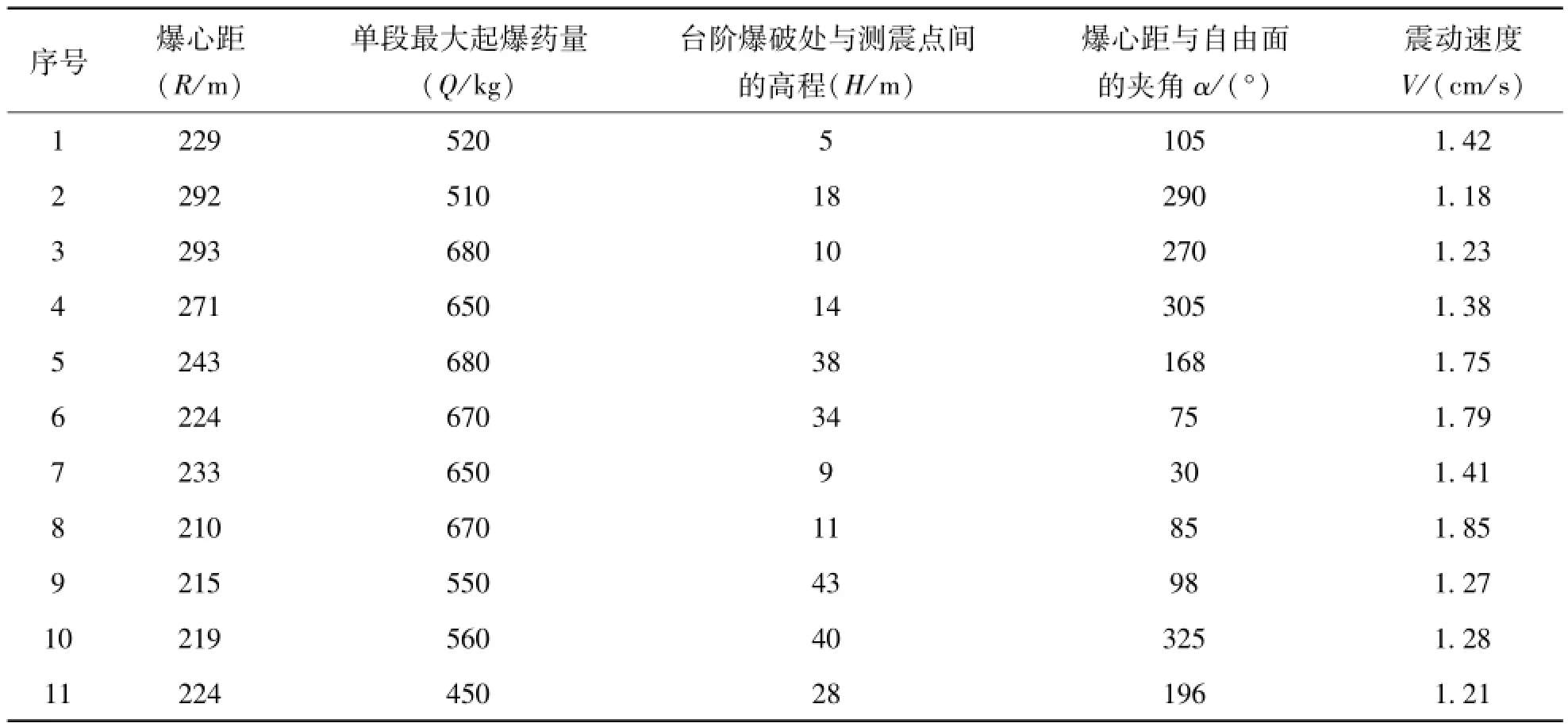
表2　爆破試驗震動速度Tab.2　Blasting vibration velocity

序號　爆心距（R／m）單段最大起爆藥量（Q／kg）臺階爆破處與測震點間的高程（H／m）爆心距與自由面的夾角　α／（°）震動速度V／（cm／s）12　286　580　16　335　1.11 13　295　600　14　231　1.09 14　278　500　7　256　1.05 15　204　680　24　67　1.95 16　289　640　25　117　1.31

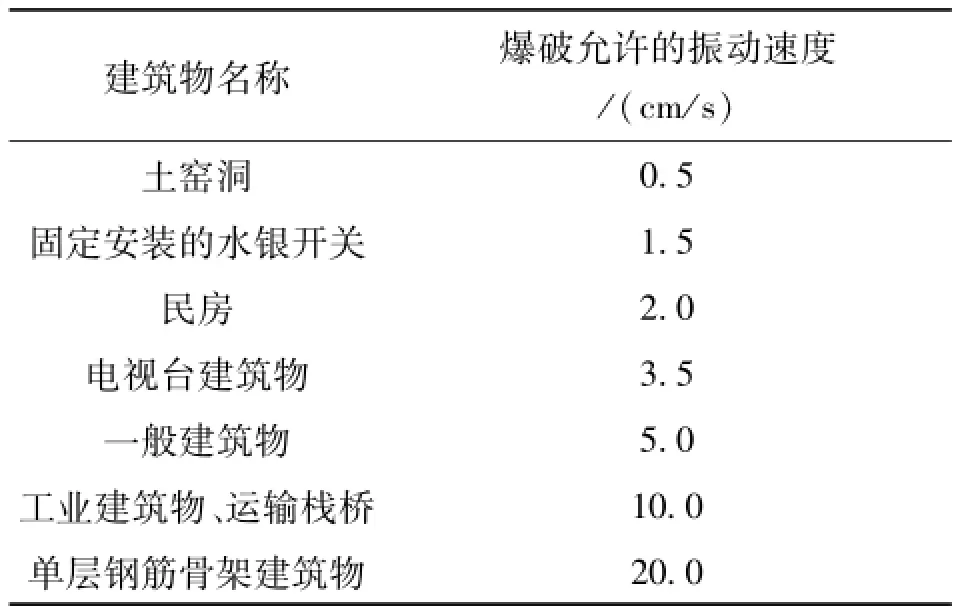
表3　國內建筑物允許震動速度Tab.3　Domestically permitted building vibration velocity

3.1線性回歸預測分析

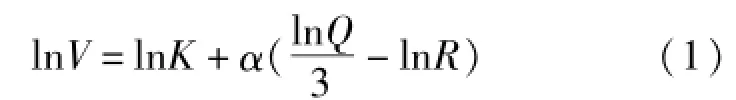
已編入《爆破安全規程》的薩道夫斯基公式是國內計算爆破震動的依據，對薩氏公式等號兩端取對數，得到：由于在同一地區，K與α都是常數可知，令y＝ lnV，x＝lnQ－lnR，b＝lnK，（1）式簡化為y＝b＋ ax，即lnV與－lnR具有線性關系。由線性回歸計算得到K＝57.2797，α＝1.1037。代入薩氏公式得到：

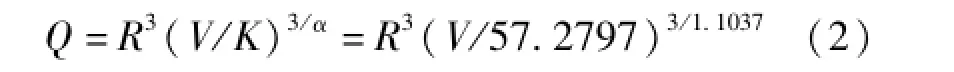
由表3的允許安全震動速度V＝1.5 cm／s和房屋離最近的爆破點的距離為204 m，代入公式（2）中得到單段最大起爆藥量為425.65 kg。

將K與α的值代入薩氏公式中得到預測爆破震動公式：

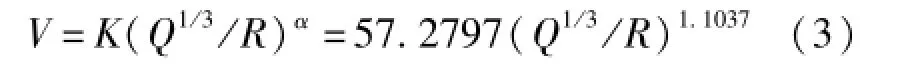
將公式（3）計算得到的線性回歸震速值與實際測量值進行誤差分析，以檢驗公式的準確性，如表4所示。誤差大多數均在10%以內，只有第5、6、9、10及11次超過10%。近年來不少學者對誤差大的原因進行研究表明：這是由于測震點與爆破處的高程所引起的［9］。

表4　線性回歸震速計算值與實際測量值誤差分析Tab.4　Error analysis on the calculated vibration velocity by linear regression and the actual measured value

3.2神經網絡預測分析

BP人工神經網絡是采用反向傳播算法的一種神經網絡，它是一種監督訓練多層網絡的算法，主要原理是通過學習，使網絡的輸出層的誤差平方和達到最小。以爆破震動主要影響的4個因素：單段最大起爆藥量Q、爆心距R、測震點與臺階爆破處的高程H以及爆心距與自由面的夾角α為作為神經網絡輸入；采用3層BP神經網絡，以爆破震動速度V作為神經網絡的輸出。構成1個多個輸入單個輸出的神經網絡，隱含層神經元個數采用6個，其拓撲結構見圖3（圖中左側為輸入元素，右側為輸出元素）。網絡訓練數據采用表2中的16組數據，神經網絡訓練采用的是trainlm函數，誤差傳遞采用的是tansig函數，誤差采用的是mse函數，訓練步驟設置為4 000步，迭代訓練精度達到0.001。用訓練好的網絡就可以進行爆破震動速度的預測。

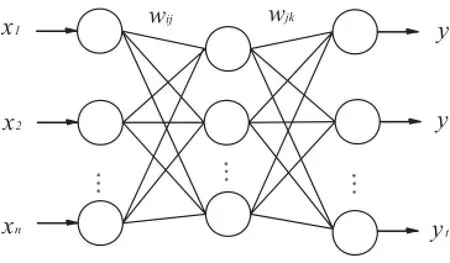
圖3　神經網絡拓撲結構Fig.3　Topology of neural network

4　現場檢驗

隨機進行了9次爆破測震試驗用于檢驗2種爆破震動預測方案的可靠性，試驗數據見表5。表中V測1由公式（4）計算得到，V測2由BP神經網絡得到，V實由測震儀實際測量得到。從表5中可以看出線性回歸的最大相對誤差為20%，不超過10%的次數為6次，而神經網絡的最大相對誤差為15.38%，不超過10%的次數為7次。神經網絡預測值與實測值的對比及絕對誤差的對比分別見圖4、圖5。從圖4中可以看出神經網絡預測值貼近與實際測量值附近，圖5可以神經網絡預測值的絕對誤差曲線更接近X軸，因此相比較而言，實驗說明了神經網絡在預測爆破震動強度時更準確一些。

表5　爆破質點震動速度誤差對比Tab.5　Error comparison of vibration velocities of blasting particles

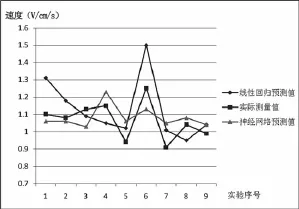
圖4　預測值與實測值的對比Fig.4　Comparison between predicted and measured values

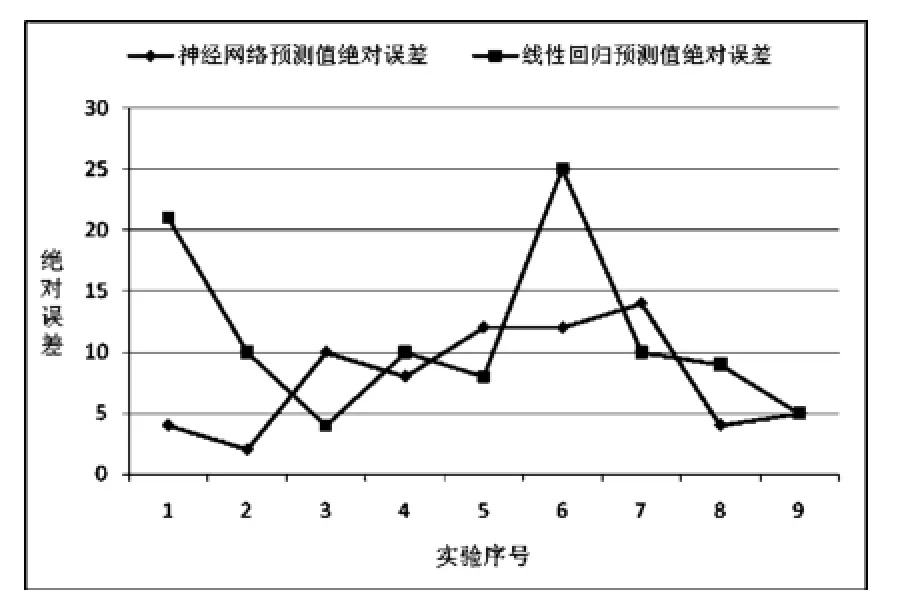
圖5　預測值與實測值絕對誤差的對比Fig.5　Absolute error comparison between predicted and measured values

5　結　語

對設計方案進行爆破質點的震動速度的神經網絡方法預測后以調整單段最大起爆藥量，并采用孔間微差起爆技術，在房屋進行修補之后再未出現裂縫情況。

1）薩氏公式線性回歸分析與BP神經網絡均可以用于爆破質點速度的預測，但神經網絡考慮對爆破震動強度的影響因素比薩氏公式更多，采用BP人工神經網絡方法預測的爆破震動峰值振速更接近實測值，表明了BP人工神經網絡方法預測爆破震動強度的優越性。

2）采用在設計中提前預測爆破質點的震動速度，再確定最終的爆破設計方案，為居民房屋的安全提供了保障，改善了企業與居民關系，加快了企業建設進程。

參考文獻：

［1］申旭鵬.研山鐵礦臺階炮孔爆破地表質點振速峰值預測方法研究［D］.北京：北京科技大學，2012：2－3.

［2］劉殿中，楊仕春.工程爆破實用手冊［M］.北京：冶金工業出版社，2004.

［3］沈蔚，徐全軍，季茂榮，等.中深孔爆破震動參數的BP神經網絡預報［J］.爆炸與沖擊，2002，22（4）：353 －357.

［4］徐全軍，張慶明，惲壽榕.爆破地震峰值的神經網絡預報模型［J］.北京理工大學學報，1998，18（4）：472 －475.

［5］Mostafa Tantawy Mohamed.Artificial neural network for predic－tion and control of blasting vibrations in Assiut （Egypt）limestone quarry［J］.International Journal of RockMechanics＆MiningSciences，2009，46：426 －431.

［6］Manoj Kh，Singh TN.Prediction of blast induced ground vibrations and frequency in opencast mine：a neural network approach［J］.Journal of Sound and Vibration，2006 （289）：711－725.

［7］楊佑發，崔波.爆破震動速度峰值的預測［J］.震動與沖擊，2009，28（10）：195－198.

［8］陳德志，朱瑞賡.基于BP神經網絡的路塹爆破對鄰近民房安全預測的研究［J］.巖石力學與工程學報，2002（2）：51－54.

［9］張天軍，馬銳，喬寶明，等.爆破震動中薩道夫斯基拓展式的回歸分析［J］.湖南科技大學學報：自然科學版，2012（3）：12－16.

中圖分類號：TD76

文獻標識碼：B

文章編號：1004－2660（2015）01－0001－05

收稿日期：2015－01－20.

作者簡介：李小武（1980－），男，湖南人，工程師.主要研究方向：采礦工程.

Study on the Prediction Method of Vibration Velocity in Bench Blasting

LI Xiao－wu，ZHOU Ming，HU Tao，DAI Yu－hao，HE Huang－bing
（Kunming Engineering＆Research Institute of Nonferrous Metallurgy Co.Ltd.，Kunming 650051，China）

Abstract：As cracks were observed in the wall of resident houses near the open stope，vibration measurement on site was carried out.The reliability of traditional Sadov’s linear regression and vibration velocity prediction by BP neural network was examined.The blasting vibration particle velocity prediction of by BP neural network was adopted and the blasting vibration was reduced by adjusting the blasting design，thus ensuring the housing security. Key words：mine blasting；blasting vibration；neural network prediction；housing security