非連通圖L6∪G的優美標號

(華東交通大學理學院, 江西 南昌330013)

·基礎學科·

非連通圖L6∪G的優美標號

吳 躍 生

(華東交通大學理學院, 江西 南昌330013)

討論非連通圖L6∪G的優美性，給出了非連通圖L6∪G是優美圖的4個充分條件。

優美圖;交錯圖；非連通圖;優美標號;梯圖

1 引言與概念

圖的優美標號問題是組合數學中一個熱門課題[1-20]。

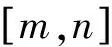
本文討論了非連通圖L6∪G的優美性。

定義2[1]L2m=P2×Pm稱為梯圖。

梯圖L6存在如圖1所示的優美標號。

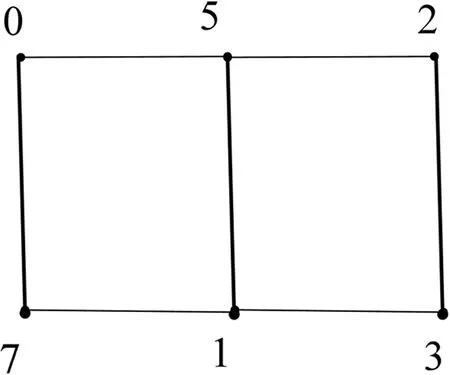
圖1 梯圖L6的優美標號

梯圖L6存在如圖1所示的特征為2且缺標號值4，6的交錯標號。

2 主要結果及其證明

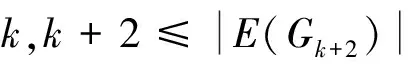
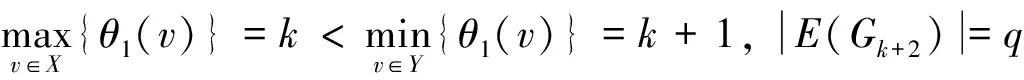
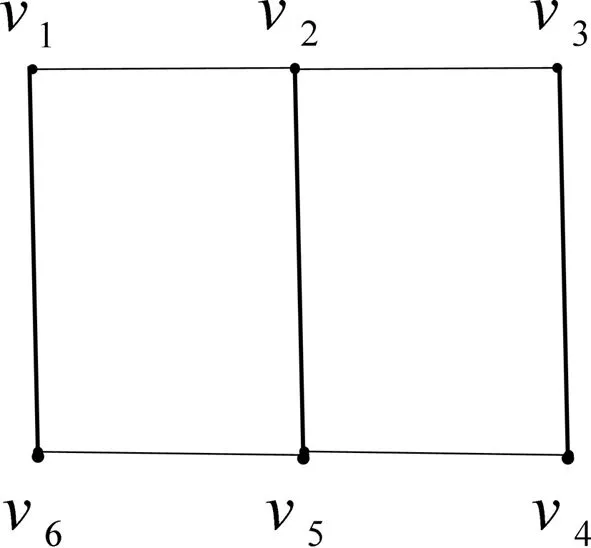
圖2 圖L6

定義L6∪Gk+2的頂點標號θ為：

θ(v1)=k+9，θ(v2)=k+3，θ(v3)=k+5，θ(v4)=k+4，θ(v5)=k+7,θ(v6)=k+2，

下面證明θ是非連通圖L6∪Gk+2的優美標號。

1)θ:V(L6)→[k+2,k+7]∪{k+9}-{k+6}是雙射，

θ:X→[0,k]是單射(或雙射)，θ:Y→[k+8,q+7]-{k+9}是單射(或雙射);

所以，θ:V(L6∪Gk+2)→[0,q+7]-{k+1，k+6}是單射(或雙射)。

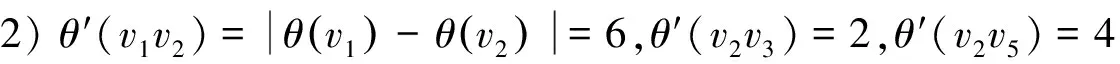
θ′(v3v4)=1,θ′(v4v5)=3,θ′(v6v5)=5,θ′(v6v1)=7，

θ′:E(L6)→[1,7]是雙射，θ′:E(Gk+2)→[8,q+7]是雙射，

所以θ就是非連通圖L6∪Gk+2的缺k+1和k+6標號值的優美標號。

令X1=X∪{v2,v4,v6}，Y1=Y∪{v1,v3,v5}，

則有

所以，θ就是非連通圖L6∪Gk+2的特征為k+4,且缺k+1和k+6標號值的交錯標號。 證畢。

注意到：k+6=(k+4)+2,連續應用定理1。

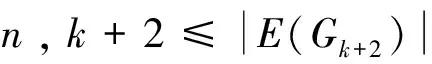
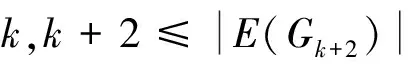
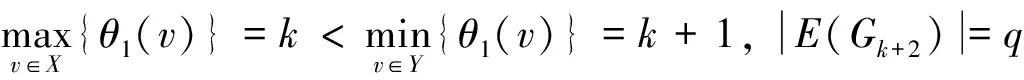
定義L6∪Gk+2的頂點標號θ為：

θ(v1)=k+6，θ(v2)=k+3，θ(v3)=k+5，θ(v4)=k+4，θ(v5)=k+9,θ(v6)=k+2，

下面證明θ是非連通圖L6∪Gk+2的優美標號。

1)θ:V(L6)→[k+2,k+6]∪{k+9}是雙射，

θ:X→[0,k]是單射(或雙射);θ:Y→[k+8,q+7]-{k+9}是單射(或雙射);

所以θ:V(L6∪Gk+2)→[0,q+7]-{k+1，k+7}是單射(或雙射)。

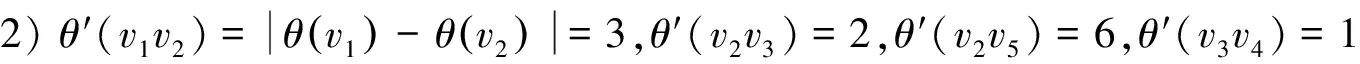
θ′(v4v5)=5,θ′(v6v5)=7,θ′(v6v1)=4，

θ′:E(L6)→[1,7]是雙射，θ′:E(Gk+2)→[8,q+7]是雙射，

所以θ就是非連通圖L6∪Gk+2的缺k+1和k+7標號值的優美標號。

令X1=X∪{v2,v4,v6}，Y1=Y∪{v1,v3,v5}，

則有

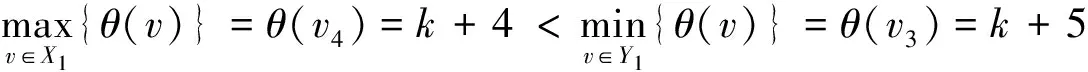
所以，θ就是非連通圖L6∪Gk+2的特征為k+4,且缺k+1和k+7標號值的交錯標號。 證畢。

定義L6∪Gk+3的頂點標號θ為：

θ(v1)=k+7，θ(v2)=k+4，θ(v3)=k+6，θ(v4)=k+5，θ(v5)=k+10,θ(v6)=k+3。

下面證明θ是非連通圖L6∪Gk+3的優美標號。

1)θ:V(L6)→[k+3,k+7]∪{k+10}是雙射，

θ:X→[0,k]是單射(或雙射)，θ:Y→[k+8,q+7]-{k+10}是單射(或雙射);

所以θ:V(L6∪Gk+3)→[0,q+7]-{k+1，k+2}是單射(或雙射)。

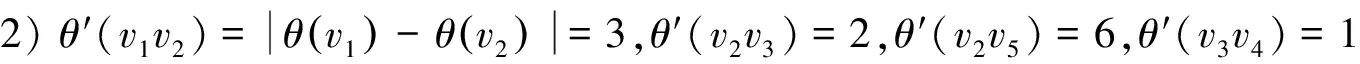
θ′(v4v5)=5,θ′(v6v5)=7,θ′(v6v1)=4，

θ′:E(L6)→[1,7]是雙射，θ′:E(Gk+3)→[8,q+7]是雙射，

所以θ就是非連通圖L6∪Gk+3的缺k+1和k+2標號值的優美標號。

令X1=X∪{v2,v4,v6}，Y1=Y∪{v1,v3,v5}，

則有

所以，θ就是非連通圖L6∪Gk+3的特征為k+5,且缺k+1和k+2標號值的交錯標號。 證畢。

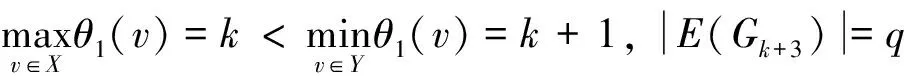
定義L6∪Gk+3的頂點標號θ為：

θ(v1)=k+1，θ(v2)=k+4，θ(v3)=k+2，θ(v4)=k+3，θ(v5)=k+10,θ(v6)=k+5。

下面證明θ是非連通圖L6∪Gk+3的優美標號。……