關于修正的一維分子晶體模型的孤子激發(fā)
李琴蘭,陳 浩
(華南師范大學物理與電信工程學院,廣州510006)
1 引 言
在極性晶體中運動的電子,其庫侖勢使周圍正負離子移位而產(chǎn)生極化,形成一個圍繞電子的極化場. 極化場又反過來作用于電子,使其能量和狀態(tài)等發(fā)生改變,并伴隨著電子在晶格中運動這樣一個相互作用的整體就是極化子. 極化子效應降低電子的能量,并使電子有效質(zhì)量增加. 幾十年來極化子問題一直在固體物理中扮演著相當重要的角色[1-4]. 近年來,由于低維系統(tǒng)非線性元激發(fā)的研究進展,重新引起人們對于一維極化子理論的興趣. 而一維分子晶體模型中孤子激發(fā)態(tài)的存在也一直引起人們的重視,并已做過廣泛的研究. 江濤[5]研究了一維分子晶體的極化子-孤立子運動,得到了帶有孤立波形式的兩類新的極化子- 孤立子解. 任學藻[6]等采用相干態(tài)展開法研究了一維分子晶體模型處于基態(tài)的極化子滿足的帶有積分形式的非線性薛定諤方程及其定態(tài)孤子解. 陳浩[7]等研究了Aharonov -Bohm 對環(huán)上帶有色散項的分子晶體模型的光學極化子的影響.李圳[8]等研究了一維分子晶體模型中立方型相互作用引起的孤子激發(fā). 本文研究關于修正的一維分子晶體模型的孤子激發(fā)解. 該修正解是在文獻[8]的模型基礎上加入了本征值平方項后得到的,通過分析本征值平方項和立方型相互作用對孤子激發(fā)的峰寬、峰值和電子自陷勢阱的影響,我們可以看到本征值平方項有利于立方型相互作用的一維分子晶體模型中孤子的激發(fā),改進了立方型相互作用對一維分子晶體模型孤子的彌散效應. 在忽略立方型相互作用和本征值平方項的影響后,該解與通常極化子解[1]一致.
2 運動方程和解
考慮立方型相互作用后的一維分子晶體模型的Hamiltonian 量為:

這一Hamiltonian 描述了一維系統(tǒng)中電子通過畸變與晶格光學振動發(fā)生相互作用,其中y 和m 分別是電子的坐標和質(zhì)量,a 表示晶格間距,Rn= na 表示第n 個分子的位置,un表示第n 個分子
根據(jù)Holstein,我們可假定波函數(shù):
滿足Schrodinger. 這里an依賴于時間t 和晶格振動位移un,表示電子在第n 格點上的概率幅;φn(y,un)為第n 格點上的局域化的分子軌道,滿足方程:

式中本征值E(un)只與分子振動的位移量un有關. 與往常的取線性近似不同,為了得到更準確的結果,我們將本征值取到平方項,即:

由式Schrodinger 方程,得到an的運動方程:
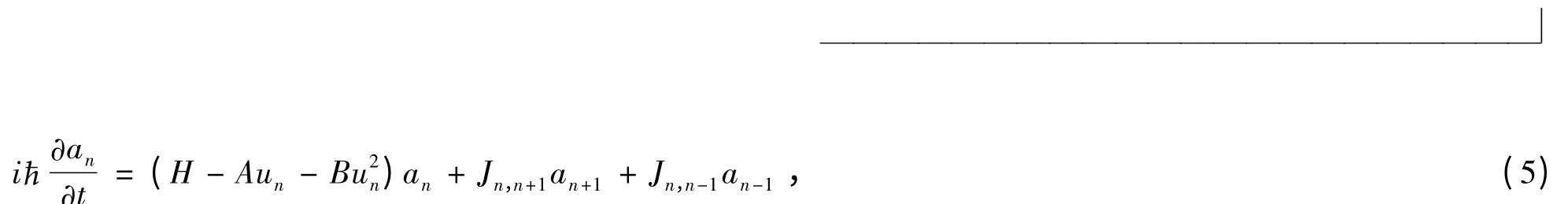
式中
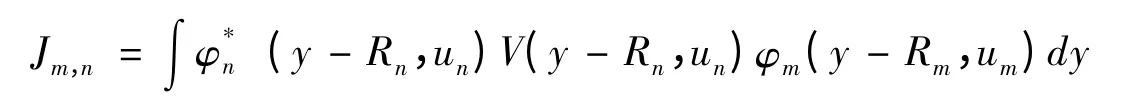
是雙中心交疊積分. - Aun-項代表電子與晶格間的相互作用勢. 忽略Jn,n=1對un的依賴. 設Jn,n+1= - J,則:

取絕熱近似,即略去式(6)中的晶格振動動能項,則得:
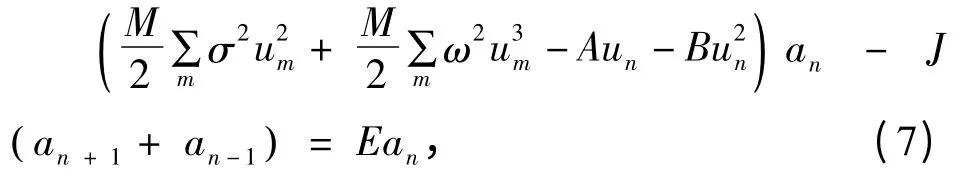

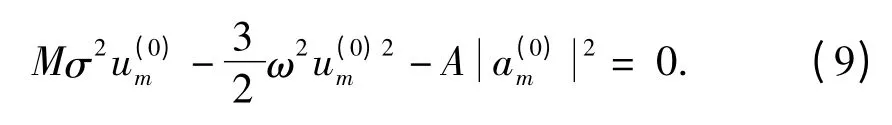
在ω2<<σ2時,上式的解為:
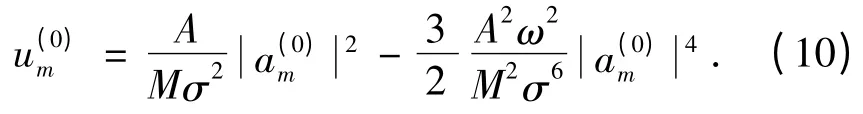
當a(0)n是n 的緩變函數(shù)時,可做下列連續(xù)化近似:

將式(10)、(11)代入式(7)可化解為:


3 討 論
3.1 當ω2= 0 ,B = 0 時,即不考慮了立方型相互作用和本征值平方項時,孤子激發(fā)解回復于通常的極化子解[1]:

此時孤子的峰寬、峰值為(15)、 (17)式.由圖3 可知,此時孤子激發(fā)的峰寬最窄,峰值最大,孤子特征最明顯.
3.2 當ω2≠0 ,B = 0 時,由文獻[8]可知,正比于ω2的項(即立方型相互作用項)是孤子的彌散項.
3.3 當ω2≠0 ,B ≠0 時,令α =,β =則式(12)化為:

該方程的解為:

即在考慮立方型相互作用和本征值平方項后一維分子晶體模型的孤子激發(fā)的修正解可表述為式(13),該孤子激發(fā)的峰寬和峰值變?yōu)?


圖1 孤子的寬度隨β 的變化Fig.1 The change of the width of the soliton with the β

圖2 孤子的峰值隨β 的變化Fig.2 The change of the peak of the soliton with the β
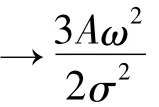
以上是從數(shù)學角度分析了立方型相互作用和本征值平方項對一維分子晶體模型的孤子激發(fā)的影響,得到了有利于孤子激發(fā)的條件和不利于孤子激發(fā)的條件. 下面從物理意義上分析,理解他們對孤子激發(fā)的影響.
當ω2≠0 ,B ≠0 時,自陷態(tài)晶格振動位移為:

相應的電子自陷勢阱則為:
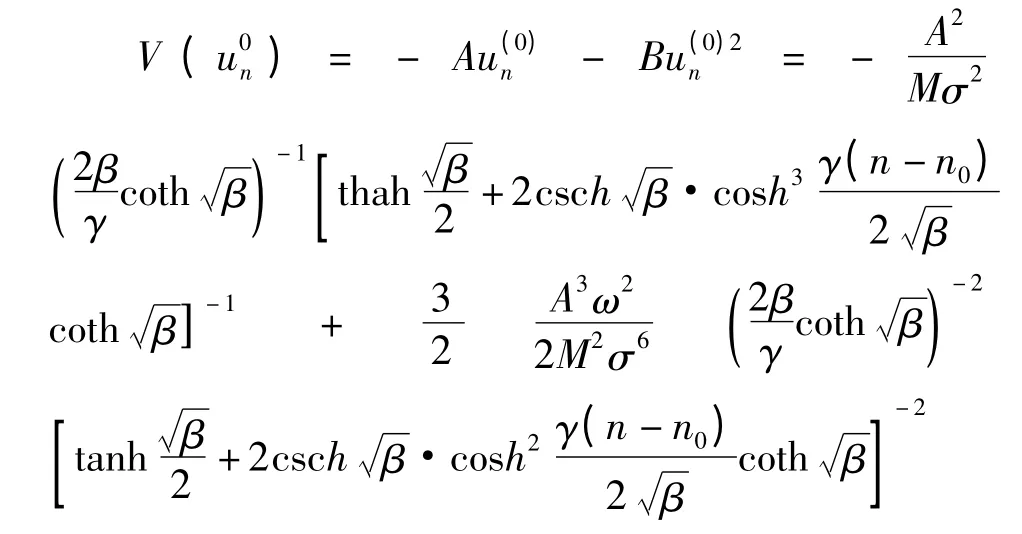


圖3 β 取不同值時孤子解的比較Fig.3 The compare of solutions when β takes different values
在這里取A = 2,ω2=,分別畫出的電子自陷勢阱圖,如圖4.

圖4 β 取不同值時電子自陷勢阱圖的比較Fig.4 The compare of the electron’s selftrapped potential well when β takes different values
4 結 論
在考慮立方型相互作用和本征值平方項后一維分子晶體模型的孤子激發(fā)的修正解跟通常孤子解相比較有很大的不同,他的孤子特征變的很不明顯.

[1] Holstein T. Studies of polaron motion. Part I. The molecular crystal model[J]. Ann. Phys.,1959,8:325.[2] Chen H,Chen Y. On optical polarons in one dimensional molecular - crystal chains[J]. Chinese Phys.Lett.,1996,13:617.
[3] Zhang C L,Jeckelmann E,White S R. Dynamical properties of one - dimensional Holstein model[J].Phys. Rev. B,1999,60(20):14092.
[4] Zhao C L,Wang L L,Zhao L L. The properties of ground state of polaron in quantum disk in finite depth potential well[J]. J. At. Mol. Phys.,30(4):637(in Chinese)[趙翠蘭,王麗麗,趙麗麗. 有限深勢阱里量子盤中極化子的基態(tài)性質(zhì)[J]. 原子與分子物理學報,2013,30(4):637]
[5] Jiang T. Polaron solitons motion in one -dimensional molecular crystals[J]. J. Henan Univ.:Natural Science Edition,2003,33(3):17(in Chinese)[江濤.一維分子晶體的極化子-孤立子運動[J]. 河南大學學報:自然科學版,2003,33(3):17][6] Ren X Z,Liao X,Liu T,et al. Polaron of one -dimensional molecular crystals[J]. J. At. Mol. Phys.,2006,23(4):616(in Chinese)[任學藻,廖旭,劉濤,等. 一維分子晶體中的極化子[J]. 原子與分子物理學報,2006,23(4):616]
[7] Chen H,Chen Y. Influence of the Aharonov -Bohm flux on the optical polarons in the molecular - crystal model with the dispersion term in a ring[J]. Solid State Commun.,1998,105(8):537.
[8] Li Z,Chen H. Soliton excitation of a one-dimensional molecular-crystal model with a cubic interaction term[J]. J. South China Normal Univ.:Natural Science Edition,2011,(1):62(in Chinese)[李圳,陳浩.一維分子晶體模型中立方型相互作用引起的孤子激發(fā)[J]. 華南師范大學學報:自然科學版,2011,(1):62]
[9] Li Z Z. Solid Theory[M]. 2nded. Beijing:Higher education Press,2002:363(in Chinese)[李正中. 固體理論[M].2 版. 北京:高等教育出版社,2002:363]

