多入單出正交空時分組碼系統的調制識別

錢國兵李立萍 郭亨藝

(電子科技大學信息工程系 成都 611731)

多入單出正交空時分組碼系統的調制識別

錢國兵*李立萍 郭亨藝

(電子科技大學信息工程系 成都 611731)

在現代無線通信系統中，采用正交空時分組碼(STBC)的多天線發射技術是提高通信速率和可靠性，并且能夠實現簡單譯碼的關鍵技術。該文針對瑞利信道系統模型，提出一種適用于多入單出正交空時分組碼(OSTBC)的調制識別算法。該算法通過對接收到的數據進行重排，將多入單出的系統模型轉化為類似多入多出的系統模型，并且根據信源的特殊性用最大似然的思想實現調制類型的識別。仿真結果驗證了所提算法的有效性。

無線通信；調制識別；多入單出；正交空時分組碼

1 引言

多天線發射技術是現代無線通信中用來提高通信速率和可靠性的重要技術手段。空時分組碼(Space-Time Block Code, STBC)[1?3]是多天線通信系統的主要編碼方式，其中正交空時分組碼因為能夠提供滿分集和譯碼簡單被廣泛使用。通信系統參數盲估計是一個重要的研究課題，廣泛應用于軍事及民用領域[4?6]，其中調制類型的盲識別具有重要的理論和現實意義，已引起國內外學者的關注。

2009年，Choqueuse等人[7]針對多入多出(MIMO)系統提出基于獨立分量分析(ICA)的最大似然調制識別算法，該算法可以看作是在該系統下調制識別算法性能的上界，然而該算法只能適用于空分復用的情形卻不能適用于空時分組碼系統。2012年，Hassan等人[8]利用調制信號高階累積量特征提出基于神經網絡的識別算法，該算法能較好地適用于空間相關的信道模型，然而同樣不能適用于空時分組碼系統。同年，Mühlhaus等人[9]利用調制信號高階累積量特征提出基于歐氏距離最小準則的識別算法。2013年，文獻[10]在文獻[9]基礎上提出基于調制信號高階累積量特征的最大似然識別算法，該算法計算復雜度遠低于文獻[7]提出的調制識別算法，然而同樣不能適用于空時分組碼系統。Luo等人[11,12]于2012年和2013年分別提出基于特征函數和多維ICA的最大似然調制識別算法，該算法能夠較好地適用于空時分組碼系統，然而只能有效地識別復調制(≥4PSK, ≥4QAM)，卻不能適用于PAM等實調制類型。此外，這些方法都只能適用于多根接收天線的情形，目前還沒有提出適用于多天線發射單天線接收情形下的調制識別算法。

本文針對正交空時分組碼系統，提出一種適用于單根接收天線情形下的調制識別算法。首先，我們將接收到的數據進行重排，然后提出基于最大似然的調制識別算法。考慮到實際情形中信道是未知的，我們先用二階統計量的方法[13]來預估信道，對于存在剩余模糊的編碼，再用ICA算法中[14]帩度最大化的思想來去掉部分模糊，然后證明似然函數對剩余的模糊不敏感，因而可以用估計出來的信道進行調制識別。最后，仿真實驗驗證了本文算法的有效性。

2 系統模型

在正交空時分組碼系統中，由星座M(假設其具有M個狀態)調制后的每n個符號被分為一組，記為sv=[s1,s2,…,sn]T。向量sv被編碼為一個nt×l(nt為發射天線個數，l為分組長度)維的復矩陣[3]：

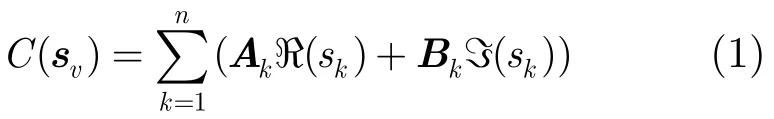
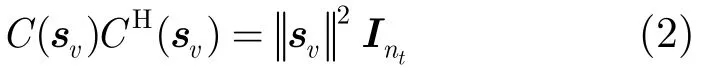
且滿足：其中Ak和Bk均為nt×l維的空時編碼矩陣，?(·)和?(·)分別表示取變量的實部和虛部。

空時分組碼經天線發射后在只有單根接收天線情況下的信道傳輸模型為[3]

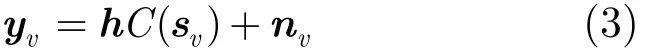
其中向量yv表示第v個組接收到的信號；向量h為信道傳輸向量，在本文中假設其為頻率平坦衰落瑞利信道；nv為每個分組上的加性高斯白噪聲，其在時間和空間上不相關；傳輸符號的功率假設是經過歸一化的，即E(|sv|2)=1。這里需要聲明的是，歸一化的假設是很常見的，例如在參考文獻[7-12]中。

3 基于最大似然的調制分類器

本文將yv的實部和虛部拼接為一個向量，則

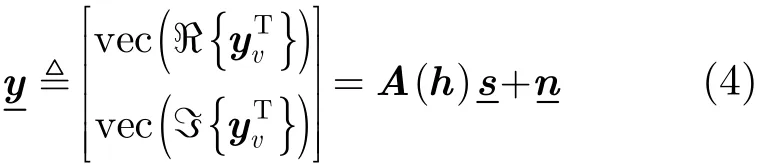
其中vec(·)表示向量化。

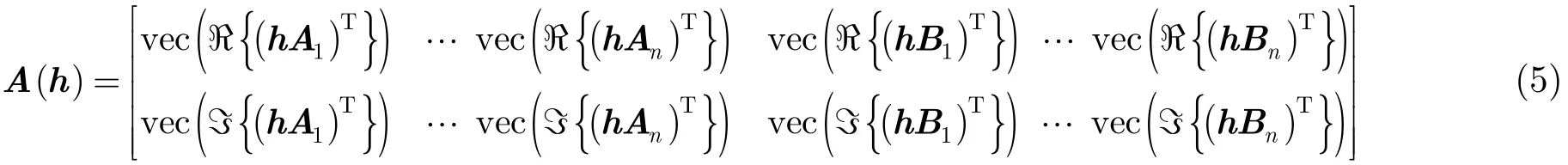
為2l×2n維的虛擬信道矩陣。

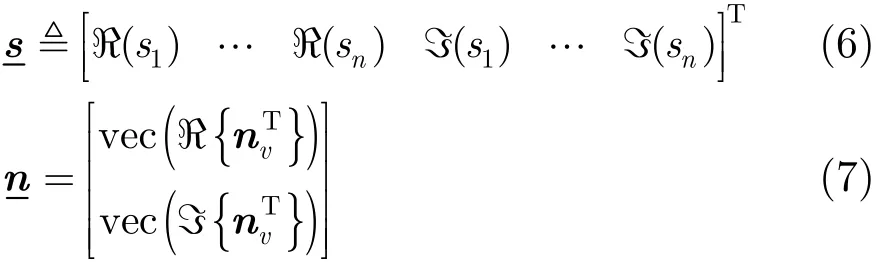
根據上述單個天線下的系統模型表達式，基于最大似然的調制類型識別可以表達為

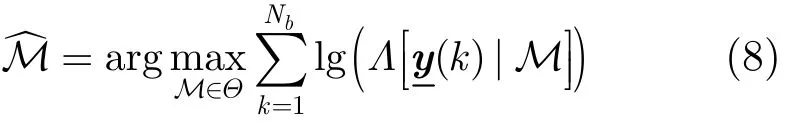
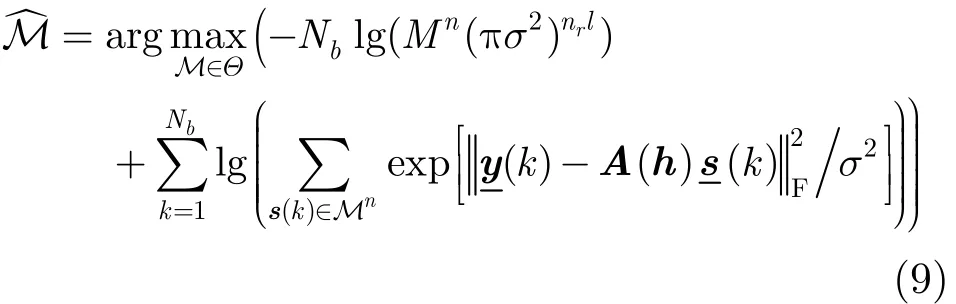
其中σ2表示噪聲平均功率。

在實際場景中，信道信息往往是未知的。這里先利用正交空時分組碼的特性用二階統計量的方法[13]來預估信道(該方法只能適用于正交空時分組碼是由于其依賴于編碼的正交特性和特有的空時冗余)，對于存在剩余模糊的編碼，再用帩度最大化的思想來去掉部分模糊。具體方法如下：

(1)如果ΦT(I2K?R)Φ的主特征值是m重的(m取值由具體的正交空時分組碼決定[13])，那么=Uw，其中4nl×2nt維的矩陣Φ為h與vec{A(h)}之間的過渡矩陣，其第k列構造方式為vec{A(ek)}, ek為第k個元素為1而其余元素為0的2nt維的行向量，R為接收數據按式(4)重排后的自相關矩陣，U為主分量特征向量張成的空間，w=[w1… wm]T為待估實向量。此時，

由于大多數的數字調制(PAM,PSK,QAM)的帩度為負值[15]，所以最大化估計出來的源信號的帩度的絕對值等價于最小化估計出來的源信號的帩度。而s?由w決定，所以最小化s?帩度就等價于

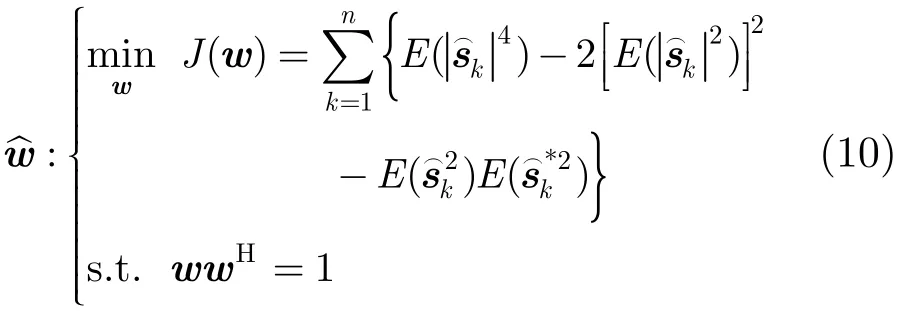
我們可以采用經典的梯度下降法來優化上面的代價函數，其中

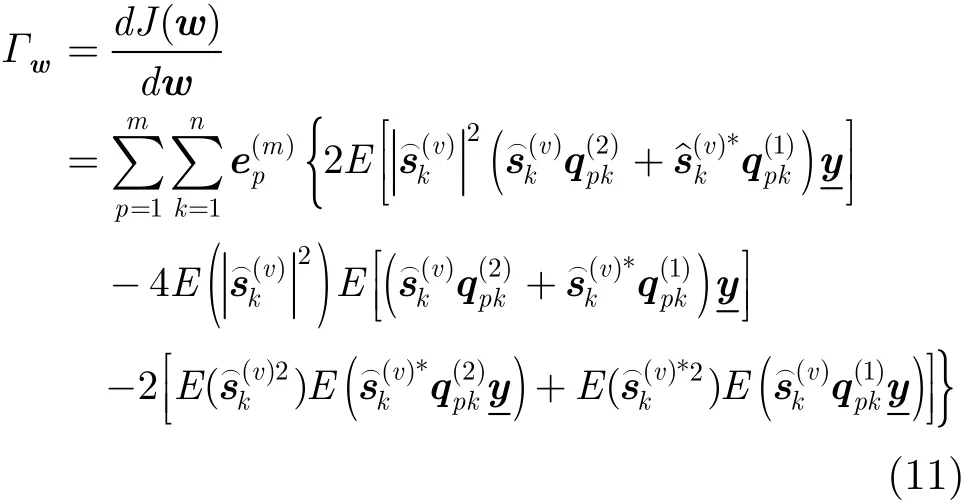
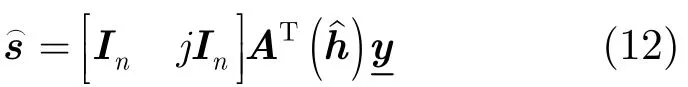
在無噪聲情況下，估計出來的源信號和真實的源信號有一個置換，幅度，相位的模糊，即

其中D為對角矩陣，其對角線上元素分別為ejθ1,ejθ2,…,ejθn,P為交換矩陣。

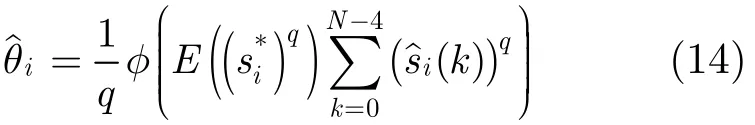
其中φ(·)表示取一個復數的相位角，系數q與調制類型有關，對于PAM調制，星座的旋轉對稱角度為π，所以q=2；對于M-PSK調制，q=M；對于正方形或矩形M-QAM調制，q=4。定義：為對角矩陣，其對角線上元素分別為,,…,;q為對角矩陣，其對角線上元素分別為ej2πρ1/q, ej2πρ2/q,…,ej2πρn/q，則D=q，其中q為剩余的相位模糊，ρ1,ρ2,…,ρn均為整數，取值范圍為?(M ?1)～(M?1),M為調制類型M的狀態數。接下來，我們來證明似然函數對剩余的相位模糊并不敏感。

由式(13)可得

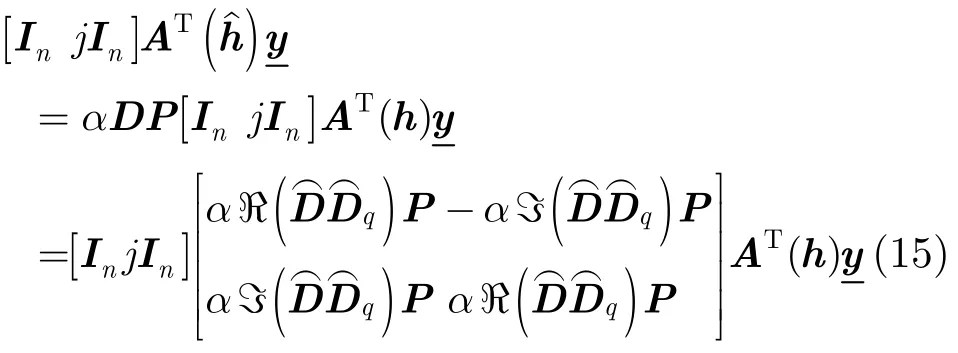
所以

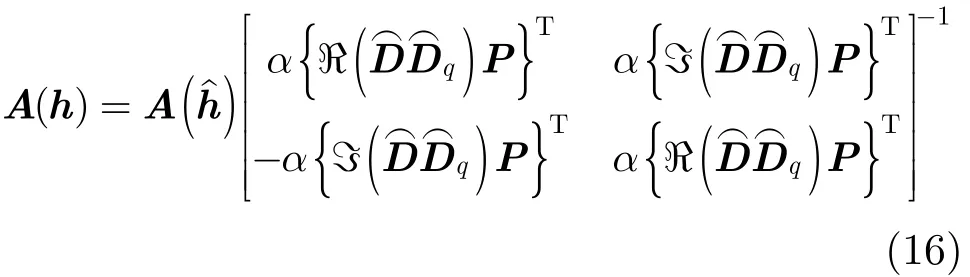
此時的似然函數可以寫成：

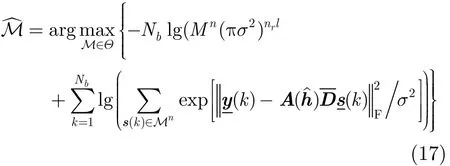
又由于s(k)∈Mn時，，因此似然函數可以進一步化簡為

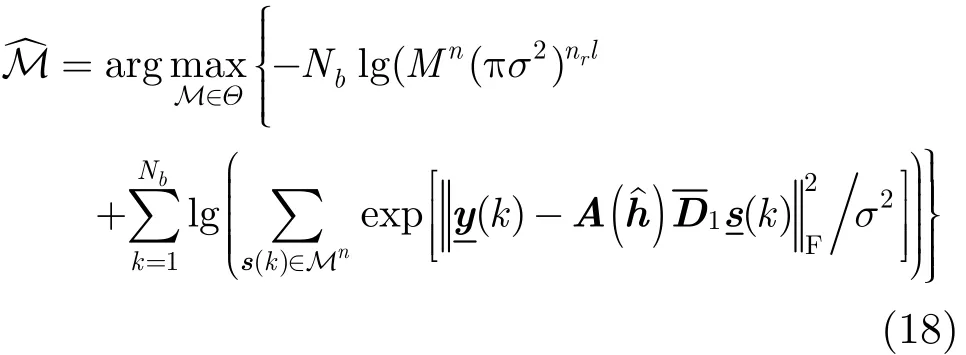
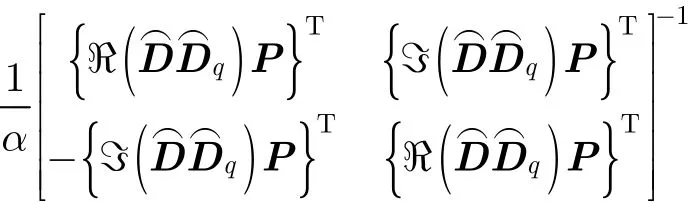
和

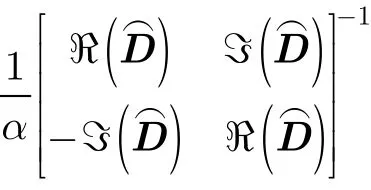
從以上證明過程中可以看出，似然函數對剩余的相位模糊并不敏感。

4 仿真

本文采用平均正確識別概率為指標來衡量算法性能，集合Θ由BPSK, 4PSK, 16PSK和16QAM 4種調制組成，所有仿真是在以下條件下進行：(1)瑞利信道；(2)噪聲在空間和時間上不相關，方差為2σ；(3)單根天線接收，且接收到的空時分組碼的組數Nb為512；(4)信噪比定義為[1,7]：SNR=10lg(P2/σ)，其中P為發射端天線總功率。在每個信噪比下進行500次蒙特卡洛仿真實驗。

在仿真實驗1和仿真實驗2中分別采用Alamouti編碼和3/4碼率的正交空時分組碼[3]，此外，為了避免梯度下降法收斂到局部極值，在估計信道時對w賦多個初值，最終收斂時使代價函數最小的w值即認為是使代價函數收斂到全局極值的w。

仿真實驗1 多入單出系統采用Alamouti編碼時的正確識別概率

圖1是多入單出(MISO)系統采用Alamouti編碼時本文所提出的調制識別算法的性能曲線。圖1(a)是發射端符號采用BPSK調制時的識別概率，從中可以看出，當信噪比大于或等于1 dB時正確識別的概率能達到100%，而在低信噪比下，可能會將調制類型誤識別為QPSK或者16QAM；圖1(b)是發射端符號采用QPSK調制時的識別概率，從中可以看出當信噪比大于或等于7 dB時，正確識別的概率能達到100%，而在低信噪比下，容易將調制類型誤識別為16QAM；圖1(c)是發射端符號采用16PSK調制時的識別概率，從中可以看出當信噪比大于或等于7 dB時，正確識別的概率能達到100%，而在低信噪比下，容易將調制類型誤識別為QPSK或者16QAM；圖1(d)是發射端符號采用16QAM調制時的識別概率，從中可以看出當信噪比大于或等于7 dB時，正確識別的概率能達到100%，而在低信噪比下，容易將調制類型誤識別為QPSK。

仿真實驗2 多入單出系統采用3/4碼率的正交空時分組碼的正確識別概率

圖2是多入單出系統采用3/4碼率的正交空時分組碼時本文所提出的調制識別算法的性能曲線。圖2(a)是發射端符號采用BPSK調制時的識別概率，從中可以看出當信噪比大于或等于1 dB時，正確識別的概率能達到100%，而在低信噪比下，容易將調制類型誤識別為QPSK；圖2(b)是發射端符號采用QPSK調制時的識別概率，從中可以看出當信噪比大于或等于5 dB時，正確識別的概率能達到100%，而在低信噪比下，容易將調制類型誤識別為16QAM；圖2(c)是發射端符號采用16PSK調制時的識別概率，從中可以看出當信噪比大于或等于5 dB時，正確識別的概率能達到100%，而在低信噪比下，容易將調制類型誤識別為QPSK或者16QAM；圖2(d)是發射端符號采用16QAM調制時的識別概率，從中可以看出當信噪比大于或等于3 dB時，正確識別的概率能達到100%，而在低信噪比下，容易將調制類型誤識別為QPSK。對比圖1可以看出，本文所提出的調制識別算法在系統采用3/4碼率的正交空時分組碼時性能要優于采用Alamouti編碼時的性能。

5 結束語

本文提出一種適用于多入單出正交空時分組碼系統的調制識別算法。首先，利用正交空時分組碼在時間和空間上的特殊冗余性，將多入單出系統模型轉換為多入多出的系統模型。然后在該模型上利用等效信源的特殊性，提出了基于最大似然的調制識別算法。仿真結果驗證了本文算法的有效性。

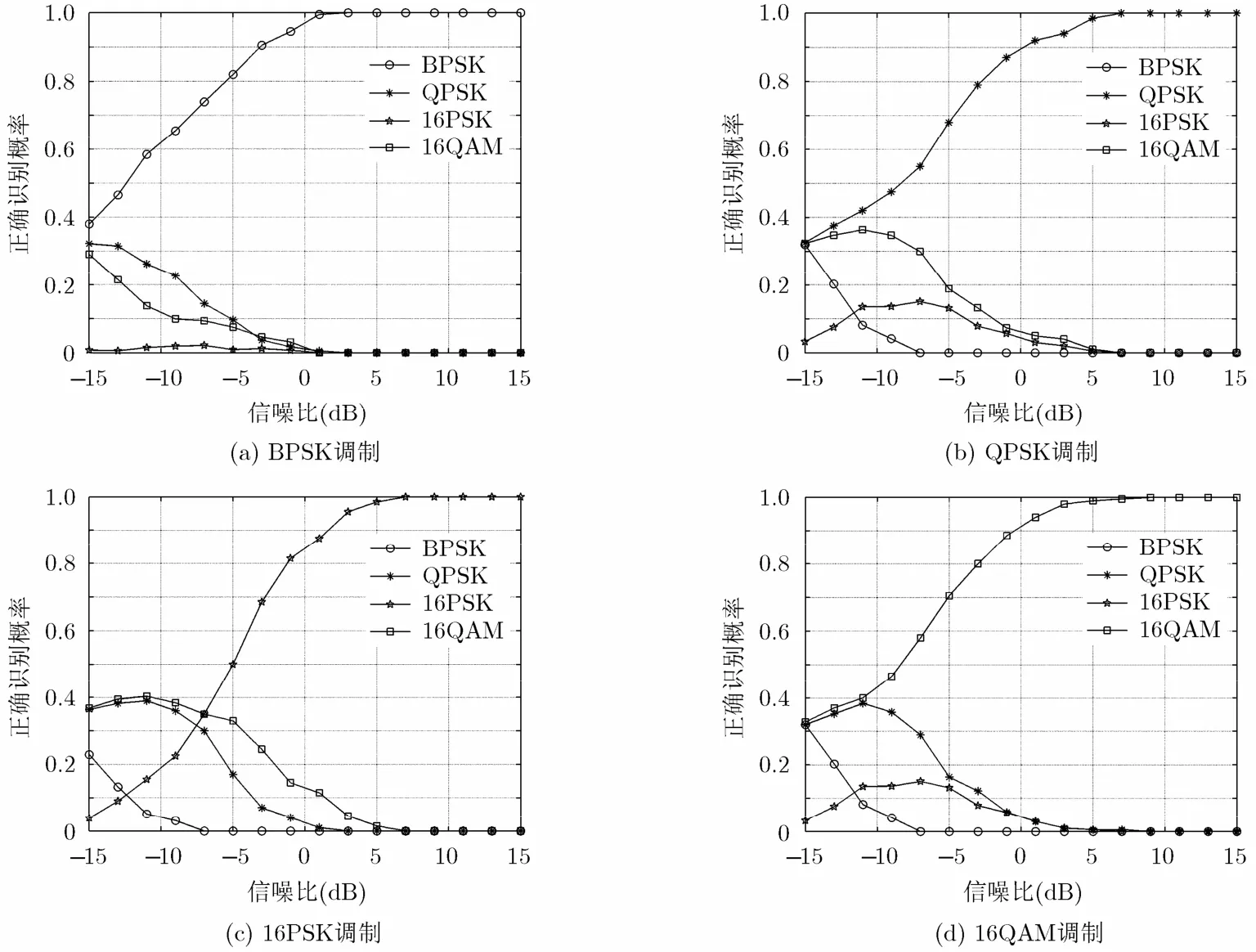
圖1 多入單出系統采用Alamouti編碼時各種調制類型的正確識別概率

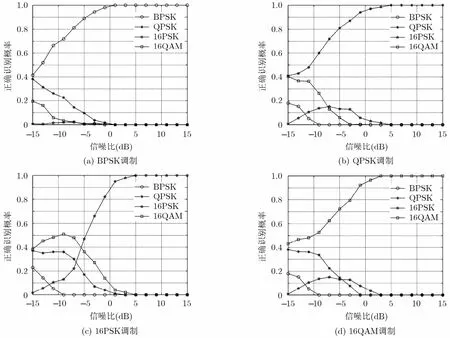
圖2 多入單出系統采用3/4碼率的正交空時分組碼時各種調制類型的正確識別概率

[1] Vucetic B and Yuan J. Space-time Coding[M]. New York: John Wiley & Sons, 2003, Chapters, 3-5.

[2] Jafarkhani H. Space-time Coding: Theory and Practice[M]. New York: Cambridge University Press, 2005: 45-53.

[3] Larsson E G and Stoica P. Space-time Block Coding for Wireless Communications[M]. New York: Cambridge University Press, 2008: 79-95.

[4] 付衛紅, 楊小牛, 劉乃安. 基于四階累積量的穩健的通信信號盲分離算法[J]. 電子與信息學報, 2008, 30(8): 1853-1856. Fu Wei-hong, Yang Xiao-niu, and Liu Nai-an. Robust algorithm for communication signal blind separation fourthorder-cumulant-based[J]. Journal of Electronics & Information Technology, 2008, 30(8): 1853-1856.

[5] 李進, 馮大政, 房嘉奇. MIMO 通信系統中 QAM 信號的快速半盲均衡算法研究[J]. 電子與信息學報, 2013, 35(1): 185-190. Li Jin, Feng Da-zheng, and Fang Jia-qi. Study of fast semi-blind equalization algorithm for MIMO systems with QAM signal[J]. Journal of Electronics & Information Technology, 2013, 35(1): 185-190.

[6] Qian G, Li L, Luo M, et al.. Blind recognition of space-time block code in MISO system[J]. EURASIP Journal on Wireless Communications and Networking, 2013, 164(1): 1-12.

[7] Choqueuse V, Azou S, Yao K, et al.. Blind modulation recognition for MIMO systems[J]. MTA Review, 2009, 19(2): 183-196.

[8] Hassan K, Dayoub I, Hamouda W, et al.. Blind digital modulation identification for spatially-correlated MIMO systems[J]. IEEE Transactions on Wireless Communications, 2012, 11(2): 683-693.

[9] Mühlhaus M S, ?ner M, Dobre O A, et al.. Automatic modulation classification for MIMO systems using fourth-order cumulants[C]. Vehicular Technology Conference (VTC Fall), Quebec City, 2012: 1-5.

[10] Muhlhaus M, Oner M, Dobre O, et al.. A low complexity modulation classification algorithm for MIMO systems[J]. IEEE Communications Letters, 2013, 17(10): 1881-1884.

[11] Luo M, Li L, and Tang B. A blind modulation recognition algorithm suitable for MIMO-STBC systems[C]. International Conference on Communications and Information Technology (ICCIT), Chengdu, 2012: 271-276.

[12] Luo M, Li L, Qian G, et al.. A blind modulation identification algorithm for STBC systems using multidimensional ICA [J]. Concurrency and Computation: Practice and Experience, 2013, 26(8): 1490-1505.

[13] Shahbazpanahi S, Gershman A B, and Manton J H. Closed-form blind MIMO channel estimation for orthogonal space-time block codes[J]. IEEE Transactions on Signal Processing, 2005, 53(12): 4506-4517.

[14] Comon P and Jutten C. Handbook of Blind Source Separation: Independent Component Analysis and Applications[M]. Oxford: Academic Press, 2011: 179-226.

[15] Swami A and Sadler B M. Hierarchical digital modulation

classification using cumulants[J]. IEEE Transactions on Communications, 2000, 48(3): 416-429.

[16] Moeneclaey M and De Jonghe G. ML-oriented NDA carrier synchronization for general rotationally symmetric signal constellations[J]. IEEE Transactions on Communications, 1994, 42(8): 2531-2533.

錢國兵： 男，1986年生，博士生，研究方向為盲源分離、通信信號處理.

李立萍： 女，1963年生，教授，博士生導師，主要研究方向為非合作信號處理、高速信號處理、微弱信號檢測與參數估計等.

郭亨藝： 女，1989年生，碩士生，研究方向為通信信號處理.

Modulation Identification for Orthogonal Space-time Block Code in Multiple Input Single Output Systems

Qian Guo-bing Li Li-ping Guo Heng-yi
(Department of Information Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)

In modern wireless communication systems, multiple-antenna-transmitting in association with Orthogonal Space-Time Block Code (OSTBC) is a key technology to improve communication rate, reliability, and decoding complexity. In this paper, a modulation identification algorithm is proposed which is well suitable for the Multiple Input Single Output (MISO)-OSTBC system. First, the MISO system is transformed into a Multiple Input Multiple Output (MIMO) system by reshaping the

data. Then, maximum likelihood based approach is used to identify the modulation. Simulations validate the effectiveness of the proposed algorithm.

Wireless communication; Modulation identification; Multiple Input Single Output (MISO); Orthogonal Space-Time Block Code (OSTBC)

TN92

： A

：1009-5896(2015)04-0863-05

10.11999/JEIT140644

2014-05-14收到，2014-12-26改回

通信信息控制和安全重點實驗室基金(9140C130304120C13064)和國家自然科學基金(61201282)資助課題

*通信作者：錢國兵 shuaiguobing@hotmail.com