某預應力混凝土空心板梁極限承載力計算

高巖淵，洪 濤，張 劍，劉 華

(1.江蘇廣靖錫澄高速公路有限責任公司，江蘇 無錫 214191；2.江蘇省鎮江市工程勘測設計研究院，江蘇 鎮江 212003；3.南京航空航天大學，江蘇 南京 210016；4.中鐵大橋(南京)橋隧診治有限公司，江蘇 南京 210031)

某預應力混凝土空心板梁極限承載力計算

高巖淵1，洪 濤2，張 劍3，劉 華4

(1.江蘇廣靖錫澄高速公路有限責任公司，江蘇 無錫 214191；2.江蘇省鎮江市工程勘測設計研究院，江蘇 鎮江 212003；3.南京航空航天大學，江蘇 南京 210016；4.中鐵大橋(南京)橋隧診治有限公司，江蘇 南京 210031)

橋梁承載能力與損傷程度評定過程中,越來越多的工程師開始考慮橋梁極限承載力的問題，分析橋梁結構的極限承載力不僅可用于極限設計,而且有助于了解結構的破壞形式,準確探知結構在給定荷載下的安全儲備或超載能力,為其安全施工和營運管理提供依據和保障。針對某預應力混凝土空心板梁，結合非線性有限元計算方法，建立了預應力混凝土空心板梁計算模型，同時結合荷載撓度曲線計算結果對其極限承載力進行了研究，所得結論可供工程設計參考。

空心板；預應力；混凝土；極限承載力

在我國的公路與城市道路中，中小跨徑橋梁所占的比重很大，基本上都是采用鋼筋混凝土和預應力混凝土梁板式橋，除小跨徑橋采用整體板外，絕大部分采用多梁式，即在一孔跨中由多根主梁(板)組成上部結構[1-2]，除了簡支的鋼筋混凝土和預應力混凝土簡支梁板橋外，為滿足橋梁的適用性，還有簡支連續橋面以及先簡支后連續多梁式梁板橋[3-4]。對這一類已建橋梁的結構狀況的分析及承載力評估是目前工程上重要和待解決的問題之一[5]，然而，由于此類橋梁都經過長期運營，其邊界條件、材料特性和質量分布等與初始設計相比會有很大出入，有的橋梁甚至出現裂縫等病害[6-9]。橋梁承載能力與損傷程度評定過程中,越來越多的工程師開始考慮橋梁極限承載力的問題[10-11]。分析橋梁結構的極限承載力不僅可用于極限設計,而且有助于了解結構的破壞形式, 準確探知結構在給定荷載下的安全儲備或超載能力,為其安全施工和營運管理提供依據和保障，其越來越受到專家學者的普遍重視。本文根據某預應力混凝土空心板實際結構形式，研究了正確的計算方法，進行了結構極限承載力分析。

1 單元模型

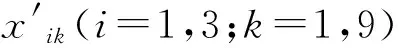
(1)

圖1 實體退化殼單元

相應地，殼元位移場可表示為：

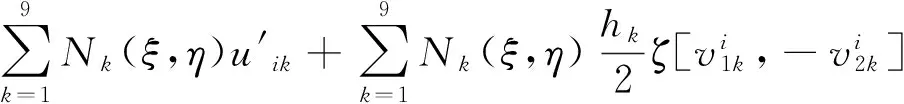
(2)

殼角節點為：

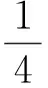
(k=1,3,5,7)

(3)

(4)

中心節點為:

(k=9)

(5)

2 預應力混凝土空心板梁橋的材料非線性特性

2.1 混凝土材料非線性特性

由于殼元需考慮橫向剪切作用，本文選擇了Owen雙參數三軸屈服準則，表達式為：

f(I1,J2)=(αI1+3βJ2)1/2=σ0

(6)

式中，I1為應力張量第一不變量；J2為應力偏量第二不變量；σ0為等效應力，取為單軸抗壓強度fc；α和β為材料參數，由式7并根據單軸抗壓試驗和雙軸等壓試驗標定：

(7)

式中，k=fcc/fc,fcc為雙向抗壓強度。

流動法則采用常用的關聯流動法則。強化準則確定了塑性變形過程中后繼屈服面(加載表面)的運動形式。彈塑性矩陣中的強化參數H′可由有效應力σ對有效塑性應變εp的斜率表示，即：

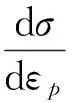
(8)

有效應力σ和有效塑性應變εp的關系采用Madrid線型的單軸應力應變關系推導。基于Madrid線型的單軸應力應變關系式為：

(9)

式中，E0為初始彈性模量；ε0為單軸抗壓強度fc時的總應變，可取為2fc/E0；εe為彈性應變，即等于σ/E0。

混凝土的壓碎斷裂由應變控制，基于Owen理論的混凝土壓碎準則表達式為：

(10)

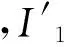
2.2 鋼筋材料非線性特性

在預應力混凝土空心板梁橋的分層殼元法中，鋼筋作為殼元中等效厚度的鋼筋層考慮，假定每一鋼筋層的力學性能是單向的，只能承受沿鋼筋方向的軸向力。采用常用的雙線性關系模擬鋼筋的彈塑性應力應變關系。

3 預應力混凝土空心板梁的基本形式

3.1 構件尺寸

某一預應力混凝土空心板梁全長為19.94 m，混凝土采用40號碎石混凝土。空心板截面如圖2所示，截面鋼筋布置如圖3所示，梁底配筋均為預應力鋼筋，采用先張法預應力，鋼絞線為ASTM A416-90a270級，直徑為15.24 mm。

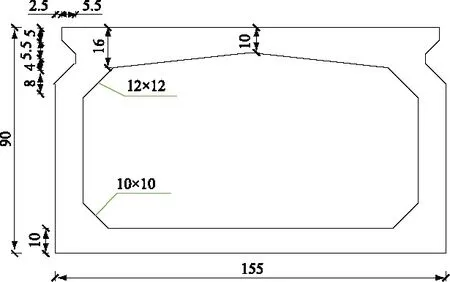
圖2 空心板截面尺寸(cm)

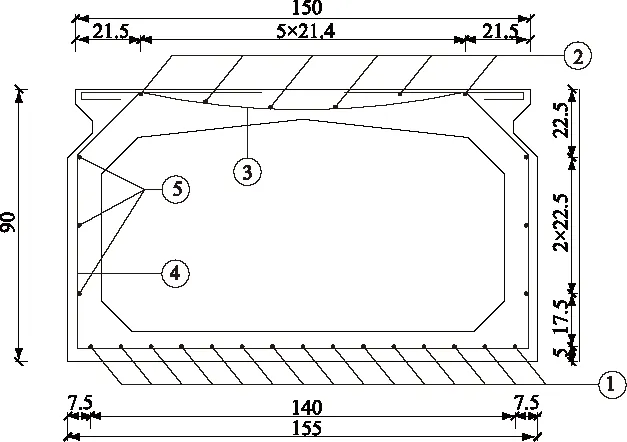
圖3 截面鋼筋布置圖(cm)

3.2 有限元模型和結果分析

采用上述單元模型建立了預應力混凝土空心板梁計算模型，有限元模型和顯示材料的計算模型分別如圖4和圖5所示。采用三分點典型加載形式，每級加載1 t，即單點為0.5 t，荷載-撓度計算結果如圖6所示。

圖4 有限元網格圖 圖5 有限元材料圖

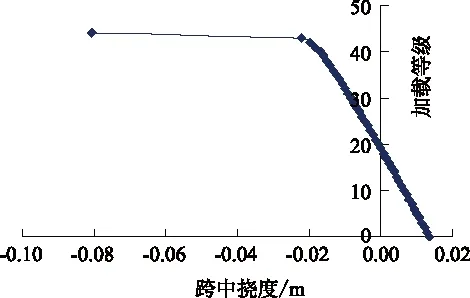
圖6 有限元計算結果

從圖6可以看出，由于預應力混凝土空心板梁預應力效應的存在，初始梁有向上反拱的現象出現，反拱值約為1 cm，隨著加載量的增大，反拱效應逐漸消除。梁在受載初期呈現線彈性工作狀態，其后加載至月40級時，梁體出現非線性。最終加載等級為44級，故極限荷載為44 t。

4 結語

本文針對預應力混凝土空心板梁的受力特點，研究了該結構的非線性有限元計算方法，并且建立了預應力混凝土空心板梁實際計算模型。結果表明，該種結構形式受力性能良好，加載初期梁體反拱并處于線彈性工作狀態，直至加載后期出現非線性。橋梁結構極限承載力不僅可用于極限設計,而且有助于了解結構的破壞形式,準確探知結構在給定荷載下的安全儲備或超載能力,為其安全施工和營運管理提供依據和保障。

[1] 李海光, 項新里, 金群綱, 等. 預應力混凝土連續箱梁維修加固技術措施[J]. 公路交通技術, 2006 (2): 78-81.

[2] 王有志, 孫大海, 徐鴻儒. 鋼筋混凝土簡支板梁式橋病害調查分析與評價[J]. 華東公路, 2002 (4): 3-6.

[3] 陳曉強, 趙佳軍, 吳建平. 板梁結構由鉸縫引起的病害分析及加固改造[J]. 現代交通技術, 2006 (1): 46-48.

[4] 徐強, 段新龍, 劉勝松. 裝配式板(T梁)橋常見病害及對策[J]. 山東交通科技, 2004 (2): 9-10.

[5] 宋一凡, 崔軍, 趙小星, 等. 鋼筋混凝土T 型梁橋裂縫特征參數與結構評估試驗研究[J]. 交通運輸工程學報, 2001, l11(13): 46-49.

[6] 高建華, 梁全福. 橫向體外預應力加固簡支梁橋工藝例談[J]. 中州建設, 2005 (10): 71-73.

[7] 諶潤水. 公路舊橋加固技術與實例[M]. 北京: 人民交通出版社, 2001.

[8] 李友好, 趙豫生. 某病害橋橫向體外預應力加固實踐[J]. 重慶交通學院學報, 2005, 24(2): 18-21.

[9] 沈穎坤, 孫寶俊. 配置帶狀橫向預應力筋的后張預應力板橋研究[J]. 國外橋梁, 2001 (3): 16-21.

[10] 龍馭球, 包世華. 結構力學[M]. 北京: 高等教育出版社, 1996.

[11] 交通部. JTG D60—2004 公路橋涵設計通用規范[S]. 北京: 人民交通出版社, 2004.

責任編輯李思文

AnalysisofUltimateLoadsofaPre-stressedConcreteHollowSlab

GAO Yanyuan1, HONG Tao2, ZHANG Jian3, LIU Hua4

(1.Jiangsu Guangjingxicheng Highway Co., Ltd., Wuxi 214191, China;2.Jiangsu Province Zhenjiang City Engineering Survey and Design Institute, Zhenjiang 212003, China; 3.Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China;4.China Railway Major Bridge (Nanjing) Bridge and Tunnel Inspect and Retrofit Co., Ltd., Nanjing 210031, China)

More and more engineers begin to consider the problem of the ultimate bearing capacity in the process about bridge bearing capacity and damage degree evaluation. Analysis of the ultimate bearing capacity of the bridge is not only used for the limit design, but also for understanding of the destruction of the structure form. The accurate detection of the structure under a given load safety reserve or overload ability can provide the basis for the safe construction and operation management and assurance. A pre-stressed concrete slab was analyzed combined with the curve between load and deformation after the corresponding model was established, and the results can be used for reference in the engineering design.

hollow slab, pre-stress, concrete, ultimate load

TU 312

：A

高巖淵(1970-)，男，本科，高級工程師，主要從事土木工程等方面的研究。

2014-08-18