LDG方法基本思想

王建珍

（長治學院 數學系，山西 長治 046011）

LDG方法基本思想

王建珍

（長治學院 數學系，山西 長治 046011）

文章闡述了一維非線性雙曲問題LDG方法的基本思想，給出單元熵不等式和L2-穩定性的證明，最后給出了基函數的具體求解步驟。

LDG方法；雙曲方程；基函數；穩定性

1 引言

局部不連續伽遼金 （Local discontinuous Galerkin）方法，簡稱LDG方法，是一種間斷有限元方法.

間斷有限元方法最早可以追溯到1973年Reed和Hill關于中子輸運方程的論文[1]，特別是80年代以來，出現了各種各樣的間斷有限元方法.近年來發展的間斷Galerkin有限元方法[2][3][4]，特別是90年代以來，以Cockburn和Chi-Wang Shu為代表提出的Rung-Kutta DG方法[5]，特別引人注目，在許多應用上顯示了前所未有的效能.

間斷有限元方法既保持了有限元方法和FVM的優點，又克服了其不足，特別是易于處理復雜的邊界和邊值問題.同時DG方法具有靈活處理間斷的能力，克服了一般有限元方法不適宜于間斷問題的缺點.DG方法精度的提高可以通過適當選取基函數，即提高單元插值多項式的次數來實現.對于含有高階空間導數的方程，DG方法不能被直接應用，這是因為解空間是由不連續的分段多項式組成.也就是說，近似解僅在時間上是間斷的，在空間中卻不是，空間離散是用連續有限元的標準DG方法.LDG方法卻不同，它是用間斷有限元方法進行空間離散[5]，因而LDG方法也是對DG方法的發展.

首先LDG方法是Cockburn和Shu應用于非定常對流-擴散方程中，后來這個方法又被成功地推廣到一般地含有三階導數的Kdv型方程及含有四階和五階導數的偏微分方程[5]中.

LDG方法的主要思想是將原來帶有高階導數非定常的偏微分方程引進輔助變量重寫成一個一階方程，然后通過RKDG方法進行離散.對于近似解的導數，引進這些局部輔助變量是表面的，在具體問題中很容易被消除.

LDG方法成功的關鍵因素是單元接觸面處的數值流設計，所有數值流設計必須保證數值流的穩定性和局部相容性.

2 一般的一維非線性雙曲問題LDG方法的基本思想：

最簡單的DG方法被設計是為了去解決最簡單的一次雙曲問題.為說明思想，首先研究一般的一維非線性簡單模型：

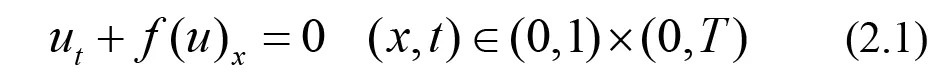
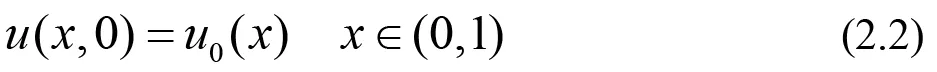
帶有周期邊界條件

我們進行空間離散,對于區間(0,1)任取分割

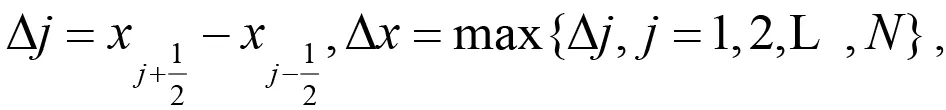
如果我們用任意光滑檢驗函數v(x)乘以 (2,1)和(2,2)，并在Ij上積分，進行簡單的正常分部積分后得到：

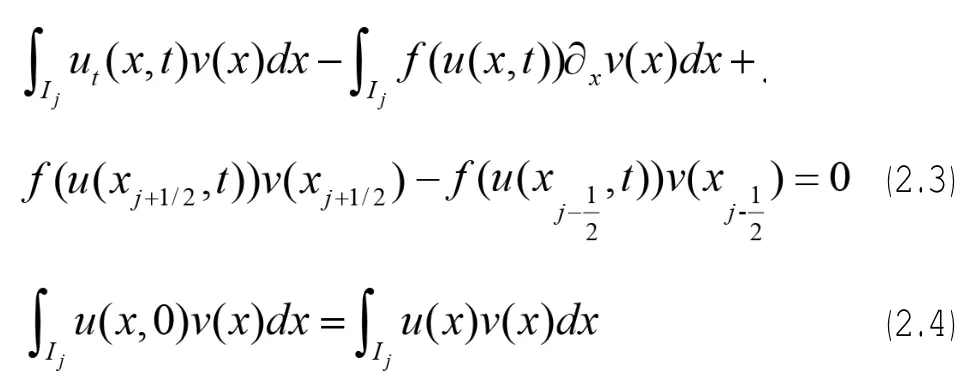
這正是DG方法的起點，接下來，設

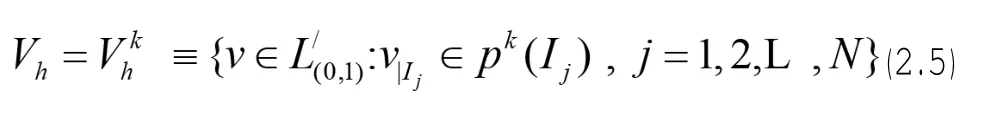
其中，Pk(I)表示I上最多K次多項式空間.我們用最多K次分段多項式uh和vh分別代替解u(x,t)和檢驗函數v(x,t)，即uh,vh∈Vh,當(2.3)中u和v被uh和vh代替時，式中的在點取值的最后兩項中，近似解uh和檢驗函數vh在這些邊界點處是間斷的，將要用一種迎風結構處理這些項.所以在分界點處，uh采用迎風的單值數值流vh在處以IJ內部取值，即：

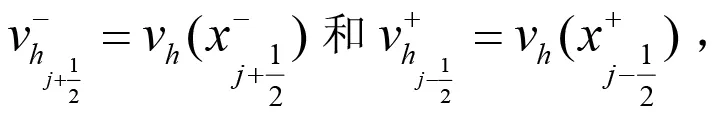
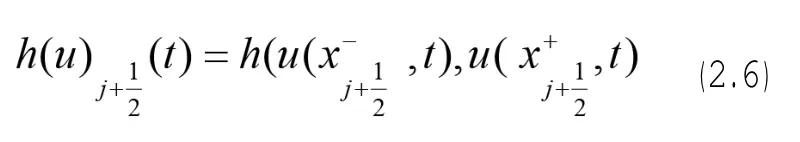
vh在處仍從Ij的內部取值分別為

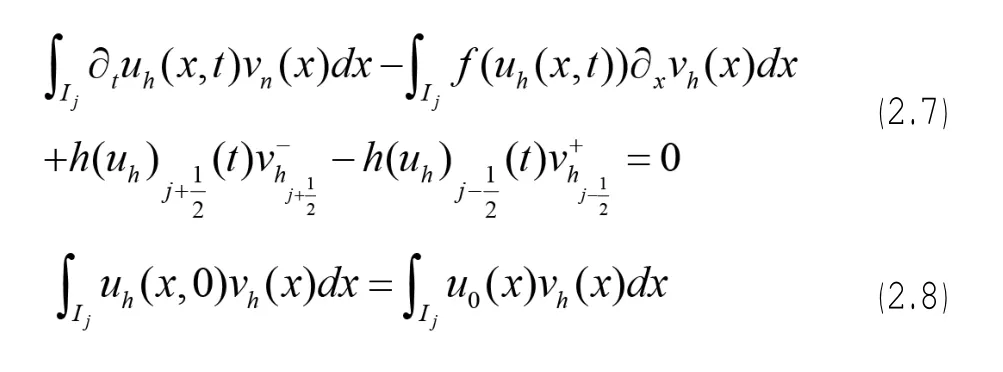
若在(2.7)中取vh為常數，不妨取vh=1，(2.7)變為：

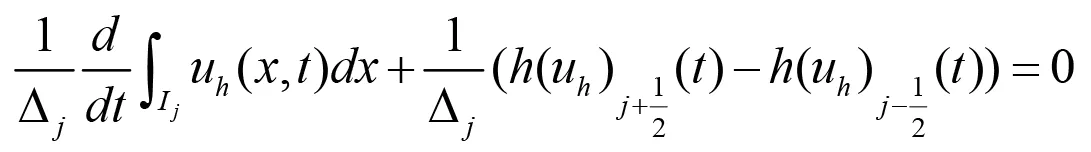
可以看出，當基函數取為常數時，DG方法可還原為有限體積方法，即一階的DG方法相當于一階的有限體積方法.

剩下的工作也僅是數值流h的選擇.首先要求選擇是穩定的，更重要地想要成為所謂的單調格式，從而達到高精度而保持穩定性和收斂性質.

我們從K=0情況入手，也就是uh是分段常數函數時，DG空間離散產生的一種單調格式.

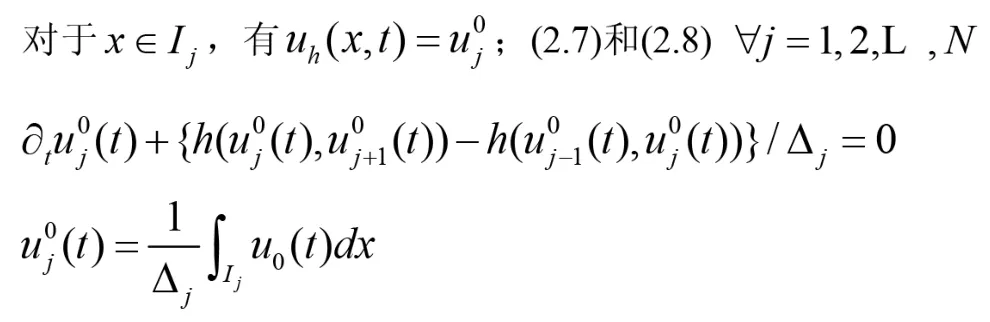
并且要求(2.6)中的h(a,b)滿足：

1o)它是局部滿足Lipschitz連續，并且和f(u)相容，即h(u,u)=f(u)

2o)它對第一個變量是不增函數

3o)它對第二個變量是不減函數

這樣的h(a,b)就定義為一個單調格式.常用的單調格式有：

⑴Godunov流：

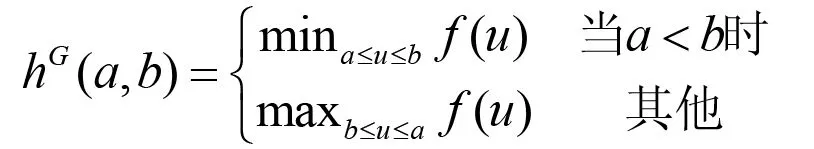
⑵The Engquist-Osher流：

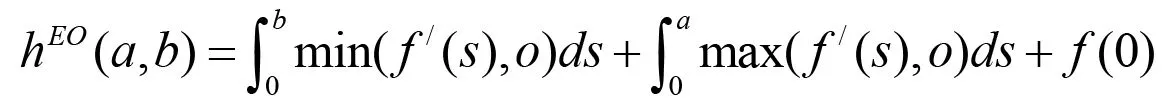
⑶The Lax-Friedrichs流：

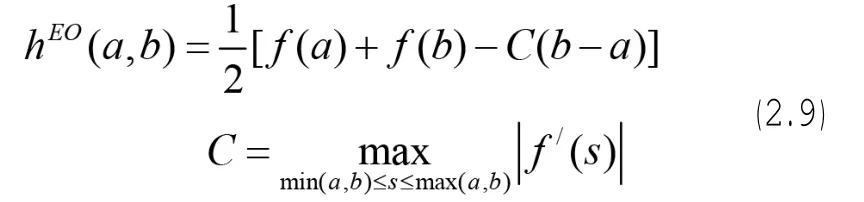
⑷The Local Lax_Friedrichs流：

⑸帶有“熵固定”的Roe流：

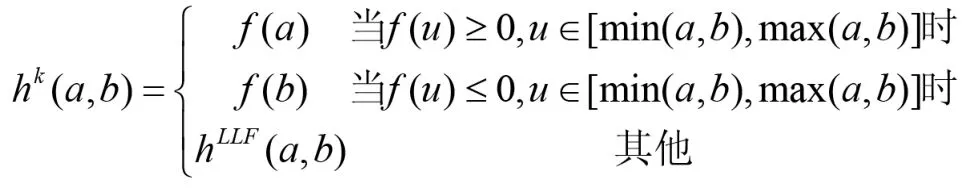
我們能容易使用數值流hG.因為它是產生人工粘性最小的數值流.局部Lax-Friedrichs流比hG流產生更多人工粘性，但他們的性能非常相似.如果f很復雜時，通常用hLF流.然而，數值經驗告訴我們，當逼近的多項式次數K增加時，數值流的選擇不影響逼近的特性.

定理2.1（單元熵不等式）對于數值格式(2.7) -(2.9)，我們有熵不等式:

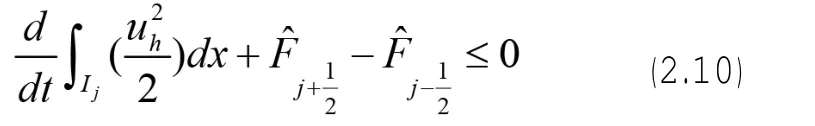
其中

證明：在(2.7)中取vh=uh有

則上式可化為:

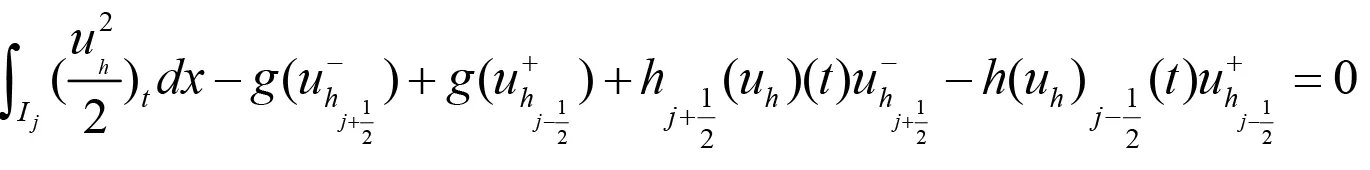
由于

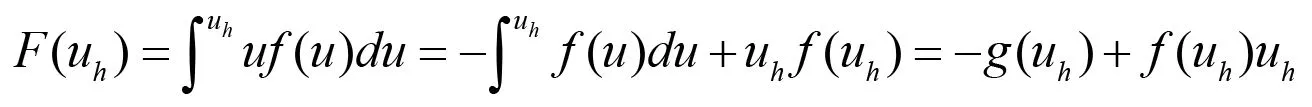
定義

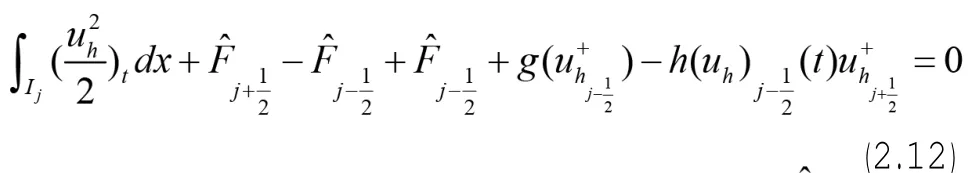
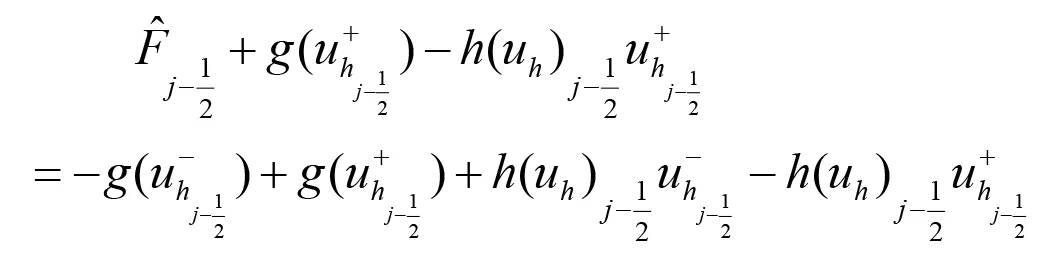
i)如果利用h(a,b)單調性f(↑,↓)，可知

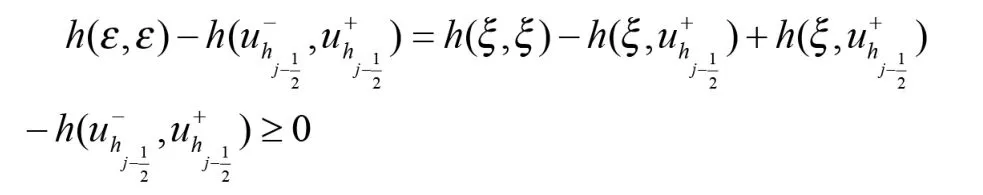
再回到(2.12)就可以得到熵不等式：

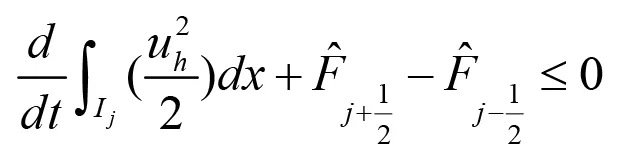
將上式中j=1,2,…N相加，易得L2穩定性.

定理2.2 (L2-穩定性)對于格式(2.7)-(2.9)有,即?T＞0有

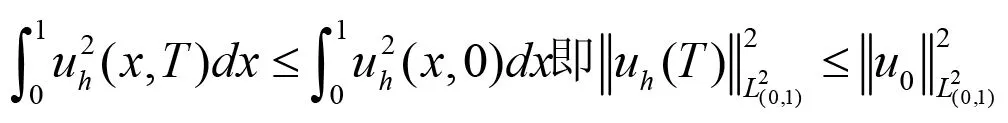
3 基函數及具體求解步驟：

由于Vh中的函數可以出現間斷，不同單元上的基函數可以相互無關，因此需要在每個小IJ上取局部基函數.如果我們選擇Legendre多項式PJ作為局部基函數，可以利用他們的L2正交性，即：

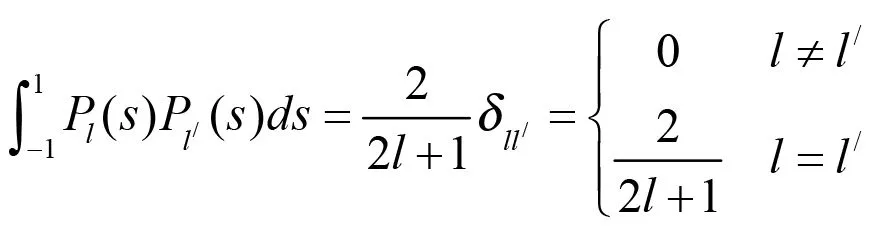
和性質Pl(1)=1,Pl(-1)=(-1)1,進行討論.

令φl(x)=Pl(2(x-xj)/Δj) x∈Ij近似解uh可以表示為

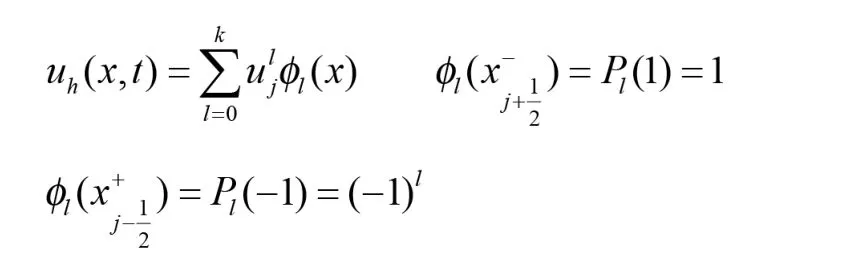
對于弱形式(2.7)和(2.8)，取vh(x)=φl(x);可得下列簡單形式：

?j=1,2,L,N和l=0,L,K

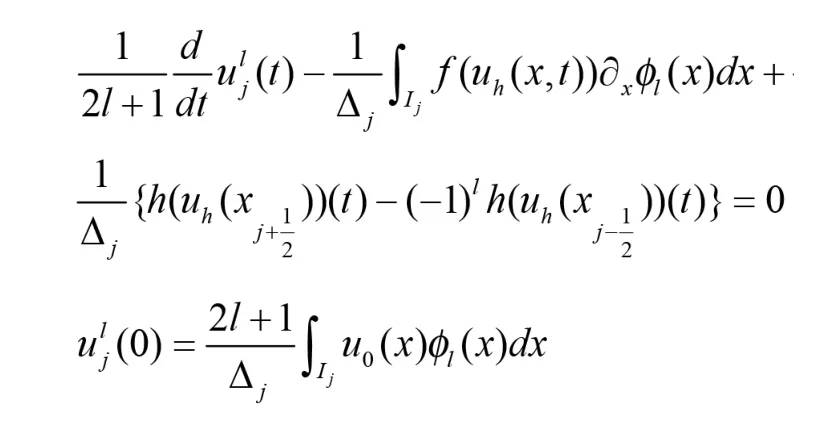
進一步可化為：

是簡單的對角矩陣.

從而，可以給出這種間斷有限元方法的具體計算步驟：

(3)計算

注意：如果我們選擇不同的局部基函數，所形成的質量矩陣能為一個全矩陣，但它永遠是k+1階方陣[6].

以上是對LDG方法的思想、穩定性、線性情況的誤差估計和離散方法進行了分析和討論，對于多維情況可以使用相應的手段進行.

［1］Reed w H and Hill T R.Trangular mesh methods for the Newtron transport equation.［M］LA Report,1973.

［2］Erirsson K,Johnson C and Thomenn V.Time discretization of parabolic problem by the discontinuous Galerkin method.RAIRO.［J］Anal Unmer 1985,（19）:912-928.

［3］Hulme B L.One-step piecewise polynormial Galerkin methods for initial value problems.Math comp,1972,（26）:415-426.

［4］Jamet P.calerkin-type approximation which are discontinuous in time for parabolic equation in a variable domain.［J］SLAM J Numer Anal,1978,（46）:1-26.

［5］CockburnB,HouSandshuC W.TVB Runge-kutta local projection discontinuous Galerkin finite eiement method for scalar conservation laws IV;The multidimensional case.［J］Math comp,1990,（54）:545-581.

［6］劉儒勛，舒其望著.計算流體力學的若干新方法.［M］.北京：科學出版社，2004.160-161.

（責任編輯 趙巨濤）

O241.8

A

1673-2015（2015）02-0004-04

2014—11—23

王建珍（1962—）女，山西太原人，副教授，主要從事高等數學教學與研究。