多線切割機張力控制系統的優化

張桂鵬，李 英，高 志

（華東理工大學 機械與動力工程學院，上海 200237）

0 引言

多線切割技術是一種新型的切割技術，其原理是通過切割線的往復運動，把磨料帶入加工區域進行研磨切割，可一次性將材料加工成幾百上千枚薄片[1]。與傳統的加工技術相比，多線切割機具有生產效率高、加工精度高等優點，在硬脆性材料加工領域有很強的優勢，已逐漸取代傳統的加工技術，成為主流的半導體材料加工裝備[2]。

多線切割機控制系統復雜，影響切割機加工精度的因素有很多，其中切割線張力的控制尤為重要。張力過大，會導致切割線崩斷，造成材料的浪費；張力過小，會導致切割機加工精度降低[3]。控制多線切割機走線系統的張力是關系到生產效率、加工精度的關鍵技術。文獻[4]采用PID積分分離算法對多線切割機的張力進行控制；文獻[5]采用了一種基于相鄰軸誤差的多電機同步控制方法來控制張力波動。目前討論放線輥半徑、走絲換向等擾動因素以及將模糊PID控制方法應用于多線切割機的張力控制等方面的研究還比較少，本文提出了一種基于模糊PID控制的張力控制方法，并對該方法進行了仿真驗證，仿真結果證明了該方法有效地優化了走線系統的張力波動。

1 走線系統運動學與動力學模型

以切割機走線系統的放線端為研究對象來分析張力波動的原因。圖1為放線端結構示意圖，張力控制方式為彈簧張緊。系統裝有角位移傳感器，將測得信號反饋給PLC，形成閉環控制。

1）運動學模型

如圖1所示，張力輪在平衡位置的擺動幅度很小，可以認為張力輪線速度是沿豎直方向的，忽略摩擦力和切割線的彈性伸縮，可以得到張力控制系統的運動學方程。

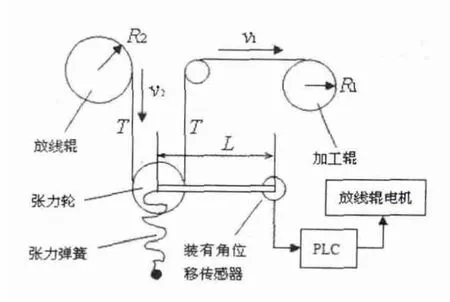
圖1 放線端結構示意圖

根據運動學關系有：

式中：v為張力輪線速度；

v1為放線輥線速度；

v2為加工輥線速度。

張力輪在豎直方向上的位移Δx為線速度的積分：

張力輪的角位移θ為角速度的積分：

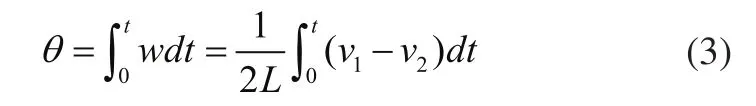
式中：w為張力輪角速度；

L為擺桿長度。

2）動力學模型

如圖1所示，張力輪在平衡位置的擺動幅度很小，可以認為張力輪的運動方向是沿豎直方向的，忽略摩擦力和切割線的彈性伸縮，可以得到張力控制系統的動力學方程：

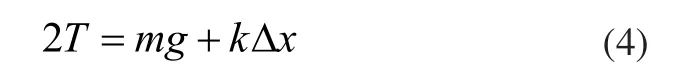
式中：T為切割線張力；

m為張力輪質量；

k為張力彈簧彈性系數。

由此可得切割線的張力表達式為：

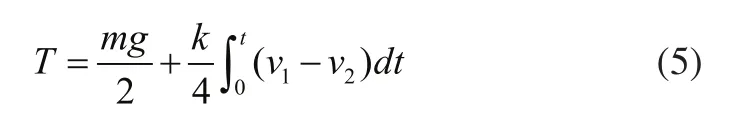
由式(5)可知，系統的張力由兩個部分組成：

第一部分由張力輪的質量決定，當張力輪質量m不變時，該部分為恒定的。

第二部分由加工輥與放線輥的速度同步情況決定，因為張力彈簧的彈性系數k為恒定的。

由式(5)可以得到，控制系統切割線的張力波動是由于放線輥與加工輥速度不同步引起的，兩者速度差越大，張力輪角位移越大，張力波動就越大。

2 控制系統張力擾動因素分析

針對控制系統，首先加入傳統的PID控制方法，以張力輪角位移為輸入，放線輥電機角速度作為輸出，根據上述的運動學與動力學模型，使用Simulink進行建模與仿真并分析控制系統張力擾動因素。以多線切割機的期望線速度作為控制模型的指令輸入，如圖2所示。

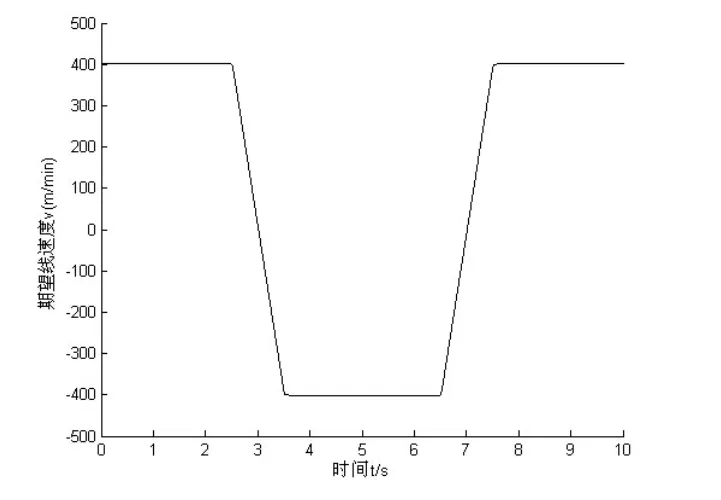
圖2 期望線速度曲線

1）放線輥半徑對控制系統的影響

PID控制器屬于線性控制，即輸入和輸出之間存在線性關系。在本控制系統中，這種線性關系體可以表示為：

式中：A為常數；

w2為放線輥角速度；

對式(6)兩邊同時微分并乘以L：

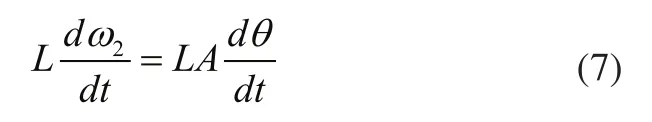
由式(3)可知：

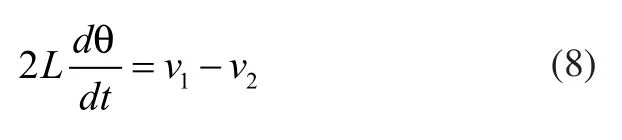
所以有：

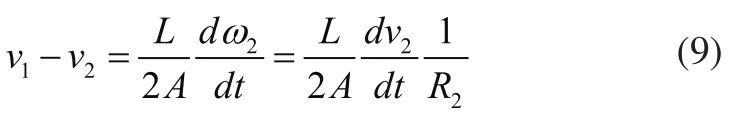
放線輥穩定工作時線速度是恒定的，因此式(9)右邊除了R2項外，其他項均為定值。由此可以得到，放線輥半徑越小，放線輥與加工輥線速度差越大，張力輪角位移越大，張力波動越大。圖3為放線輥半徑R2不同時，系統線速度差的曲線圖，由圖中可以看出前面的分析是正確的。

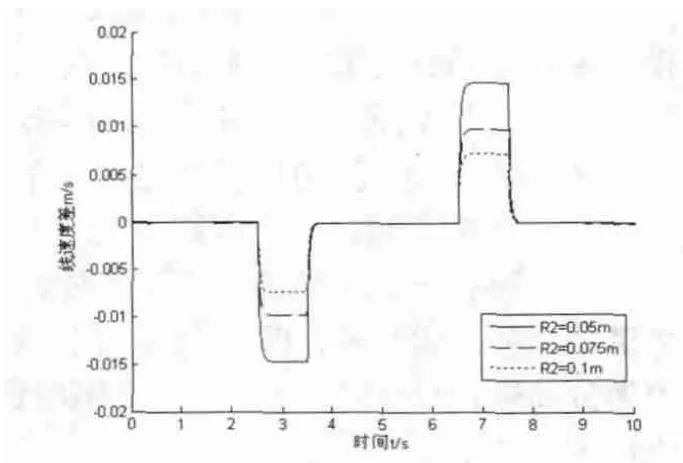
圖3 R2不同時系統線速度差

在多線切割機的實際加工過程中，放線輥半徑R2最小的時刻就是繞在放線輥上的切割線全部放完時，也就是放線輥的半徑。放線輥半徑R2取最小值時，放線輥與加工輥速度差最大，只要此時切割線的張力波動能夠滿足控制要求，那么加工過程中無論R2怎樣變化，均能滿足控制要求。因此在仿真過程中，R2始終選取最小值。

2）走絲換向對系統的影響

在切割機的實際工作過程中，走線速度變化是非常迅速的，走絲換向時間非常短，各電機的速度在短時間內不停地變化，此時會產生明顯的張力波動[6,7]。采用直線變速方式時，切割線在換向時刻會發生瞬時的加速度跳變，導致系統產生很大的張力波動。為了使走絲換向能夠平滑過渡，不發生瞬時的加速度跳變，采用余弦變速來替代直線變速。圖4為直線變速方式下系統張力波動曲線，圖5為余弦變速方式下系統張力波動曲線。

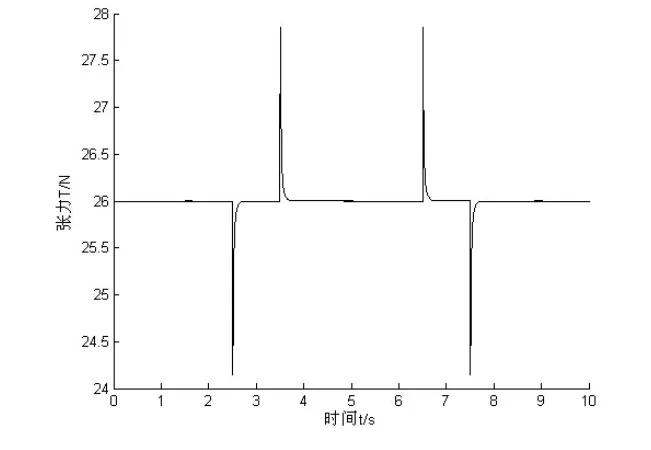
圖4 直線變速方式下系統張力波動曲線

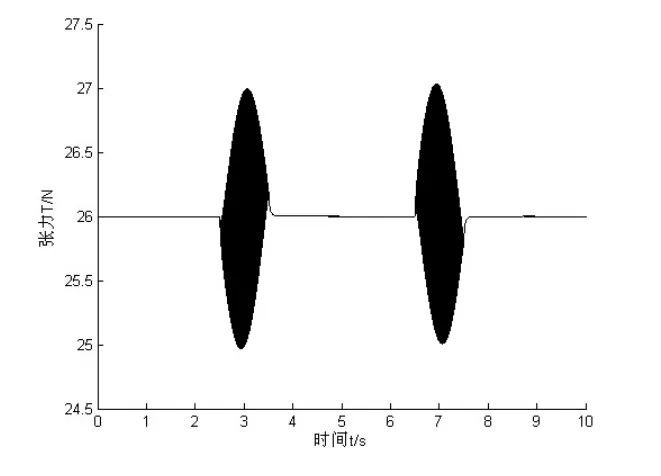
圖5 余弦變速方式下系統張力波動曲線

比較圖4和圖5，可以看出余弦變速方式下切割線張力波動幅度更小，變速過程中的張力變化也更為連續平緩。

3 模糊PID控制器的設計

由圖5可以看出，傳統PID控制方法下的張力波動幅度超過了1N，控制效果并不十分理想。傳統PID控制方法結構簡單、易于控制，但控制精度難以達到預期的控制要求。模糊PID控制方法的精確性、魯棒性以及可靠性等方面均優于傳統PID控制方法，因此設計一個自適應模糊PID控制器，進一步優化張力控制系統[8,9]。

1）控制器的結構設計

模糊控制器采用兩輸入三輸出結構，輸入變量為誤差e與誤差變化率ec，誤差e為張力輪的角位移θ，理想情況下張力輪應處在水平位置，加工過程中產生的任何角位移即為誤差，誤差變化率為dθ/dt。輸出變量為PID參數調整量ΔKp、ΔKi、ΔKd，與PID參數基準量kp、kp、kp相加便得到PID參數Kp、Ki、Kd。

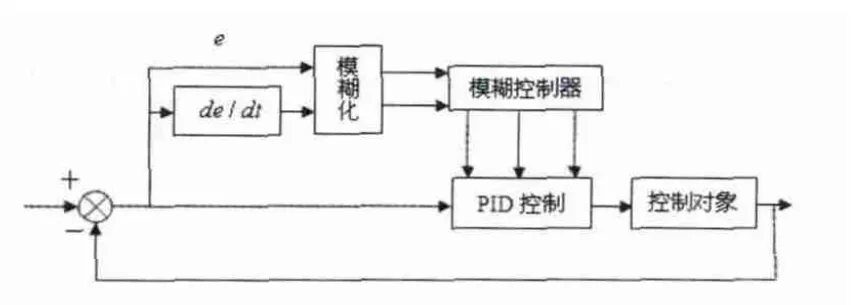
圖6 為模糊PID控制器模型

2）控制器的算法設計

模糊控制器的輸入e、ec，輸出ΔKp、ΔKi、ΔKd的論域為[-5，5]。其模糊子集為{NB，NM，NS，ZO，PS，PM，PB}，各語言變量的意義為NB=負大、NM=負中，NS=負小、ZO=零、PS=正小、PM=正中、PB=正大，各變量均取三角隸屬度函數。

為了保證精度，偏差語言變量E、偏差變化語言變量EC、ΔKp、ΔKi基本論域選定為[-3，3]，ΔKi的基本論域選定為[-0.5，0.5]。得到量化因子Ke=1.667、Kec=1.667，比例因子Kep=0.6、Kei=0.1、Ked=0.6。ΔKp模糊規則表如表1所示，ΔKi、ΔKi模糊規則表略。

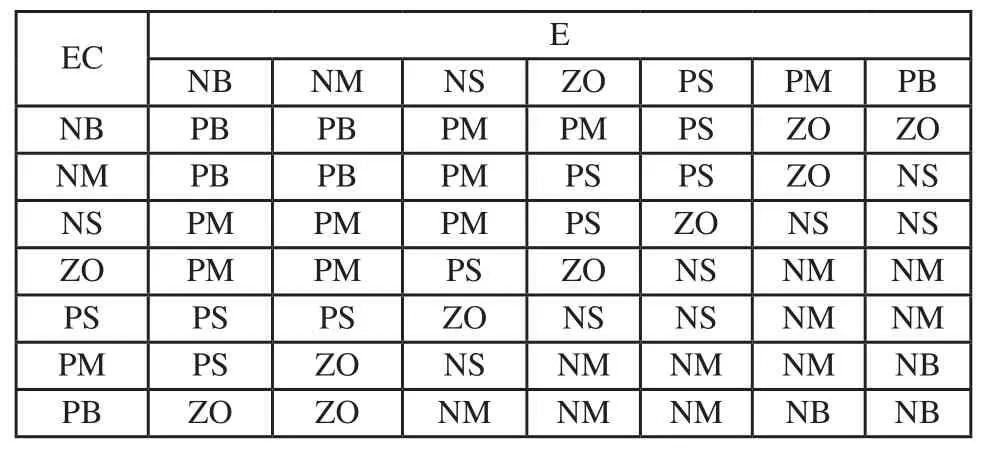
表1 ΔKp模糊規則表

3）仿真結果及分析

切割線線速度如圖2所示，系統走絲換向時間為1s,放線輥半徑為0.075m，采用余弦變速方式，采用模糊PID控制器對系統進行仿真[10]，仿真結果如圖7所示。

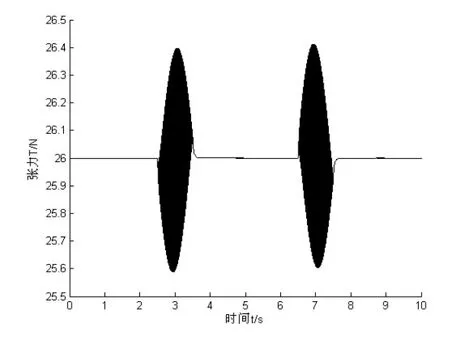
圖7 模糊PID控制張力波動曲線

仿真結果表明：采用模糊PID控制器，系統的張力波動控制在0.4N左右，明顯優于傳統PID控制方法的1N左右，滿足了系統控制精度的要求。

4 結束語

本文建立了走線系統的動力學模型，討論了張力控制的擾動因素并進行了優化，相比于傳統的PID控制方法，采用模糊PID控制方法可以把系統的張力波動控制在允許的范圍內，提高了多線切割機的加工精度。

[1]王琮.半導體材料加工設備的新秀——多線切割機[J].電子工業專用設備,2004,33(4):63-65.

[2]HSU C Y, CHEN C S,TSAO C C.Free abrasive wire saw machining of ceramics[J].The International Journal of Advanced Manufacturing Technology,2009,40(5-6):503-511.

[3]徐旭光,周國安.多線切割晶體表面質量研究[J].電子工業專用設備, 2008,37(11):20-22.

[4]陳學軍,吳鋼華,林海波.基于PID積分分離算法的多線切割機恒張力控制研究[J].組合機床與自動化加工技術,2012,(1):81-84,92.

[5]蔣近,戴瑜興,郜克存,等.多線切割機走線系統的張力控制[J].機械工程學報,2011,47 (5):183-186.

[6]金建華,林海波.數控多線切割機床高精度羅拉軸的關鍵技術研究[J].制造業自動化,2012,34(3):87-91.

[7]黨蘭煥,賀敬良,王學軍,等.多線切割機砂漿控制系統研究[J].制造業自動化,2010,32(6):68-70,231.

[8]宋淑然,阮耀燦,洪添勝,等.果園管道噴霧系統藥液壓力的自整定模糊PID控制[J].農業工程學報,2011,27(6):157-161.

[9]董全成,馮顯英.基于自適應模糊免疫PID的軋花自動控制系統[J].農業工程學報,2013,29(23):30-37.

[10]王中鮮.MATLAB建模與仿真應用[M].機械工業出版社,2010.