多維剖析“探”解法思想指導“究”推廣
——一道高考題的解法探究及推廣歷程

☉甘肅省天水市一中 宮前長

多維剖析“探”解法思想指導“究”推廣
——一道高考題的解法探究及推廣歷程

☉甘肅省天水市一中 宮前長

在學習了《數學》（必修2）（人教A版）“圓與方程”一章后，給學生出了一道高考題，為了教給學生如何進行審題、如何進行解題方法的選擇、思考角度的選擇、數學思想方法的恰當選擇和對試題的拓展，做了一次嘗試，學生的學習積極性高，課堂效果很好.為此，整理此題的審題方法、思考視角選擇及推廣取向，請各位同仁指導！

一、問題提出

題目如圖1，在平面直角坐標系xOy中，已知圓C1：（x+3）2+（y-1）2=4和圓C2：（x-4）2+（y-5）2=4.

（1）若直線l過點A（4，0），且被圓C1截得的弦長為2，求直線l的方程；

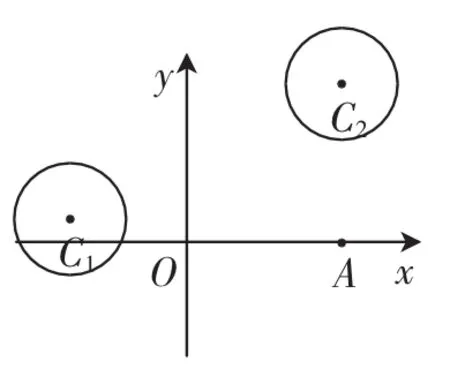
圖1

（2）設P為平面上的點，滿足：存在過點P的無窮多對互相垂直的直線l1和l2，它們分別與圓C1和圓C2相交，且直線l1被圓C1截得的弦長與直線l2被圓C2截得的弦長相等，試求所有滿足條件的點P的坐標.

二、盤點試題特點

試題是立足直線和圓的知識進行問題的設置，題目以考查“能力”為立意的試題.主要考查直線的方程、圓的方程及直線與圓的位置關系，是一道側重于理解與掌握的試題，這些內容在新課標中是屬于“理解、掌握”層次的，從問題的設置上看，試題具有如下的特點：

第（1）問采用具體的數據進行“定量”處理，涉及直線方程、圓的知識（弦、弦心距、半徑和圓的方程等）、垂徑定理、點到直線的距離公式.

第（2）問的設置是采用在定量的基礎上進行“定性”的處理，問題是以“存在性探索問題”的方式給出，自然就會給學生創造出對所涉及的問題進行探究的平臺，由第（1）問的“定量”到第（2）問的“定性”的過渡，對學生能力的考查是螺旋式上升的.

總之，試題的亮點就會“暴露”出來，題目的內涵是以“運動變化的思維”方式進行了“不變”和“變”的相互轉化處理，尤其是“無窮多對”中蘊含了特殊與一般的辯證關系，使所要考查的“直線與圓的位置關系”凸現出來，學生在思考問題時，就會顯露出多層次、多方向、多種思維方式進行考察，從某種意義說，此題是值得進行課堂探究的.

三、探究解題思路與方法

教學中，數學審題的講解很重要，涉及審題思考角度的選擇、數學思想方法的恰當選擇、確定目標條件的選擇、解題操作方法的選擇等，這一些都需要勤觀察、多聯想、對比分析、合理等價表征及大膽的猜想，為解題方案的形成提供了有用的價值.

（1）設直線l的方程為y=k（x-4），即kx-y-4k=0.

由垂徑定理，得圓心C1到直線l的距離d=

（2）通過上述盤點試題特點的分析，就會形成如下幾種解題思路.

思路1：根據試題特點的思路探究，得知所求的點滿足題意的每一對直線與對應圓的圓心的距離是相等的，即直接設出點P的坐標和過此點的直線斜率，根據點到直線的距離公式得到關于點的坐標和斜率的方程，再利用過所求點的直線對是任意的特征解題.

解法1：設點P的坐標為（m，n），直線l1、l2的方程分別

因為直線l1被圓C1截得的弦長與直線l2被圓C2截得的弦長相等，兩圓半徑相等，由垂徑定理，得圓心C1到直線l1與圓心C2到直線l2的距離相等.

思路2：根據試題特點的思路探究，對所求的點滿足題意的每一對直線進行特殊化處理，即此直線對經過圓心，此直線對互相垂直.又其點在兩圓心連線的中垂線上，從而形成如下的解法.

解法2：設點P的坐標為（m，n），兩圓心C1、C2的坐標是（-3，1）、（4，5），設C1C2的中點M的坐標是PC1⊥PC2且過點P、M的直線與直線C1C2垂直，有解得點P的坐標為

思路3：根據試題特點的思路探究，對過所求的點P滿足題意的每一對直線進行特殊化處理，即此直線對互相垂直.又所求點P在兩圓心連線的中垂線上，由等圓的方程相減易知中垂線的方程，從而形成如下的解法.

解法3：設點P的坐標為（m，n），由兩等圓的方程相減可知兩圓心的連線的中垂線的方程是（x+3）2+（y-1）2=（x-4）2+（y-5）2，即14x+8y-31=0.因為點P在中垂線上，所以14m+8n-31=0，與聯立，解得點P的坐標為

思路4：根據試題特點的思路探究，對過所求的點P滿足題意的每一對直線進行特殊化處理，即此直線對經過圓心，此直線對互相垂直，點P恰好是以兩圓心的連線段為正方形的兩個頂點（不含兩圓心），可以借助相應的等腰直角三角形的知識來解決.

解法4：設點P的坐標為（m，n），兩圓心C1、C2的坐標是（-3，1）、（4，5），由兩等圓的方程相減可知兩圓心的連線的中垂線的方程是（x+3）2+（y-1）2=（x-4）2+（y-5）2，即14x+8y-31=0.因為點P在中垂線上，所以14m+8n-31=0.由等腰Rt△PC1C2知，C1C2=√2PC1，即（4+3）2+（5-1）2= 2［（m+3）2+（n-1）2］，聯立上述兩個等式，解得點P的坐標

思路5：根據試題特點的思路探究，對過所求的點P滿足題意的每一對直線對進行特殊化處理，即此直線對經過圓心，此直線對互相垂直，點P恰好是以兩圓心的連線段為直徑的圓與其中垂線的交點，很快聯立方程組得到所求點的坐標.

在進行社區醫院的工作中，對患者進行自我管理模式健康教育是很有必要進行的，社區醫院應該充分認識到這一點，做好對患者的安全教育工作，使其配合醫院的治療，從而增強治療療效，幫助患者恢復身體健康。

解法5：設點P的坐標為（m，n），兩圓心C1、C2的坐標是（-3，1）、（4，5），設C1C2的中點M的坐標是由解法3知兩圓心的連線的中垂線方程是14x+8y-31=0.因為點P在中垂線上，所以14m+8n-31=0.以C1C2為直徑的圓的方程是（x+3）（x-4）+（y-1）（y-5）=0即有（m+3）（m-4）+（n-1）（n-5）=0，聯立上述等式，解關于m、n的方程得點P的坐標為

思路6：由思路4的啟發，所求點P一定組成了特殊的Rt△PC1M（點M是兩圓心連線的中點），直線C1C2旋轉45°后與線段C1C2中垂線的交點是確定的，就是所求的點P，這樣形成一種新的簡單解法.

解法6：兩圓心C1、C2的坐標是（-3，1）、（4，5），設C1C2的中點為M，則由兩等圓的方程相減就得到了線段C1C2中垂線的方程（x+3）2+（y-1）2=（x-4）2+（y-5）2，即14x+8y-31=0.又直線C1C2的斜率是，設過點C1且繞點C1旋轉45°的直線的斜率記為k，由夾角公式得tan45°=1，解得，此時直線C1C2旋轉45°后的直線方程是，聯立兩個方程，解得.從而得點P的坐標

四、結論拓展，合情推廣

通過對試題的分析和解法的探究，就會發現，過所求點的直線對的夾角是直角，也可以改為某一角，但此角的范圍是（0，π），由試題特點的幾何圖形旋轉分析，點是存在的，仍在兩等圓圓心的連線的中垂線上，從而得到下述結論.

結論1：在平面直角坐標系xOy中，已知圓C1：（x-a）2+（y-b）2=r2和圓C2：（x-c）2+（y-d）2=r2.設P為平面上的點，滿足：存在過點P的無窮多對互相垂直的直線l1和l2，它們分別與圓C1和圓C2相交，且直線l1被圓C1截得的弦長與直線l2被圓C2截得的弦長相等，滿足條件的點P一定在兩等圓圓心連線的中垂線上，又在圓心連線為直徑的圓上.

結論2：在平面直角坐標系xOy中，已知圓C1：（x-a）2+（y-b）2=r2和圓C2：（x-c）2+（y-d）2=r2.設P為平面上的點，滿足：存在過點P的無窮多對夾角為α（0＜α＜π）的直線l1和l2，它們分別與圓C1和圓C2相交，且直線l1被圓C1截得的弦長與直線l2被圓C2截得的弦長相等，滿足條件的點P的坐標一定滿足兩等圓的方程相減的直線方程，即滿足兩圓心的連線的中垂線的方程.

由探究解題思路與處理方法中的解法1可知，過某一點的無窮多對互相垂直的直線（割線）被兩個等圓所截的弦長相等，在平面中這樣的點是存在的.如果其他條件不變，只是將兩個“等圓”改為“不是等圓”時，又有怎樣的結果？

推廣：在平面直角坐標系xOy中，已知圓C1：（x-a）2+（y-b）2=和圓C：（x-c）2+（y-d）2=相離.設P為該平面上

2的點，滿足：存在過點P的無窮多對互相垂直的直線l1和l2，它們分別與圓C1和圓C2相交，且直線l1被圓C1截得的弦長與直線l2被圓C2截得的弦長之比為r1∶r2，試求滿足條件的點P的坐標？（解法參照解法1）

五、總結

對一道數學題的問題“點（知識點、關鍵點、連接點、結構點等）”的深入剖析，就會破解它提升難度的“線（知識發展“線”、思維聯系“線”等）”和“面（解析幾何層面、函數層面、向量層面等）”有了更清晰的掌握和理解，為深刻審題和形成解題思路及解法的構思鋪平了道路，也就能夠把握住這道數學題所反映的數學本質，對提升解數學題的能力大有幫助.像本題的“點”主要是“直線對為什么會過定點”、“如何確定直線對過定點”，其“線”和“面”就是“過定點的互相垂直的直線對具備哪些性質”、“過定點的互相垂直的直線對的個數有多少”等，只要解決了這些問題，就會容易形成解題思路與方法.

在平時的數學學習中，多關注對基礎數學問題中所蘊含的思想方法要即時進行歸納、總結，通過對數學問題中的問題“點”進行講命題立意、說題意、探題理、尋方法等“線”和“面”活動，深化思維，自然凸現優美解法，真正回歸到教材中在基礎題上進行挖掘、提煉思想方法，形成高效課堂.

1.羅增儒．數學解題學引論［M］．西安：陜西師范大學出版社，2008.

2.宮前長.關注幾何性質喚出簡捷解法［J］.中學數學（上），2010（10）.

3.宮前長.高考數學復習的根本：回歸教材［J］.中學數學（上），2014（4）.FH