基于緩坡方程在島礁地形上波浪破碎的模擬研究

方亞冰，柳淑學，李金宣，劉思

（大連理工大學海岸和近海工程國家重點實驗室，大連116024）

基于緩坡方程在島礁地形上波浪破碎的模擬研究

方亞冰，柳淑學，李金宣，劉思

（大連理工大學海岸和近海工程國家重點實驗室，大連116024）

波浪從深海傳至近岸島礁時，一般需要經過落差較大的礁坪邊緣，水深急劇變化，導致波浪在傳播過程中發生破碎，因此準確模擬波浪的破碎過程以及破碎后的波高大小，對于島礁海岸工程建設具有重要的意義。緩坡方程是描述近岸波浪傳播變形較好的數值模型之一，文章在采用自適應有限元求解緩坡方程所建立的數值計算模型的基礎上，引入描述波浪破碎的模型，建立可以描述波浪破碎影響的近岸波浪數值模型。基于二維島礁地形上的波浪實驗，比較分析了4種不同的波浪破碎能量損失因子，給出了適合于島礁地形條件下波浪傳播破碎模擬的模型。

二維島礁地形；緩坡方程；波浪破碎

中國海域幅員遼闊、珊瑚島礁眾多，波浪從深海傳至近岸島礁時，一般需經過落差較大的礁坪邊緣。而由于水深的急劇變化，導致與在大多數緩變地形上波浪傳播相比，其規律有所不同。因此建立起能夠模擬波浪在島礁地形上傳播的數值計算模型，對波浪變形進行較為準確的預報是十分有必要的。

考慮到在波浪傳播的過程中，會受到折射、繞射、反射等因素的影響，很多學者在二維橢圓型緩坡方程的基礎上，建立起了多個數值模型（例如：Mei［1］；Tsay and Liu［2］；Chen and Houston［3］；Mattioli［4］），并運用到了實際工程當中。但是，大部分模型都沒有考慮到如島礁地形這種水深差別較大情況下波浪破碎的影響。本文在Berkhoff［5］發展的緩坡方程的基礎上，基于自適應有限元方法來求解緩坡方程［6］，著重考慮波浪破碎因素的影響，針對不同學者提出的4種不同的波浪破碎能量損失因子，對二維島礁地形條件下波浪的傳播進行模擬，通過與實驗結果進行對比、分析，建立起適用于島礁地形下波浪傳播的數值計算模型。

1 數值計算模型

1.1控制方程

考慮到波浪在傳播過程中波浪破碎的效應，有些學者認為可以把波浪破碎作為一項耗散項加入到Berk?hoff的原始緩坡方程當中［7-9］。

式中

其中C（x,y）=ω/k為相速度，Cg(x,y)=為群速度，γ為波浪破碎能量損失因子,可有多種計算模型，將在下文給出。k為波數，與波浪頻率滿足如下色散關系

式中：h為水深。

1.2邊界條件

在近岸波浪傳播模擬過程中，一般需考慮如下邊界條件。

（1）全反射邊界。

（2）部分反射邊界。

式中：α=α1+iα2為復常數，與復反射系數有關，復反射系數可表示為ρ=Reiε；ε為入射波和反射波之間相位差；R為振幅衰減；α與ρ的關系為

（3）入射邊界條件。

對于一般波浪傳播模擬，可認為波浪是從一直線上開始向計算區域內入射傳播的，而在這條直線上有入射勢（ΦI=a）和散射勢ΦS，且不考慮入射邊界對于散射勢的反射，因此有

1.3方程求解

假設將要求解的區域劃分為有限個單元，取其中一個具有代表性的單元，假定權函數為N，采用加權余量法、分部積分和格林公式等，可以建立求解單元上的有限元方程，最后將單元有限元方程在全區域上進行疊加，即可得到如下的有限元方程組

其中[] K具有對稱和稀疏的特點，計算中采用索引存儲法，只儲存上三角的非零元素。方程的求解則采用雙共軛梯度法，模型的建立及具體求解過程參見Liu S X等［6］。

2 波浪破碎能量損失因子的選取及其模擬結果

本文選取了Battjes和Janssen［10］，Dally et al.［11］，Massel［12］，Chawla et al.［13］等建立的4種不同的波浪破碎能量損失因子進行數值計算模擬。這些破碎因子參數都依賴于波高而變化。隨著地形的變化，波高將產生明顯的變化，當波高超過了一定的限制條件，波浪發生破碎，能量發生損失，直到產生適于當地水深條件的波浪。

本文將基于島礁地形波浪傳播的實驗結果，針對上述常用的4種破碎模式進行研究，確定可用于島礁地形條件下波浪破碎模擬的模型。

2.1物理實驗模型

為了模擬島礁地形條件下波浪的傳播特性，劉寧［14］進行了相應的物理模型試驗研究，實驗布置如圖1，水槽長69 m，寬2 m，深1.8 m。實驗將島礁地形簡化為1：5的斜坡，斜坡段水平距離2.5 m，礁坪部分簡化為水平地形，表面為光滑混凝土面，高度0.5 m，水平距離30 m，水槽后端布置斜坡式消能器用于吸收波浪。

模型中布置了18根浪高儀，具體位置及間距詳見圖2。

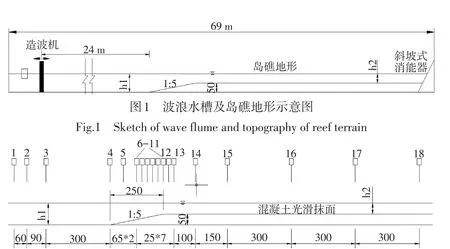
圖2試驗浪高儀布置圖（單位：cm）Fig.2Sketch of wave height gauge

實驗中坡前水深分別為h1=0.625 m、0.715 m和0.835 m，為研究入射波浪大小對于波浪傳播破碎的影響，在特定周期T條件下，逐漸增大入射波浪波高H0進行實驗，具體實驗參數和過程可參考劉寧［14］的論文。

2.2波浪破碎能量損失因子的數值對比分析

2.2.1Battjes和Jassen［10］參數（BJ）

Battjes和Jassen［10］建議波浪破碎能量損失因子可由下式計算

式中：α為可調常數，一般可以取α=1，

在式（13）中，H為當地波高；Hm為最大允許波高，定義如下

式中：γ0為波浪破碎參數。對于淺水，式（14）則可以簡化為Hm=γ0h（γ0取0.8，h表示當地水深）。

事實上，當式（13）中的b=0.3的時候，Qb=1.5×10-5，即Qb→0，γ→0。因此式（13）可以給出破碎波高條件

即當波高H≤Hb時，γ的值等于0（未破碎），否則γ將按照式（11）進行計算。

將式（11）代入式（1）針對上述實驗條件下的波浪傳播進行模擬計算，圖3給出了3種坡前水深條件下、相同周期不同入射大小波浪傳播的模擬結果與物理模擬實驗結果的比較，圖4分別給出了同一水深條件下相同入射波高H0、不同周期波浪傳播的模擬結果與實驗結果的比較，從圖中可以看出：數值模擬給出的波浪破碎點位置與實驗結果基本一致，發生在圖2所示的10～14#浪高儀之間，即距造波邊界距離為30.75～32.5 m；相同水深、相同周期不同入射波高情況下，入射波高越大，波浪破碎后穩定的波高稍小，與實驗結果基本一致；但是相同水深、同一周期不同入射波高情況下，入射波高越大，波浪破碎后的穩定點位置相對于實驗結果前移，而且穩定點之間的距離較大，與實驗結果差別較大，其原因在于式（11）中的Qb是通過迭代求解的，迭代過程甚至達到上千次，迭代過程中會造成破碎后收斂的不一致性，對于落差較大的島礁地形適應性較差。因此，總體來講，雖然該模型可以給出與實驗數據比較一致的結果，但是該方法不是模擬島礁地形條件下破碎波浪的最佳選擇。

2.2.2Dally et al.［11］參數（DDD）

以Horikawa和Kuo［15］的實驗數據為基礎，Dallyet al.［11］建議波浪破碎能量損失因子由下式計算

圖3三種水深下相同周期不同入射波高H0情況下基于BJ破碎因子模型模擬波浪結果與實驗結果的比較Fig.3Comparison of the simulated results based on BJ wave breaking factor and experimental ones for the same periods and different incident wave heightH0under three different depths

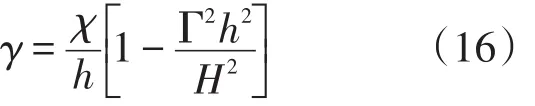
式中：H和h分別為當地波高和水深，參數Γ和χ分別表示穩定波浪因子和波浪延遲因子。劉寧［14］亦根據實驗波浪結果給出了不同情況下的Γ和χ值（表1）,其所得結果與Dally et al.［11］給出相同實驗條件下的結果是一致的，因此采用劉寧［14］所給出的Γ和χ值代入式（16）進行計算。

同樣，式（16）中也包含了一個最低破碎限制條件，即

因此，在實際的計算過程中，如果在之前的迭代過程中所得到的波高H≤Hb，那么γ的值將取0，除此之外γ將按照式（16）進行計算。

與前述類似，圖5給出了采用式（16）所定義的破碎因子，針對3種坡前水深條件下、相同周期不同入射波高波浪傳播的模擬結果與物理模擬實驗結果的比較，而圖6分別給出了同一水深條件下相同入射波高、不同周期波浪傳播的模擬結果與實驗結果的比較。從圖中可以看出：與前述Battjes和Jassen［10］模型模擬結果類似，數值模擬給出的波浪破碎點位置與實驗結果基本一致；相同水深、相同周期不同入射波高情況下，入射波高越大，同樣模擬所得波浪破碎后穩定的波高略微減小，同時，入射波高越大，波浪破碎后的穩定點位置前移，與實驗結果一致。而且，與實驗結果類似，相同水深、相同入射波高但不同周期情況下，波浪破碎后穩定的波高變化不大。因此，綜合不同工況情況下的計算結果，式（16）所定義的波浪破碎因子可以較好地描述島礁地形條件下破碎波浪及波浪傳播過程。

圖4h1=0.715 m水深下入射波高H0=0.14 m不同周期情況下基于BJ破碎因子模型模擬波浪結果與實驗結果的比較Fig.4Comparison of the simulated results based on BJ wave breaking factor and experimental ones for the incident wave heightH0=0.14 mand different periods under the depthh1=0.715 m

表1不同水深比下規則波試驗所得Γ和χ參數取值Tab.1TheΓandχvalues for regular waves with different ε

圖5三種水深下相同周期不同入射波高H0情況下基于DDD破碎因子模型模擬波浪結果與實驗結果的比較Fig.5Comparison of the simulated results based on DDD wave breaking factor and experimental ones for the same periods and different incident wave heightH0under three different depths

2.2.3Massel［12］的參數（SD）

Massel［12］給出波浪破碎能量損失因子的計算模式為

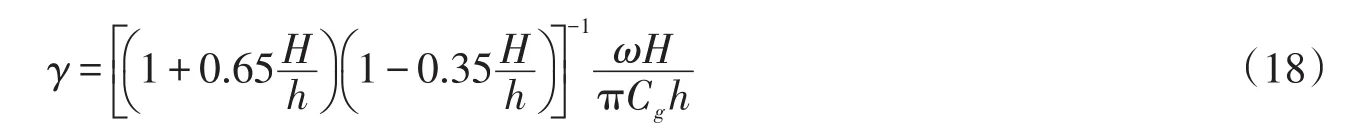
但是在實際計算過程中，發現當H＞2.85h的時候，γ＜0，因此在計算γ時，當地波高H應包含一個最高限制條件，即

另一方面，在數值計算過程中，同樣發現當波浪發生破碎后，波高會隨著波浪的傳播，逐漸遞減至0，這不符合實際波浪的傳播情況，其原因是，不同于前述2種破碎波浪因子，式（18）未給出最低限制條件，導致該式不能給出有效的結果，因此為了更好地模擬實際波浪傳播，仍取式（17）作為采用式（18）進行波浪模擬時的限制條件。

與上述結果類似，圖7和圖8分別給出了采用式（18）所定義的波浪破碎因子數值模擬的結果與實驗結果的對比，從圖中可以看出，采用該模型數值模擬所得波浪破碎點所在位置普遍比實驗結果前移，即波浪較實驗波浪提前破碎，但破碎波高大致相同；而在相同水深、相同周期和不同入射波高情況下，入射波高越大，波浪破碎后模擬所得穩定的波高比實驗結果偏大，同時入射波高增大時，波浪破碎后的穩定點位置沒有明顯的前移，甚至還有退后的趨勢，與實驗結果差別較大。另外，相同水深、相同入射波高不同周期情況下，隨著周期的減小，波浪破碎后穩定的波高增大，且增大幅度比較大，與實驗結果差別也較大。這說明式（18）描述的破碎因子不能較好地模擬島礁地形條件下波浪破碎的情況。

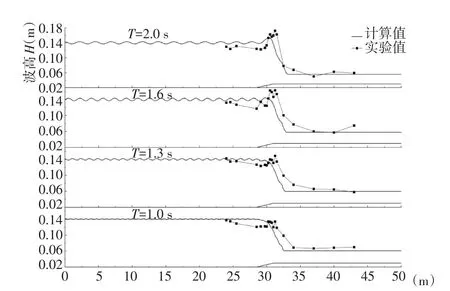
圖6h1=0.715 m水深下入射波高H0=0.14 m不同周期情況下基于DDD破碎因子模型模擬波浪結果與實驗結果的比較Fig.6Comparison of the simulated results based on DDD wave breaking factor and experimental ones for the incident wave heightH0=0.14 mand different periods under the depthh1=0.715 m

圖7三種水深下同周期不同入射波高H0情況下基于SD破碎因子模型模擬波浪結果與實驗結果的比較Fig.7Comparison of the simulated results based on SD wave breaking factor and experimental ones for the same periods and different incident wave heightH0under three different depths

2.2.4Chawla et al.［13］的參數（COK）

Chawla et al.［13］依據Thornton和Guza［16］所統計的波浪破碎數據，結合基于方程（1）式的橢圓形近似模型，歸納推導出了下面的破碎因子計算公式：

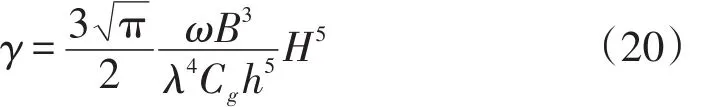
式中:λ和B建議分別取1.0和0.6。該式與式（18）類似，缺少一個限制條件（即γ=0時Hb的取值），導致波高出現不合理的結果，所以仍然采取式（17）作為相應的限制條件。

同樣，圖9和圖10分別給出了數值計算結果與實驗結果的比較，從圖中可以看出：受所引入的破碎因子影響，波浪破碎之前的波高波動比上述模型（BJ、DDD、SD）給出的結果大，而且波浪破碎點的位置與實驗結果亦有很大的差別，而且隨入射波高增大，數值計算所得波浪破碎后的穩定波高稍小于實驗結果，而且波浪破碎后的穩定點位置前移，幅度較大，與實驗結果差別較大。因此，式（20）也不能較好地描述島礁地形條件下波浪的傳播情況。

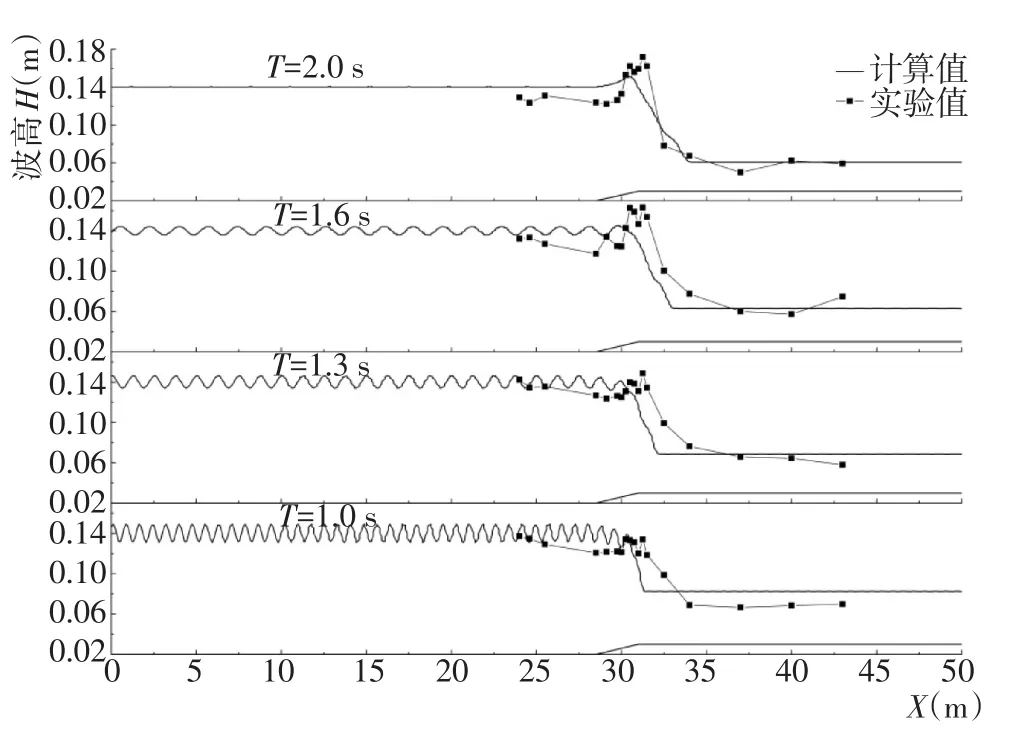
圖8h1=0.715 m水深下入射波高H0=0.14 m不同周期情況下基于SD破碎因子模型模擬波浪結果與實驗結果的比較Fig.8Comparison of the simulated results based on SD wave breaking factor and experimental ones for the incident wave heightH0=0.14 m and different periods under the depthh1=0.715 m

2.2.5波浪破碎能量損失因子的對比

為進一步清楚的比較上述4種波浪破碎能量損失因子對島礁地形條件下波浪傳播的適應性，圖11給出了這4種波浪破碎能量損失因子在3種坡前水深條件下、相同周期、相同入射大小波浪傳播的模擬結果的比較。由圖可以看出，如前所述，BJ破碎因子模擬波浪破碎后穩定點的位置偏后，且穩定波高明顯偏高；COK破碎因子雖然模擬所得穩定波高與試驗結果差別不大，但是亦存在波浪破碎后穩定點位置偏后的問題；SD破碎因子有時波浪破碎后模擬所得穩定波高偏大；綜合比較，DDD破碎因子各方面模擬結果均與實驗結果一致，可以較好地描述島礁地形條件下的破碎波浪。

圖9三種水深下同周期不同入射波高H0情況下基于COK破碎因子模型模擬波浪結果與實驗結果的比較Fig.9Comparison of the simulated results based on COK wave breaking factor and experimental ones for the same periods and different incident wave heightH0under three different depths

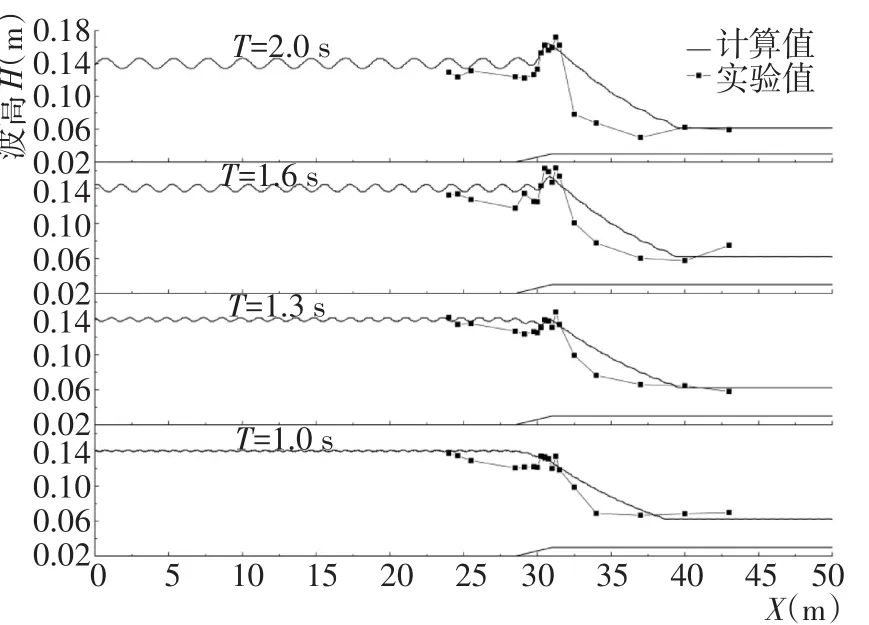
圖10h1=0.715 m水深下入射波高H0=0.14 m入射波高不同周期情況下基于COK破碎因子模型模擬波浪結果與實驗結果的比較Fig.10Comparison of the simulated results based on COK wave breaking factor and experimental ones for the incident wave heightH0=0.14 mand different periods under the depthh1=0.715 m

圖11三種水深下同周期同入射波高H0情況下四種破碎因子的比較Fig.11Comparison of the four wave breaking factors for the same periods and incident wave heightH0under three different depths

3 結語

波浪在向島礁傳播時，水深急劇變化，與其他緩變地形上的波浪傳播運動不同。準確地模擬島礁地形條件下波浪的破碎，對于島礁地形上波浪傳播的模擬具有重要的意義，本文在采用自適應有限元方法來求解緩坡方程的基礎上，著重考慮波浪破碎因子對于波浪傳播模擬結果的影響，建立起基于緩坡方程適用于求解島礁地形下波浪傳播的數值計算模型。

本文選用了Battjes和Janssen［10］，Dally et al.［11］，Massel［12］，Chawla et al.［13］等人提出的不同的波浪破碎能量損失因子分別建立數值計算模型，針對二維島礁地形條件下波浪的傳播進行模擬。為了考慮入射波高大小對于波浪破碎的影響，在模擬過程中，逐漸增大入射波高，對于波浪的傳播進行計算。通過計算結果與實驗結果進行對比分析，綜合考慮波浪破碎點的位置和波高、波浪破碎后穩定點的位置以及穩定后的波高大小等因素，對比分析結果表明，由Dally et al.［11］建議的式（16）作為描述波浪破碎能量損失因子，結合通用的緩坡方程所建立的數值計算模型可以較好地描述典型島礁地形條件下波浪的傳播計算。

參考文獻：

［1］Mei C C.The Applied Dynamics of Ocean Surface Waves［M］.New York:Wiley,1983.

［2］Tsay T K,Liu P L F.A finite element model for wave refraction and diffraction［J］.Applied Ocean Research,1983,5（1）:30-37.

［3］Chen H S,Houston J R.Calculation of Water Oscillations in Coastal Harbors;HARBS and HARBD User′s Manual［R］.Vicks?burg MS:Coastal Engineering Research Center,1987.

［4］Mattioli F.Dynamic response of the Lido channel to wavemotion in the presence of movable barriers［J］.IlNuovoCimento C,1996, 19（1）:177-194.

［5］Berkhoff J C W.Mathematical models for simple harmonic liner water waves?wave diffraction and refraction［R］.Delft,the Nether?lands:Delft Hydraulic Lab.,1976.

［6］LIU S X,SUN B,SUN Z B,et al.Self?adaptive FEM numerical modelling of the mild?slope equation［J］.Applied Mathematical Modelling,2008,32:2 775-2 791.

［7］Liuzhi Zhao,Vijay Panchang,Chen W,et al.Simulation of wave breaking effects in two?dimensional elliptic harbor wave models［J］.Coastal Engineering,2001,42:359-373.

［8］唐軍,沈永明,鄭永紅，等.結合橢圓型緩坡方程模擬近岸波流場［J］.海洋學報,2006,28（1）:146-151. TANG J,SHEN Y M,ZHENG Y H,et al.The numerical simulation of nearshore current combined with the elliptic mild?slope equation［J］.Acta Oceanologica Sinica,2006,28（1）:146-151.

［9］祁峰,曹宏生.應用改進的橢圓型緩坡方程數值模擬波浪傳播變形［C］//中國海洋工程學會.第十三屆中國海洋（岸）工程學術討論會論文集.北京：海洋出版社，2007:316-318.

［10］Battjes J A,Janssen J.Energy loss and set?up due to breaking of random waves［J］.Coastal Engineering Proceedings,1978,1（16）:569-587.

［11］Dally W R,Dean R G,Dalrymple R A.Wave height variation across beaches of arbitrary profile［J］.Journal of Geophysical Re?search:Oceans（1978-2012）,1985,90（C6）:11 917-11 927.

［12］Massel S R.Inclusion of wave?breaking mechanism in a modified mild?slope model［M］//Banner M L,Grimshaw R H J.Breaking Waves.Springer?Verlag Berlin and Heidelberg GmbH&Co.K,1992:319-324.

［13］Chawla A,?zkan?Haller H T,Kirby J T.Spectral model for wave transformation and breaking over irregular bathymetry［J］.Jour?nal of waterway,port,coastal,and ocean engineering,1998,124（4）:189-198.

［14］劉寧.波浪在島礁地形上傳播特性的試驗研究［D］.大連:大連理工大學,2014.

［15］Horikawa K,Kuo C T.A study on wave transformation inside surf zone［J］.Coastal Engineering Proceedings,1966,1（10）:217-233.

［16］Thornton E B,Guza R T.Transformation of wave height distribution［J］.J.Geophys.Res,1983,88（10）:5 925-5 938.

Simulation of wave breaking on the reefs terrain using mild?slope equation

FANG Ya?bing,LIU Shu?xue,LI Jin?xuan,LIU Si
（State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China）

When the waves propagate from the deep water to the inshore reefs,a large gap reef flat must be overcome,leading to dramatic changes in water depth.This will cause the wave breaking.It is important for the engi?neering design on the terrain to accurately simulate the wave breaking and calculate the wave heights after wave breaking.Mild?slope equation is one of the best numerical models to describe near shore wave transformation. Based on a self?adaptive finite element numerical model to solve the mild?slope equation,a near shore numerical model to simulate wave breaking was developed by introducing the wave breaking model in this paper.Four kinds of wave breaking model were used and compared based on the experimental results of the wave propagation on the two?dimensional reefs terrain.A numerical model for solving the wave transformation on the two?dimensional reefs ter?rain was proposed.

two?dimensional reefs terrain;mild?slope equation;wave breaking

TV142；TV131.6

A

1005-8443（2015）04-0290-07

2014-12-05；

2015-01-04

國家重點基礎研究發展（973）計劃資助項目（2013CB036101，2011CB013703）；國家自然科學基金創新研究群體基金（51221961）

方亞冰（1989-），男，湖南省郴州市桂東縣人，碩士研究生，主要從事近岸波浪傳播特性的模擬研究。

Biography：FANG Ya?bing(1989-),male,master student.