山谷地形橋梁橫向地震反應特性分析

張少為 葉愛君

(同濟大學橋梁工程系，上海200092)

1 引言

山谷地形橋梁中間橋墩高，邊上橋墩矮，相鄰聯橋梁的剛度差異較大，動力特性差異也較大，容易產生非同向振動，因此地震反應與常規橋梁相比更為復雜，對抗震不利。對此，我國的《城市橋梁抗震設計規范》[1]規定梁式橋(多聯橋)相鄰聯的基本周期比宜大于等于0.7(含順橋向和橫橋向)，從而減小相鄰聯間的非同向振動。

目前，關于山谷地形橋梁的抗震研究主要集中在縱橋向。文獻[2]的結論為:山谷非規則橋梁相鄰聯的縱向基本周期相差較大，縱向地震輸入下，會導致伸縮縫相鄰聯非同向振動，引起伸縮縫處相鄰聯產生較大的相對位移和伸縮縫處的碰撞。文獻[3]針對簡支梁橋的研究表明，當鄰跨的剛度相差較大時，即結構動力特性差異較大時，鄰跨剛度比對結構地震反應的影響更為顯著。在縱向地震作用下，主梁發生縱向平動，因此可以忽略主梁剛度的影響，僅需考慮橋墩剛度對地震反應的影響。但是，在橫橋向地震作用下，主梁的橫向振動不可忽略，而主梁的橫向振動又會受到橋墩的約束，因此，主梁的剛度、橋墩的剛度都會影響橋梁的橫向地震反應。目前對于橋梁橫向地震反應的研究很少研究主梁剛度的影響，一般認為上部結構產生的橫向地震慣性力按橋墩剛度分配給各橋墩[4-6]。而對于山谷地形橋梁來說，橋墩的剛度變化很大，因而墩梁相對剛度在各聯間的差別很大。另外，實際工程中，主梁橫向剛度的不同主要是設計時橋寬或者梁高的不同引起的，而主梁質量占全橋總質量的比重很大，于是主梁剛度改變所附帶的質量變化也是一個不容忽視的影響因素。因此，山谷地形橋梁的橫向地震反應具有與縱橋向完全不同的特點，涉及地震慣性力在各墩間的分配以及相鄰聯的橫向動力耦聯性問題，非常復雜，目前還缺乏相關的研究。

為此，本文建立了典型山谷地形橋梁的三維動力計算模型，同時考慮主梁和橋墩剛度的影響，從動力特性出發，分析該類橋梁的橫向地震慣性力分配特點以及相鄰聯橋梁之間的耦聯性，從而揭示山谷地形橋梁的橫向地震反應特性。

2 動力計算模型及地震動輸入

本文以實際橋梁工程為背景，建立了不同主墩墩高的三個典型山谷地形橋梁的動力計算模型，采用規范反應譜作為地震輸入，分析山谷地形橋梁的橫向地震反應。

2.1 動力模型

本文建立的三個計算模型如圖1所示。全橋共三聯，左右兩個邊聯即左右引橋對稱(以下都稱為引橋)，各為三跨連續梁橋，墩高變化劇烈;中間聯即主橋為四跨連續剛構(以下都稱為主橋)，所有橋墩等高，三個模型的主橋墩高分別為30 m、60 m、90 m。各墩底皆采用全約束，主橋剛構部分墩梁固結，其余各墩與主梁的約束條件見表1。

對于主梁剛度，本文假定主梁剛度不同是由橋寬變化引起的，因此通過將橋寬改為原來的n倍來改變主梁剛度，則主梁橫橋向剛度變為原來的n3倍，而主梁質量變為原來的n倍。原橋寬12 m，本文考慮了1倍橋寬、1.58倍橋寬和2倍橋寬三種情況來研究，對應剛度為1倍主梁剛度、4倍主梁剛度和8倍主梁剛度。

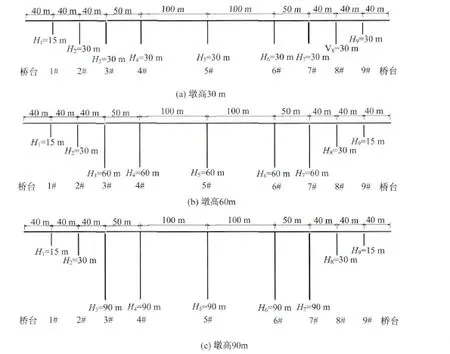
圖1 計算模型Fig.1 Calculation models

2.2 地震動輸入

本文采用規范[5]反應譜作為地震輸入，地震動峰值加速度0.1 g，特征周期0.45 s，場地調整系數取1.0，阻尼調整系數取1.0，重要性系數取0.5，如圖2 所示。

3 山谷地形橋梁的橫向動力特性

圖3顯示了山谷地形橋梁的橫向基本振型，由其振型特點可以看出墩、梁剛度對基本周期都存在一定影響。

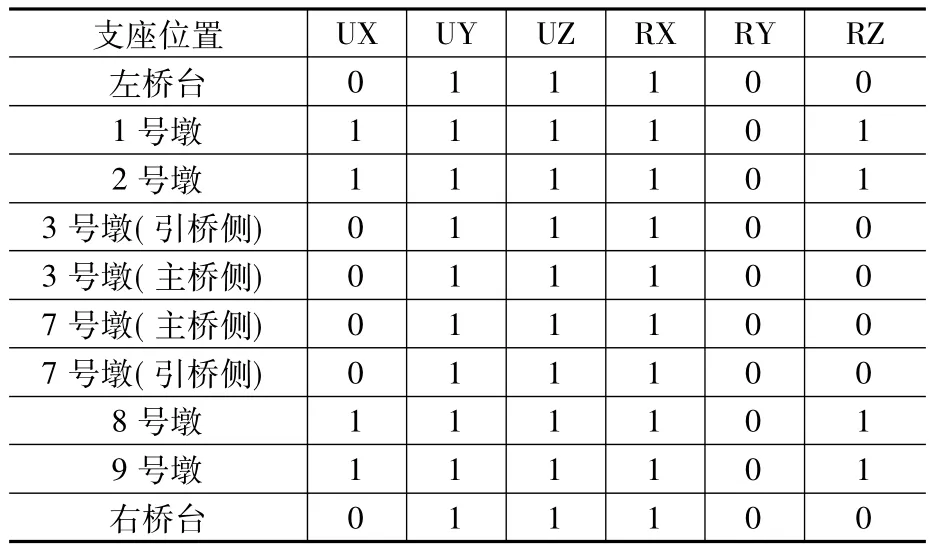
表1 墩梁約束條件Table 1 Constraint conditions

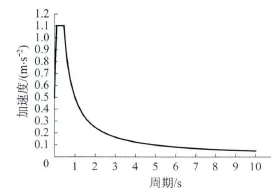
圖2 加速度反應譜Fig.2 Acceleration response spectrum curves

圖3 山谷地形橋梁橫向基本振型Fig.3 Transverse fundamental mode of valley bridg

本文考慮了墩高30 m、60 m、90 m三種情況，而對于主梁剛度，本文考慮了1倍、4倍、8倍三種情況，表2給出了各種情況的基本周期。

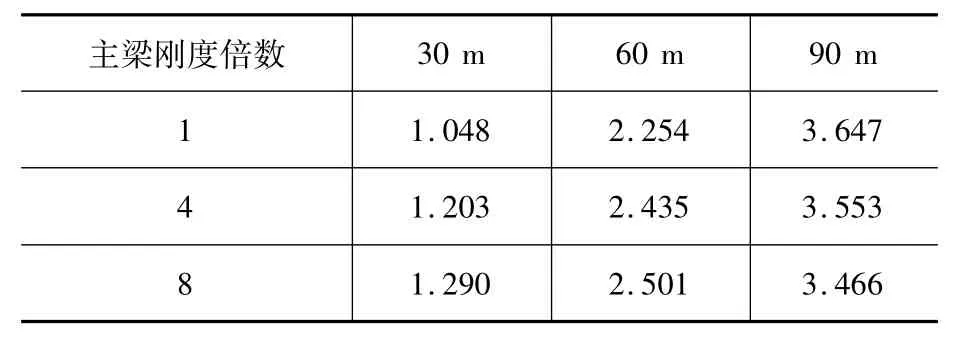
表2 不同情況各橋基本周期Table 2 Fundamental period in different cases s

由表2可知，隨主梁剛度倍數的增加，墩高30 m和60 m時，基本周期增大，而墩高90 m時，基本周期減小。主梁剛度變化即橋寬變化會同時影響橋梁總體剛度和總體質量，而橋梁總體剛度和總體質量變化幅度的相對大小則會直接影響到橋梁的基本周期。當墩高30 m時，墩高較矮，橋墩剛度較大，主梁質量占結構總質量的比重較大，而主梁剛度占結構總剛度的比重相對較小。主梁剛度變化即橋寬變化后，橋梁總質量變化幅度較大，而總剛度變化幅度較小，所以此時橋梁基本周期總體會增大。當墩高為60 m和90 m時，情況則相反。墩高較高，橋墩剛度較小，主梁質量占結構總質量的比重相對不大，而主梁剛度占結構總剛度的比重相對較大。主梁剛度變化即橋寬變化后，橋梁總質量變化幅度較小，橋梁總剛度變化幅度較大，所以此時橋梁基本周期總體會減小。

4 橋梁橫向地震反應特性分析

4.1 地震慣性力分配規律

橋墩彎矩除了受到慣性力大小控制外同時還受到墩高的控制，沒有辦法清晰地表現出慣性力的分配規律。因此本文采用墩頂剪力來對慣性力的分配進行分析。

圖4給出了各墩頂的地震剪力包絡圖。

由圖4可知，對于主橋，各墩墩高相等，中間橋墩的橫向位移大于兩側橋墩，因此墩頂剪力從中間向兩側逐漸減小。對于引橋，墩高變化劇烈，因此隨著墩高的降低，墩頂剪力增加。

隨著主梁剛度的增加，各墩墩頂剪力都有不同程度的增加且慣性力分配的趨勢都相同。當墩高30 m時，引橋的增加幅度較小，主橋的增加幅度較大。當墩高90 m時，引橋的增加幅度較大，主橋的增加幅度較小。易見墩高60 m時的情況是墩高30 m和墩高90 m間的中間狀態，所以下面著重分析墩高30 m和墩高90 m的情況。

結合圖4和表2可知，對于墩高30 m，隨著主梁剛度增加即橋寬增加，橋梁基本周期增大，加速度減小，但是此時反應譜處于平緩段，加速度減小幅度較小。相對的，主梁質量翻倍，結構總質量增加幅度較大，所以墩頂慣性力總體仍是增大的。而墩高90 m時，橋梁基本周期減小，加速度和主梁質量都增加，所以墩頂慣性力增大。

4.2 地震橫向位移

圖5給出了主梁的地震橫向位移包絡圖。由圖5可知，墩高30 m時，隨著主梁剛度的增加，主梁橫向位移增加。墩高90 m時，隨著主梁剛度的增加，主梁橫向位移減小。而墩高60 m時是墩高30 m和90 m的中間狀態。

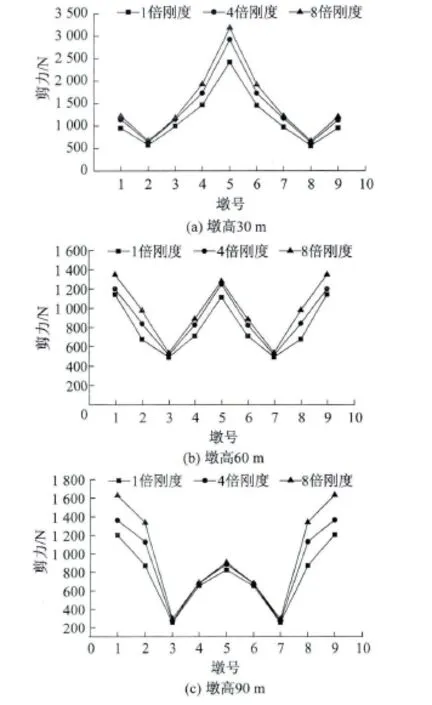
圖4 地震墩頂剪力包絡圖Fig.4 Top shear envelope diagram

對于墩高30 m，結合表2，隨著主梁剛度的增加基本周期增大，所以位移也增加。對于墩高90 m，隨著主梁剛度的增加基本周期減小，所以位移也減小。

同時由圖5可見，隨著墩高的增加，橫向位移包絡圖越來越趨于平滑，這是因為橋墩剛度減小，對于主梁的約束作用也隨之減弱。

4.3 相鄰聯的地震耦聯性

山谷地形橋梁相鄰聯剛度相差較大，主梁剛度的改變會影響慣性力的傳遞。因此本文研究了不同墩高情況下，主梁剛度變化對于相鄰聯內力耦聯性的影響。本文分別建立了三個單聯模型，即左引橋單聯模型(左橋臺、1#—3#墩)，主橋單聯模型(3#—7#墩)，和右引橋單聯模型(7#—9#墩、右橋臺)。分別將主橋和左右引橋單獨一聯情況下的各墩墩頂剪力與主橋和引橋相連后的各墩墩頂剪力進行比較后，可以得到耦聯性對各墩地震慣性力的影響。圖6為單聯墩頂剪力與相連后的三聯墩頂剪力的比值情況。

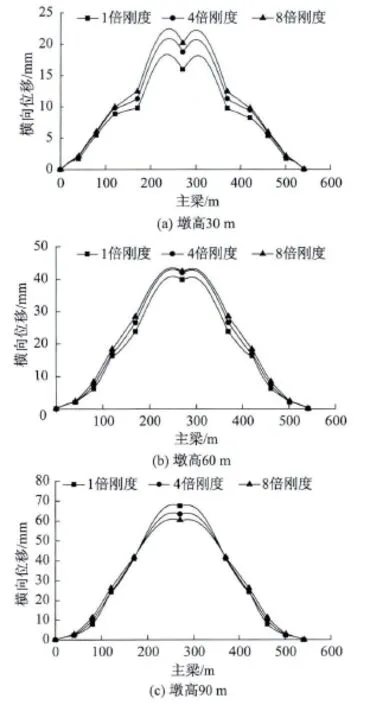
圖5 主梁地震橫向位移包絡圖Fig.5 Transverse displacment envelope diagram

根據圖6，墩高30 m時，相鄰聯相連后主橋剪力增大，引橋剪力減小;墩高90 m時，相鄰聯相連后主橋剪力減小，引橋剪力也減小。墩高60 m為二者的中間狀態。總體來說，主橋的中間橋墩即4號、5號、6號橋墩受主、引橋耦聯性的影響不大，但引橋受耦聯性的影響較大，而過渡墩受耦聯性的影響很大。考慮主橋的影響后，引橋各墩分擔的慣性力會減小，隨著主橋墩高的減小，慣性力減小的幅度增大。考慮耦聯性后，過渡墩的剪力相對比較接近較剛的引橋模型中的結果，而較柔的主橋模型的計算結果誤差較大。

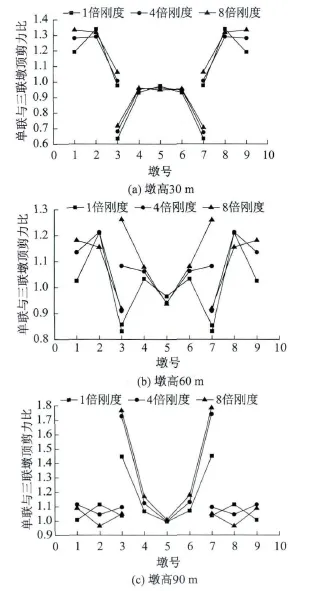
圖6 地震墩頂剪力比Fig.6 Top shear ratios

另外，圖6還表明，主梁剛度對相鄰聯地震耦聯性的影響很大，而且耦聯性越強，主梁剛度的影響也越大，但影響規律復雜，還與橋墩剛度的變化有關。比如，對于受耦聯性影響最大的過渡墩，當主橋墩高為30 m時，主梁剛度對耦聯性影響較小;主橋墩高60 m時，主梁剛度的不同甚至會使耦聯性影響呈現相反的趨勢;當主墩墩高90 m時，主梁剛度對耦聯性的影響較大，但影響趨勢不變。

5 結論

本文通過建立有限元分析模型，同時考慮主梁和橋墩剛度的影響，從動力特性出發，分析了山谷地形橋梁的橫向基本周期變化、橫向地震慣性力分配特點以及相鄰聯橋梁之間的耦聯性，得到了以下結論:

(1)主梁剛度變化對山谷地形橋梁的橫向基本周期有明顯的影響。對于由橋寬變化引起的剛度變化，當主橋墩高相對不大時，主梁剛度增加會增大基本周期，但當主橋墩高相對很大時，主梁剛度增加會減小基本周期。

(2)山谷地形橋梁的主橋各墩承擔的地震慣性力，中間橋墩到過渡墩依次顯著減小，而引橋各墩隨著墩高降低所分擔的慣性力相應增大。主梁剛度的增加會明顯增大各墩分擔的地震慣性力，但不改變各墩間的分配規律。

(3)主橋的中間橋墩受耦聯性的影響不大，但引橋，特別是過渡墩受耦聯性的影響較大，而主梁剛度對相鄰聯地震耦聯性的影響也較大。

[1] 中華人民共和國住房和城鄉建設部. CJJ 166—2011城市橋梁抗震設計規范[S].北京:中國建筑工業出版社，2011.Ministry of Housing and Urban Rural Department of the People’s Republic of China.CJJ 166-2011 Code for seismic design of urban bridge[S].Beijing:China Building Industry Press，2011.(in Chinese)

[2] 李建中，范立礎.非規則梁橋縱向地震反應及碰撞效應[J].土木工程學報，2005，38(1):84-90.Li Jianzhong，Fan Lichu.Longitudinal seismic response and pounding effects of girder bridges with unconventional configurations[J].China Civil Engineering Journal，2005，38(1):84-90.(in Chinese)

[3] 孫廣俊，李鴻晶，趙鵬飛.非規則多跨簡支梁橋縱向地震反應及參數影響分析[J].防災減災工程學報，2013，33(4):441-448.Sun Guangjun，Li Hongjing，Zhao Pengfei.Longitudinal seismic response and parameter influence analysis for multi-span simply supported girder bridge with unconventional configurations[J].Journal of Disaster Prevention and Mitigation Engineering，2013，33(4):441-448.(in Chinese)

[4] 朱東生.簡支梁橋橫向地震反應研究[J].土木工程學報，2000，33(4):27-31.Zhu Dongsheng.Transverse seismic response of simply supported girder bridges[J].China Civil Engineering Journal，2000，33(4):27-31.(in Chinese)

[5] 張培君.非規則梁橋地震反應分析[D].上海:同濟大學，2005.Zhang Peijun.Longitudinal seismic response of girder bridges with unconventionalconfigurations[D].Shanghai:Tongji University，2005.(in Chinese)

[6] 葉愛君，管仲國.橋梁抗震[M].北京:人民交通出版社，2011.Ye Aijun，Guan Zhongguo.Seismic design for highway bridge[M].Beijing:China Communications Press，2011.(in Chinese)