熱軋層流冷卻對帶鋼板形的影響仿真分析

張 藝 李洪波 余志龍，3

(1：國家知識產權局專利局專利審查協作北京中心 北京100190；2：北京科技大學機械工程學院 北京100083；3：北京北方微電子基地設備工藝研究中心有限責任公司 北京100176)

·技術分析·

熱軋層流冷卻對帶鋼板形的影響仿真分析

張 藝①1李洪波2余志龍2，3

(1：國家知識產權局專利局專利審查協作北京中心 北京100190；2：北京科技大學機械工程學院 北京100083；3：北京北方微電子基地設備工藝研究中心有限責任公司 北京100176)

為分析某熱連軋生產線在開卷后出現的拱背或縱切分條后出現的翹曲問題，建立ANSYS有限元仿真分析模型，分析層流冷卻過程的帶鋼溫度分布和內應力情況。在確定邊界條件時，采用FLUENT軟件對帶鋼水冷換熱過程進行了數值仿真分析，得到換熱系數。利用ANSYS模型仿真分析了層流冷卻上下水比、前段和后段主冷模式以及初始橫向溫度分布對帶鋼內應力分布的影響，并根據分析結果，采取了改變上下水比、后段主冷模式，改善精軋橫向溫度不均勻分布等措施，使得拱背和縱切翹曲導致的板形缺陷改判率由4.2%降低到1.05%。

熱軋 層流冷卻 板形 內應力 有限元

熱軋帶鋼的軋后層流冷卻是提高鋼鐵材料性能和實現鋼種開發的重要工藝手段[1]。同時，層流冷卻過程造成的帶鋼溫度分布不均勻也成為影響帶鋼成品板形的重要因素。隨著對熱軋帶鋼板形精度要求的日益提高，層流冷卻對溫度不均勻分布并進而對板形產生的影響也越來越受到重視[2]。

王洪彬[3]、程杰鋒[4]、肖湖福[5]、徐小青[6]等采用有限差分法或有限單元法分析了層流冷卻后的溫度場分布；蘇艷萍[2]、Zhou Zhongqing[7]、Wang Xiaodong[8]、陳銀莉[9]等分析了層流冷卻后溫度場分布與帶鋼內應力之間的關系，分析了層流冷卻對板形的影響；王洪彬[3]、程杰鋒[4]、王曉東[10]等在研究過程中還考慮了層流冷卻過程中相變的作用。

中國某熱連軋機生產線的某熱軋產品，在開卷后常出現拱背或縱切分條后翹曲的問題，根據之前的文獻分析，認為與層流冷卻后的帶鋼溫度不均勻分布有關。因此針對典型品種規格的層流冷卻過程，建立了仿真分析模型，研究層流冷卻工藝對內應力的影響，為生產現場提出板形問題解決方案提供理論參考。

1 有限元仿真模型的建立

1.1 模型簡化和物理模型建立

在實際層流冷卻過程中，帶鋼在冷卻階段經歷不同的冷卻區域，邊界條件也隨之變化，這無疑增加了仿真計算的難度。參照前人研究方法，在建模時假定帶鋼在冷卻過程中靜止不動，而熱邊界條件在帶鋼表面移動[7，11]。

建立長度為1000mm，寬度為1800mm，厚度為9.8mm的帶鋼幾何實體模型。采用8節點六面體單元網格劃分，單元類型選取實體單元Solid70。由于帶鋼上下表面受到冷卻水射流沖擊發生換熱，因此采用映射網格非均勻劃分，由心部到表面網格逐漸變密，具體模型如圖1所示。

圖1 模型建立及網格劃分

1.2 邊界條件的確定

層流冷卻過程是一個非穩態的傳熱過程，這個過程中包括熱傳導、熱對流和輻射換熱三種基本方式。合理的確定各種邊界條件是提高仿真模型計算精度的關鍵。

高溫帶鋼在空冷的時候，主要的換熱是帶鋼與環境空氣之間的對流換熱，以及帶鋼對外界的輻射換熱。兩種換熱同時進行，因此其綜合換熱系數可表示為：

(1)

式中hr—空冷輻射換熱系數，W/(m2·K)；hc—對流換熱系數，W/(m2·K)；Ts—帶鋼的表面溫度，K；T∞—帶鋼的環境溫度，K；σ—Boltzmann常數，取5.67×10-8W/(m2·K4)；ε—帶鋼的輻射率，取0.8。

帶鋼經過水冷區，冷卻水在帶鋼表面形成射流沖擊區和穩態膜沸騰區，且上下表面差異較大需分別處理。因此，分為帶鋼上表面射流沖擊換熱、下表面射流沖擊換熱和穩態沸騰區換熱三部分。采用FLUENT軟件對帶鋼水冷換熱過程進行了數值仿真分析，初始條件如表1所示。仿真得到的換熱系數分布圖如圖2所示。

表1 數值仿真的初始條件

1.3 材料物性參數的確定

材料物性參數是隨著溫度而變化的，對計算結果有很大影響。其中導熱系數、比熱等需要通過模擬實驗來確定，結果如表2所示。

為了簡化計算模型，在熱應變增量中將相變增量換算進去，即在熱膨脹系數的基礎上加上相變導致的膨脹部分。根據帶鋼冷卻過程中的組織轉變模擬模型計算，得到組織轉變后的成分是92.63%鐵素體，6.93%的珠光體，0.46%的馬氏體。通過考慮組織成分轉變的影響，得出了考慮相變因素的材料物性參數隨溫度的變化規律如表3所示。

1.4 初始溫度場的確定

熱軋帶鋼精軋結束后，已經具有了特定的溫度分布，作為初始條件，在計算時首先加載溫度分布。

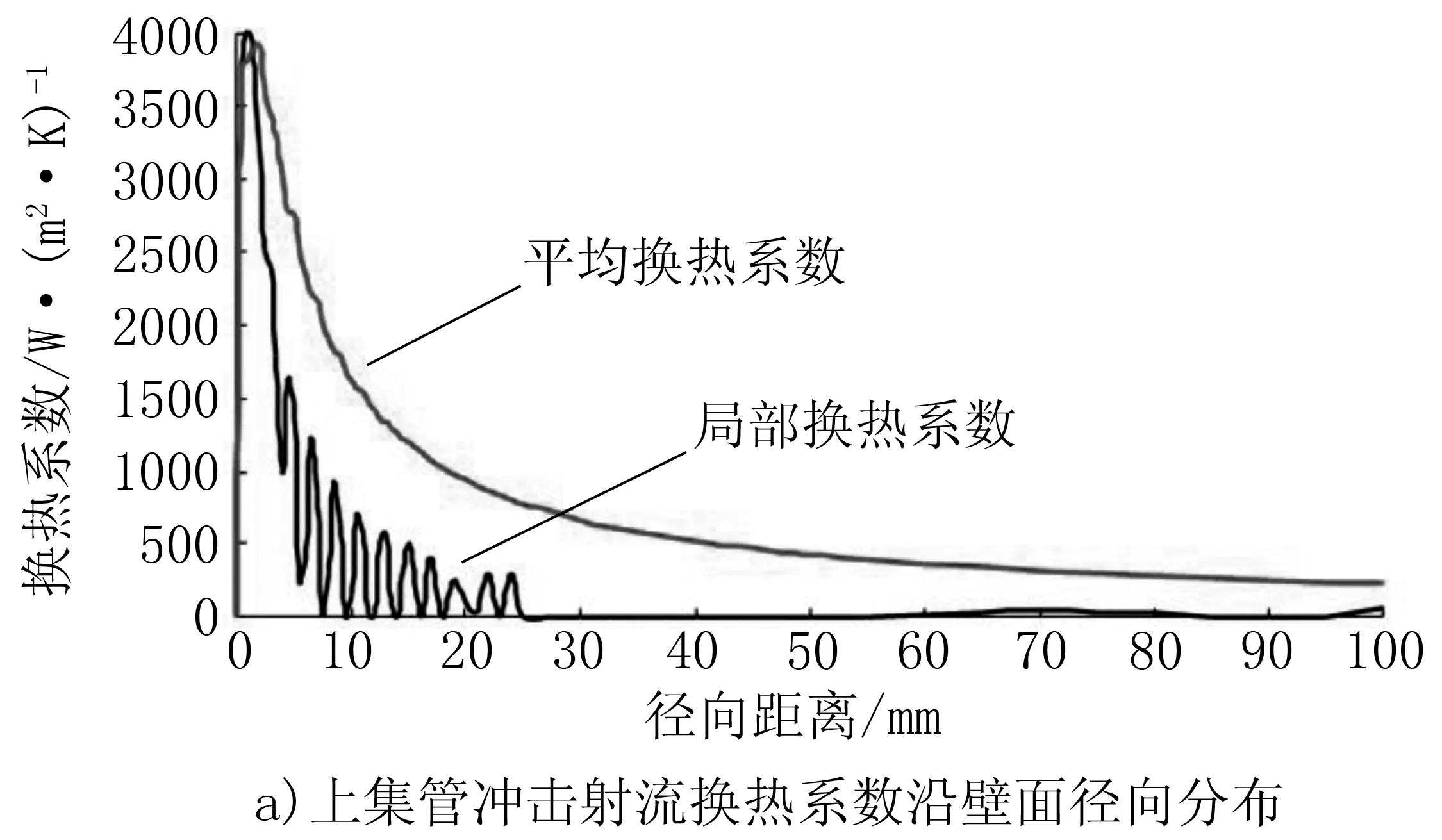
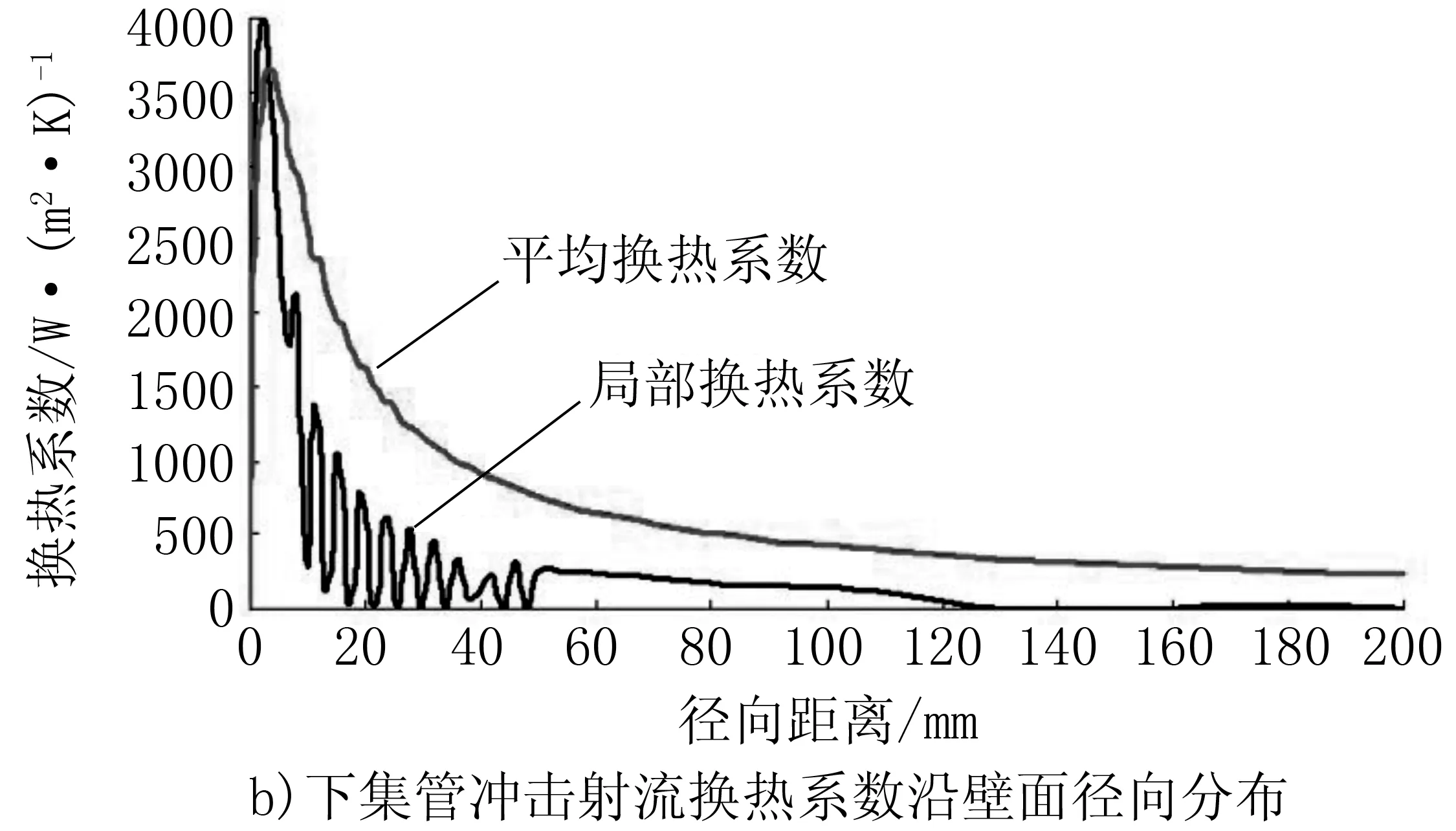
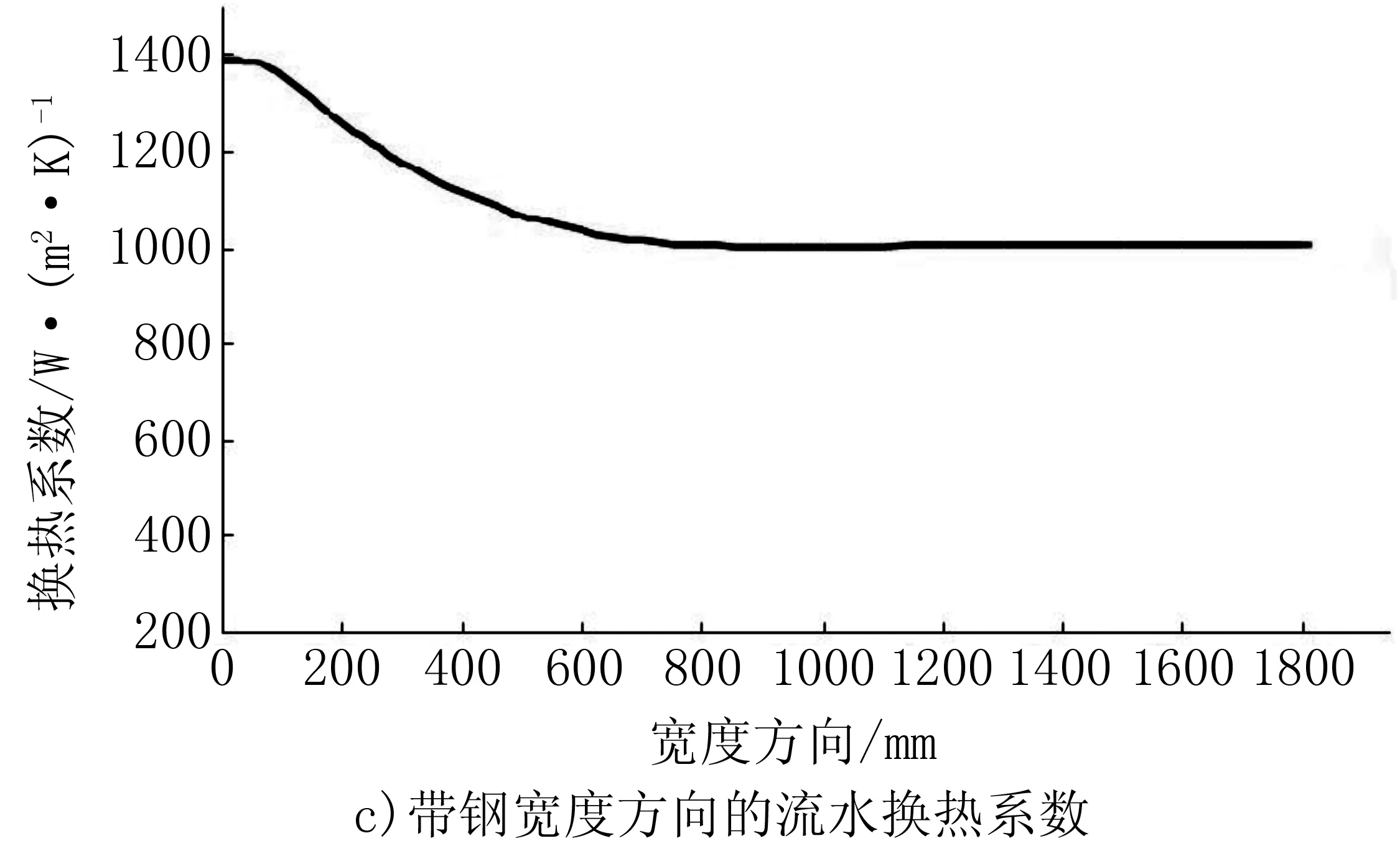
圖2 換熱系數分布圖

在精軋機出口處采用紅外熱像儀對帶鋼的橫向溫度進行測量，并利用最小二乘法對實際的表面溫度場進行曲線擬合，作為初始溫度的輸入。

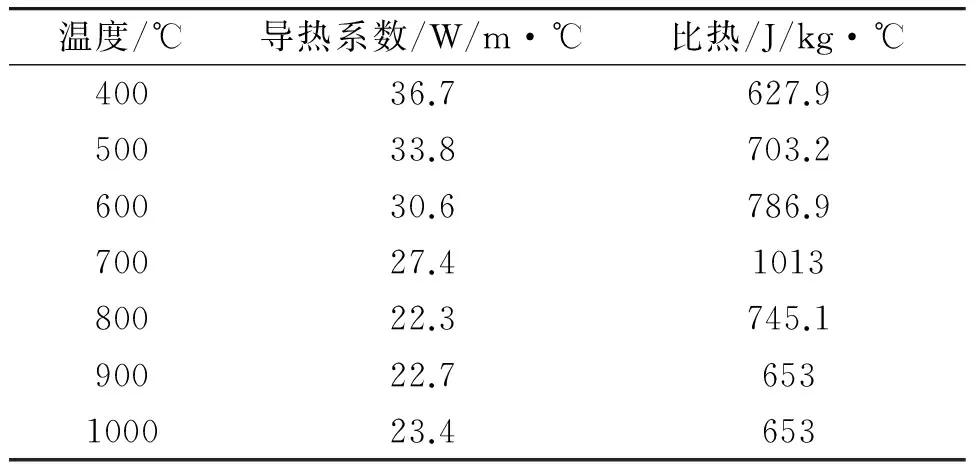
表2 導熱系數、比熱隨溫度變化關系的確定

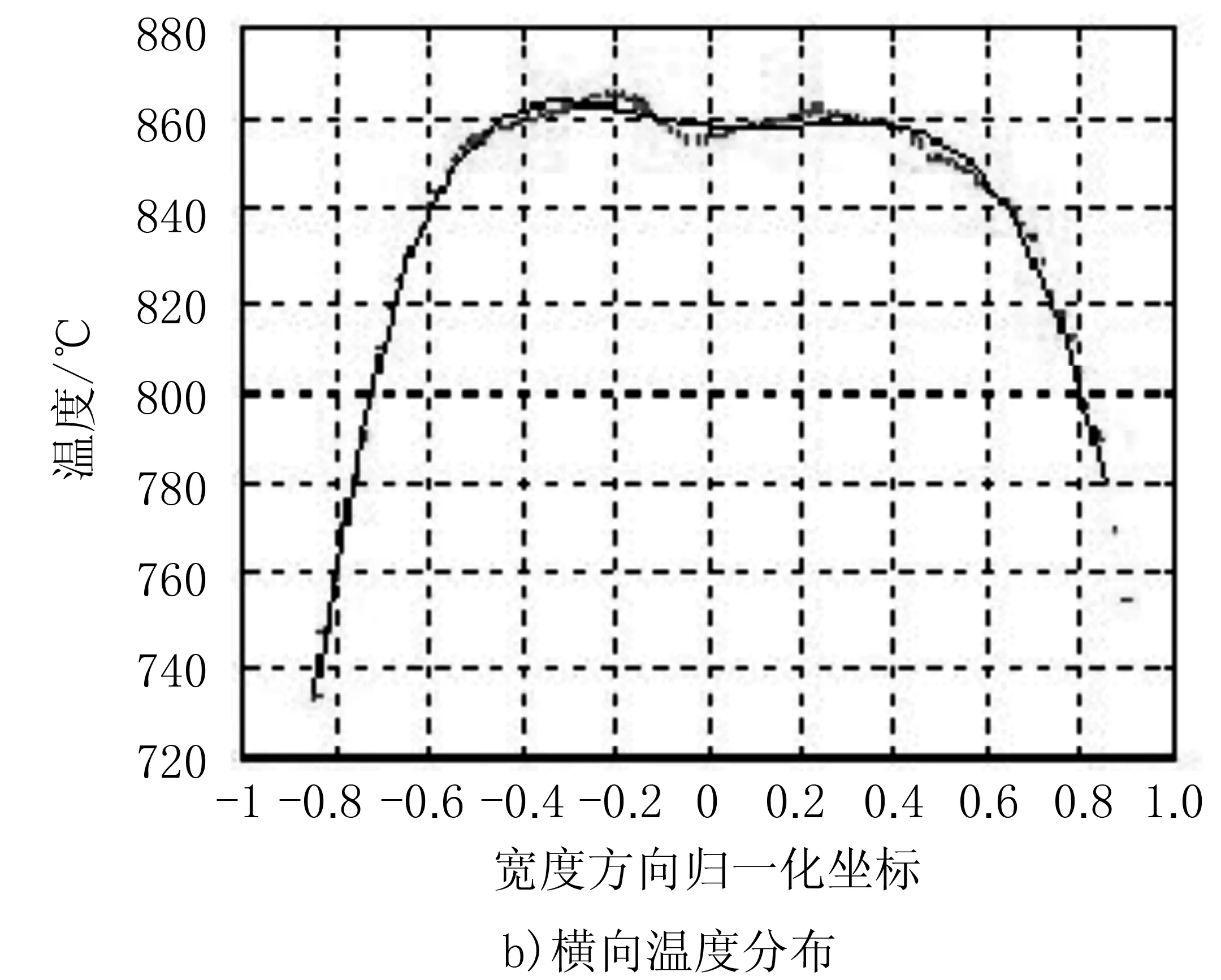
圖3 熱像儀熱像圖及橫向溫度分布

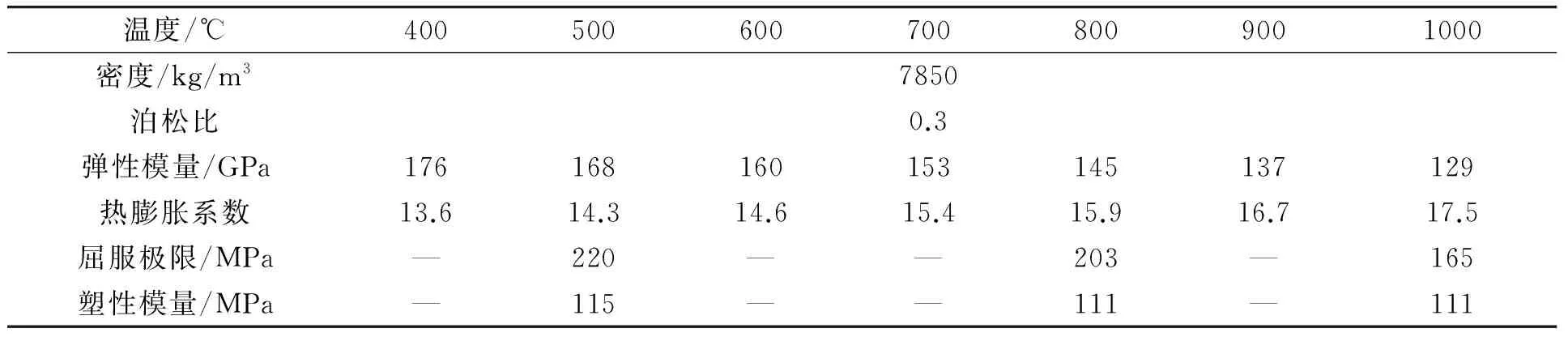
溫度/℃4005006007008009001000密度/kg/m37850泊松比0.3彈性模量/GPa176168160153145137129熱膨脹系數13.614.314.615.415.916.717.5屈服極限/MPa—220——203—165塑性模量/MPa—115——111—111

圖3為某卷帶鋼的橫向溫度分布測量結果，可以看出，帶鋼的寬度方向溫度存在較大的溫度差，且邊部溫降較大。

1.5 層流冷卻工藝條件

仿真模型是以某熱軋廠某鋼種的實際軋制工藝條件為計算基礎的，層冷前溫度850℃，終冷溫度620℃，冷卻水溫度20℃。

冷卻策略包括前段主冷模式和后段主冷模式：

1.5.1 前段主冷模式

當產品需要在溫度較高區快速降溫時，采用前段主冷模式，此時優先集中將層流冷卻區入口側的集管閥門打開，快速冷卻區集中在層冷區前部。

1.5.2 后段主冷模式

當產品需要在溫度較低區快速降溫時，采用后段主冷模式，此時優先集中將層流冷卻粗冷區出口側的集管閥門打開，快速冷卻區集中在層冷主冷區后部。

仿真時，前段冷卻模式前段開啟8組集管，后段開啟4組集管；后段冷卻模式前段開啟4組集管，后段開啟8組集管。

2 仿真結果分析

2.1 上下水比對板形的影響

在層流冷卻過程中，為了保障帶鋼的板形良好，不出現拱背現象，必須要保證上下表面的溫差較小。要保證帶鋼的上下表面冷卻均勻一致，可以通過調整帶鋼冷卻上下水比進而達到控制帶鋼上下表面溫差，使帶鋼獲得良好的板形。因此，在前段主冷模式下，對上下水比依次為1∶1.25，1∶1.3，1∶1.35 的工況進行仿真分析，得到帶鋼上下表面溫差和三維應力云圖，如圖4所示。

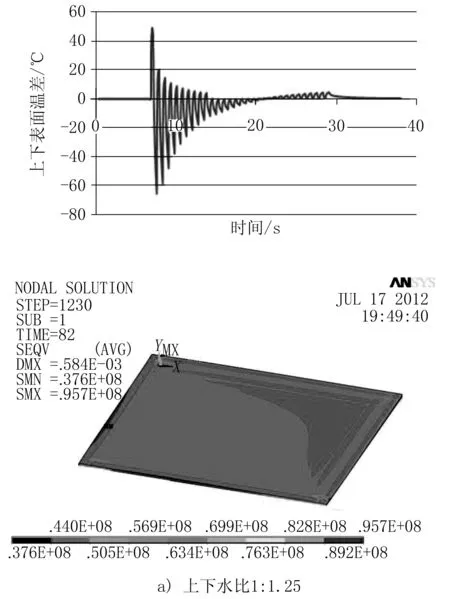
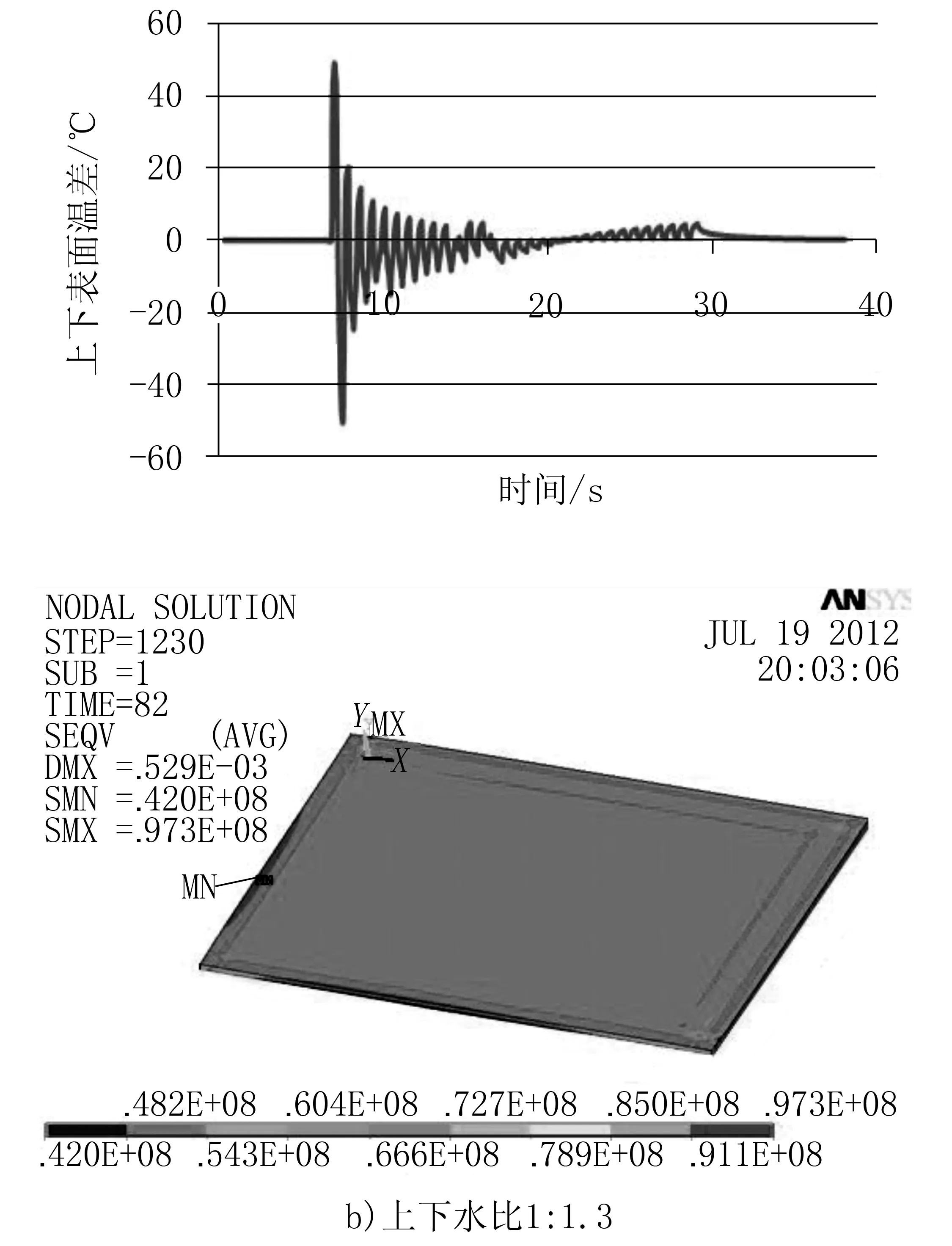
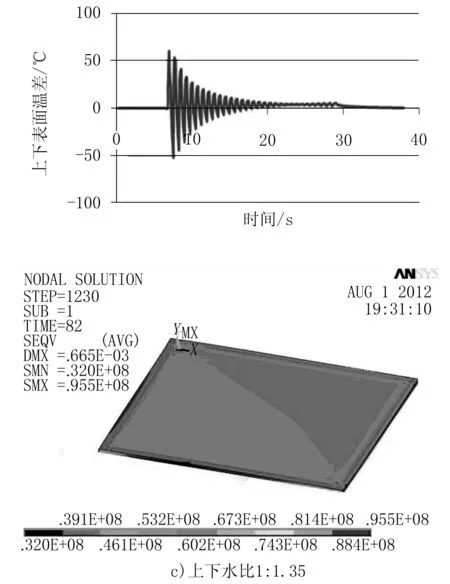
圖4 帶鋼上下表面溫差及三維應力云圖

對比分析可以看出：隨著帶鋼上下水比從1∶1.25到1∶1.35的變化，帶鋼上下表面的溫差也隨之變化；1∶1.25時上表面溫降比下表面快，溫差基本為負， 1∶1.3左右時，上下表面溫降差不多，此時的上下表面溫差基本對稱，水比1∶1.35左右時，上表面溫降比下表面慢，最后溫差為正；從帶鋼的三維應力圖可看出在上下水比為1∶1.3左右時，帶鋼表面的應力值基本趨于一致，最后帶鋼的殘余應力較小。

2.2 冷卻模式對板形的影響

對前段主冷模式和后段主冷模式進行仿真分析，圖5分別為前段主冷和后段主冷下的應力分布。

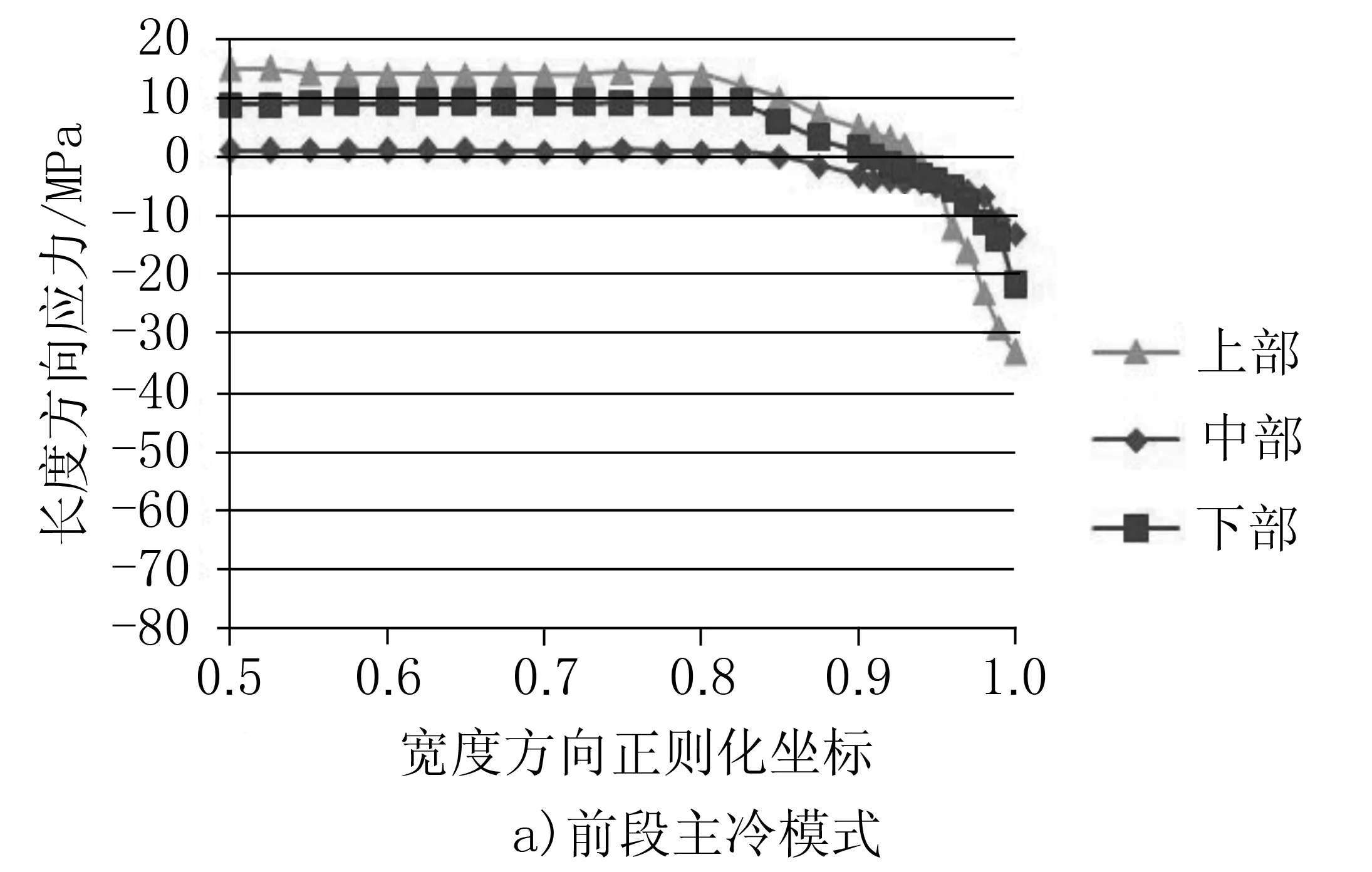
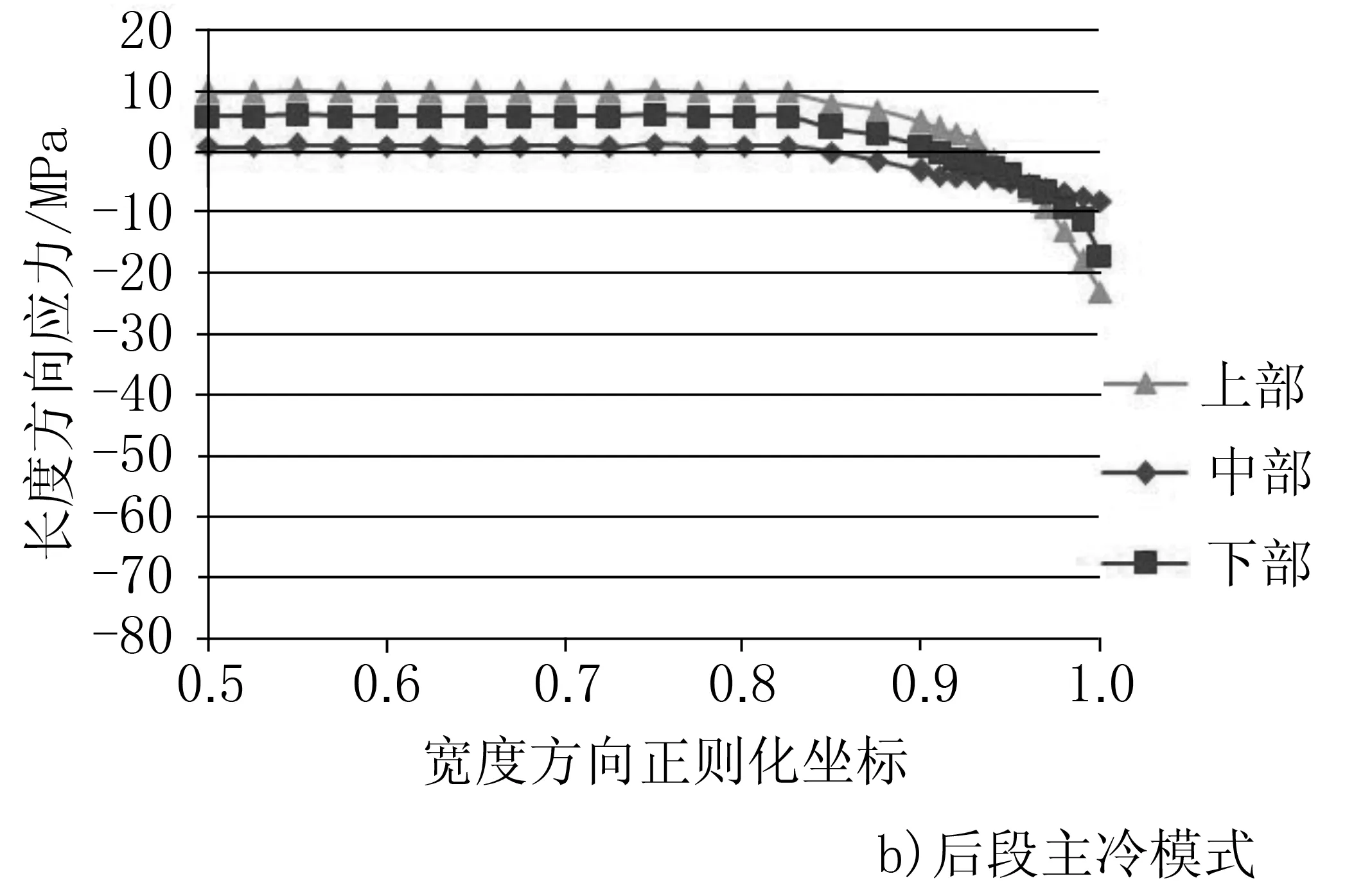
圖5 應力沿寬度方向變化曲線

可以看出，后段冷卻的應力曲線的分布與前段冷卻模式相似，但在后段冷卻模式下，內應力相對較小，最大應力僅為-20MPa左右，不同厚度截面上的應力相比于前段冷卻模式也更為均勻。因此，后段冷卻模式對于某鋼種更利于形成良好的板形。

2.3 初始橫向溫度分布對板形的影響

圖6a)和b)分別是加載均勻初始橫向溫度分布和加載圖3熱像儀所測橫向溫度分布的帶鋼寬度方向的應力情況。

可以看出，即使精軋機出口處的初始橫向溫度分布均勻，帶鋼邊部由于冷卻不均仍存在普遍的溫降現象，邊部的溫降導致熱應力在帶鋼邊部受壓應力，帶鋼中部受拉應力。熱像儀所測帶鋼最大溫差達到120℃，此時帶鋼邊部表面壓應力最大可達-80MPa，主要集中在距離帶鋼邊部100mm的范圍內。

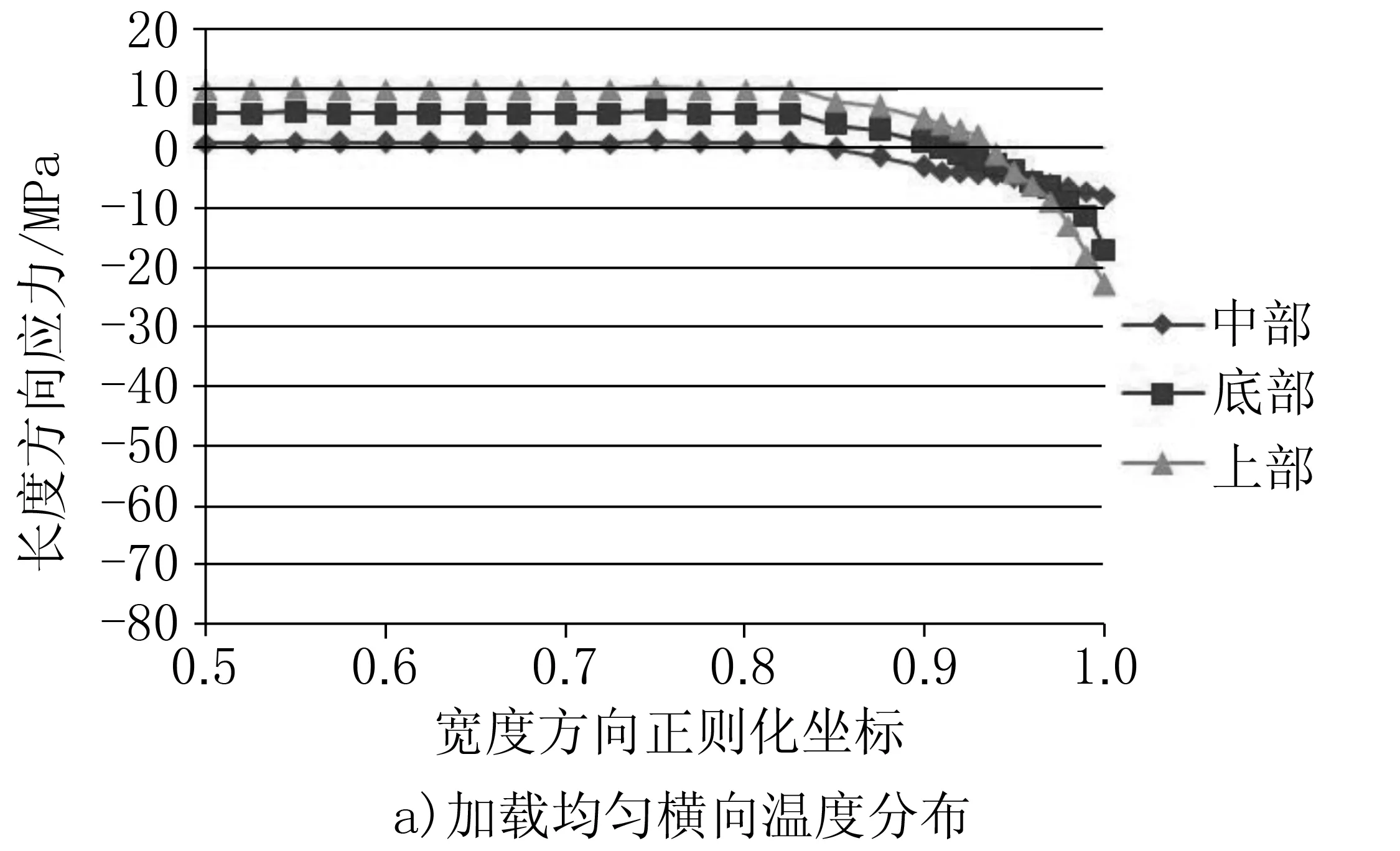
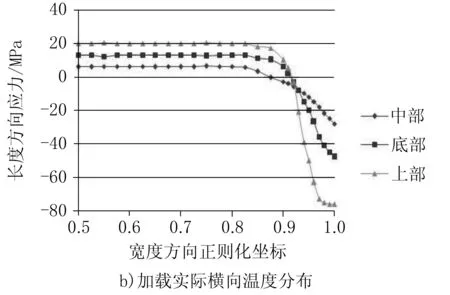
圖6 應力沿寬度方向變化曲線

帶鋼初始橫向溫度分布直接影響帶鋼層流冷卻后的應力分布，初始橫向溫差越大，帶鋼邊部與中部的應力差越大，邊部形成的塑性應變值也越大，這對軋后帶鋼板形會帶來一定的不良影響，因此精軋出口處帶鋼橫向溫度的均勻性是保證軋后冷卻板形良好的重要條件。

3 結論

1)隨著帶鋼上下水比從1∶1.25到1∶1.35變化，帶鋼上下表面的溫差也隨之變化。某鋼種冷卻的最佳上下水比在1∶1.3左右，此時帶鋼表面的應力值基本趨于一致，最后帶鋼的殘余應力較小。

2)后段主冷模式帶鋼的應力分布與前段主冷模式相似，但在后段主冷模式下，產生的應力相對較小，且不同厚度截面上的應力相比于前段冷卻模式也更為均勻。

3)帶鋼層流冷卻后的應力分布直接受帶鋼初始橫向溫度分布的影響，初始橫向溫差越大，帶鋼邊部與中部的應力差越大，這對軋后帶鋼板形會帶來一定的不良影響。

4)根據分析結果，采取了改變上下水比、采取后段主冷模式，改善精軋橫向溫度均勻分布等措施是，使得某鋼種拱背和縱切翹曲導致的板形缺陷改判率由4.2%降低到1.05%。

[1]黃全偉，韓斌，譚文，等.層流冷卻溫度場數學模型的研究現狀[J].鋼鐵研究，2013，Vol.41(1)：59-62.

[2]蘇艷萍，楊荃，何安瑞，等.ASP1700熱軋層流冷卻過程中影響板形變化的熱應力求解[J].鋼鐵，2008，Vol.43(5):55-60.

[3]王洪彬，孫正旭，孫麗榮，等.層流冷卻過程中帶鋼溫度場的數值模擬[J].冶金設備，2008(6)：18-22.

[4]程杰鋒，劉正東，唐廣波.帶鋼層流冷卻過程數值模擬及卷取溫度預測分析[J].鋼鐵，2010，Vol.45(11)：57-61.

[5]肖湖福，楊玉芳，牟世學，等.基于Ansys有限元的帶鋼層流冷卻工藝的確定[J].冶金設備，2012(S2)：1-4.

[6]徐小青，韓慶，傅松林.熱軋帶鋼層流冷卻過程的溫度預測模型[J].鋼鐵研究學報，2012，Vol.24(12):23-27.

[7]Zhou Zhongqing，Lam YeeCheong，P F Thomson，et al. Numerical analysis of the flatness of thin rolled steel strip on the runout table[J].Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture，2007，Vol.221(2)：241-254.

[8]Wang Xiaodong，Yang Quan，He Anrui，et al. Calculation of thermal stress affecting strip flatness change during run-out table cooling in hot steel strip rolling[J].Journal of Materials Processing Technology，2008，Vol.207(1-3)：130-146.

[9]陳銀莉，余偉，蘇嵐，等.熱軋帶鋼層流冷卻過程中殘余應力分析[J].材料熱處理學報，2010，Vol.31(6)：155-160.

[10]王曉東，何安瑞，楊荃，等.熱軋帶鋼層流冷卻過程中溫度與相變耦合預測模型[J]. 北京科技大學學報， 2006，Vol.28( 10)：964-968.

[11]王曉東.層流冷卻影響熱軋帶鋼板形機理及控制策略研究[D].北京：北京科技大學，2007.

Simulated Analysis of the Influence of Laminar Cooling Process for Strip Flatness in Hot Rolling

Zhang Yi1Li Hongbo2Yu Zhilong2，3

(1:Patent Examination Cooperation Center of the Patent Office, SIPO, Beijing, Beijing 100190；2:School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083;3:Beijing North Microel Ectronics, Beijing 100176)

In order to analyze the strip C-shape wrap problem after uncoiling and buckling problem after length cutting, an ANSYS finite element model was established to calculate the strip temperature and internal stress distribution after laminar cooling. For giving an accurate boundary condition, the heat transfer coefficient in water cooling was calculated by a FLUENT model of strip water cooling process. Then the influence of the ratio of upper and lower water flow, the front or end section main cooling mode, the original temperature distribution on the strip internal stress were analyzed by the ANSYS model. Based on the analyzing result, the ratio of upper and lower water flow was changed, the end section main cooling mode was come into service, and the original temperature distribution was improved, then the strip defect rate of C-shape wrap problem and buckling problem was drop from 4.2% to 1.05%.

Hot rolling Laminar cooling Flatness Stress Finite element method

張藝，女，1983年出生，畢業于北京科技大學材料與科學工程學院，專利審查員，主要人事機械加工方面的專利審查

TG335.5 TB115

A

10.3969/j.issn.1001-1269.2015.05.006

2015-05-12)