在線檢測介質損耗角的矩陣束方法

董 爽 李天云 王 永 彭茂君

（1.東北電力大學輸變電技術學院 吉林 132012

2.國網北京市電力公司 北京 100031）

0 引言

隨著電力系統向超高壓、大容量的方向發展，如何保證電氣設備的安全穩定運行變得尤為重要。而電氣設備（尤其是高壓設備）事故大部分是由絕緣損壞引起的，因此及時有效地發現絕緣存在缺陷，對于保障電網安全運行具有重要意義[1,2]。介質損耗角（介損角）是衡量電容性電氣設備絕緣水平的重要指標，其理論值很小，通常約為0.001～0.02rad，實際監測時很容易因方法本身誤差及現場各種干擾因素而湮沒真實值。故介損角測量的準確度與抗干擾能力[3-5]受到了國內外研究與工程領域的廣泛關注。

目前，介損角測量總體上分為硬件實現和軟件實現。硬件方法主要以電橋平衡法[6]和過零比較法[7]為代表。因硬件處理環節較多，累計誤差較大等問題，硬件法的準確度、穩定性難以保證，抗干擾能力較差。軟件方法主要以信號處理方法為主，通過硬件獲取電壓、電流信號，采用一種或多種信號處理方法來抑制噪聲、諧波等干擾的影響，避免增加硬件電路的復雜性，較為靈活，是目前介損角測量的發展方向。相關函數法[8,9]利用電壓、電流信號的自相關和互相關函數計算介損角，相關函數的計算要求積分區間為整周期，當電網頻率波動時，就造成采樣頻率與信號頻率不同步，從而使測量結果存在較大誤差。高階正弦擬合法[10,11]和正弦波參數法[12,13]均是利用最小二乘算法或三角函數正交性算法求得正弦波參數，計算出介損角。前者不能克服相位漂移、諧波含量及噪聲對測量準確度的影響；后者雖考慮了噪聲和諧波的干擾，但測量準確度仍受電網頻率波動的限制。諧波分析法[14-16]利用離散傅里葉變換對電壓、電流信號進行諧波分析計算介損角，該方法計算簡單，在一定程度上克服了諧波的影響，是介損角測量的典型方法，但非同步采樣會產生頻譜泄漏和柵欄效應，影響介損角測量的準確度。

矩陣束算法是一種非迭代算法，運算量較小，不存在累積誤差，是一種有效的陣列信號參數識別方法。本文利用矩陣束方法準確提取電容性設備的運行電壓、泄漏電流信號中的基波電壓和電流的初始相位，從而實現介損角的測量。該方法采用內積形式，并引入奇異值分解和矩陣的低秩近似等方法，更好地抑制了噪聲干擾，同時提高了計算效率。仿真結果表明，該方法提高了介損角測量的準確度和穩定性。

1 介損角基本概念

電介質在電壓或電場的作用下，會產生電導損耗和極化損耗，統稱介質損耗。介質損耗將電能大部分轉換為熱能，使絕緣的熱量積聚，溫度升高，造成絕緣老化甚至熔化、焦化。電介質在交流電壓作用下，等效電路及其相量關系圖如圖1所示。通過電介質的電流I˙可分為有功分量I˙R和無功分量C，I˙C超前于I˙的相位角δ稱之為介質損耗角。由圖1b所示相量圖可見，δ的數字化測量可通過提取流經設備的電流、電壓的基波分量、U˙的相位差φ得到

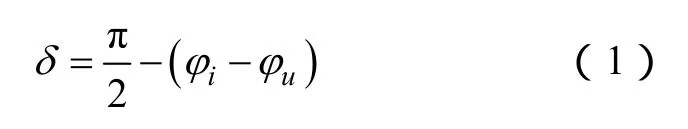
式中，iφ和uφ分別為基波電流、電壓的初相位。

圖1 等效電路及相量關系圖Fig.1 Equivalent circuit and vector diagram

2 矩陣束算法

矩陣束算法是20世紀80年代末、90年代初由Y.Hua和T.K.Sarker提出的一種參數識別估計方法[17,18]。

設信號可以表示為M個模態的指數函數的線性組合形式，即

式中，n(t)為系統噪聲；x(t)為不含噪聲的信號；y(t)為實測包含噪聲的信號；對第i個模態，Ri為幅值；si=-αi+ jωi，αi為衰減或阻尼因子，ωi為角頻率，ωi=2πfi。式（2）的離散形式為

式中，Ts為采樣間隔；k=0,1,2,…,N-1，N為最大采樣點數；zi=esi Ts。

由采樣序列yk(k=0,1,2,…,N-1)構造矩陣Y

式中，L為矩陣束參數，合理地選取L值可以有效抑制噪聲的影響。通常，L在N/4～N/3之間取值[17]。

對矩陣Y進行奇異值分解

式中，U、V分別為(N-L)×(N-L)階和(L+1)×(L+1)階的正交矩陣；∑為對角陣，其對角元素σi為Y的奇異值，且按降序排列。

若測量數據不含噪聲，則Y有M個非零奇異值。但在實際測量中，由于噪聲的存在，矩陣∑對角元素中原來為 0者可能不再為0，若噪聲相對于主導信號較弱，則其值一般較小。因此，對奇異值進行適當截取，只保留其中M個最大的奇異值，可以有效減小噪聲對參數估計準確度的不良影響。通常將滿足條件σ σ＞1 0-p（p為十進制的有效位數）

imax的最大下標記為最大模態數M。

在已確定最大模態數M條件下，由∑的M個主奇異值構造新陣∑′，從對矩陣Y進行奇異值分解得到矩陣V取出V中前M個主導奇異向量構成(L+1)×M的矩陣V′，并從V′中刪去最后一行生成矩陣V1′，刪去第一行生成矩陣V2′。

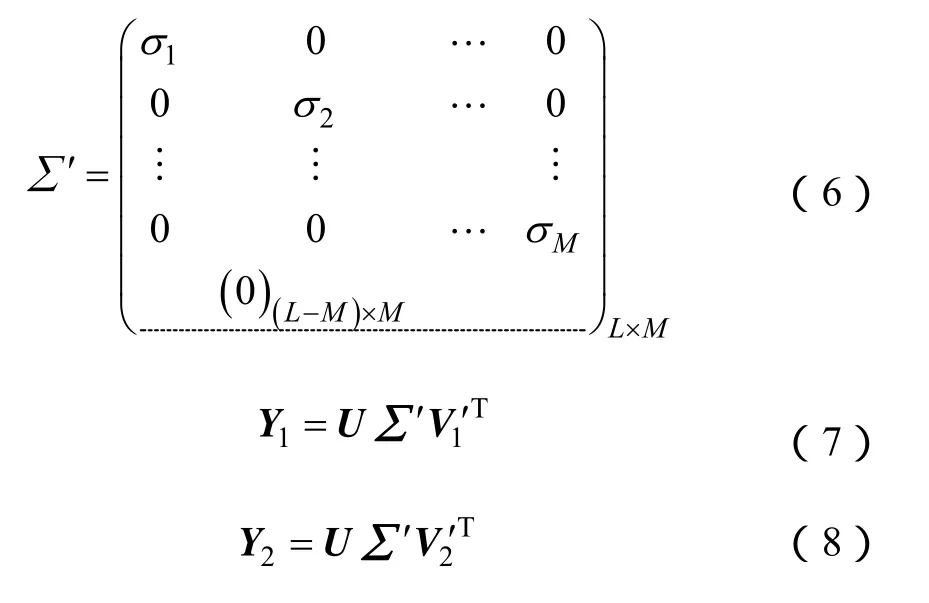
Y1、Y2可認為已經不存在噪聲的影響，即

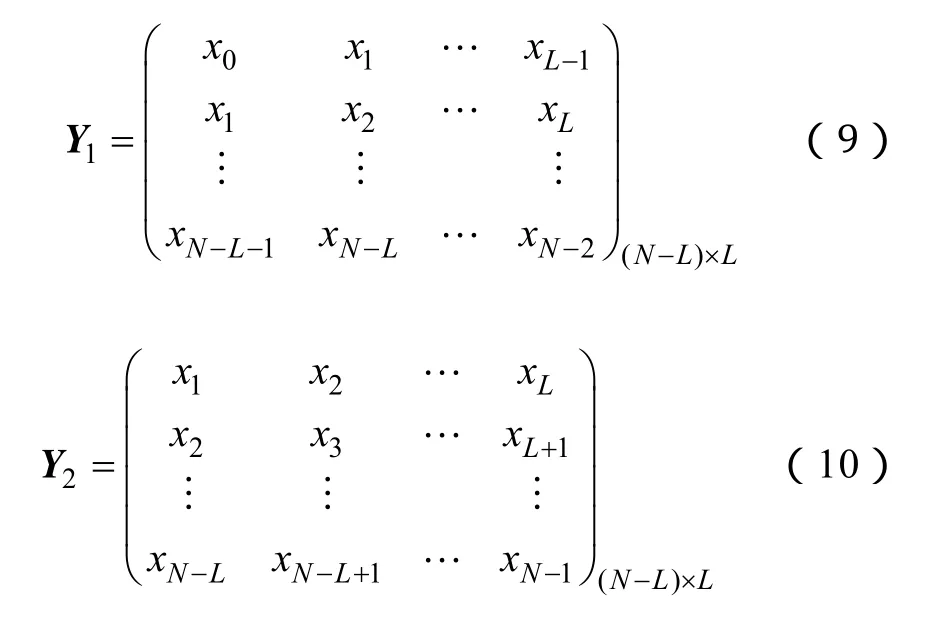
由Y1、Y2構造矩陣束21λ-YY，并將代入21λ-YY整理得

式中，I為M×M階單位陣

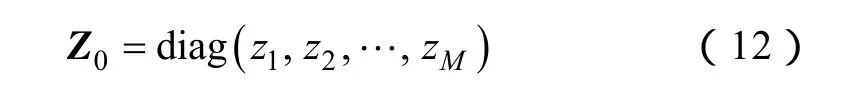
式（11）中，當λ與所有的極點zi都不相等時，Y2-λY1的秩為M；當λ與某一極點zi相等時，矩陣（Z0-λI）的第i行全為0，Y2-λY1的秩降為M-1。因此，信號的極點zi（i=1,2,…,M）即為矩陣束{Y2，Y1} 的廣義特征值，從而求解信號極點的問題就轉化為求解式（16）的廣義特征值。

式中，Y1+為Y1的偽逆矩陣。

在估計出最大模態數M和所有極點zi后，幅值Ri可通過求解下列最小二乘問題得到

求解出iz和iR后，進而可以求得信號的幅值、相位、角頻率和衰減因子。

3 仿真分析

設電壓、電流信號分別為

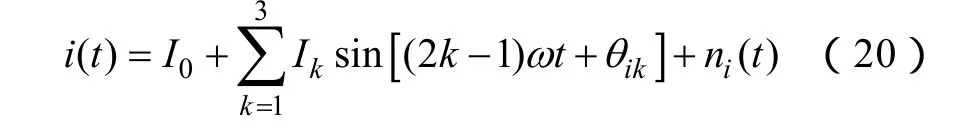
式中，U0、I0分別為電壓、電流信號的直流分量；Uk、Ik分別為電壓、電流信號k次諧波的幅值；θuk、θik分別為電壓、電流諧波信號的初始相位；ω為角頻率；nu(t)、ni(t)分別為電壓、電流信號中的噪聲分量。

模型階數M的確定是矩陣束算法中的一個關鍵。對于一個含有未知成分的待分析信號，可采用穩定圖或奇異值差值法等方法確定其有效階數。而對于介損角的檢測，采集到的信號主要成分如式（19）和式（20）所示，7次及以上諧波分量比重極小，可視為噪聲。當信號不含噪聲或信號的信噪比很高時，虛假模態的奇異值為零；當信號的信噪比較大時，真實模態的奇異值較大，而虛假模態的奇異值很小，且存在明顯的突變。故本文取p=2，得模型階數M=7。

仿真計算時，如無特殊說明，相關參數如下：采樣頻率 5kHz，采樣時間 0.1s，真實介損角δ=0 .003rad，基波頻率f=50.5Hz，3次、5次諧波幅值分別取基波分量的 10%和 2%。為全面地反映信號初始相角對介損角檢測結果的影響，信號的初始相角在[0，2 π)之間取100個測量點。通過仿真給出了該方法在考慮電網頻率波動、諧波和直流分量變化、介損角真實值不同、采樣頻率和采樣點數變化以及噪聲擾動情況下，介損角計算誤差的變化情況，并與EMD-正弦波參數法[12]、隨機子空間-最小二乘算法（SSI-LS）[19]進行比較。

3.1 頻率波動對介損角檢測的影響

信號基波頻率在49.5～50.5Hz范圍內取5個觀測點，介損角誤差隨信號初始相角的變化情況如圖2所示。

由圖2可以看出，考慮諧波存在情況下，頻率在電力系統正常波動范圍內變化，信號初始相位在[0，2 π)范圍內變化，介損角計算的誤差絕對值均小于 1.5×10-13rad，計算準確度很高，且計算誤差變化不明顯。頻率波動及初始相角不同對本文算法基本無影響。

3.2 諧波分量對介損角檢測的影響

電力系統諧波分量中以3次、5次諧波為主，設 3次、5次諧波分量占基波分量的比值分別在0.05～0.80、0.01～0.16之間變化，依次對應遞增等間隔取 16個觀測點，介損角誤差變化情況如圖3所示。

圖3 諧波分量對介損角檢測的影響Fig.3 Influence of harmonic component on measurement of dielectric loss angle

由圖3可以看出，當諧波分量占基波分量的比值在預設范圍內變化時，介損角誤差絕對值的最大值均小于2×10-13rad，誤差的標準差均小于0.55×10-13rad，且波動很微小，計算準確度完全滿足介損角測量的要求，且諧波分量幅值變化時，介損角計算誤差變化并不明顯，對本文算法基本無影響。

3.3 直流分量對介損角檢測的影響

在實際的介損角測量中，電壓、電流信號的采集存在著零點漂移現象，這會在信號中產生直流分量。電流信號的采集來自絕緣介質的泄漏電流，通常比較微弱，現場測試時容易受到干擾，導致電流信號發生零點漂移；而電壓信號來自電壓互感器，信號較強，零點漂移相對很小。為更好地反映零點漂移對本文算法計算結果的影響，電壓信號中直流分量占基波分量的比值取 5%，電流信號中直流分量占基波分量的比值在 0～80%之間變化，每增加5%取一個觀測點，介損角計算誤差變化情況如圖4所示。

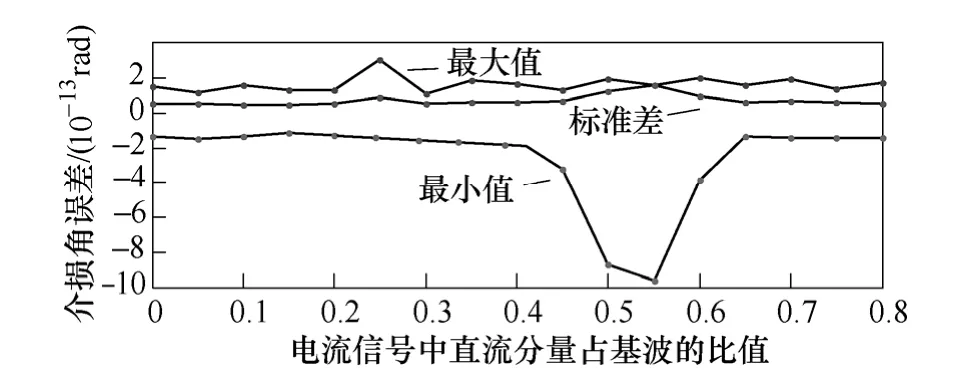
圖4 直流分量對介損角檢測的影響Fig.4 Influence of direct bias on measurement of dielectric loss angle

由圖4可以看出，電流信號中直流分量占基波分量的比值從0增加到0.8，介損角誤差絕對值的最大值均小于1×10-12rad，誤差變化較小，電流信號中無直流分量且直流分量占基波分量80%時，計算所得介損角誤差絕對值基本相等；介損角誤差的標準差均小于 2.0×10-13rad，波動很微小。直流分量幅值變化對本文算法基本無影響。

3.4 介損角真實值對檢測的影響

介損角的真實值通常較小，為更好地反映介損角的真實值對本文算法準確度的影響，介損角的取值從 0.002～0.02rad，每遞增 0.002rad取 1個觀測點，計算誤差的變化情況如圖5所示。

由圖5可以看出，隨著介損角真實值的增大，誤差絕對值的最大值均小于2×10-13rad，準確度較高，誤差變化并不明顯；介損角誤差的標準差均小于 0.5×10-13rad，且波動很微小。介損角真實值的大小對本文算法基本無影響。

圖5 介損角真實值對介損角檢測的影響Fig.5 Influence of real value on measurement of dielectric loss angle

3.5 采樣頻率對介損角檢測的影響

采樣時間固定取0.1s，采樣頻率在1～5kHz范圍內變化，每增加500Hz取一個觀測點，介損角計算誤差的變化情況如圖6所示。

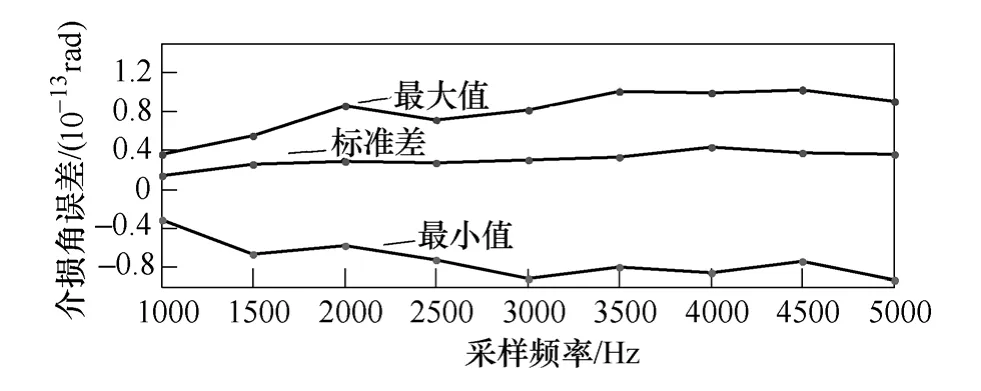
圖6 采樣頻率對介損角檢測的影響Fig.6 Influence of sampling frequency on measurement of dielectric loss angle

由圖6可以看出，采樣頻率在預設范圍內變化時，介損角誤差絕對值的最大值均小于1.2×10-13rad，誤差及其變化相當微小，介損角誤差的標準差均小于0.4×10-13rad。采樣頻率為1kHz時，介損角誤差絕對值都在 10-14rad數量級，已經可以獲得較高的準確度。采樣頻率的變化對本文算法基本無影響。

3.6 采樣點數對介損角檢測的影響

采樣頻率固定取5kHz，采樣點數從100點增加到1 000點，介損角計算誤差的變化情況如圖7所示。

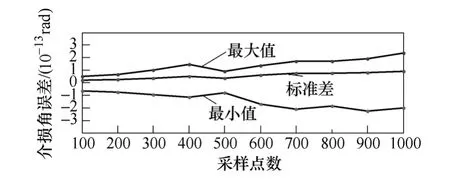
圖7 采樣點數對介損角檢測的影響Fig.7 Influence of sampling number on measurement of dielectric loss angle

由圖7可以看出，采樣點數為 100，即僅取一個周期內的采樣值時，介損角誤差絕對值都在10-14rad數量級，已能獲得較高的準確度。隨著采樣點數的增加，介損角誤差絕對值的最大值仍都小于 2.5×10-13rad，變化幅度很小；介損角誤差的標準差小于 1.0×10-13rad，波動幅度很微小。采樣點數的變化對本文算法的計算準確度基本無影響。

3.7 噪聲對介損角檢測的影響

由于待檢測的設備安裝位置和外界電磁干擾等因素的影響，現場采集的信號往往受到不同程度的噪聲污染。考慮現場噪聲的影響，信噪比在 15～40dB范圍內每增加5dB取1個觀測點，計算所得介損角的誤差見表1。

表1 白噪聲對介損角檢測的影響Tab.1 Influence of white noise on measurement of dielectric loss angle（單位：10-4rad）

由表1可知，隨著信噪比的增大，介損角的計算誤差明顯呈下降趨勢。當信噪比不小于25dB時，介損角計算誤差的絕對值均小于 2×10-3rad，準確度達到 10-4數量級及以上，誤差的標準差均小于0.5×10-3rad，即當信噪比不小于 25dB時，本文算法的計算準確度能夠滿足介損角檢測的精度要求；當信噪比小于 25dB時，可利用低通濾波器對原始信號進行去噪后，再用矩陣束算法進行介損角檢測。

3.8 算法的計算速度

在Matlab R2012環境下編程實現矩陣束算法，計算介損角所用時間為0.066 s。可見，矩陣束算法計算速度較快，且編寫程序時此法簡便，易于實現。

3.9 幾種方法比較

為驗證矩陣束算法的有效性，本文與 EMD-正弦波參數法、隨機子空間-最小二乘算法（SSI-LS）進行了比較。參數如下：真實介損角為δ=0 .008 7rad，3次、5次諧波分別取基波分量的10%和2%，采樣頻率為1kHz，采樣時間為0.1s，基波頻率為50.3Hz，電壓、電流信號中直流分量分別占基波分量的10%和 50%，初相角在 0～π/2之間取 100個點，信噪比為30dB。檢測結果列于表2，δmean、δmean-δ分別表示計算所得介損角的平均值及誤差，Δδmax、Δδmin分別表示介損角誤差的最大值、最小值。

表2 三種方法的介損角檢測結果Tab.2 Results of three detection methods（單位：10-4rad）

由表2可見，三種方法所計算的介損角平均值的誤差均小于 0.002rad，能夠滿足介損角的測量準確度，而本文算法的計算精度明顯高于其他兩種方法。

4 結論

（1）矩陣束算法是一種高準確度的信號參數提取方法，本文將其應用到介損角的檢測中，可直接提取基波電壓、電流信號的初始相位，不需要與其他方法配合，且僅需要一個或幾個周期內的采樣值。

（2）電網頻率波動、信號的初始相位不同、諧波分量和直流分量變化、介損角真實值大小、信號的采樣頻率和采樣點數變化對矩陣束檢測方法基本沒有影響。當采樣信號信噪比不小于 25dB時，計算結果完全滿足介損角的檢測準確度要求，不需要對采樣信號進行消噪處理；當采樣信號信噪比小于25dB時，可利用低通濾波器對采樣信號進行簡單預處理，再用矩陣束算法進行檢測。

（3）該方法具有檢測準確度高、穩定性好、速度快、抗噪性能強和簡單易實現的優點，為高壓電容性電氣設備介損角在線檢測提供了一種新的思路。

[1]Natarajian S.Measurement of capacitances and their loss factors[J].IEEE Transactions on Instrumentation and Measurement,1989,38(6): 1083-1087.

[2]Wang P,Raghuveer M R,McDermid W,et al.A digital technique for the online measurement of dissipation factor and capacitance[J].IEEE Transactions on Dielectric Electrical Insulation,2001,8(2):228-232.

[3]李濤,杜曉平,陳瑞林.電容型電流互感器現場試驗 tanδ值異常的分析及解決方法[J].電力系統保護與控制,2009,37(20): 120-122.

Li Tao,Du Xiaoping,Chen Ruilin.Solution to abnormal tanδvalue problem in field test of capacitive current transformer[J].Power System Protection and Control,2009,37(20): 120-122.

[4]王笑棠,李笑倩,金貴,等.一種變頻測量電流互感器介損的方法[J].電力系統保護與控制,2010,38(5): 68-72.

Wang Xiaotang,Li Xiaoqian,Jin Gui,et al.A method of measuring dielectric loss of current transformer by changing frequency[J].Power System Protection and Control,2010,38(5): 68-72.

[5]李濤,杜曉平,劉煥光.電容式電壓互感器自激法的測試及誤差分析[J].電力系統保護與控制,2009,37(5): 31-33.

Li Tao,Du Xiaoping,Liu Huanguang.Discussion about self-excited method error on capacitive voltage transformer[J].Power System Protection and Control,2009,37(5): 31-33.

[6]陳天翔,張保會,陳天濤,等.基于電橋平衡原理的高準確度 tanδ在線測量[J].高電壓技術,2005,31(1): 42-44.

Chen Tianxiang,Zhang Baohui,Chen Tiantao,et al.Research on a new monitoring method of tanδwith low cost and high precision[J].High Voltage Engineering,2005,31(1): 42-44.

[7]蔡國雄,甄為紅,楊曉洪,等.測量介質損耗的數字化過零點電壓比較法[J].電網技術,2002,26(7):15-18.

Cai Guoxiong,Zhen Weihong,Yang Xiaohong,et al.A digitized zero cross point voltage method of comparison for measurement of dielectric losses[J].Power System Technology,2002,26(7): 15-18.

[8]丁暉,申忠如,劉君華.基于小波和相關分析的虛擬介損在線檢測儀[J].高電壓技術,2000,26(4):17-19.

Ding Hui,Shen Zhongru,Liu Junhua.On line measurement of dielectric loss tangent for capacitivetype equipment[J].High Voltage Engineering,2000,26(4): 17-19.

[9]黃晶,顏運昌,胡林.基于小波和改進相關分析的介損測量方法[J].電力系統自動化,2006,30(7):51-54.

Huang Jing,Yan Yunchang,Hu Lin.Dielectric loss measuring based on wavlet analysis and improved correlation function[J].Automation of Electric Power Systems,2006,30(7): 51-54.

[10]王微樂,李福棋,談克雄.測量介質損耗角的高階正弦擬合算法[J].清華大學學報(自然科學版),2001,41(9): 5-8.

Wang Weile,Li Fuqi,Tan Kexiong.Higher-order sine fitting algorithm for dielectric loss measurement[J].Journal of Tsinghua University (Science &Technology),2001,41(9): 5-8.

[11]袁旭龍,馮小華.改進保留非線性算法在介損測量應用中的研究[J].高電壓技術,2005,31(3): 39-40.

Yuan Xulong,Feng Xiaohua.Research of the improved method of nolinear reserved arithmetic applied in the measurement of dielectric loss[J].High Voltage Engineering,2005,31(3): 39-40.

[12]李天云,王靜,郭躍霞,等.基于經驗模態分解和正弦波參數法的介損角測量算法[J].電網技術,2007,31(24): 77-80.

Li Tianyun,Wang Jing,Guo Yuexia,et al.Dielectric loss angle measuring algorithm based on Empirical mode decomposition and sine wave parameter method[J].Power System Technology,2007,31(24): 77-80.

[13]李天云,袁明哲,彭文.EMD在變壓器介質損耗角檢測中的應用[J].中國電力,2011,44(2): 23-26.

Li Tianyun,Yuan Mingzhe,Peng Wen.Measurement of the dielectric loss angle of a transformer by EMD[J].Electric Power,2011,44(2): 23-26.

[14]尚勇,楊敏中,王曉蓉,等.諧波分析法介質損耗因數測量的誤差分析[J].電工技術學報,2002,17(3): 67-71,34.

Shang Yong,Yang Minzhong,Wang Xiaorong,et al.Error analysis for the dielectric loss factor measurement based on harmonic analysis[J].Transactions of China Electrotechnical Society,2002,17(3): 67-71,34.

[15]張介秋,梁昌洪,韓峰巖,等.介質損耗因數的卷積窗加權算法[J].電工技術學報,2005,20(3): 100-104.

Zhang Jieqiu,Liang Changhong,Han Fengyan,et al.Convolution window weighted algorithm for dielectric loss factor[J].Transactions of China Electrotechnical Society,2005,20(3): 100-104.

[16]溫和,滕召勝,曾博,等.基于三角自卷積窗的介損角測量算法及應用[J].電工技術學報,2010,25(7): 192-198.

Wen He,Teng Zhaosheng,Zeng Bo,et al.Dielectric loss angle measurement algorithm and application based on triangular self-convolution window[J].Transactions of China Electrotechnical Society,2010,25(7): 192-198.

[17]Hua Yingbo,Sarkar T K.On SVD for estimating generalized eigen values of singular matrix pencil in noise[J].IEEE Transactions on Signal Processing,1991,39(4): 892-900.

[18]王宇靜,于繼來.電力系統振蕩模態的矩陣束辨識法[J].中國電機工程學報,2007,27(19): 12-17.

Wang Yujing,Yu Jilai.Matrix pencil method of oscillation modes identification in power systems[J].Proceedings of the CSEE,2007,27(19): 12-17.

[19]李天云,袁明哲,蔡國偉,等.基于隨機子空間和最小二乘的介質損耗角檢測方法[J].高電壓技術,2011,37(4): 828-832.

Li Tianyun,Yuan Mingzhe,Cai Guowei,et al.Measurement algorithm of dielectric loss angle based on SSI-LS[J].High Voltage Engineering,2011,37(4):828-832.