轉子動能為外環控制量的永磁同步電動機雙閉環矢量控制策略

王安邦 姜衛東 王群京 佘陽陽

1.合肥工業大學電氣與自動化工程學院 合肥 230009

2.安徽大學電氣工程與自動化學院 合肥 230601）

0 引言

永磁同步電動機因為具備高效率、結構簡單和高功率密度等優點，已被廣泛用于航空航天、數控機床、機器人和電動汽車[1-3]等諸多領域。由于永磁同步電動機具有多變量、非線性及強耦合的特性，故需要采用較為復雜的控制策略。在永磁同步電動機控制系統中，電動機轉速的超調量和調節時間是衡量電動機控制性能的重要指標。目前主要有三種控制方法：變壓變頻控制、磁場定向的矢量控制[4-6]和直接轉矩控制[7-9]，其中矢量控制策略在工業界運用較為廣泛。傳統的矢量控制策略采用轉速、電流雙閉環控制，轉速的階躍響應為典型的二次響應曲線，超調量較大且調節時間較長。

文獻[10]專門對矢量控制和直接轉矩控制進行了比較，直接轉矩控制具有更好的動態特性和更簡單的調制技術，而磁場定向矢量控制的電動機相電流波形質量更好、轉矩脈動更小。隨著電力電子技術、微處理器及現代控制理論的發展，許多學者和專家在矢量控制或直接轉矩控制的基礎上加入了一些算法來提高電動機的響應特性，例如：自適應控制[11,12]、滑模變控制[13,14]和智能控制[15,16]等。

在三相PWM逆變器的控制中，在文獻[17]中將電壓二次方作為反饋構成控制系統的外環，外環輸出的是有功電流給定值，提高了系統的快速性。比較 PWM整流器和永磁同步電動機調速系統，前者是采用電容儲存電場能量，后者是采用轉子慣量（或者折算后的）儲存機械能量，因此這兩種算法具有一定的一致性。在整流器的進一步的研究中，文獻[18]從 Boost變換器的狀態空間平均方程數學模型出發，推導了功率傳遞關系。在此基礎上提出了一種以電流環作為內環、直流側電容儲能環作為外環的反饋控制策略，引入負載功率的前饋，并給出了前饋功率的估計算法，相比較傳統的電壓、電流雙閉環控制策略具有更好的動態特性。

本文提出一種基于轉子動能儲存的矢量控制策略，以轉子動能儲能環作為外環，以電流環作為內環，從能量的角度控制電動機。由電動機的動能儲能關系可知，電動機的儲能與轉速二次方成正比關系，轉速增加，儲能呈二次函數增長。基于轉子動能儲存的矢量控制策略的外環，使用電動機轉子儲存動能的給定值與實際值的差值作為輸入量，輸出量通過解耦得到內環的電流給定值，從而實現對電動機的控制。為了驗證基于轉子儲存動能的矢量控制策略的動態性能，將該策略與傳統的矢量控制策略進行比較。最后還研究了負載變化對系統動態性能的影響。

1 永磁同步電動機的能量交換模型

為了簡化分析，經坐標變換，將永磁同步電動機模型由ABC軸系變換到dq軸系，如圖1所示。

永磁同步電動機在dq軸系下的電壓方程為

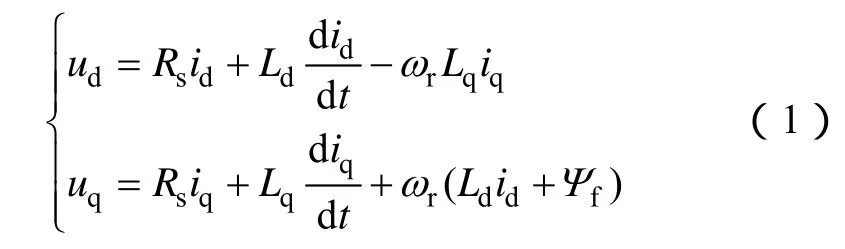
圖1 隱極式永磁同步電動機物理模型Fig.1 Model of non-salient PMSM

式中，Ld為永磁同步電動機的直軸同步電感；Lq為交軸同步電感，隱極式永磁同步電動機Lq=Ld=L；ωr=ωmp0=2 πnp0/60為轉子轉速對應的電角頻率（n為電動機轉速，r/min；ωm為電動機機械角頻率；p0為電動機極對數）；ψf為永磁同步電動機的轉子勵磁磁鏈。為了使電動機轉矩電流比最大且不采用弱磁控制，一般控制使id=0，按照基于轉子磁鏈的定向規則ed=0，且eq=ωrψf。（以下分析中所有帶上標*的量為給定值或估計值，不帶*的量為實際值或反饋值，永磁同步電動機的模型分析中以實際值為依據。）

將式（1）中第一行乘以id加上第二行乘以iq后，得到有功功率的交換關系為

式中，等號左邊為驅動器提供的有功功率。等號右邊第一項為定子電阻消耗的有功功率；第二項為定子電感內磁場儲能增加時所消耗的有功功率，在穩態時磁場儲能不變化，該項為零；第三項為電動機磁阻轉矩所輸出的機械功率，隱極式同步電動機中該項為零；第四項對應于轉子磁鏈轉矩所輸出的機械功率。

將式（1）中第一行乘以iq減去第二行乘以id后，得到無功功率的交換關系為

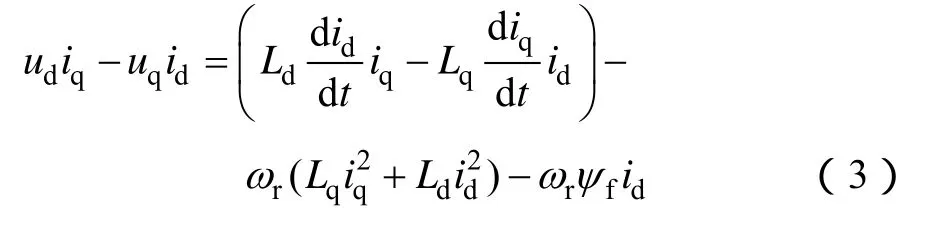
式中，等號左邊為驅動器提供的無功功率。等號右邊第一項為電感內磁場儲能總和變化時所消耗的無功功率，在穩態時該項為零；第二項為電感上消耗的無功功率；第三項為電動機為了實現弱磁調速而吸收的無功功率。

綜合式（2）和式（3）可知在電動機轉矩電流比最大且不采用弱磁控制時，電動機和驅動器之間的能量交換關系為

因為電動機是實現有功交換的工具，所以重點討論由驅動器所提供的有功功率如何轉換為機械功率驅動負載。當忽略掉驅動器的開關器件引起的損耗后，認為永磁同步電動機從驅動器輸入的功率減去電阻、電感儲能損耗后，全部轉換為機械功率輸出。機械功率可以寫為

機械功率Mp的一部分Ap將使電動機轉速增加（也就是使系統所儲存的動能增加），另一部分提供負載消耗功率Lp。電動機從驅動器獲得的q軸電流分量將全部提供電動機內部消耗和輸出的機械功率，電流的d軸分量為無功分量，將其控制設為零。由式（4）和式（5）得

2 以轉子儲存動能作為外環的永磁同步電動機雙閉環矢量控制

基于電動機轉子儲存的永磁同步電動機控制策略采用的雙閉環控制系統中，電動機的轉子所儲存的動能作為反饋量。因為電動機轉子動能儲存與電動機轉子所需要的加速功率構成微分關系，因此電動機轉子動能的實際值與由電動機轉速計算的轉子動能的期望值的差值經過 PI調節器后輸出功率參考值，功率參考值經過與q軸感應電動勢計算后得到電流的q軸分量參考值。

電動機轉子動能外環的輸出的q軸電流分量參考值與實際電流反饋比較后，若無弱磁控制，d軸電流分量參考值為零，兩個軸電流與實際電流反饋比較后，經電流環PI調節器產生dq兩軸的電壓，從而控制永磁同步電動機工作。

2.1 電流內環的設計

永磁同步電動機內環電流控制本質上是控制驅動器輸出電壓與電動機內反電動勢的差值，此差值加在電動機的繞組電阻和電感上，產生電流。

式中,Δud*、Δuq*為加在電動機定子繞組上的用于產生電流的電壓。

為了消除dq軸之間的影響，將電流前饋解耦，解耦后式（7）寫為

考慮電動機轉速可以測量，將式（8）進行拉普拉斯變換，整理后得

此為一階慣性環節，PI調節器的反饋控制規律為

式中，kiP、kiI分別為電流內環比例系數和積分系數；id*、iq*分別為外環產生的無功電流和有功電流給定值。由于d軸和q軸結構相似，以q軸的設計為例對內環進行設計。考慮到電流內環應具有較好的快速性，把內環整定為一階慣性環節，令kiI/kiP=Rs/L，得到

式中，Tc=L/kiI。

最終得到電流內環的控制規律

整個內環的解耦控制策略如圖2所示。

2.2 基于轉子儲存動能反饋的外環設計

圖2 電流內環解耦控制框圖Fig.2 Diagram of the current loop with decoupling

以轉子儲存動能為控制目標的策略，選取電動機儲存的動能EK作為反饋量，通過PI調節器構成控制系統外環。電動機轉子儲存動能與電動機轉速的二次方成正比，控制轉子儲存的動能也可以等效于控制電動機轉速。通過電動機轉速計算出電動機轉子實際存儲的動能，與由給定轉速計算的期望儲能值相比后，經儲能反饋環PI調節器產生電動機加速功率給定p*A，再加上相應的損耗部分和負載估計值，除以電動機的感應電動勢，得到q軸電流給定。由于電動機轉子儲存動能與電動機的加速功率構成微分關系，即

根據反饋控制規律，通過控制電動機的加速功率就可以控制電動機轉子儲存動能，設計該環輸出為加速功率給定電動機轉子儲能環的控制規律為

若將電動機定子電阻所消耗的功率和電感儲能所消耗的功率及負載消耗的功率進行前饋補償以后，可以得到電動機需要從驅動器吸收的總功率pD*

忽略電阻消耗功率和電感儲能吸收的功率（該功率遠遠小于電動機所需的加速功率和負載功率），可以近似認為為了獲得較為準確的加速功率控制，需要將電動機負載功率進行估算和前饋。按照上文定向規則，得到電流內環的q軸電流給定值

基于轉子儲存動能反饋控制策略的框圖如圖3所示，當將損耗功率和負載功率前饋處理后，可寫出閉環傳遞函數為

圖3 控制系統的整體框圖Fig.3 The diagram of the proposed control system

外環按典型Ⅱ型系統設計。給定轉子動能儲能外環中頻帶寬hp，由典型Ⅱ型系統控制器參數整定關系得

一般情況下，可取hp=5代入式（18）得

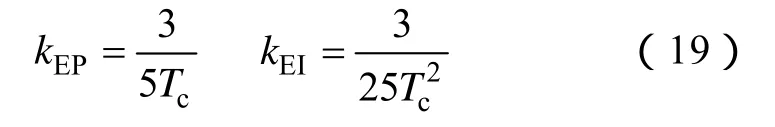
2.3 負載的影響及負載補償

根據式（13）可知，轉子儲存的動能與電動機的轉動慣量、電動機轉速有關。忽略系統的摩擦阻力，考慮到電動機與驅動系統的實際能量交換關系為

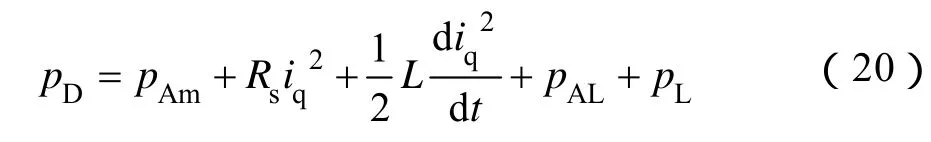
式中，Jm、JL分別為電動機軸和負載轉動慣量；分別為使電動機軸和負載轉速變化時所需要的功率，在負載轉速發生變化時，該項不為零，將pAL+pL考慮為一項pL′。

當電動機負載發生變化時，輸入功率與負載功率不再平衡，由于PI調節器的滯后性，負載首先與電動機轉子動能發生能量交換，引起電動機系統轉速的變化。根據功率表達式，忽略電阻消耗功率和電感儲能吸收的功率，可以寫出負載功率的前饋估計算法。其表達式為

式中，前一項為驅動器輸入的功率；后一項為電動機轉子儲能的變化量。為了消除系統的采樣誤差，采用多周期平均值來估計負載功率，k為平均的周期數。當將負載功率進行前饋補償以后，對永磁同步電動機的控制始終可以等效為對其空載控制，消除了負載波動和轉動慣量變化對系統性能的影響。基于以上分析，得到永磁同步電動機的基于轉子儲能反饋和負載功率前饋的控制策略的框圖如圖3所示。

3 實驗結果及其分析

為了驗證本文所提出算法可行性，將該控制策略與傳統的矢量控制策略進行對比實驗，永磁同步電動機控制系統如圖4所示。測功機為MAGTROL公司的 HD-815-8，示波器為 Aglient公司的 DSO-X 3014A，電動機轉速是由 DSP采集，利用 AD7542數模轉換芯片設計的 DA電路輸出，電流波形由Tektronix公司的A622電流探頭測得。永磁同步電動機的技術參數見下表。

圖4 永磁同步電動機控制系統Fig.4 Control system of PMSM

3.1 傳統雙閉環控制策略和本文所提出控制策略起動時的比較

圖5給出了傳統雙閉環控制策略和本文所提出的控制策略下給定轉速分別為 3 0 0 r/m i n、1 0 0 0 r/m i n和2 0 0 0 r/m i n時，電動機的相電流、q軸電流qi和轉速起動響應曲線。

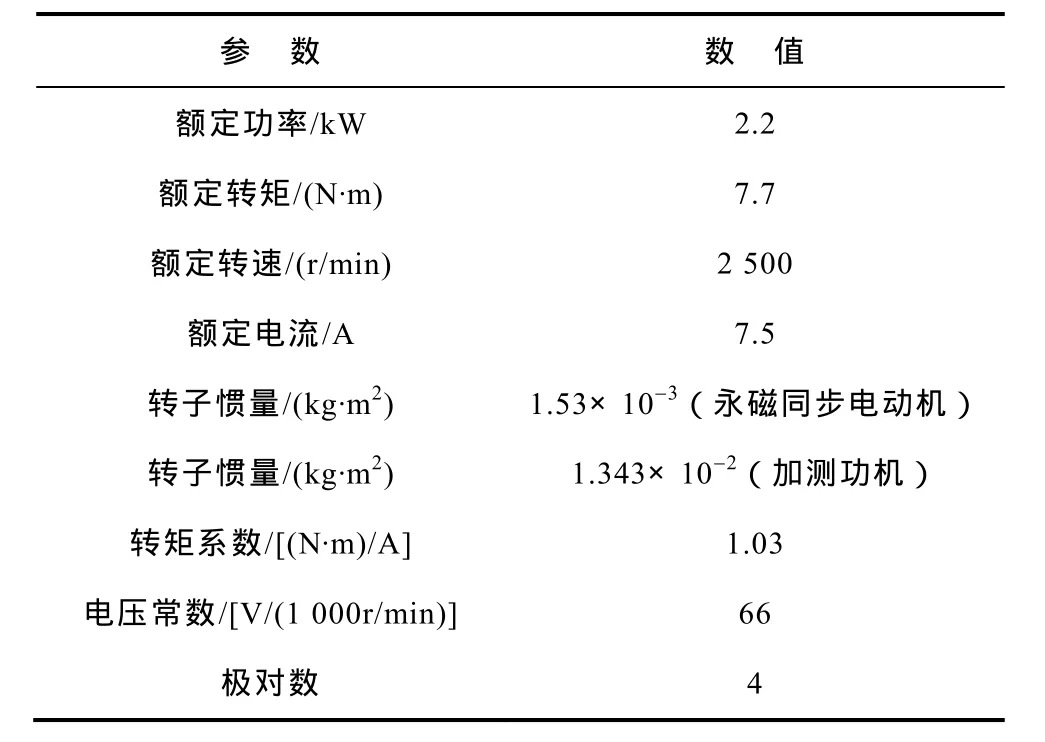
表永磁同步電動機的技術參數Tab.Parameters of PMSM

圖5 電動機起動實驗Fig.5 Experimental results of the startup process

兩種控制策略采用不同的外環調節器，相同的電流內環調節器。比較兩種算法在電動機起動時的響應特性可以看出：

（1）兩種控制策略中，當電動機轉速誤差較大時，轉速外環PI調節器的輸出飽和，電動機以最大電流加速，這一過程中，兩種控制策略表現出一致的加速性能。

（2）當電動機轉速接近設定值時，外環PI調節器中的P調節器開始減小控制比例，而積分調節器開始逐漸增大控制比例，由于本文所提出控制策略在轉速誤差減小時，P調節器以二次方的關系減小，所以在這一過程中本文所提出的控制策略優于傳統的雙閉環控制策略。

（3）當電動機轉速高于設定值時，外環調節器輸出的電流給定會迅速降為零或負值，相比之下本文所提出的控制策略在外環調節器退飽和時優于傳統的雙閉環控制策略。

事實上，兩種控制策略的主要區別在于控制器的外環設計。從q軸電流的曲線看來，本文所提出的控制策略當電動機轉速在設定轉速附近時，q軸電流能夠快速穩定，有效地抑制了電動機的轉速振蕩。與起動過程類似的結論，也可以在電動機轉速給定突減的過程中看出，如圖6所示。

3.2 負載轉矩突變時對負載估算算法的驗證

圖6 電動機減速時實驗結果Fig.6 Experimental results of the deceleration process

圖7 負載轉矩突變時的響應特性Fig.7 Experimental results in the step loadtorque conditions

為驗證本文所提出算法的動態性能，比較了傳統雙閉環控制策略和本文所提出控制策略在負載轉矩突加、突減時的控制性能，實驗結果如圖7所示。制效果。可以看出，當突加負載時，轉速會發生較大的跌落，由于轉速調節器的作用，外環輸出的電流給定加大，電動機輸出更大的轉矩，導致電動機轉速上升，從而恢復到給定轉速。當帶有負載估計算法時，不論是傳統控制策略還是本文所提出的控制策略，突加負載時轉速跌落和突減負載時轉速上升都優于不帶負載估計的控制策略，如圖7c和圖7d所示。這是因為在負載轉矩突變時，首先吸收電動機和負載系統中所儲存的旋轉動能，導致電動機轉速下降，根據式（21），可以估計出負載功率的變化。并將前饋疊加到外環電流給定上，從而實現對功率變化的超前控制。從實驗結果可以看出，帶負載估計的基于轉子動能儲能反饋控制的系統性能為最優。

3.3 轉動慣量變化時負載估計算法的驗證

將電動機脫開負載機，比較不同算法下負載慣量變化對電動機起動響應性能。圖8給出了負載慣量改變，重新起動電動機時，傳統雙閉環控制策略和本文所提出的控制策略分別在帶和不帶負載估計時的響應特性。如圖8a和圖8b所示，當負載轉動慣量改變較大時，未加入負載估計算法，兩種控制策略下，都出現了短時振蕩，在實際系統中必須修改外環PI參數才能消除振蕩。圖8c和圖8d給出了當負載轉動慣量變化較大時，加入負載估計算法，PI參數不做修改情況下的起動波形，兩種控制方法均可以達到圖5類似的起動性能。由此可見，本文所提出的負載估計算法對于負載慣量的變化具有一定的適應性。

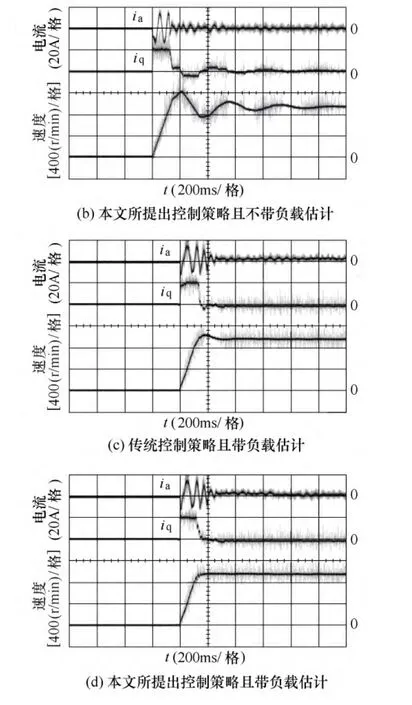
圖8 負載轉動慣量變化情況下響應特性Fig.8 Experimental results under the load rotational inertia varying

4 結論

本文分析了永磁同步電動機的能量交換模型，提出了以電動機轉子儲能作為外環反饋的矢量控制策略。由電動機的動能儲能關系可知，電動機的儲能與轉速二次成正比關系，轉速增加，儲能呈二次函數增長。基于轉子動能儲存的矢量控制策略的外環，使用電動機轉子儲存動能的給定值與實際值的差值作為輸入量，輸出量通過解耦得到內環的電流給定值，從而實現對電動機的控制。即使在相同的轉速增量條件下，初始轉速較大時，電動機需要更多的加速功率，而這一點在轉速、電流雙閉環控制下，因為外環調節器采用轉速的差值作為輸入，是無法實現的；而外環采用動能差值作為調節器輸入，則很好地解決了這一問題。經過理論分析和實驗驗證，本文得到以下結論：

（1）驗證了基于能量反饋的矢量控制策略的可行性。

（2）與傳統的雙閉環矢量控制策略相比，本文所提出的控制策略的動態響應性能更優。

（3）提出了一種負載估計方法，避免了需要根據負載轉矩調節控制器參數的問題，并消除了負載轉動慣量變化對系統性能的影響。

（4）該控制策略的思想同樣適用于其他一些輸出量具有明確的能量函數表達式的系統中，例如PWM整流器的直流側電壓控制等。

[1]韓建群,鄭萍.一種用于電動汽車的永磁同步電機直接轉矩控制的簡化方法[J].電工技術學報,2009,24(1): 76-80.

Han Jianqun,Zheng Ping.A simplified direct torque control method of PMSM applied in electric vehicles[J].Transactions of China Electrotechnical Society,2009,24(1): 76-80.

[2]Estima J O,Marques Cardoso A J.Efficiency analysis of drive train topologies applied to electric/hybrid vehicles[J].IEEE Transactions on Vehicular Technology,2012,61(3): 1021-1031.

[3]李耀華,馬建,劉晶郁,等.電動汽車用永磁同步電機直接轉矩控制電壓矢量選擇策略[J].電機與控制學報,2012,16(4): 43-49.

Li Yaohua,Ma Jian,Liu Jingyu，et al.Voltage vector selection strategy of the DTC for PMSM used in electrical vehicle[J].Electric Machine and Control,2012,16(4): 43-49.

[4]余佩倡,吳峻,周文武.永磁同步電機矢量控制系統設計[J].電力電子技術,2011,45(11): 105-107.

Yu Peichang,Wu Jun,Zhou Wenwu.The design of vector control system of PMSM based on TMS302F28335[J].Power Electronics,2011,45(11): 105-107.

[5]曹瑜,王旭東.一種改進的永磁同步電機矢量控制系統的研究[J].電力電子技術,2012,46(5): 54-56.

Cao Yu,Wang Xudong.Research on an improved PMSM vector control system[J].Power Electronics,2012,46(5): 54-56.

[6]李耀華,吳俊,郭巧娟,等.永磁同步電機矢量控制的兩種實現方法比較[J].微電機,2012,45(1):25-28.

Li Yaohua,Wu Jun,Guo Qiaojuan，et al.Comparison of two ways to implement the FOC for PMSM[J].Micromotor,2012,45(1): 25-28.

[7]Mathapati S,Bocker J.Analytical and offline approach to select optimal hysteresis bands of DTC for PMSM[J].IEEE Transactions on Industrial Electronics,2013,60(3): 885-895.

[8]Xia Changliang,Zhao Jiaxin,Yan Yan,et al.A novel direct torque control of matrix converter-fed pmsm drives using duty cycle control for torque ripple reduction[J].IEEE Transactions on Industrial Electronics,2014,60(6): 2700-2713.

[9]邱鑫,黃文新,楊建飛,等.一種基于轉矩角的永磁同步電機直接轉矩控制[J].電工技術學報,2013,28(3): 56-62.

Qiu Xin,Huang Wenxin,Yang Jianfei,et al.A direct torque control strategy based on torque angle for permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society,2013,28(3):56-62.

[10]Aguirre M,Calleja C,Lopez-de-Heredia A,et al.FOC and DTC comparison in PMSM for railway traction application[C].Proceedings of the Power Electronics and Applications 2011: 1-10.

[11]Jin H Z,Lee J M.An RMRAC current regulator for permanent magnet synchronous motor based on statistical model interpretation[J].IEEE Transactions on Industrial Electronics,2009,56(1): 169-177.

[12]黃科元,周滔滔,黃守道,等.永磁伺服系統基于微分自適應補償的陜速無超調控制策略[J].電工技術學報,2014,29(9): 138-144.

Huang Keyuan,Zhou Taotao,Huang Shoudao,et al.Overshoot and fast response control of PMSM servo system based on differential adaptive compensation[J].Transactions of China Electrotechnical Society,2014,29(9): 138-144.

[13]Corradini M L,Ippoliti G,Longhiss,et al.A quasi-sliding mode approach for robust control and speed estimation of PM synchronous motors[J].IEEE Transactions on Industrial Electronics,2012,59(2):1096-1104.

[14]Zhang Xiaoguang,Sun Lizhi,Zhao Ke,et al.Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation techniques[J].IEEE Transactions on Power Electronics,2013,28(3): 1358-1365.

[15]Lin F J,Hung Y C,Hwang J C,et al.Fault-tolerant control of a six-phase motor drive system using a takagi-sugeno-kang type fuzzy neural network with asymmetric membership function[J].IEEE Transactions on Power Electronics,2013,28(7): 3557-3572.

[16]Han H C,Jung J W.Discrete-time fuzzy speed regulator design for pm synchronous motor[J].IEEE Transactions on Industrial Electronics,2013,60(2):600-607.

[17]王恩德,黃聲華.三相電壓型 PWM 整流器的新型雙閉環控制策略[J].中國電機工程學報,2012,32(15): 24-30.

Wang Ende,Huang Shenghua.A novel double closed loops control of the three-phase voltage-sourced PWM rectifier[J].Proceedings of the CSEE,2012,32(15): 24-30.

[18]姜衛東,吳志清,胡楊.直流電容儲能反饋和負載功率前饋的Boost變換器控制策略[J].電力自動化設備,2014,34(8): 103-107.

Jiang Weidong，Wu Zhiqing，Hu Yang.Control strategy based on DC-link capacitor energy feedback and load power feedforward of Boost converter[J].Electric Power Automation Equipment,2014,34(8):103-107.