基于線性化Poincaré映射模型的非線性電力電子系統控制方法

王 剛 侍喬明 付立軍 紀 鋒 陳宇航 蔣文韜

1.海軍工程大學艦船綜合電力技術國防科技重點實驗室 武漢 430033

2.西安交通大學電氣工程學院 西安 710049

0 引言

隨著能源、交通、國防和生活等領域應用需求的提升和現代科學技術的進步，各種復雜電力電子變流裝置的應用越來越廣泛，成為獨立電力系統的核心電能變換單元[1,2]。構建獨立供電的非線性電力電子系統時，良好的動態性能是保證系統安全穩定運行的前提條件。動態性能指標與系統拓撲結構、元器件參數、運行方式和控制方式有關。一般說來，提高系統動態性能指標最有效和最經濟的方法是采用先進的控制方法[3]。

系統控制的基礎是系統動態性能分析。非線性電力電子系統有三種非線性來源：不同階段系統拓撲結構的切換，占空比控制方法和非線性元件[4,5]。上述三種非線性因素互相耦合，無法解耦處理。陸用電力系統的穩態是平衡點，動態性能是平衡點附近的動態響應，將描述系統的非線性微分方程在平衡點線性化，對其進行特征結構分析，即可得到系統動態響應的模式和模態等信息。非線性電力電子系統的穩態是周期軌道，動態性能是周期軌道的動態響應，Poincaré映射反映的是其采樣時刻離散狀態變量的動態響應，而一個周期內狀態變量的動態響應取決于系統的非線性微分方程。這種復雜的時變非線性特性使得非線性電力電子系統的動態性能分析比較困難，同時系統呈現出分叉和混沌等豐富的動力系統特征[4]。非線性電力電子系統的動態性能分析方法有三種：狀態空間平均法、數值仿真法和Poincaré映射法。

狀態空間平均法通過對各個開關工作模態做平均處理，得到變換器的近似解析模型[6,7]。這種轉換是近似的，其準確度隨著系統工作頻率與開關頻率比值的增大而降低。某些情況下即使開關頻率很高，狀態空間平均法仍有較大的誤差，這影響了其動態性能分析的有效性和準確性[7]。

數值仿真法將非線性電力電子系統用時變非線性微分方程描述，針對特定的擾動，利用時域仿真計算系統變量完整的時域響應[8]。其缺點是：擾動和時域響應觀測量的選擇對結果影響很大，仿真計算耗時太多，物理概念不清晰，難以利用仿真結果找出影響動態性能的主要因素和設計系統的控制策略[9]。

Poincaré映射法將周期軌道的漸近穩定性等效為平衡點的Lyapunov穩定性，這種等效是嚴格的。利用周期軌道Poincaré映射可以研究系統的動態性能[4,5]。目前這種方法用于系統動態特性分析的較多，有助于理解系統中復雜的動力系統行為，但對于解決系統設計問題的指導作用有限[10,11]。因而迫切需要研究基于Poincaré映射的非線性電力電子系統控制方法。

文獻[5]針對系統的三種非線性，提出了基于梯形積分法的周期軌道及其 Poincaré映射算法。文獻[5，12]提出了采用1與 Poincaré映射 Jacobian矩陣譜半徑的差作為系統的穩定裕度指標，該指標不僅能反映系統的穩定水平，還可以反映系統狀態變量增量動態響應的衰減速度。

本文構造包含控制變量作用的周期軌道Poincaré映射，用線性化 Poincaré映射模型表示非線性電力電子系統狀態變量的動態響應，以系統穩定裕度指標為目標優化控制參數，建立基于線性化Poincaré映射模型的非線性電力電子系統控制方法。

1 基于線性化Poincaré映射模型的控制

包含三種非線性來源的非線性電力電子系統模型為[5]

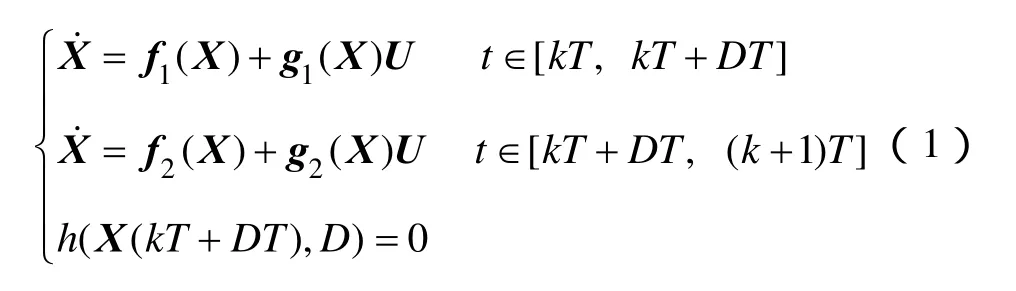
式中，T為開關周期；D為占空比；狀態變量X為m維；控制變量U是周期為T的函數，即 ( ) ()UU。

首先確定系統（1）的周期軌道。假設狀態變量在周期軌道上運行，在開關周期初始時刻kT的狀態變量為X0。在開關周期第1階段取n1個分點，第2階段取n2個分點，令n=n1+n2，設每個分點的狀態變量為X0,X1,…,Xn，控制變量為U0,U1,…,Un。用隱式梯形積分公式列寫周期軌道滿足的方程為

式中，未知數為X0,X1,…,Xn,D，其個數為m(n+1)+1個，方程數也是m(n+1)+1個。式（2）的初值可由狀態空間平均法提供，利用Newton Raphson法求解該方程，即可得到系統的周期軌道。

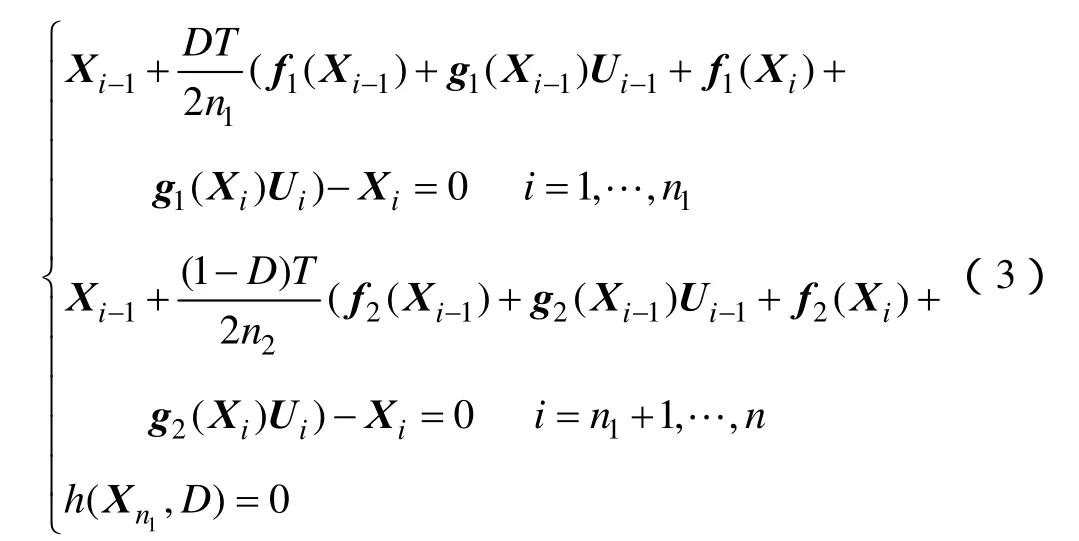
式（3）是關于變量 （X0,X1,…,Xn,D）T(m(n+1)+1維)的mn+1 個方程，給定一個X0,U0,··,Un，就對應一個Xn，即確定了隱函數形式的Poincaré映射

假設系統的控制規律為

設 Poincaré映射采樣時刻為開關周期開始時刻，其狀態變量用上標表示，以示與一個周期內狀態變量分點的區別，分別為X0,…,Xn。聯立式（3）和式（5），可得開關周期開始時刻狀態變量的Poincaré映射為

用Δ表示相應變量的增量，在Poincaré映射采樣時刻周期軌道相應的狀態點Xe處，對式（6）進行線性化得

式（7）即為系統的線性化Poincaré映射模型，它包含系統控制變量的影響，將周期軌道的動態響應特性變換為平衡點為Xe的線性化動態響應特性（式（7））。注意這種變換僅是對Poincaré映射采樣時刻狀態變量動態響應的線性近似，并不對應所有時刻狀態變量的動態響應。如果采樣時刻的狀態變量達到Xe，那么系統的狀態變量一定進入周期軌道，因此線性化 Poincaré映射模型可以表示周期軌道的動態響應特性。

上述系統的穩定裕度為

式中，()ρA為矩陣A特征值的最大模，即A的譜半徑。

系統穩定裕度不僅是系統穩定的裕度指標，而且是狀態變量擾動量衰減速度的量度。其值越大，系統穩定裕度越大，狀態變量擾動量的衰減越快[5,12]，系統動態性能越好。基于此，采用該指標作為系統控制性能的評價指標。

作為采用周期軌道模型控制的初步研究，假設系統控制規律（5）的函數形式已知，但相關控制系數有待確定。例如，系統的控制規律為狀態反饋或PI控制。這時對于一組向量形式為K的給定控制系數，其控制性能指標Sm即可確定。對于這組系數進行優化以得到系統最大的控制性能指標Sm，這樣就得到了基于線性化Poincaré映射模型的系統控制規律。

本文主要討論基于周期軌道模型的系統控制設計方法，采用依次優化算法確定系統的控制規律，也可以采用其他優化算法。依次優化算法為：不斷改變控制系數向量K的第一個分量，其他分量不變，計算系統控制性能指標Sm，使這一指標最大，從而確定K的這個分量。同理依次確定K的其他分量。再重復上述過程，直到相鄰兩次K差值的范數小于給定值。

2 斬波器占空比設計

采用文獻[5]的帶有恒功率負載的Boost閉環控制系統，除了恒功率負載的功率P=1.5W，其余電路參數不變，如圖1所示。

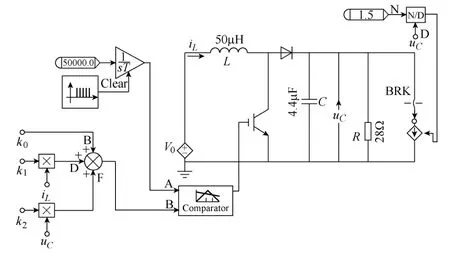
圖1 Boost電路圖Fig.1 Circuit diagram of Boost

電路參數如下：R=28Ω，C=4.4μF，L=50μH，開關管的導通電阻RT=0.005Ω，二級管的導通電阻Rd=0.01Ω，恒功率負載的功率P=1.5W，電源電壓V0=5V，f=50kHz。設iL和uC分別為電感電流和電容電壓，假定系統的占空比反饋控制規律采用狀態變量反饋控制，優化其控制參數，即

設系統初始控制參數對應的占空比方程為

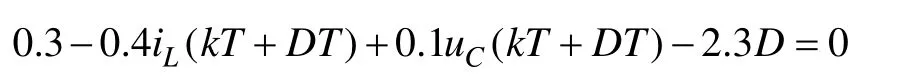
取n1=2，n2=8，周期軌道對應的占空比De為0.253 8，其周期軌道如圖2所示。

圖2 Boost電路周期軌道Fig.2 Periodic orbit of Boost

利用前述算法可以計算系統周期軌道 Poincaré映射的 Jacobian矩陣N，Poincaré映射抽樣時刻狀態變量的微分增量對于占空比增量ΔD的 Jacobian矩陣L，則 Poincaré映射時刻狀態變量的微分增量有下列關系

設系統增量形式的反饋控制為

式中，K為待定的行向量，1nΔX為系統狀態切換時的狀態變量增量。

同理對應于拓撲切換時的狀態變量1nΔX進行微分增量計算，可得

綜合式（9）～式（11），有

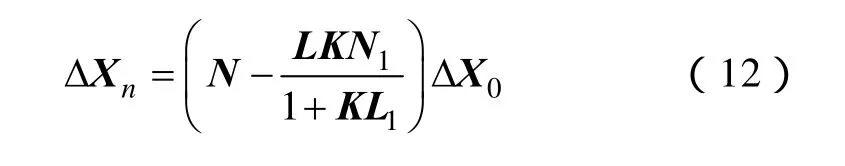
采用依次優化算法計算向量K，表1是本文設計方法的結果，可見采用設計控制參數，系統穩定裕度和動態響應速度有了顯著提高。假定在 0.03s時電源電壓V0跌落 10%，變為 4.5V。圖3是用PSCAD仿真計算的Boost電路在初始控制參數和設計控制參數情況下的動態響應比較，仿真步長為0.1μs。可見采用設計控制參數，系統動態響應性能在穩態偏移、響應速度和超調量等方面都有顯著的提高。

表1 Boost電路占空比設計結果Tab.1 Design results of duty ratio of Boost

圖3 Boost電路狀態變量動態響應Fig.3 Dynamic response of state variables of Boost

圖4是采用初始控制參數和設計控制參數，Boost電路狀態變量動態響應及其線性化 Poincaré映射模型相應結果的比較。其中實線為狀態變量動態響應，由式（2）和式（3）計算；虛線為線性化Poincaré映射模型的動態響應，由式（7）計算。系統狀態變量的動態響應與圖3一致，線性化Poincaré映射模型的狀態變量動態響應可表征其映射采樣時刻狀態變量的動態響應。

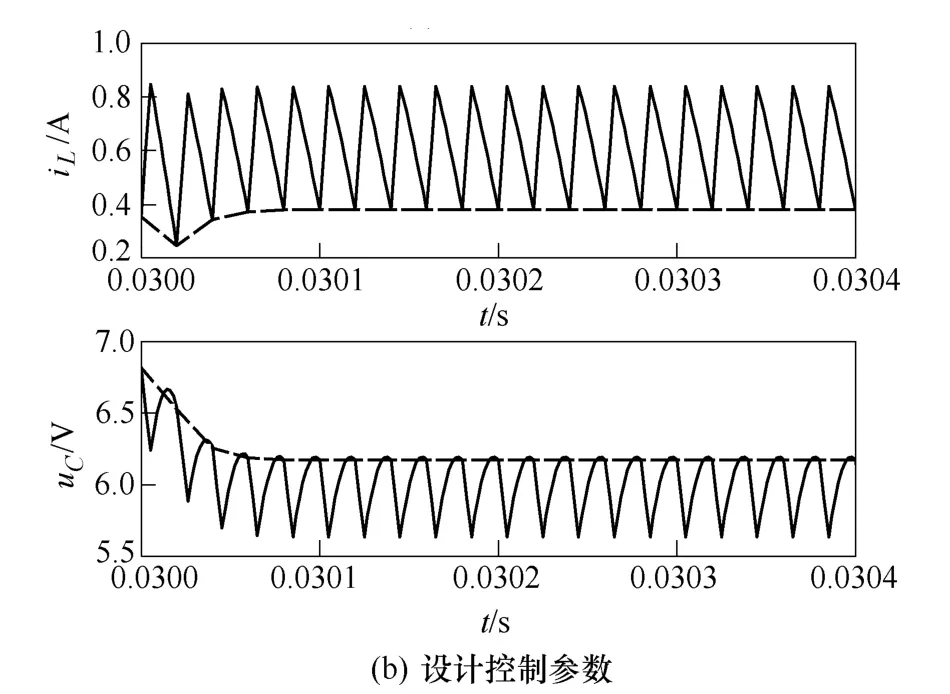
圖4 Boost線性化Poincaré映射模型狀態變量動態響應Fig.4 Dynamic response of state variables of Boost by linearized Poincaré mapping model

3 不控整流發電機的勵磁設計

采用文獻[13]的帶恒功率負載的不控整流發電機系統，除了恒功率負載的功率P=1.5kW，其余電路參數不變，如圖5所示，系統參數見表2。

圖5 發電機不控整流系統Fig.5 Diode rectifiers-generator system

發電機勵磁采用PI控制，維持其整流輸出電壓udc為額定值ur=500V，如圖6所示。優化其比例環節和積分環節的增益系數k1和k2。

圖6 發電機不控整流系統勵磁控制Fig.6 Excitation control of diode rectifiersgenerator system

表2 發電機不控整流系統參數[13]Tab.2 Parameters of diode rectifiers-generator system

假定零時刻為從VD1和VD6的導通階段剛好進入VD1、VD2和VD6的換向階段，這時同步發電機的轉子位置為θ1，則系統的狀態變量為其中id為定子d軸電流，iq為定子q軸電流，ifd為勵磁繞組電流，ikd為d軸阻尼繞組電流，ikq為q軸阻尼繞組電流。

首先根據直流電壓額定值確定發電機勵磁電動勢Ef的額定值Efe。給定一個勵磁電動勢，計算系統周期軌道，再計算直流電壓的周期平均值。不斷調整勵磁電動勢，直到該周期平均值為其額定值。這樣就得到了勵磁電動勢的額定值Efe=1.01。

給定的一個Ef，系統周期軌道Poincaré映射為[13]

式中，X1和X2分別為周期起始時刻和下一個周期起始時刻的狀態變量。

假定開關周期初始時刻狀態變量的擾動為ΔX1，發電機勵磁電動勢的擾動為ΔEf，則下一個開關周期初始時刻狀態變量的擾動ΔX2為

式中，M和L矩陣可由式（14）進行偏微分運算得到。勵磁控制的模型為

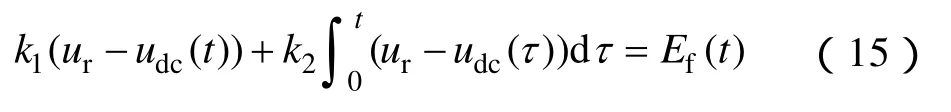
發電機不控整流系統的周期T0=1/(6fs)，fs為發電機的額定頻率。假定在mT0時刻研究系統處于周期軌道上，這時的直流電壓為ue，則有

下一個周期(m+1)T0時刻，有

上述兩式相減得

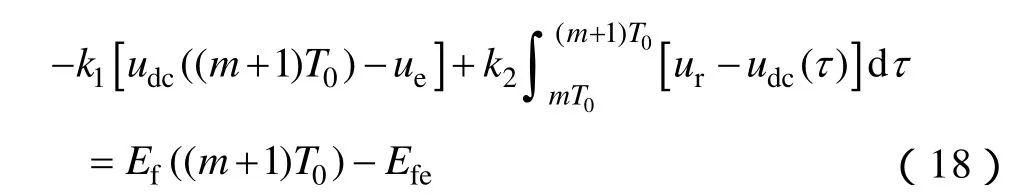
式（18）表示在[mT0,(m+1)T0]這個周期內直流電壓擾動對于發電機勵磁電動勢Ef的影響。由于系統周期T0很小，采用梯形積分公式計算上式的積分

經過一個周期T0，發電機勵磁電動勢增量與狀態變量增量的關系以矩陣形式表示為

式中

聯立式（14）和式（20），可得基于線性化Poincaré映射模型的不控整流發電機勵磁控制模型為

式中，E為單位矩陣。

式（2）表明勵磁控制性能指標為Sm=1-ρ((E-LN)-1(M+LN))，采用依次優化算法即可21得到k1和k2的優化值。

給定兩組初始勵磁控制參數k1和k2，第一組為0.008 7和 0.087，第二組為 0.007和 0.07，系統穩定裕度指標Sm分別為-0.002和0.000 1，這時系統處于臨界穩定的邊界。利用依次優化算法計算的勵磁控制參數k1和k2為 0.000 7和0.049，系統穩定裕度指標Sm為0.008 8，可見系統的穩定裕度和控制性能有了較大提升。

為了驗證勵磁控制對于系統狀態變量動態響應的影響，假定系統帶 1 364W的恒功率負荷進入穩態，在 15s時負荷忽然增加 10%（136W），達到1.5kW。采用PSCAD仿真軟件計算上述三組勵磁控制參數的直流電壓動態響應如圖7所示，仿真步長為10μs。可見采用設計控制參數，系統直流電壓的動態響應性能在振蕩幅度、超調量和響應速度等方面都有了顯著的提高。

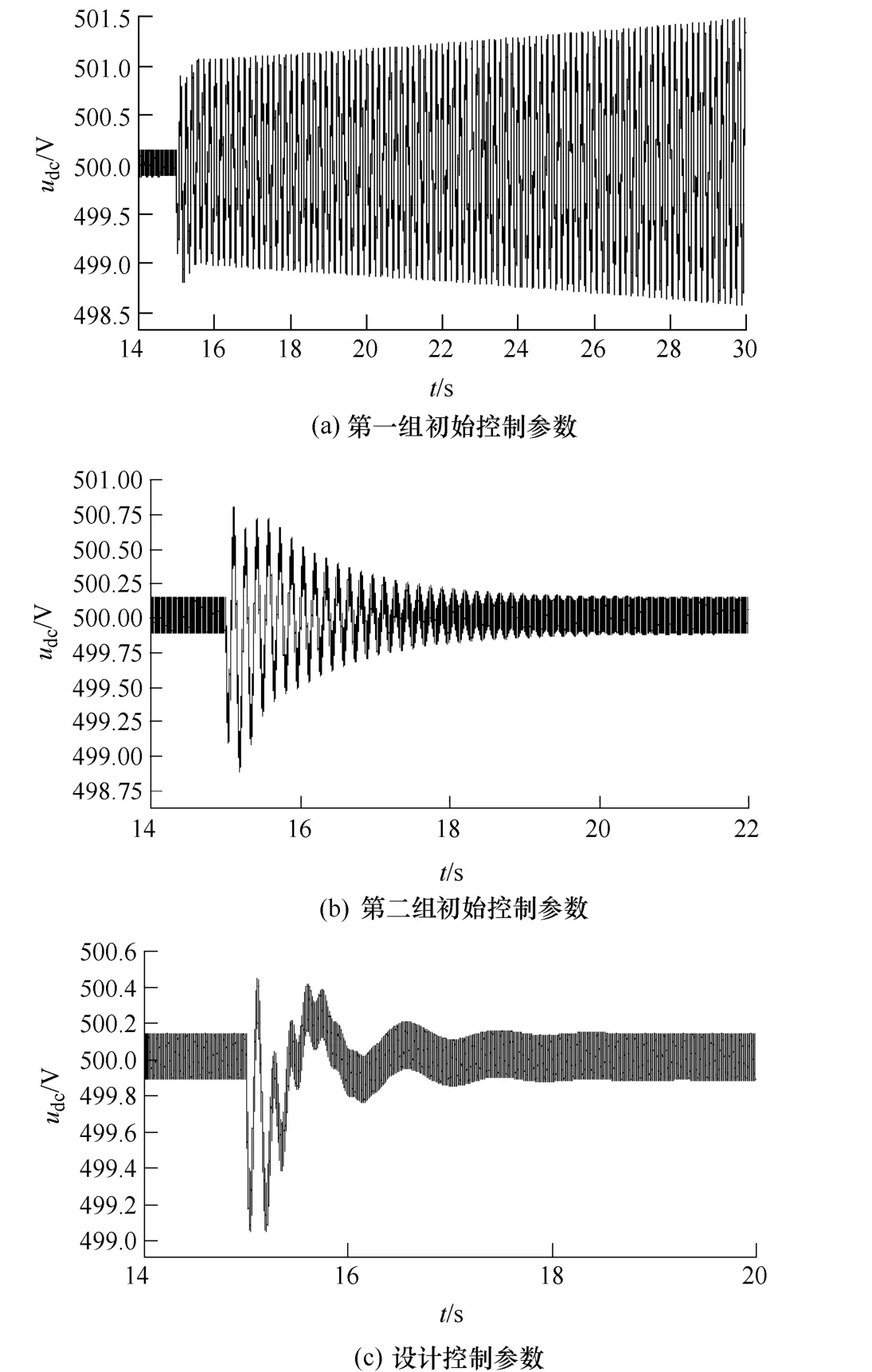
圖7 發電機不控整流系統直流電壓的動態響應Fig.7 Dynamic response of DC voltage of diode rectifiers-generator system

綜合上述，基于線性化 Poincaré映射模型的非線性電力電子系統控制規律的設計流程如下：

（1）建立系統的周期軌道模型，根據控制要求，確定系統穩態時的控制變量和周期軌道，驗證系統穩態性能指標符合要求。

（2）設系統控制規律對應的控制系數向量為K，建立系統周期軌道的Poincaré映射和系統的控制方程，對其進行線性化，得到相應的矩陣，推導系統的控制性能指標Sm的表達式。

（3）以性能指標Sm最大為目標，采用依次優化算法確定系統的優化控制系數向量K。

（4）考慮處于周期穩態的系統遭受小擾動，采用時域仿真方法，檢驗系統的動態響應是否符合要求。

4 結論

考慮控制變量擾動和Poincaré映射采樣時刻系統狀態變量擾動對于下一個采樣時刻狀態變量的影響，本文利用梯形積分法建立了包含控制變量作用的周期軌道Poincaré映射，對此進行線性化就得到了非線性電力電子系統的線性化 Poincaré映射模型，它可以表示系統狀態變量的動態響應。基于該模型，以系統穩定裕度指標最大為目標，采用依次優化算法確定系統的控制參數，從而建立了基于線性化 Poincaré映射模型的非線性電力電子系統控制方法。

理論分析和仿真試驗表明，本文提出的控制方法能夠有效地提高非線性電力電子系統的動態響應性能，為系統控制設計提供了一條新的途徑。

[1]Ma Weiming.The integrated power system in warship[C].Proceedings of the 5th International Marine Electrotechnology Conference,Shanghai,China,September 2003,1: 2-7.

[2]陳明,汪光森,馬偉明.多重化雙向DC-DC變換器PI滑模變結構控制策略研究[J].電力自動化設備,2008,28(4): 53-57.

Chen Ming,Wang Guangsen,Ma Weiming.PI sliding mode control strategy for multi-channel interleaved bi-directioal DC-DC converter[J].Electric Power Automation Equipment,2008,28(4): 53-57.

[3]盧強,梅生偉,孫元章.電力系統非線性控制[M].北京: 清華大學出版社,2008.

[4]Soumitro Banerjee,George C Verghese.Nonlinear phenomena in power electronics[M].New York:IEEE Press,2001.

[5]王剛,范學鑫,付立軍,等.采用周期軌 Poincaré映射的非線性電力電子系統小干擾穩定性分析[J].中國電機工程學報,2012,32(1): 84-92.

Wang Gang,Fan Xuexin,Fu Lijun,et al.Small signal stability analysis of nonlinear power electronic systems based on Poincaré mapping of the periodic orbit[J].Proceedings of the CSEE,2012,32(1): 84-92.

[6]Middlebrook R D,Cuk S.A general unified approach to modeling switching-converter power stages[C].IEEE Power Electrical Systems Conference,NewYork,1976: 23-25.

[7]Brand L,Bass R M.Extension of averaging theory for power electronics systems[J].IEEE Transactions on Power Electronics,1996,11(4): 542-553.

[8]Shortt D J,Lee F C.Improved switching converter model using averaging and discrete techniques[J].IEEE Transactions on Aerospace and Electronic Systems,1983,19(2): 190-202.

[9]倪以信,陳壽孫,張寶霖.動態電力系統的理論和分析[M].北京: 清華大學出版社,2002.

[10]Banerjee S.Bifurcations in two-dimensional piecewise smooth maps-theory and applications in switching circuits[J].IEEE Transactions on Circuits and Systems-1: Fundamental Theory and Applications,2000,47(5): 3100-3113.

[11]馬西奎,李明,戴棟,等.電力電子電路與系統中的復雜行為研究綜述[J].電工技術學報,2006,21(12): 1-11.

Ma Xikui,Li Ming,Dai Dong,et al.Reviews of research on complex behavior of power electronic circuits and systems[J].Transactions of China Electrotechnical Society,2006,21(12): 1-11.

[12]王剛,紀鋒,謝楨,等.基于周期軌模型的綜合電力系統逆變器性能分析[J].中國電機工程學報,2012,32(增刊): 210-216.

Wang Gang,Ji Feng,Xie Zhen,et al.Inverter performance analysis of integrated power system based on periodic orbit model[J].Proceedings of the CSEE,2012,32(Sup.): 210-216.

[13]Wang Gang,Fu Lijun,Fan Xuexin,et al.Periodic orbit model of diode rectifiers-synchronous machine system[J].Science China Technological Sciences,2013,56(1): 245-252.