基于雙曲正切函數的變步長凸組合最小均方誤差算法

陳立偉， 譚志良， 崔立東

(軍械工程學院靜電與電磁防護研究所， 河北 石家莊 050003)

基于雙曲正切函數的變步長凸組合最小均方誤差算法

陳立偉， 譚志良， 崔立東

(軍械工程學院靜電與電磁防護研究所， 河北 石家莊 050003)

利用雙曲正切函數對凸組合最小均方(Convex Combination of Least Mean Square, CLMS) 算法進行了改進，提出了Th-VSCLMS(Tanh Variable Step Convex Combined Least Mean Square)算法。理論分析表明：改進算法的性能優于普通的變步長算法。在不同信噪比下對VSLMS(Variable Step Least Mean Square)、CLMS、Th-VSCLMS算法進行了仿真對比分析，結果表明：Th-VSCLMS算法的收斂性、穩態性、抗擾動性、低信噪比的濾波效果、計算量均得到較好的改善，且其凸組合濾波結構優于單一濾波結構。

凸組合最小均方算法；雙曲正切函數；擬合系數

最小均方(Least Mean Square，LMS)算法由Widrow和Hoff提出[1]，其收斂速度與步長成正比，穩態誤差與步長成反比[2]。現有固定步長的LMS算法很難同時獲得初始收斂速度與穩態誤差均良好的性能，為解決二者的矛盾，許多變步長算法先后被提出，其中最具代表性的算法有：歸一化最小均方(Normalized Least Mean Square,NLMS)算法[3]、改進的Sigmoid函數變步長LMS(Sigmoid Variable Step-size of Least Mean Square,SVSLMS)算法[4]、指數因子變步長LMS算法[5]等。變步長LMS算法雖然通過對算法步長的折中，使收斂速度和穩態誤差基本都能滿足實際應用的要求，但其對2種性能都有限制，因而也抑制了自適應濾波器處理信號的性能。

近幾年，利用并行計算思想提出了凸組合最小均方(Convex Combination of Least Mean Square,CLMS)濾波器算法[6]。該算法將2個不同迭代步長的最小均方算法濾波器并聯起來，其中：一個濾波器提高算法的收斂速度；另一個濾波器保證穩態性能。于霞等[7]提出了一種變步長凸組合最小均方(Variable Step-size Convex Combination of Least Mean Square,VSCLMS)濾波器算法，其利用變步長調整原則，將其中1個固定步長LMS算法濾波器改為變步長LMS(Variable Step-size of Least Mean Square, VSLMS)算法濾波器，該濾波器在收斂速度、跟蹤性能、系統失調性等方面都有較大提高。本文利用雙曲正切函數(Hyperbolic Tangen Function，Tanh)，作為其中快速LMS算法的步長函數來提高算法的收斂速度與穩態性，提出了Th-VSCLMS算法并通過仿真分析驗證其性能。

1 VSCLMS算法

VACLMS算法濾波器原理[6]如圖1所示。其中：wi(n)、yi(n)、ei(n)(i=1,2)分別為LMS濾波器的權重、輸出和誤差；λ(n)、yeq(n)、eeq(n)分別為VSCLMS濾波器的聯合系數、輸出和誤差；u(n)為輸入；d(n)為期望輸入。

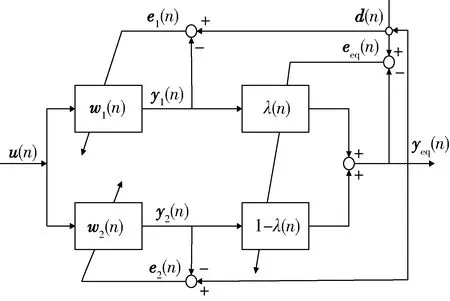
圖1 VSCLMS算法濾波器的原理

變步長凸組合自適應濾波器克服了單一濾波器存在的不足，其采用2套完整的濾波器對信號進行處理，通過1個聯合系數λ(n)來控制2個濾波器在整個濾波過程發揮作用的比例，使其在提高收斂速度或降低穩態誤差時不降低另一方面的性能。

VSCLMS算法濾波器的等價權向量為

w(n)=λ(n)w1(n)+[1-λ(n)]w2(n)，

(1)

式中：λ(n)∈[0,1],

λ(n)=sgm[a(n)]=1/(1+e-a(n)),

(2)

其中，

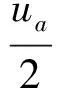
a(n-1)+uaeeq(n-1)[e2(n-1)-e1(n-1)]×

λ(n-1)[1-λ(n-1)],

(3)

為以最小均方誤差為準則進行自適應的函數，符合LMS理論的魯棒性[7]。式(3)中,ua為綜合步長。

輸出為

yeq(n)=λ(n)y1(n)+[1-λ(n)]y2(n)。

(4)

誤差為

eeq(n)=λ(n)e1(n)+[1-λ(n)]e2(n)=

λ(n)[d(n)-w1(n)uT(n)]+

[1-λ(n)][d(n)-w2(n)uT(n)]=

d(n)-w(n)uT(n),

(5)

式中:

ei(n)=d(n)-wi(n)uT(n),i=1,2。

(6)

由算法的結構與原理可得：在收斂初始階段，應利用較大步長的VSLMS濾波器(λ≈1，weq≈w1)；收斂到穩定階段時，則利用較小步長的VSLMS濾波器，以確保誤差更小(λ≈0，weq≈w2)。

2 Th-VSCLMS算法分析

2.1 凸組合濾波器結構的優越性

通常采用額外均方誤差(Excess Mean Square Error, EMSE)來衡量濾波器的性能，并將其定義為濾波器在工作過程中除最小均方誤差外的額外誤差項。為便于分析凸組合算法優于其中任何單獨的LMS算法，假設學習迭代次數n取其極限值∞，由于e(n)=ea(n)+e0(n),其中:ea(n)為先驗誤差;e0(n)為獨立建模觀測噪聲[8]。則根據EMSE計算公式

(7)

(8)

可得各濾波器的EMSE。

定義基于ea(n)的綜合EMSE為

(9)

由式(9)與Cauchy-Schwartz不等式可得：濾波器的綜合EMSE不會同時高于單個濾波器的EMSE，即

Jex，1,2(∞)≤max{Jex，1(∞),Jex，2(∞)}。

(10)

由上述分析可知：凸組合自適應濾波器的EMSE優于組合中任何單一自適應濾波器的EMSE。

2.2 TH-VSCLMS算法

本文提出以Tanh為變步長自適應濾波器的步長因子，另一個為固定步長的自適應濾波器。TH-VSCLMS算法可表示為

u(n)=βtanh(α|e(n)|γ),

(11)

式中：β為控制步長函數的范圍；α為控制步長函數的形狀；γ為控制步長函數在誤差接近0時底端的平滑程度。

圖2為tanh函數與Sigmoid函數的擬合曲線。Sigmoid函數是變步長LMS算法中步長函數的標準，大部分變步長函數均基于此函數得來。

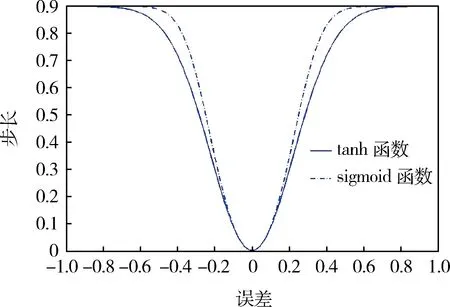
圖2 tanh函數與Sigmoid函數的擬合曲線

由圖2可知：tanh函數符合變步長函數的變化準則，即步長隨誤差的變化而變化。在收斂的初始階段，濾波器要求較快的收斂性能，此時可將β設置為允許范圍內的最大值(β≤1/λmax)；在收斂穩態階段，步長逐漸變小，保證了較小的穩態誤差，但在穩態階段，由于被污染的噪聲容易造成步長的波動，使算法的穩態性能下降，可利用CLMS濾波器的另一個固定步長的LMS算法來減小穩態性能的損失。

2.3 復雜度分析

從公式的復雜度分析可看出：與CLMS算法、VSLMS算法相比，Th-VSCLMS算法的計算量有相應增加，特別是與傳統的VSLMS算法相比，增加更多；較大的計算量對其硬件實現提出了更高要求。但綜合分析來看：Th-VSCLMS算法收斂速度較快，從而減小了算法的計算量，且快速的收斂性在許多情況下非常重要，如軍用雷達需要在較短的時間內發現和跟蹤目標；另外，該算法的凸組合結構有較好的抗干擾能力，能更好地保證通信信號的質量。

3 仿真分析

將Th-VSCLMS算法、CLMS算法、VSLMS算法用于干擾抵消仿真中，進一步驗證Th-VSCLMS算法的性能。通過200次獨立仿真并求其平均值。為了客觀對比3種算法的收斂性與跟蹤性能，設Th-VSCLMS算法的參數值為：β=3，α=500，u2=0.01,ua=20。CLMS算法、VSLMS算法的參數取值引用文獻[6]中的參數值：VSLMS算法中，α=300,β=0.05；CLMS算法中，u1=0.1,u2=0.05,ua=20。

3.1 抗干擾性能仿真

設濾波器階數為8；期望信號為正弦信號S(s=sin(0.01πt))與高斯白噪聲U(均值為0，方差為0.1)的疊加；參考輸入信號為與U成比例函數的高斯白噪聲V,設相應信噪比SNR=10。為了更好地比較算法的跟蹤性能，設迭代到1 500次時權值突變，得出如圖3所示的收斂曲線。

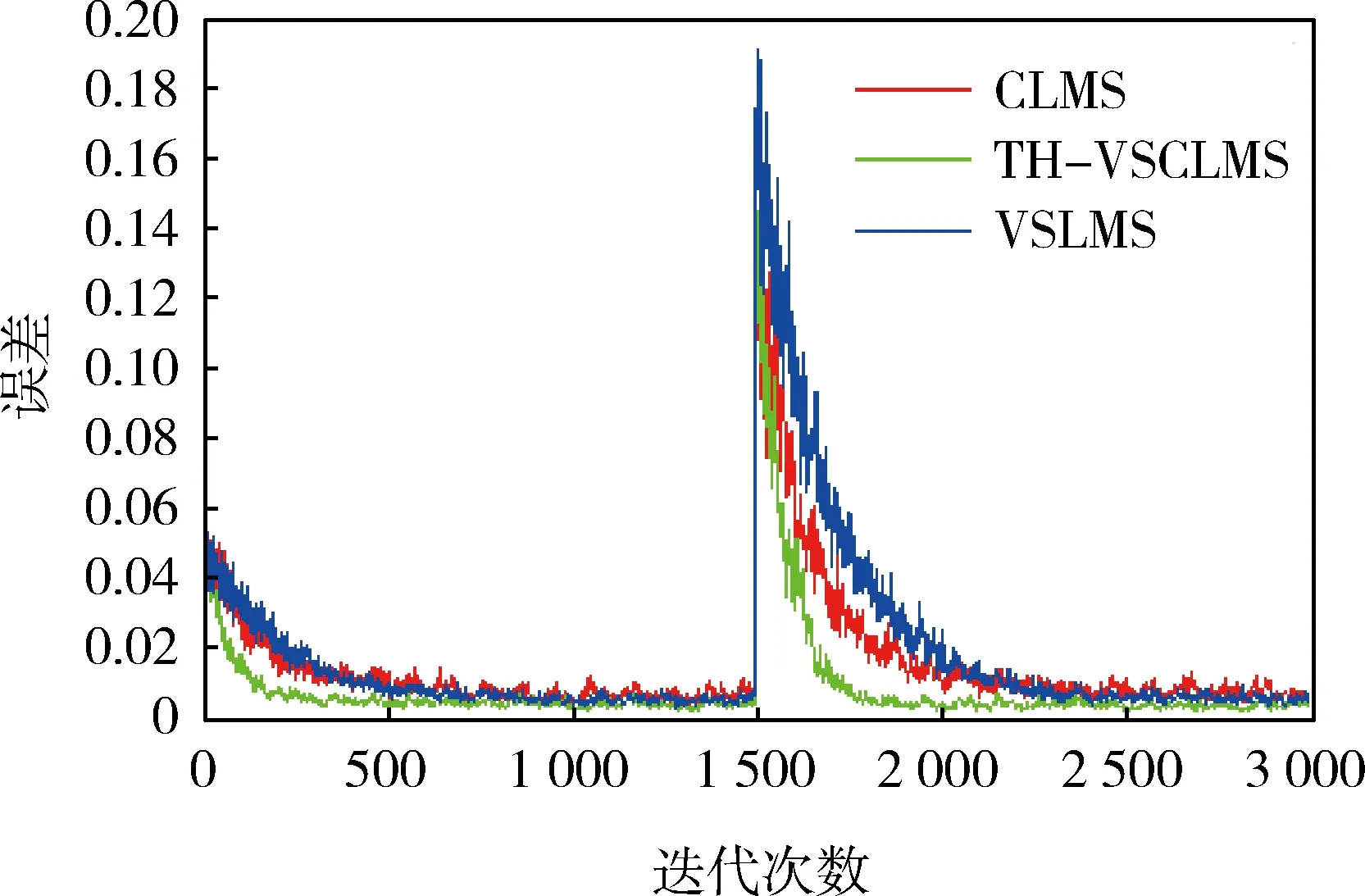
圖3 3種算法的收斂曲線比較

由圖3可見：1)在第1次收斂時，Th-VSCLMS算法迭代到250次時即進入穩態收斂階段，其他2種算法迭代到420次后才進入穩態收斂階段，可見在初始收斂階段，Th-VSCLMS算法以較少的迭代次數進入穩態，計算量較小，穩態誤差最小，表明Th-VSCLMS算法無論在收斂速度還是在穩態誤差方面都表現突出，CLMS算法與VSLMS算法收斂性與穩態性差別不大；2)在第2次收斂時，Th-VSCLMS算法的收斂速度更快，表明Th-VSCLMS算法的抗干擾性能最好，而CLMS算法與VSLMS算法相比，CLMS算法的收斂速度也有明顯改善，表明凸組合結構較單一濾波器優越。

3.2 低信噪比下的性能仿真

比較3種算法在低信噪比下的性能，設高斯白噪聲U的均值為0，方差為1，相應信噪比SNR=0。各算法的收斂曲線對比如圖4所示。

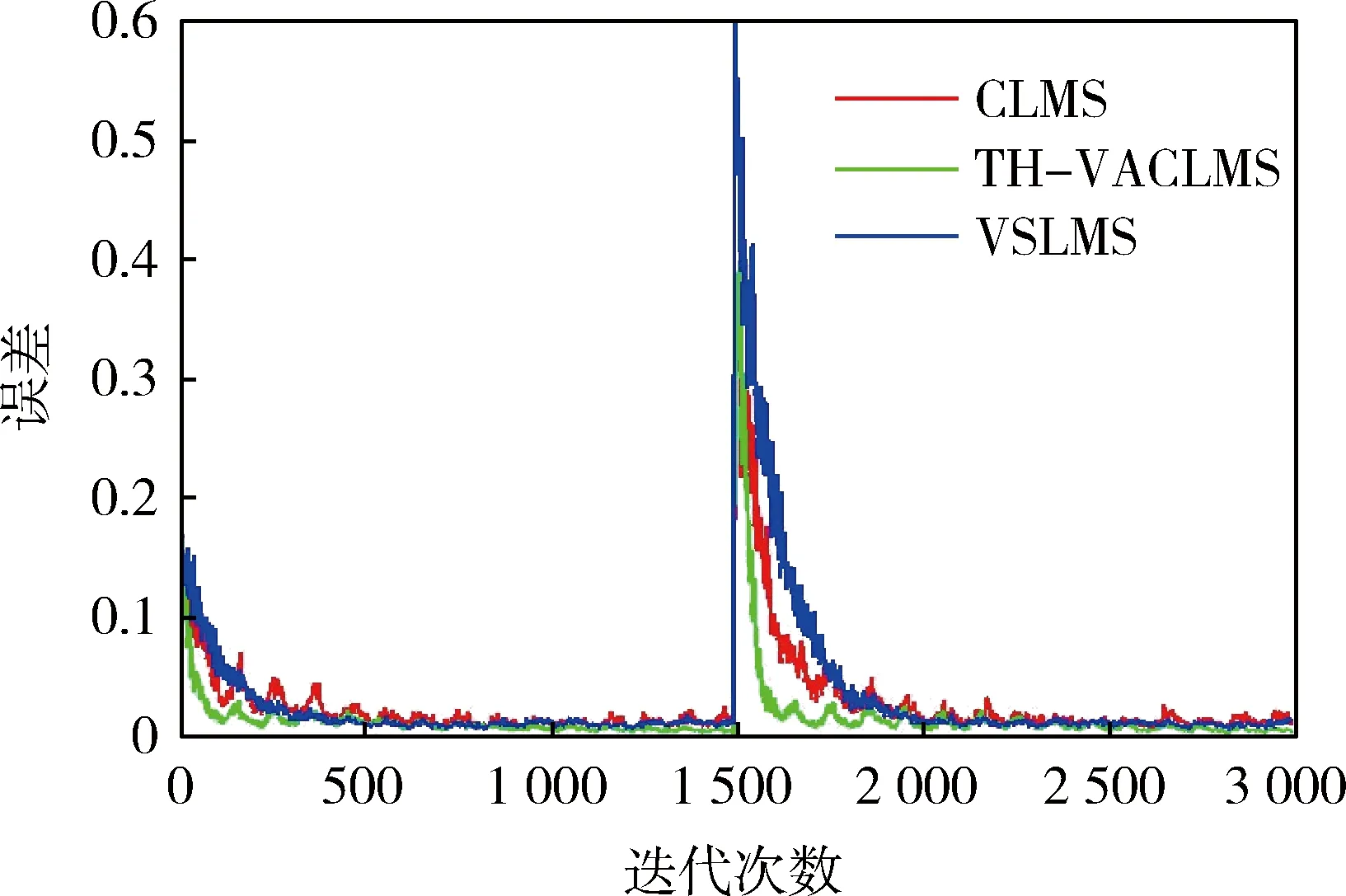
圖4 低信噪比下3種算法的收斂曲線

由圖4可以看出：在低信噪比下，Th-VSCLMS算法仍具有良好的性能。

3.3 結果分析

1) 雖然Th-VSCLMS算法比CLMS算法、VSLMS算法要復雜很多，但其在收斂階段的計算量小，其迭代次數僅為CLMS算法、VSLMS算法的3/5左右，因此較少的迭代次數使三者的計算量相差不大，走出了因其較高復雜度必然帶來更大計算量的誤區。

2) 凸組合結構的抗干擾能力較好。CLMS算法與VSLMS算法在第1次收斂時速度相同，但當權值突變后CLMS算法的收斂速度明顯快于VSLMS算法，表明凸組合結構較優越。

3) 低信噪比下Th-VSCLMS算法在收斂性能和穩態性能方面依然優于其他2種算法。

4 結論

本文基于雙曲正切函數改進了CLMS算法，提出了Th-VSCLMS算法，通過理論與仿真對比分析驗證了該算法性能的優越性。但論文只是從理論與仿真層面驗證了算法，算法的參數選擇雖然基于大量的仿真數據和前人的結論，但不乏會出現誤差，下一步將基于這2方面的問題對算法進行深入研究。

[1] 張立峰,張樹群,雷兆宜，等.基于梯度向量的變步長LMS算法[J].科學技術與工程,2013,13(25):7538-7541.

[2] 呂春英,敖偉,張洪，等.一種新的變步長LMS算法[J].通信技術,2011,44(3):11-14.

[3] 曾召華,劉貴忠,趙建，等.LMS和歸一化LMS算法收斂門限與步長的確定[J].電子與信息學報,2003,25(11):1469-1474.

[4] 高鷹,謝勝利.一種變步長LMS自適應濾波算法及分析[J].電子學報,2001,29(8):1094-1097.

[5] 楊逸，曹祥玉，楊群，等.基于指數函數的歸一化變步長LMS算法[J].計算機工程，2012，38(10):134-136.

[6] Arenas-Garcia J,Figueiras-Vidal A R.Steady-state Performance of Convex Combinations of Adaptive Filters[J].IEEE Signal Pressing,2005,4(4):33-36.

[7] 于霞,劉建昌,李鴻，等.一種變步長凸組合自適應濾波器及其均方性能分析[J].電子學報,2010,38(2):480-484.

[8] 苗俊，芮國勝，張洋，等.變步長凸組合LMS自適應濾波算法及分析[J].應用科學學報,2013,31(5):475-480.

(責任編輯: 王生鳳)

A Convex Combination of Variable Step LMS Algorithm Based on Hyperbolic Tangent Function

CHEN Li-wei, TAN Zhi-liang, CUI Li-dong

(Institute of Electrostatic and Electromagnetic Protection, Ordnance Engineering College, Shijiazhuang 050003,China)

The Convex Combination Least Mean Square(CLMS) algorithm is improved by means of hyperbolic tangent function and the Tanh Variable Step Convex Combination Least Mean Square (Th-VSCLMS) algorithm is proposed accordingly. Theoretically, the improved algorithm is superior to conventional variable step algorithm, and VSLMS, CLMS and Th-VSCLMS algorithm are compared and analyzed at different SNR. Simulation results show that Th-VSCLMS is well improved at convergence, steady, anti-disturbance, filtering effect in the low SNR as well as computation, and the convex combination have better filter structure than a single filter structure.

Convex Combined Least Mean Square algorithm; hyperbolic tangent function; fit factor

1672-1497(2015)05-0094-03

2015-05-13

國防科技重點實驗室基金資助項目(9140C87030413JB34001)

陳立偉(1990-)，男，碩士研究生。

TN713

A

10.3969/j.issn.1672-1497.2015.05.019