湍流條件下防熱瓦縫隙熱環境特性實驗研究

龔紅明, 陳景秋, 李 理, 田潤雨

(1. 重慶大學 航空航天學院, 重慶 400044; 2. 中國空氣動力研究與發展中心, 四川 綿陽 621000)

湍流條件下防熱瓦縫隙熱環境特性實驗研究

龔紅明1,2,*, 陳景秋1, 李 理2, 田潤雨2

(1. 重慶大學 航空航天學院, 重慶 400044; 2. 中國空氣動力研究與發展中心, 四川 綿陽 621000)

在激波風洞中馬赫數6.1、雷諾數6.2×107/m的流場條件下，基于平板模型開展了防熱瓦縫隙熱流測量實驗，研究了湍流平板邊界層情況下T字和十字2種布局縫隙的縫壁熱流分布，以及流向角、縫隙寬度、縫隙深度和縫口臺階高度的變化對縫隙熱環境的影響。結果表明，縫口邊緣特別是T字口迎風壁存在很高的局部熱流，測量峰值達到11.6倍平板值，流向角為30°～60°時2種布局縫隙的熱環境相對較好，縫壁及縫底熱流隨縫隙寬度和縫口臺階增大而升高。

防熱瓦；縫隙；臺階；氣動加熱；風洞實驗

0 引 言

在升力體外形的高超聲速飛行器設計中一般會選用防熱瓦作為主要的氣動熱防護手段。防熱瓦分塊鋪設在飛行器表面，為適應瓦片因受熱產生的膨脹或因結構受力而發生的位移或變形，瓦片間必須預留適度的縫隙。但縫隙引起的局部邊界層分離和再附使當地熱環境變得復雜，如果對局部高熱流預計不當則可能造成當地防熱失效。同時由于狹窄深縫內輻射散熱受阻，較低的熱流也可能導致很高的縫壁溫度。例如美國航天飛機首次飛行后，其機腹和機翼迎風面多處防熱瓦縫隙內的填料和應變隔離墊就因為經受高于預計的加熱，出現了不同程度的碳化現象[1]。

國外對防熱瓦縫隙熱環境的研究開展得較早。在20世紀70年代初，Allan等人通過風洞實驗研究了多種寬深比的凹槽流動(包括寬度1～4mm的狹窄深縫)，測量了槽壁熱流，分析了高熱流區位置和熱流受縫隙寬度的影響[2]。之后，國外學者相繼開展了許多相關的實驗、計算和飛行測量研究[3-7]，為航天飛機等飛行器的防熱瓦縫隙設計提供了重要支持。國內從90年代起也開始了相關研究，在計算方面主要是對簡單布局的縫隙采用基于簡化流動模型的工程方法或數值方法計算縫內熱流和壓力，分析熱流受縫隙尺度和外流參數的影響[8-10]；王世芬、唐貴明等分別在激波風洞上開展了縫隙熱流測量實驗，研究了平板上的矩形縫隙和單個橫縫內的熱流分布[11-12]。但國內的研究報道中一般都取較簡單的布局如單個橫縫或斜縫為對象，忽略了真實情況下交錯縫隙內三維流動的影響，并且很少考慮湍流條件下的情形。

本文在平板模型上模擬了T字和十字2種縫隙布局的防熱瓦陣列，在馬赫數6.1、湍流平板邊界層條件下測量了縫隙壁面典型部位的熱流，分析了縫壁熱流分布的基本規律以及流向角、縫寬、縫深和縫口臺階高度對縫隙熱環境的影響。

1 實驗設備與縫隙模型

實驗在中國空氣動力研究與發展中心超高速所的FD-14激波風洞上進行。該風洞高、低壓段激波管分別長9和18m，內徑150mm；型面噴管出口直徑1.2m，試驗段橫截面2.6m×2.6m；能模擬馬赫數6～16，雷諾數2.1×105～6.7×107/m。

本次實驗來流總溫624K，總壓11.5MPa，馬赫數6.1，雷諾數6.2×107/m，實驗氣體為氮氣。

實驗模型由平板和縫隙組件組裝而成：將瓦片安裝在圓形托盤上形成縫隙布局，再將托盤安裝到平板上。圖1(a)和(b)中分別為T字和十字縫隙布局(長度單位均為mm)。通過旋轉托盤可調整流向角β(縱縫與來流的夾角)，旋轉方向為圖1(a)所示逆時針方向。縫隙尺寸如圖1(b)所示，縫寬w=2、4和6mm，縫深d=5、10和25mm。瓦片表面與平板表面平齊，但可以墊高中央瓦片以與相鄰瓦片間形成縫口臺階，臺階高度h=0、0.5、1和2mm。同一縫隙組件上，各瓦片間縫隙的寬度、深度相同。縫內測點主要位于中央瓦片的上游和兩側壁面，測點的定位和坐標定義如圖1(b)所示。平板迎角α=0°、5°和10°。

使用鉑薄膜傳感器測量熱流。傳感器基體為高硼硅酸玻璃，形狀按測量部位定制。縫壁傳感器(見圖2)的條形薄膜陣列由濺射鍍膜和激光刻蝕等工藝形成，薄膜長3mm、寬0.1mm、厚度小于0.5μm，最小間距0.5mm。傳感器的電阻溫度系數為(2.5‰～3‰)/℃，熱流測量范圍約0.05～200W/cm2。

圖1 實驗模型及縫壁測點分布示意圖

圖2 縫壁熱流傳感器

2 實驗結果與討論

2.1 平板與瓦片表面熱流

在平板前部使用了粗糙帶以促進邊界層轉捩。如圖3所示，實驗時間內測點熱流曲線所反映的邊界層流態變化，以及測量熱流值與湍流計算結果的比較，均說明平板邊界層在縫隙上游已完全轉捩為湍流，且沿平板橫向一致性較好。

對縫壁熱流測量值q采用相應迎角下無縫平板中心線上X=600mm的計算值qfp為參考作無量綱化。由圖4可見，α=0°時各瓦片中心點熱流均與無縫平板值相當，表明縫隙對瓦片中心區熱流干擾較弱；但迎角增大后T字縫對下游流動干擾較強，導致其下游瓦片中心熱流明顯高于平板值。

圖3 平板表面的熱流分布和熱流-時間曲線

圖4 瓦片表面中心點熱流測量結果

2.2 縫隙流動建立情況

FD-14激波風洞定常氣流維持時間較短，而本次實驗中縫隙數量多且布局較復雜，因此需要考察縫內流動建立情況。這可以根據縫壁熱流隨時間的變化過程來分析[13]。實驗表明，中央瓦片縫壁熱流約有至少4ms(18ms≤t≤22ms)的穩定時間，如圖5(a)所示，與平板表面熱流的穩定時間相當，足夠完成熱流測量。并且在中央瓦片縫壁測得的熱流分布規律也與國外常規高超聲速風洞中的實驗結果[14]相符。這表明中央瓦片上游橫縫和側縫內的流動基本達到了穩定狀態。但下游縫隙內流動建立需要更長的時間，以致局部區域的流動未能達到穩定狀態，如圖5(b)所示。因此本次實驗中主要考察中央瓦片上游橫縫及側縫縫壁的熱流。

2.3 基本狀態下兩種布局縫隙的熱環境

基本狀態指w=4mm，d=25mm，h=0mm，β=0°，α=0°。

2.3.1 T字布局縫隙的熱流分布

T字布局縫隙的實驗結果表明(見圖6)，T字口迎風壁、橫縫縫口及瓦片拐角處的縱縫側壁是縫隙內的高熱流區，其峰值熱流均高于平板值，而縫內熱流分布均沿深度方向降低。T字口迎風壁(測位2)由于受到上游縱縫內流動的沖擊，氣動加熱最為嚴重，測量峰值約為11.6倍平板值，且縫口以下約60%深度內的熱流均在平板值的2倍以上。文獻[15]在相近的條件下測得T字口峰值熱流約9.5倍平板值，考慮到縫隙尺寸和測點定位略有差異，可以認為2個實驗的結果是相符的。橫縫迎風壁(測位1、3)縫口邊緣的測量熱流為1～2倍平板值，同時由于上游縱縫的存在造成橫縫內橫向流動較強，其縫壁大面積熱流也較高,在平板值的0.5倍以上。在縱縫側壁面除瓦片拐角處(測位4)與橫縫相當外，縫壁熱流相對較低。

(a) 達到穩定狀態的測點熱流

(b) 未達到穩定狀態的測點熱流

圖6 T字布局中央瓦片縫壁熱流分布

2.3.2 十字布局縫隙的熱流分布

十字布局縫隙內的最高熱流出現在橫縫縫口邊緣，同時縱縫縫壁大面積區域熱流也較高，如圖7所示。橫縫縫口熱流接近2倍平板值但縫內熱流沿深度方向很快降低。縱縫縫口熱流約與平板值相當，同時在長縱縫情況下，縫內入流量大且流動較強，因此縫內熱流也相對較高，縫口以下大面積區域的熱流在0.5倍平板值以上，其中在十字口側壁(測位3)D/d≈0.2位置上出現了約1.5倍平板值的第二處高熱流。因此縱縫內雖然局部高熱流并不突出，但按面積而計的總熱載卻相對較高。

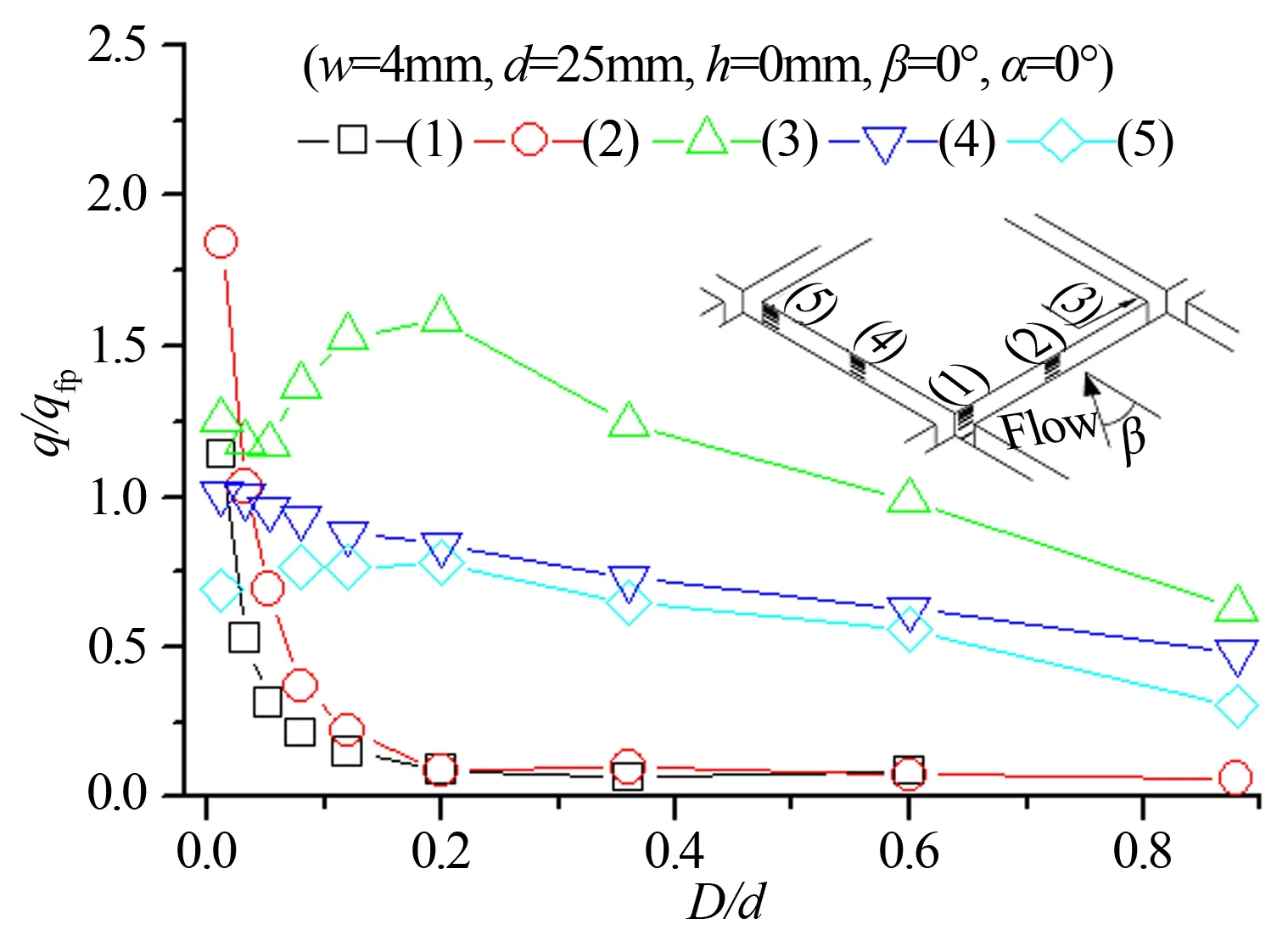
圖7 十字布局中央瓦片縫壁熱流分布

2.4 流向角對縫壁熱流分布的影響

T字布局下，當流向角β增大后，T字口處迎風角度減小，同時上游縱縫入流量減小且縫內流動的沖擊作用減弱，因而T字口迎風壁熱流顯著降低，如圖8所示。β增大時橫縫逐漸向縱縫轉變，縫壁迎風效應減弱但縫內入流量增大，因此縫壁(如測位3)熱流出現先降低后升高的變化；同時，縱縫逐漸向橫縫轉變，因此其縫口熱流升高而縫內熱流降低。若兼顧局部高熱流和縫壁總熱載，可以認為當β≈30°～60°時縫內熱環境較好。

圖8 流向角對T字布局縫壁熱流的影響

十字布局下，在十字口處(測位1)，β增大過程中上游瓦片的遮擋效應減弱使得當地熱流升高，但此后縫壁迎風角的繼續減小又使得當地熱流轉而降低，如圖9所示。在縱縫側壁，β增大時縱縫逐漸向橫縫轉變，縫壁熱流分布也漸與橫縫類似，出現縫口附近熱流升高而縫內大面積熱流降低的變化。此外在橫縫迎風壁上距十字口較遠處(測位2)，熱流對45°以內的β的變化并不敏感。若兼顧局部高熱流和縫壁總熱載，可以認為當β≈45°時縫內熱環境相對較好。

圖9 流向角對十字布局縫壁熱流的影響

2.5 兩種布局縫隙熱環境的比較

β=0°時，由前文可知縫內高熱流主要位于縫隙交叉口和橫縫縫口區域。對縫隙交叉口而言，T字口迎風壁受氣動加熱要遠比十字口嚴重。雖然橫縫縫口邊緣的高熱流都主要是受平板邊界層再附沖擊所致，并且2種布局下這種影響效應基本相當，但T字布局的橫縫內入流流量較大且橫向流動較強，因此T字布局的橫縫縫內大面積區熱流顯著高于十字布局，如圖10(a)所示。同時，β=0°時十字布局的長縱縫側壁熱流顯著高于T字布局下相對較短的縱縫，這表明在設計防熱瓦布局或瓦片尺寸時必須考慮縱縫長度對縫隙熱環境的影響。

β=45°時，除T字布局下縫口邊緣熱流略高以外，整體而言2種布局相似部位的熱流值及其分布基本一致，如圖10(b)所示。若結合到鋪設瓦片的實際情況，可優先選取類似于β≈45°的T字布局這種交錯排列瓦片的方式。

2.6 縫隙參數對縫內熱環境的影響

在T字布局縫隙的基本狀態下分別進行變縫寬、縫深和縫口臺階高度的熱流測量。實驗結果表明，縫寬w=2～6mm范圍內縫壁熱流分布規律基本不變，但縫寬增大后縫內入流增加，縫內流動增強，使縫壁熱流升高，如圖11所示(β=0°時熱流分布變化規律與此相同)。

縫深變化對縫壁熱流的影響因縫壁位置和縫隙走向而異。如圖12所示，在T字口處，當縫深自25mm變淺后熱流有所降低，但d≤10mm范圍內熱流隨縫深的變化并不明顯。縱縫側壁熱流整體隨縫深變淺而升高，橫縫壁面熱流整體上受縫深變化影響較弱。

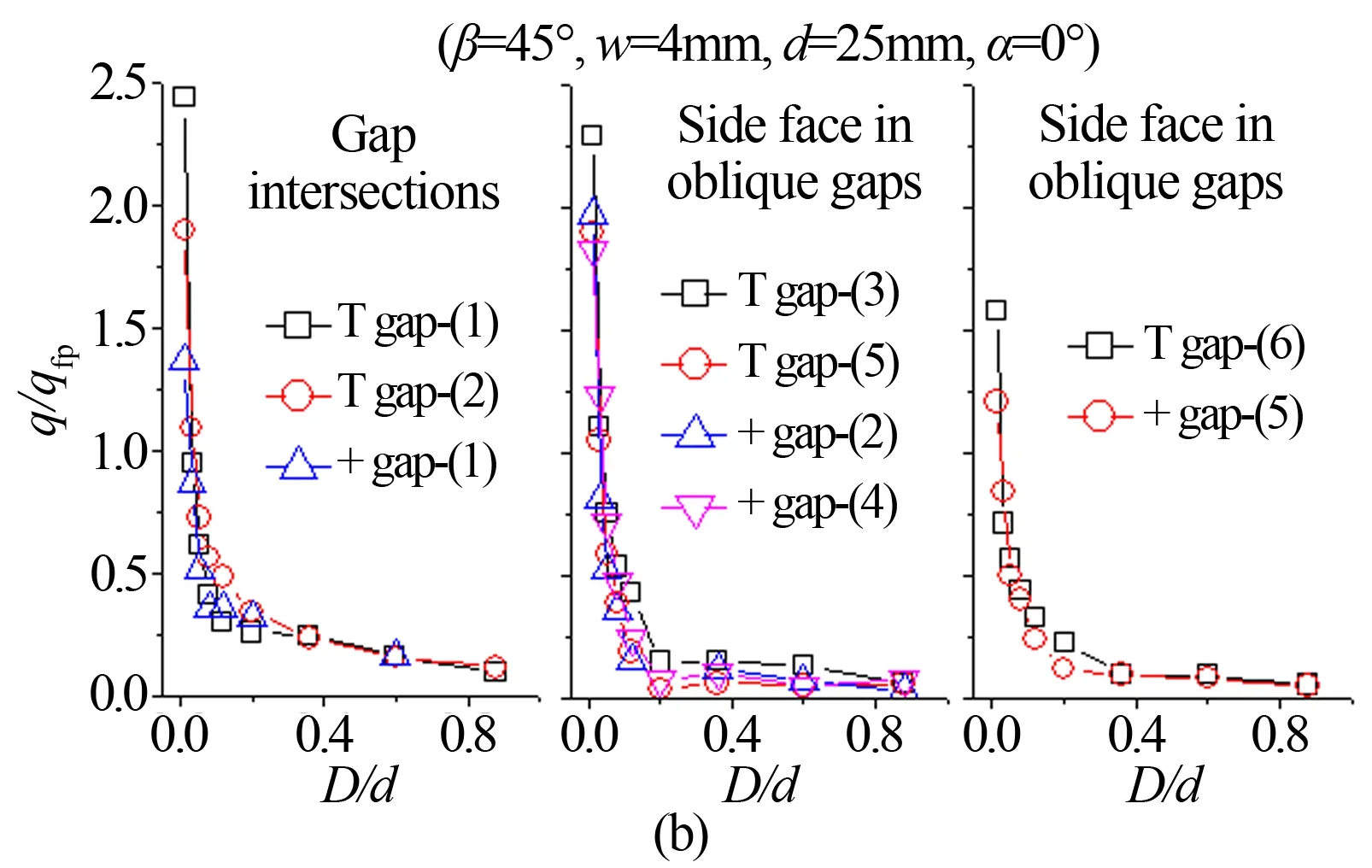
圖10 2種布局縫隙熱流分布的比較

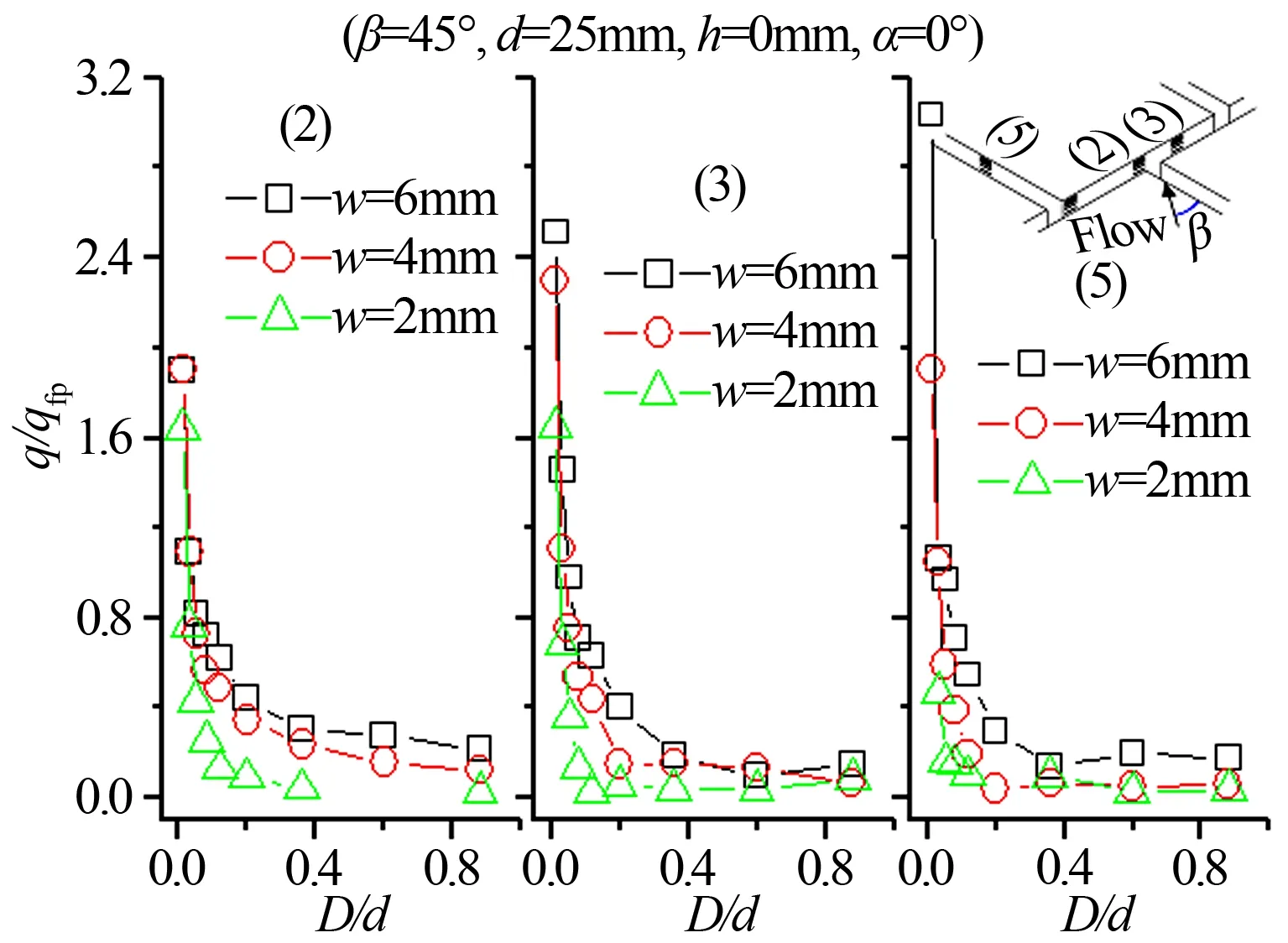
圖11 縫隙寬度對縫壁熱流的影響

縫深變化對縫壁熱流的影響因縫壁位置和縫隙走向而異。如圖12所示，在T字口處，當縫深自25mm變淺后熱流有所降低，但d≤10mm范圍內熱流隨縫深的變化并不明顯。縱縫側壁熱流整體隨縫深變淺而升高，橫縫壁面熱流整體上受縫深變化影響較弱。

縫口存在臺階時縫壁各處熱流變化如圖13所示。由于影響T字口迎風壁熱流的主要因素是上游縱縫流動的沖擊，因此臺階的出現并未引起當地熱流升高。但橫縫和縱縫縫壁熱流隨臺階高度增大而升高，其中橫縫縫口區受縫外邊界層再附作用顯著強于無臺階的情況，因此其縫口熱流測量峰值由無臺階時的1～2倍平板值上升到9倍左右。

圖12 縫隙深度對縫壁熱流的影響

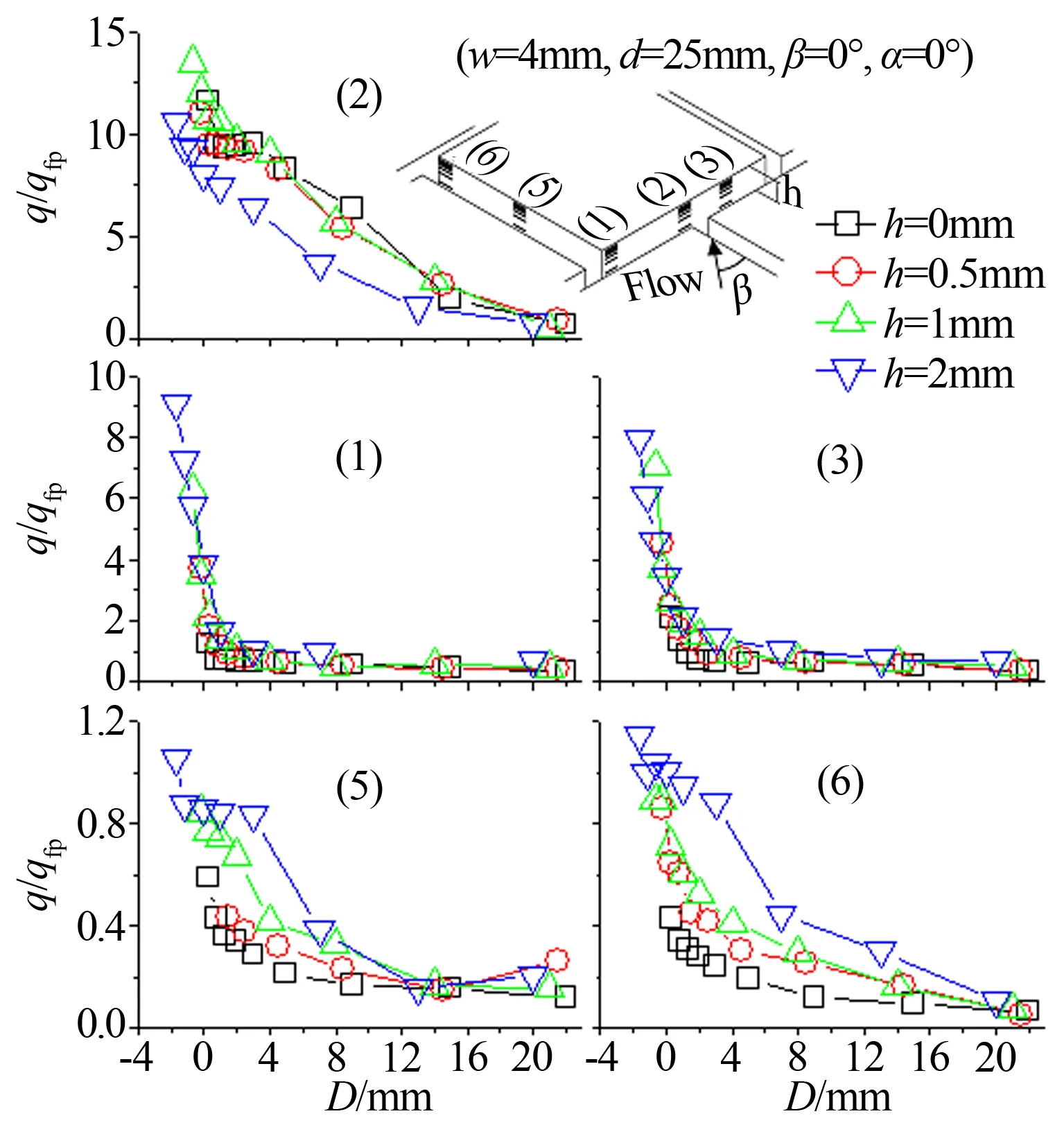
圖13 縫口臺階高度對縫壁熱流的影響

實驗結果表明，縫隙底部熱流隨縫隙深度變淺而升高，受縫隙寬度和臺階變化的影響較小(見圖14)。然而T字口處當縫隙變寬時縫底熱流升高，例如在w=6mm時出現了約1.8倍平板值的高熱流，但該處熱流在β增大后顯著降低。

圖14 縫隙尺寸變化對縫底熱流的影響

2.7 迎角對縫隙熱環境的影響

實驗結果表明增大迎角會使縫內絕對熱流顯著升高，但對無量綱熱流q/qfp影響較小。如圖15所示，在迎角從0°增大到10°過程中，橫縫及斜縫迎風壁熱流q/qfp基本保持一致，這是因為橫縫、斜縫內流動結構相對簡單，迎角變化時能夠保持較好的相似性。但縱縫側壁熱流q/qfp表現出從升高到趨于穩定的變化，即在5°、10°迎角下熱流結果一致，同時相比0°迎角有所升高。這表明縱縫流動能夠在一定迎角范圍內保持相似特性，但同時由于縫內流動十分復雜，例如后向臺階引起的流動分離與再附，以及中央瓦片拐角引起的流動分離和縫隙側壁邊界層增長等，因此縫壁熱流q/qfp也較易受到迎角(或入流馬赫數等)變化的影響。

圖15 迎角變化對T字布局縫壁熱流的影響

3 結 論

根據本次實驗可得以下主要結論：

(1) 各布局下縫隙熱流分布存在以下基本規律：縫隙交叉口、橫縫縫口及瓦片拐角側壁縫口是縫壁高熱流區，其縫沿熱流普遍高于平板值；縫壁熱流沿深度方向降低且在橫縫縫口附近分布梯度較大，在縱縫側壁分布梯度較小；平板迎角的小幅增加使縫內絕對熱流升高，但相對平板值的比熱流變化較小；

(2)β=0°條件下T字口迎風壁受熱嚴重，十字口壁面熱流相對較低且局部峰值與平板值相當。就大面積區而言T字布局的橫縫迎風壁和十字布局的縱縫側壁是縫壁的較高熱流區；

(3) 流向角變化對縫隙熱環境影響顯著，β≈45°時2種布局的縫隙熱環境較優，特別是T字口的高熱流顯著降低；

(4) 縫內熱流主要隨縫寬增大和縫口臺階高度增加而升高，縫深變化對縫壁熱流的影響較復雜，因具體位置而異。

[1] Petly D H, Smith D M, Edwards C L W, et al. Analysis of gap heating due to stepped tiles in the shuttle thermal protection system[R]. NASA TP-2209, 1983.

[2] Wieting Allan R. Experimental investigation of heat transfer distribution in deep cavities in hypersonic seperated flow[R]. NASA ITN-D-5908, 1970.

[3] Weinstein Irving, Avery Don E, Chapman andrew J. Aerodynamic heating to the gaps and surfaces of simulated reusable surface insulation tile arrays in turbulent flow at Mach 6.6[R]. NASA TM-X-3225, 1975.

[4] David Allen Throckmorton. An experimental investigation of heat transfer to reusable surface insulation tile array gaps in a turbulent boundary layer with pressure gradient[R]. NASA CR-141310, 1975.

[5] Foster T F, Lockman W K, Grifall W J. Thermal protection system gap heating rates of the rockwell international flat plate heat transfer model(Oh2a-Oh2b)[R]. NASA CR-134077, DMS-DR-2035, 1973.

[6] Bertin J J, Goodrich W D. Aerodynamic heating for gaps in laminar and transitional boundary layers[R]. AIAA 1980-0287.

[7] Pitts W C, Murbach M S. Flight measurements of tile gap heating on the space shuttle[R]. AIAA 1982-0840.

[8] 童秉綱. 航天飛機防熱瓦縫隙氣動加熱的討論[J]. 氣動實驗與測量控制, 1990, 4(4): 1-7.

Tong Binggang. A qualitative study of tile gap heating on space shuttle[J]. Aerodynamic Experiment and Measurement & Controls, 1990, 4(4): 1-7.

[9] 唐功躍, 吳國庭, 姜貴慶. 縫隙流動分析及其熱環境的工程計算[J]. 中國空間科學技術, 1996, 16(6): 1-7.

Tang Gongyue, Wu Guoting, Jiang Guiqing. Flow analysis and numerical computation of thermal environment in gaps[J]. Chinese Space Science and Technology, 1996, 16(6):1-7.

[10] 秦強, 馬建軍. 陶瓷防熱瓦間縫隙氣動加熱規律研究[J]. 裝備環境工程, 2013, 10(5): 42-46, 51.

Qin Qiang, Ma Jianjun. Aerodynamic heating in gaps among ceramic insulating tiles array[J]. Equipment Enviromental Engineering, 2013, 10(5): 42-46,51.

[11] 唐貴明. 狹窄縫隙內的熱流分布實驗研究[J]. 流體力學實驗與測量, 2000, 14(4): 1-6.

Tang Guiming. An experimental investigation of heat transfer distributions in a deep gap[J]. Experiments and Measurements in Fluid Mechanics, 2000, 4(4): 1-6.

[12] 王世芬, 黃晶, 劉鵬. 天線窗縫隙流傳熱的實驗研究[J].宇航學報, 1995, 16(1): 53-59.

Wang Shifen, Huang Jing, Liu peng. Experimental investigation of heat transfer distributions inside the gap of a antenna window[J]. Journal of Astronautics, 1995, 16(1):53-59.

[13] 唐貴明. 平板-控制翼縫隙熱流分布的激波風洞實驗[J]. 空氣動力學學報, 1985, 6(2):88-91.

Tang Guiming. Experimental investigation of heat transfer distribution inside the gap of a flat plate-flap combination in a shock tunnel[J]. Acta Aerodynamica Sinica, 1985, 6(2):88-91.

[14] Averry Don E. Experimental aerodynamic heating to simulated space shuttle tiles in laminar and turbulent boundary layers with variable flow angles at a nominal Mach number of 7[R]. NASA TP-2307, 1985.

[15] Charbonnier J, Boerrigter H. Contribution to the study of gap induced boundary layer transition in hypersonic flow[R]. AIAA 1993-5111.

(編輯：李金勇)

Experimental investigationon the aerodynamic heating to tile-to-tile gaps in tubulent bouandry layer

Gong Hongming1,2, Chen Jingqiu1, Li Li2, Tian Runyu2

(1. College of Aerospace Engineering, Chongqing University, Chongqing 400044, China; 2. China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China)

The characteristics of aerodynamic heating on tile-to-tile gaps in the flow of Mach number 6.1 with Reynolds number of 6.2×107/m was investigated in shock tunnel. Thermal insulating tiles and tile-to-tile gaps, arranged in T style and + style, were simulated on a flat plate model. Turbulent boundary layer was obtained upstream of the tile gaps by using a grit strip near the leading edge of the flat plate. Heat transfer was measured at the foward faces, side faces and the bottom surface of these gaps, and also at the tiles’ surface. The effect of external flow angularity, gap width, gap depth and misalignment between tiles on the heating distribution in gaps was also examined. Experimental data reveal that the peak heating is most likely to appear on the gap top edges, especially on the forward face at the T-crossing, where a localized peak heating with amplitude approximately 11.6 times larger than that of the flat plate case was measured. It is also indicated that both the localized peak heating and the overall heating are reduced when the flow angle is adjusted to be 30°～60°, and are raised with the increasing gap width and tile-to-tile step height.

thermal insulating tiles;gaps;steps;aerodynamic heating;wind tunnel tests

1672-9897(2015)02-0013-07

10.11729/syltlx20140093

2014-08-13;

2014-11-19

GongHM,ChenJQ,LiL,etal.Experimentalinvestigationontheaerodynamicheatingtotile-to-tilegapsintubulentbouandrylayer.JournalofExperimentsinFluidMechanics, 2015, 29(2): 13-18,25. 龔紅明, 陳景秋, 李 理, 等. 湍流條件下防熱瓦縫隙熱環境特性實驗研究. 實驗流體力學, 2015, 29(2): 13-18,25.

V211.7

A

龔紅明(1981-)，男，四川三臺人，高級工程師。研究方向：激波風洞氣動熱及相關試驗技術。通信地址：四川省綿陽市中國空氣動力研究與發展中心(621000)。E-mail：gh_ming@163.com

*通信作者 E-mail: gh_ming@163.com