改進多重信號分類算法的寬帶頻譜快速感知方法*

孫偉朝，王豐華，黃知濤，王翔(國防科技大學電子科學與工程學院，湖南長沙410073)

改進多重信號分類算法的寬帶頻譜快速感知方法*

孫偉朝，王豐華，黃知濤，王翔
(國防科技大學電子科學與工程學院，湖南長沙410073)

針對寬帶頻譜感知中采樣率大、感知時間長的問題，在調(diào)制寬帶轉(zhuǎn)換器采樣的基礎(chǔ)上提出了一種改進多重信號分類算法的寬帶頻譜快速感知方法。調(diào)制寬帶轉(zhuǎn)換器對寬帶頻譜進行欠奈奎斯特采樣，以最小描述長度準則估計信號個數(shù)，用改進多重信號分類譜估計信號位置。算法引入調(diào)整因子，使得多重信號分類譜中信號位置更為明顯，降低了噪聲的干擾。整個感知過程無須重構(gòu)原始波形，無須計算頻譜，大大降低了計算量，而且感知算法計算復雜度低，提高了感知效率。仿真結(jié)果表明，在低信噪比的情況下，該算法仍具有很好的檢測性能。

寬帶頻譜快速感知；欠奈奎斯特采樣；調(diào)制寬帶轉(zhuǎn)換器；多重信號分類算法

頻譜感知廣泛應用于認知無線電［1-2］、無線電監(jiān)測與頻譜管理等領(lǐng)域。隨著現(xiàn)代通信技術(shù)的發(fā)展，寬帶信號逐步成為一種常見的信號形式。對寬帶頻譜進行感知，過高的采樣率和過大的數(shù)據(jù)量，對現(xiàn)有的模數(shù)轉(zhuǎn)換器(Analog to Digital Converter，ADC)、處理器和存儲設(shè)備等提出了巨大的挑戰(zhàn)。

近年來，Mishali等提出的調(diào)制寬帶轉(zhuǎn)換器(Modulated Wideband Converter，MWC)系統(tǒng)［3］，以寬帶頻譜的稀疏性和壓縮感知(Compressed Sensing，CS)理論［4］為基礎(chǔ)，用遠低于奈奎斯特采樣速率的速率進行采樣，可無損重構(gòu)信號。該系統(tǒng)易于實現(xiàn)，硬件要求低，并能達到Landau最小采樣速率［5］，因此，是一種有效的解決寬帶頻譜采樣率過大問題的方案。

文獻［6］利用欠奈奎斯特采樣值重構(gòu)平穩(wěn)信號的功率譜，進行寬帶頻譜感知；文獻［7］建立了一種空頻2維壓縮感知模型，提出相應的重構(gòu)算法，通過尋找空間小波基的方法檢測信號；文獻［8-9］利用不同的重構(gòu)算法對壓縮后的信號進行重構(gòu)，得到信號的功率譜。這些方法大都是通過重構(gòu)接收信號，計算功率譜進行頻譜感知。重構(gòu)信號算法復雜度較高、運算量較大，用于頻譜感知會引起較大的感知延遲。例如，認知無線電中出現(xiàn)感知延遲，甚至有可能給主用戶造成干擾。

文獻［10］利用多重集采樣提出了一種寬帶頻譜感知方法，直接在時域利用MUSIC算法實現(xiàn)頻譜感知。文獻［11］也利用多重集采樣，基于多重信號分類(Multiple Signal Classification，MUSIC)算法提出了一種動態(tài)門限搜索匹配的信號個數(shù)估計方法。但基于多重集采樣的方法，要求時間延遲部分精確到其奈奎斯特采樣周期量級，對于寬帶頻譜采樣來說，保持各支路之間的精確時延是很困難的。

針對上述存在的問題，孫偉朝等在易于實現(xiàn)的MWC進行欠奈奎斯特采樣的基礎(chǔ)上提出了基于改進MUSIC算法的寬帶頻譜快速感知方法。

1 問題描述

稀疏多帶信號是軍事和民用通信領(lǐng)域經(jīng)常遇到的信號類型［13］。假設(shè)接收信號x(t)是一個稀疏多帶信號，帶寬范圍為［-fnyq/2，fnyq/2］，fnyq是其奈奎斯特采樣速率。其頻譜是由q個互不相交的子帶Xi(f)(i=1，…，q)及對稱的負頻段子帶組成，如圖1所示。所有子帶中的最大的帶寬為B，子帶最大個數(shù)N(N≥2q)，且有所有子帶帶寬之和遠小于信號的奈奎斯特頻率。

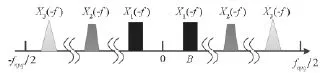
圖1 稀疏多帶信號頻譜Fig.1 Sparsemultiband signal spectrum

整個頻帶等寬度劃分為L個連續(xù)的窄帶信道，每個信道寬度不小于B，信道序號為［1，…，L］。各子帶Xi(f)所處的信道序號組成的集合稱為支撐集［3］。

問題描述如下:預先不知道寬帶頻譜中信號子帶位置的情況下，如何利用MWC得到的壓縮采樣點快速感知子帶所處信道序號，即快速估計出支撐集。

2 MWC欠奈奎斯特采樣

MWC采樣結(jié)構(gòu)如圖2所示，共有m個通道，每個通道都包括一個混頻器、一個低通濾波器和一個ADC。接收到的信號x(t)同時輸入到m個通道，乘上一個周期Tp=1/fp的偽隨機周期序列波形pi(t)，fp為周期序列波形的頻率，且每路的偽隨機序列互不相關(guān)。經(jīng)過截止頻率為1/2Ts的低通濾波器濾波，和采樣率fs=1/Ts的ADC采樣，得到壓縮采樣點yi［n］。

周期序列波形pi(t)按傅里葉級數(shù)展開［3］有

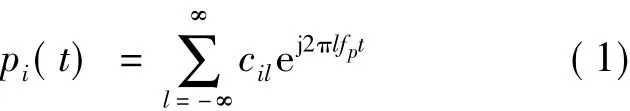
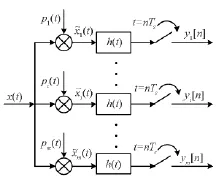
圖2 MWC結(jié)構(gòu)Fig.2 MWC structure

文獻［3］中定理2給出了式(3)有唯一最稀疏解的充分條件。其中，要求m×L的系數(shù)矩陣A中任意2N列線性獨立。

式(3)表示了壓縮采樣序列yi［n］與原始信號x(t)之間的關(guān)系，以及一個求欠定方程組最稀疏解的問題。在感知過程中，文獻［3］提出了連續(xù)到有限(Continue To Finite，CTF)模塊，把式(3)轉(zhuǎn)化為多觀測矢量(Multiple Measurement Vectors，MMV)模型，再利用壓縮感知稀疏重構(gòu)算法求解頻率支撐集，如復雜度低、運行速度快的正交匹配追蹤(Orthogonal Matching Pursuit，OMP)算法［14］等。

3 寬帶頻譜快速感知算法

MUSIC算法是陣列信號處理中經(jīng)典的信號參數(shù)估計方法。孫偉朝等本文借助陣列信號處理模型，對MUSIC算法進行改進，引入調(diào)整因子，比MUSIC算法具有更高的感知正確率。為表述方便，本文算法記為MUSIC_M。

3.1 子空間分析

根據(jù)式(3)，可得到帶噪聲的觀測序列y［n］的頻域表達式

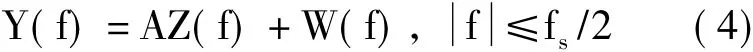
其中W(f)代表高斯噪聲，其分布為N(0，σ2wI)，且與信號不相關(guān)。

觀測矢量的自相關(guān)矩陣

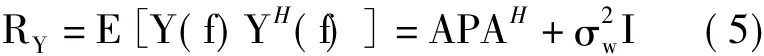
其中，E［·］是求期望，H表示共軛轉(zhuǎn)置，P是信號矢量的自相關(guān)矩陣。對RY進行特征值分解，得到信號子空間Es和噪聲子空間En。

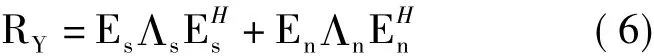
其中，Λs和Λn分別表示由信號和噪聲的特征值構(gòu)成的對角陣，Es和En是對應的特征向量矩陣。假定觀測長度為K，自相關(guān)矩陣RY可通過式(7)估計。

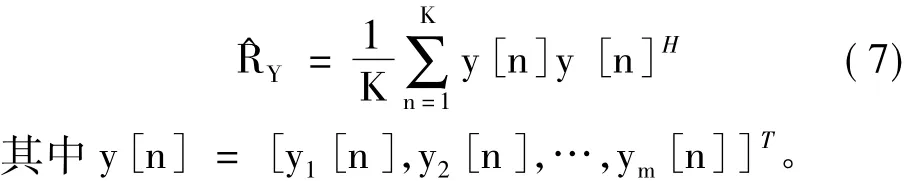
信號個數(shù)估計采用最小描述長度(Minimum Description Length，MDL)準則，MDL準則在決策過程中不需要人工參與，能夠直接利用觀測矢量計算出所含有的信號數(shù)目［12］，即信號個數(shù)的估計值q^。

3.2 改進的MUSIC算法

估計出信號個數(shù)q^之后，m-q^個小特征值即為噪聲的特征值，對應的噪聲特征向量矩陣E^n是其噪聲子空間。MUSIC算法公式［10］為

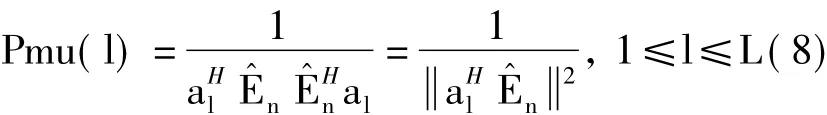
其中，·表示2范數(shù)，l是信道序號，al表示系數(shù)矩陣A的第l列。

由式(1)可得知，系數(shù)矩陣A與窄帶遠場信號的波達方向(Direction of Arrival，DOA)數(shù)學模型中的系數(shù)矩陣存在差異，矩陣各元素的模不恒定。因此，直接計算MUSIC譜易受到“噪聲”干擾。而整個空間(噪聲子空間和信號子空間)的MUSIC譜中包含了所有“噪聲”信息，可以用來

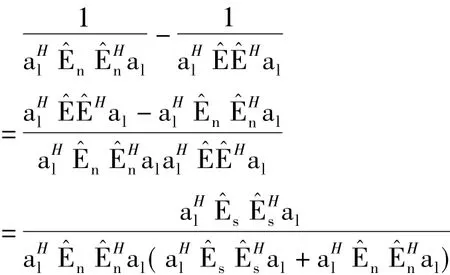
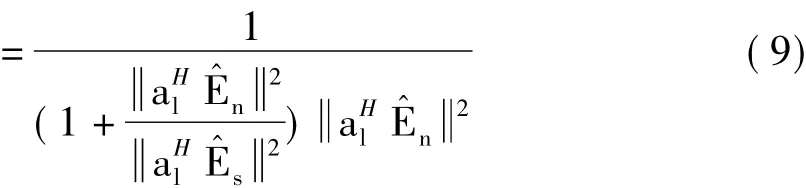
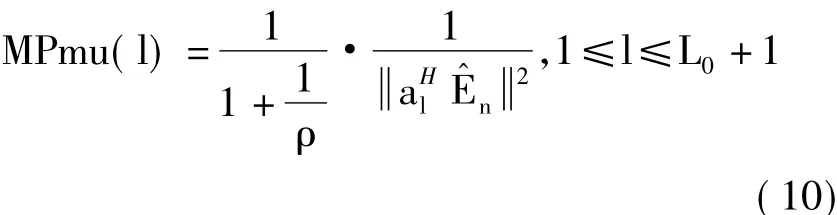
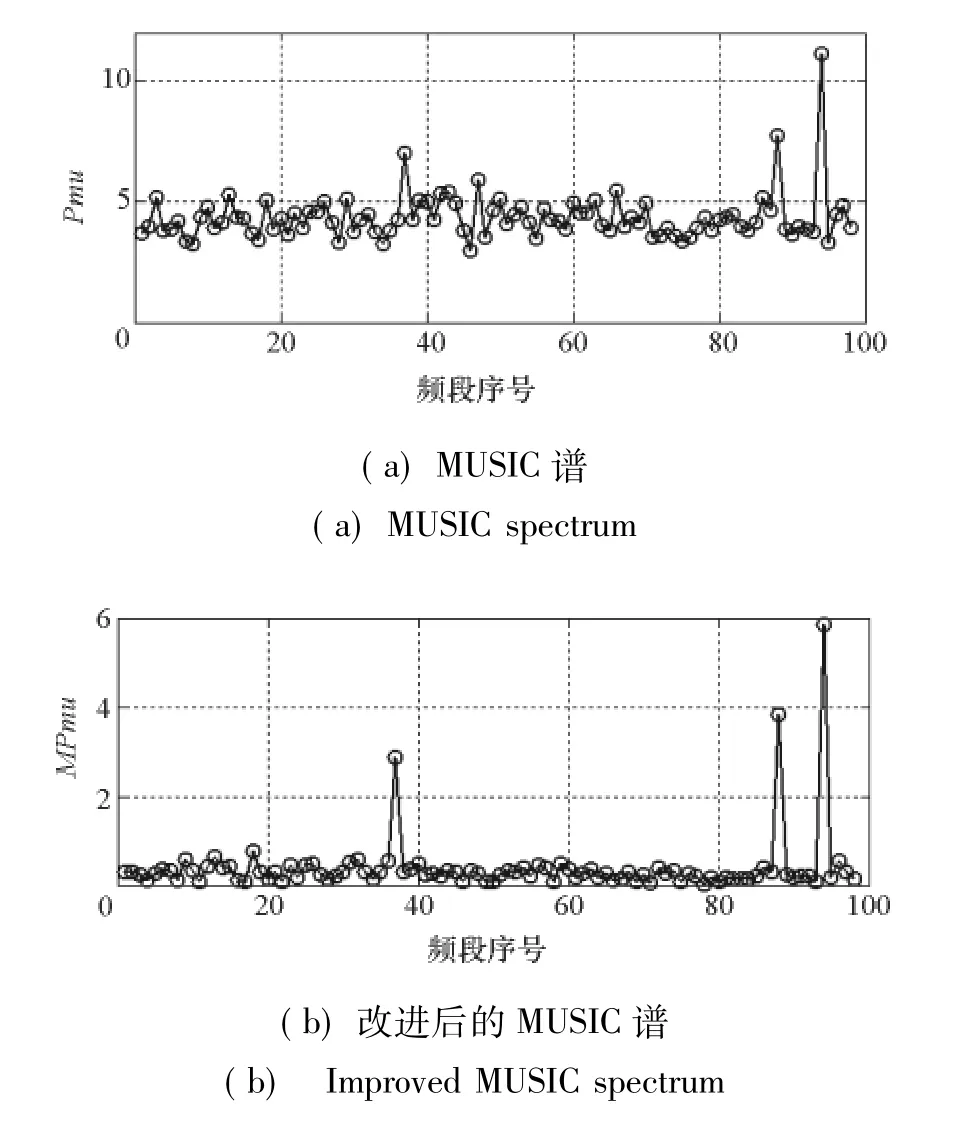
圖3 信號支撐集為{37，88，94}時的MUSIC譜和改進后的MUSIC譜Fig.3 MUSIC spectrum and improved MUSIC spectrum with frequency support{37，88，94}

MUSIC_M算法的主要步驟為:

1)利用MWC對寬帶模擬信號采樣，得到壓縮采樣序列y［n］；

3)進行特征值分解，特征值按從大到小排序，得到特征值d和對應的特征向量矩陣E；

4)利用MDL準則估計信號個數(shù)^q；

5)利用式(10)計算譜MPmu；

3.3 算法復雜度分析

文獻［15］也提出了基于MWC采樣的寬帶頻譜感知方法。利用MDL準則估計信號個數(shù)，應用OMP算法感知頻譜。下面把基于OMP的感知算法與MUSIC_M算法在計算復雜度方面進行分析比較。

3.3.1 基于OMP算法的寬帶頻譜感知復雜度分析

基于OMP算法的寬帶頻譜感知方法與MUSIC_M算法的計算量差異主要體現(xiàn)在OMP算法上。下面在文獻［16］的基礎(chǔ)上分析上述OMP算法的復雜度。

在第t次迭代中，OMP算法中計算選取與殘差相關(guān)性最強的列的集合的復雜度為O(mLK)；然后更新殘差Res(t)=V-(，Moore-Penrose偽逆()?=［(，維數(shù)為m×2t。而2t×2t的復矩陣求逆至少需要O［(2t)3］的計算量，那么上述求殘差過程的計算復雜度為O［m(2t)K+m(2t)2+(2t)3］。因此，OMP算法中第t次迭代的計算復雜度為O［mLK+m(2t)K+m(2t)2+(2t)3］。

3.3.2 MUSIC_M算法復雜度分析

MUSIC_M算法與OMP算法相比，計算量的主要差別在于計算譜MPmu上。

譜MPmu共需計算L0+1=(L+1)/2個值，每個值中的計算復雜度為O(2m2+m)，的復雜度為O［2m(m-q^)+m］。那么，+1點的計算復雜度O［(L+1)(2m2+mmq^)］。可以看出，信號個數(shù)越多，計算量越小；當q^=1時，計算量最大，計算復雜度為O［2(L+1) m2］。根據(jù)文獻［3］要求m≥4q^才能全盲恢復信號，當q^=m/4時那么L0+1點的計算復雜度的乘法次數(shù)最少，約為O［(L+1)(7/4m2+m)］。

3.3.3 算法復雜度比較

基于上述分析，表1給出了兩種方法的計算復雜度比較。

表1 兩種感知算法計算復雜度比較Tab.1 Computational complexity comparison of two sensingmethods

MWC中，L＞m≥4^q，采樣長度K≥m。當^q≥2時，OMP算法的復雜度高于MUSIC_M算法，且隨著信號個數(shù)的增加，其復雜度也會快速增加；而MUSIC_M算法的復雜度會隨著信號個數(shù)的增加而降低。一般寬帶頻譜中的信號個數(shù)都會多于1個，因而，應用MUSIC_M算法比OMP算法能快速感知頻譜。

4 仿真實驗

稀疏多帶信號由式(1)模型產(chǎn)生［10］。

其中:si(t)～N(0，實驗中假設(shè)所有信號功率相同，即=σ2；h(t)為窄帶低通濾波器；q表示信號個數(shù)；w(t)～N(0，)為加性高斯白噪聲，帶內(nèi)信噪比SNR=σ2/。

設(shè)置信號的有效帶寬范圍為［0，500MHz］，即fnyq=1GHz，信號個數(shù)q=3，譜帶數(shù)目N=6，選取通道數(shù)m=30，采樣長度K=101；載頻fi隨機產(chǎn)生，各信號互不交疊，每個信號帶寬都為B= 5MHz，選取信道數(shù)L=195。則每個通道的采樣率fs=fnyq/L=5.13MHz，平均采樣率mfs= 153.9MHz，只有奈奎斯特采樣率的15.4%，大大降低了采樣率，實現(xiàn)了低速采樣。

每個信噪比下進行500次蒙特卡洛仿真實驗，以式(12)～(13)所示的估計值的檢測概率和虛警概率分析算法性能［15］。

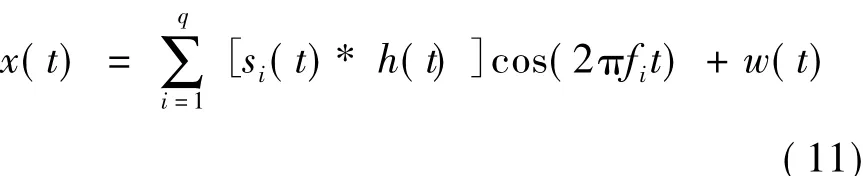
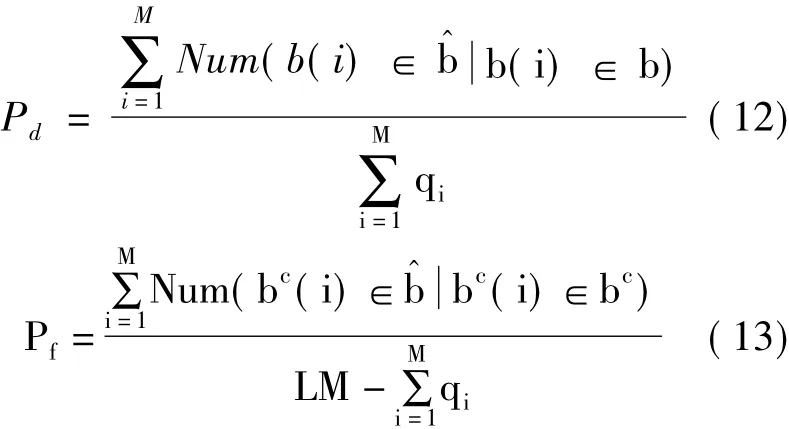
其中:qi表示第i次實驗產(chǎn)生的信號個數(shù)；Num(b(i)b(i)∈b)表示一次實驗中，實際支撐集b與估計支撐集中相同元素的個數(shù)；Num((i)∈i)∈bc)表示一次實驗中，實際支撐集的補集bc與估計支撐集中相同元素的個數(shù)。

圖4和圖5分別給出了在不同信噪比下MUSIC_M，MUSIC和OMP算法的檢測概率曲線和虛警概率曲線。由圖4、圖5可見:同信噪比下，MUSIC_M算法的檢測概率比MUSIC算法的高，并且在15dB時接近于1；其虛警概率比MUSIC算法的低，并且在15dB時接近于0。同信噪比下，MUSIC_M算法的檢測概率和OMP算法的基本一樣，虛警概率也基本一樣。

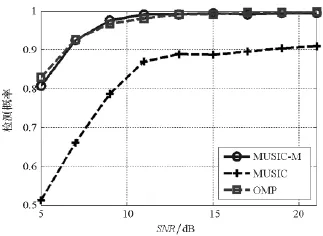
圖4 MUSIC_M，MUSIC，OMP算法檢測概率比較Fig.4 Detection probability comparisons between MUSIC_M，MUSIC and OMP

圖6 給出了信號個數(shù)q從1增加到6時，MUSIC_M算法與OMP算法在所用的平均時間。從圖6中可以看出，在信號個數(shù)多于1時，MUSIC_M算法的處理時間遠低于OMP算法，而且不隨信號個數(shù)的增加而增加。

5 結(jié)論

本文采用MWC采樣來解決寬帶頻譜感知中的采樣率過高和多重集采樣等硬件難以實現(xiàn)等問題；用MDL準則估計信號個數(shù)，并引入調(diào)整因子改進MUSIC譜估計算法，來估計信號的支撐集，從而完成寬帶頻譜感知。與基于OMP的感知算法相比，MUSIC_M算法在不損失感知正確率的基礎(chǔ)上，大大降低了算法復雜度，減少了感知時間，實現(xiàn)了寬帶頻譜快速感知。

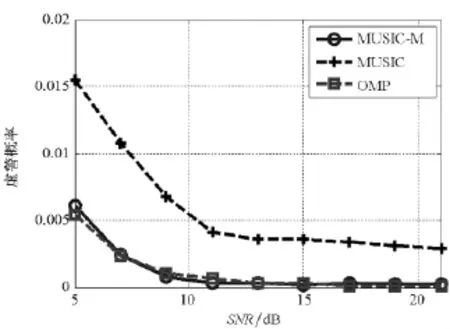
圖5 MUSIC_M，MUSIC，OMP算法虛警概率比較Fig.5 False alarm probability comparisons between MUSIC_M，MUSIC and OMP

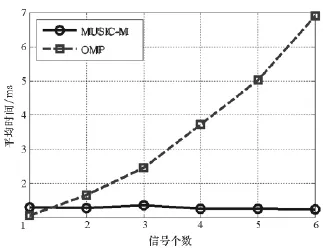
圖6 信號數(shù)不同時MUSIC_M與OMP算法耗時比較Fig.6 Average time comparisons between MUSIC_M and OMP

References)

［1］Bao D，Vito L D，Rapuano S.A histogram-based segmentation method for wideband spectrum sensing in cognitive radios［J］.IEEE Transactions on Instrumentation and Measurement，2013，62(7):1900-1908.

［2］Sharma S K，Chatzinotas S，Ottersten B.Compressive sparsity order estimation for wideband cognitive radio receiver［J］.IEEE Transactions on Signal Processing，2014，62(19):4984-4996.

［3］Mishali M，Eldar Y C.From theory to practice:sub-Nyquist sampling of sparsewideband analog signals［J］.IEEE Journal of Selected Topics in Signal Processing，2010，4(2):375-391.

［4］Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289-1306.

［5］Landau H J.Necessary density conditions for sampling and interpolation of certain entire functions［J］.Acta Mathematica，1967，117(1):37-52.

［6］Cohen D，Eldar Y C.Sub-nyquist sampling for power spectrum sensing in cognitive radios:a unified approach［J］.IEEE Transactions on Signal Processing，2014，62(15): 3897-3910.

［7］王韋剛，楊震，胡海峰.一種寬帶頻譜檢測的空域頻域壓縮感知方法［J］.電子與信息學報，2013，35(2): 255-260.WANGWeigang，YANG Zhen，HU Haifeng.A method of space-frequency compressed sensing on wideband spectrum detection［J］.Journal of Electronics＆Information Technology，2013，35(2):255-260.(in Chinese)

［8］Zhang Z H，Li H S，Yang D P，et al.Space-time Bayesian compressed spectrum sensing for wideband cognitive radio networks［C］//Proceedings of IEEE Symposium on New Frontiers in Dynamic Spectrum，2010:1-11.

［9］Wang Y，Pandharipande A，Leus A.Compressive sampling based MVDR spectrum sensing［C］//Proceedings of 2010 2nd International Workshop on Cognitive Information Processing，2010:333-337.

［10］Rashidi M，Haghighi K，Owrang A，et al.A wideband spectrum sensingmethod for cognitive radio using sub-Nyquist sampling［C］//Proceedings of Digital Signal Processing Workshop and IEEE Signal Processing Education Workshop，2011:30-35.

［11］趙知勁，張鵬，尚俊娜，等.基于MUSIC算法的寬帶頻譜感知［J］.計算機工程，2012，38(13):83-92. ZHAO Zhijin，ZHANG Peng，SHANG Junna，et al.Wideband spectrum sensing based on MUSIC algorithm［J］.Computer Engineering，2012，38(13):83-92.(in Chinese)

［12］Wax M，Kailath T.Detection of signals by information theoretic criteria［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1985，33(2):387-392.

［13］楊鵬，樊昀，黃知濤，等.基于Sub-Nyquist采樣的單通道頻譜感知技術(shù)［J］.國防科技大學學報，2013，35(4): 121-127.YANG Peng，F(xiàn)AN Yun，HUANG Zhitao，et al.Singlechannel spectrum sensing technique based on sub-Nyquist sampling［J］.Journal of National University of Defense Technology，2013，35(4):121-127.(in Chinese)

［14］Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit［J］.IEEE Transactions on Information Theory，2007，53(12):4655-4666.

［15］趙知勁，張鵬，王海泉，等.基于OMP算法的寬帶頻譜感知［J］.信號處理，2012，28(5):723-728.ZHAO Zhijin，ZHANG Peng，WANG Haiquan，et al.Wideband spectrum sensing based on OMP algorithm［J］.Signal Processing，2012，28(5):723-728.(in Chinese)

［16］Sturm B L，Christensen M G.Comparison of orthogonal matching pursuit implementations［C］//Proceedings of 20th European Signal Processing Conference，2012:220-224.

W ideband spectrum fast sensing method based on improved multip le signal classification

SUNWeichao，WANG Fenghua，HUANG Zhitao，WANG Xiang
(College of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，China)

Aiming at the problem of exorbitant sampling rate and sensing time too long in wideband sensing，a wideband spectrum sensing method using improved multiple signal classification(MUSIC)based onmodulated wideband converter(MWC)was proposed.The MWC for sub-Nyquist sampling was used，the number of signals byminimum description length(MDL)criterion was estimated，and the signals’location using improved MUSIC was estimated.In the improved MUSIC，an adjustment factor was given，which enhanced the MUSIC spectrum at the signal’locations and reduced others，and the noise jam was restrained.An amount of calculations was reduced，because it neither needed to recover original wave，nor calculated PSDs in the whole process.The complexity of sensingmethod was small，so that it increased sensing efficiency.The results show a reliable detection even in low signal noise ratio.

wideband spectrum fast sensing；sub-Nyquist sampling；modulated wideband converter；multiple signal classification

TN911.7

A

1001-2486(2015)05-155-06

10.11887/j.cn.201505024

http://journal.nudt.edu.cn

2014-12-09

國家自然科學基金資助項目(61302141)

孫偉朝(1986—)，男，河南夏邑人，博士研究生，E-mail:sweichao1266@163.com；黃知濤(通信作者)，男，教授，博士，博士生導師，E-mail:taldcn@sina.com