高速風洞連續變速壓顫振試驗技術研究

郭洪濤, 閆 昱, 余 立, 呂彬彬, 杜 寧

(1. 中國空氣動力研究與發展中心 空氣動力學國家重點實驗室, 四川 綿陽 621000; 2. 中國空氣動力研究與發展中心 高速空氣動力研究所, 四川 綿陽 622763)

高速風洞連續變速壓顫振試驗技術研究

郭洪濤1,2,*, 閆 昱2, 余 立2, 呂彬彬2, 杜 寧2

(1. 中國空氣動力研究與發展中心 空氣動力學國家重點實驗室, 四川 綿陽 621000; 2. 中國空氣動力研究與發展中心 高速空氣動力研究所, 四川 綿陽 622763)

針對高速暫沖式風洞階梯變速壓顫振試驗用時長、耗氣量大和試驗模型有效使用壽命短等缺點，開展了高速暫沖式風洞連續變速壓顫振試驗技術研究，解決了定Ma數連續變速壓流場控制技術與連續變速壓工況下的顫振試驗數據處理技術等難題。具體技術措施是：在2.4m×2.4m暫沖式跨聲速風洞中設計了基于運動函數的定Ma數線性變總壓控制策略，使Ma數控制精度達到了0.005以內且速壓無超調，實現了流場控制目標；采用Pick-Hold方法構建顫振邊界的亞臨界預測判據，并根據預測判據近似于正態分布的特點，基于數理統計的參數估計法來減小預測判據的散布度，從而提高顫振邊界亞臨界預測的準確性。風洞驗證試驗結果表明，該試驗技術達到了工程實用化水平，不僅能夠取得與階梯變速壓顫振試驗技術一致的結果，還能極大地節省耗氣量，經濟效益顯著。

顫振；氣動彈性；風洞試驗；試驗技術；流場控制

0 引 言

顫振是飛行器氣動力、彈性力和慣性力相互耦合引發的一種自激發散振動，嚴重時可導致飛行器空中解體。顫振邊界決定飛行包線范圍，影響作戰性能，是先進飛行器結構設計必須考慮的關鍵因素。因此，準確預測顫振邊界是飛行器研制中必須解決的重大技術問題。獲取飛行器顫振邊界主要有計算和試驗2種手段。顫振計算主要針對亞聲速與超聲速情況，而對于跨聲速范圍的顫振，由于流動的復雜性，目前的數學模型和硬件設備還無法給出準確可靠的結果。顫振風洞試驗則可以利用風洞再現顫振現象，校核顫振邊界，研究顫振特性，其結果也為顫振飛行試驗提供依據[1-2]。

在高速風洞顫振試驗領域，國內通常的做法是采用定Ma數階梯變速壓的開車方式來獲取顫振邊界。設置速壓階梯的目的是獲取一定長度的振動信號數據，然后采用基于平穩隨機信號的數據處理方法來計算顫振穩定性參數。然而，在確保試驗結果精準度的前提下，相對階梯變速壓顫振試驗方法來說，連續變速壓顫振試驗方法具備3大優勢：(1)試驗時間短，耗氣量小，經濟效益顯著；(2)顫振邊界預測參數曲線更加光滑連續，試驗結果信息量更大；(3)試驗速壓可連續逼近顫振臨界點，避免階梯變速壓工況下的超臨界情況，試驗安全性更高。

隨著風洞流場控制技術與測試設備性能的不斷提升，以及非平穩信號分析理論的提出，國外率先開始發展基于非平穩隨機信號數據處理的連續變速壓顫振試驗方法。1990年，NASA蘭利研究中心的Robert V報道了可用于連續變速壓顫振試驗的亞臨界分析方法[3]，即Pick-Hold方法。該方法從理論上分析了速壓與顫振模型振動能量的關系，并和其它方法作了比較研究。1994年7月，洛克希德馬丁公司在NTS的4ft×4ft亞跨超三聲速風洞中采用連續變速壓顫振試驗方法進行了F-22的垂尾顫振試驗，并獲得了需要的硬顫振點[4]。日本國家宇航實驗室的Yuji Matsuzakai于1998年提出了DTFM(Discrete Time Flutter Margin)方法[5]，該方法基于ARMA模型獲得連續變速壓顫振試驗數據的穩定性參數，與階梯變速壓方法不同的是，穩定性參數隨速壓變化是一條連續線。1999年，該方法成功應用于一個超聲速斜置翼的顫振試驗[6]。但是，通過理論分析與數值仿真，筆者發現ARMA模型對于同時有輸入與輸出數據的系統具有一定的適用性，對于只有輸出響應的連續變速壓顫振試驗數據其應用效果則欠佳，這在NASA的Robert Walker等人的研究中也得到了證實[7]。

本文基于國內外相關研究成果與已有技術基礎，在流場控制方面，設計基于運動函數的定Ma數線性變總壓控制策略，實現2.4m跨聲速風洞的定Ma數連續變速壓流場控制；在數據處理技術方面，提出一種連續變速壓顫振試驗數據的預處理方法，基于Pick-Hold方法構建顫振邊界的亞臨界預測判據，并根據預測判據隨速壓的變化近似于正態分布的特點，利用數理統計理論的參數估計方法減小預測判據的散布度，以提高連續變速壓試驗工況下顫振邊界亞臨界預測的可靠性。

1 試驗設備與方法

1.1 風洞與模型

本研究在中國空氣動力研究與發展中心高速所的2.4m×2.4m風洞(FL-26風洞)半模試驗段中進行。該風洞是一座試驗段橫截面為2.4m×2.4m的引射式、半回流、暫沖型跨聲速風洞。試驗Ma數范圍為0.3～1.4。半模試驗段上、下壁開有與氣流方向成60°、直徑為24mm的斜孔，主要目的是消除跨聲速時的激波反射干擾；左右側壁為實壁，左側有轉窗機構，右側有隨動轉窗壁，可以實現安裝于側壁模型迎角變化。

研究模型為大展弦比超臨界機翼，該模型是滿足氣動外形、剛度分布和質量分布相似的動力學相似模型。為了模擬機身的氣動影響，機翼通過剛性機身與風洞側壁轉窗連接。根據機翼模型結構設計布局，模型采用鋁合金單梁加復合材料應力蒙皮形式，內部填充聚胺脂泡沫。各個梁、肋的截面尺寸和蒙皮厚度均由模態優化計算后的結果確定，梁與肋之間靠角片連接，連接后縫隙用環氧樹脂膠接，蒙皮與梁、肋之間主要靠環氧樹脂膠接。結構設計完成后的模型梁、肋示意如圖1所示。

圖1 模型內部結構示意圖

經過優化，模型設計結果的前3階模態頻率與真實飛機誤差小于1.2%，模態置信判據(MAC)矩陣對角線值大于0.96。經過地面模態試驗檢測，實際加工得到的模型前3階模態頻率誤差小于6%。具體結果如表1所示。

表1 模型的模態設計及檢測結果

1.2 測試儀器

試驗時，采用粘貼于主梁上的電阻絲應變計(中國航空集團制造，EF1000-4AA-AM(11)-X)來測量機翼的彎曲與扭轉變形；采用安裝于翼尖的加速度傳感器(美國Entran公司制造，EGAX-100-C20001)來測量機翼的振動加速度。數據采集系統采用美國國家儀器公司(National Instruments，以下簡稱NI公司)的并行數據采集模塊PXI-4472，最高采樣率為10k/s；信號調理系統采用NI公司的SCXI-1520多功能信號調理模塊。理論上該系統的測量絕對誤差為0.1mV，考慮到噪聲干擾，實際的測量誤差要大于0.1mV，一般為0.2～0.5mV。

1.3 試驗方法

連續變速壓顫振試驗技術是在保持風洞流場Ma數不變的前提下連續增加試驗速壓，直至接近或達到該Ma數下模型的顫振臨界點。在此過程中，流場控制系統保持流場受控，數據采集系統以一定的采樣率采集應變計、加速度傳感器和總靜壓傳感器的電壓信號。為了避免模型與風洞試驗設備因模型發生顫振而損壞，試驗中采取了計算機程控關車與人工監視關車2種方式來實現風洞“緊急關車”。

吹風結束后，可視具體情況來確定顫振臨界速壓。若吹風速壓僅達到顫振亞臨界范圍，則需要通過外插獲取該Ma數下的顫振臨界速壓；若試驗時直接吹到了顫振臨界點，則無需再進行外插計算。

2 關鍵技術及解決措施

高速風洞顫振試驗的關鍵技術主要包含4個方面：(1)顫振模型研制；(2)定Ma數變速壓流場控制；(3)顫振試驗數據處理；(4)顫振模型與試驗設備防護。對于連續變速壓顫振試驗來說，上述的(1)、(4)點與階梯變速壓顫振試驗是一致的，詳情可參考文獻[8]，本文主要針對第(2)、(3)點進行分析和說明。

2.1 流場控制

FL-26風洞用于流場建立的控制系統包括主引射器調壓閥控制系統、主排氣閥穩定段總壓控制系統、柵指Ma數控制系統、駐室流量閥Ma數控制系統和駐室引射器調壓閥控制系統。受風洞閉合回路的影響，風洞穩定段總壓和試驗段Ma數可表示為：

(1)

式中：p0為穩定段總壓，ps為穩定段靜壓，Ma為試驗段馬赫數，py為主引射器引射壓力，Sfig為柵指位移，SZL為駐室流量閥位移；pfy為輔引射器引射壓力，SME為主排位移。從式(1)可以看出，2.4m風洞是一個多輸入兩輸出的多變量控制系統[9]。

根據FL-26風洞的特點，我們設計了基于運動函數的定Ma數線性變總壓控制策略。通過對Ma數的閉環調節，確保了Ma數的控制精度。具體做法是：起動風洞，建立流場到起始總壓p1，然后以一定的總壓變化率V來給定總壓的值，待到達目標總壓p2后，保持總壓的調節狀態，如圖2所示，其運動函數如式(2)所示。在總壓的線性變化過程中，由于設定的總壓與反饋總壓之間的偏差通常比較小，通過整定PID參數就可以確保在設定值附近具有良好的調節效果。同時，Ma數在該階段始終處于閉環調節狀態，從而可確保Ma數的調節精度。

(2)

圖2 定Ma數連續變總壓示意圖

Fig.2 Sketch of continuously adjusting total pressure at fixing Mach number

2.2 數據處理

顫振試驗數據處理的目的是獲取顫振亞臨界范圍的模態參數或特征變量，根據振動系統穩定性原理或速壓與振動能量的關系構造穩定性判據，進而外插獲取顫振臨界點。本文發展的連續變速壓顫振試驗數據處理方法分為以下3個步驟：

(1) 數據預處理。連續變速壓顫振試驗數據的模態參數是連續變化的。因此，在計算數據選取時，既不是分段截取(見圖3(a))，也不是連續整段全選，而是采用前后搭接分段截取的方式(見圖3(b))，也就是說用于計算的每段數據都具有一定量的重疊，計算后一段的參數時也用到了前面的數據信息。這樣一來，既可以增加計算的樣本量，保證結果具有較高的精度，又能反映出系統的時變特性[9]。

圖3 數據選取策略

(2) 顫振邊界的穩定性參數構造。能夠用于指示顫振臨界點的穩定性參數有很多，比如阻尼比、Routh判據和Jury判據等等[10]。通過實踐應用證明，NASA發展的Pick-Hold方法具有較高的魯棒性和可靠性。下文簡單描述其原理：

當處于氣流中的彈性系統(例如機翼)受到紊流激勵時，對于系統的振幅A來說，可以用一個簡單的表達式來描述：

(3)

式中：Q是廣義氣動力，它是馬赫數與簡縮頻率的函數；V是氣流速度；ρ是氣流密度；下標f、t分別代指顫振與紊流。等式兩邊分別取倒數得到：

(4)

(3) 外插顫振臨界點。表面上看，峰值倒數呈隨機分布，但實際上可近似認為是正態分布的。于是，基于數理統計理論，將峰值倒數與其平均值的偏差作為隨機變量，設定該正態分布的置信區間，擯棄置信區間以外散布度較大的數據，再次擬合峰值倒數隨速壓變化的曲線。若數據散布度仍較大，可重復以上步驟直至合理為止。最后，根據擬合曲線外插即可獲取顫振臨界速壓。

3 風洞試驗驗證

3.1 流場調試結果分析

連續變速壓顫振試驗流場控制技術要求如下：

(1)Ma數變化平穩，波動量小，σM<0.005；

(2) 單車次總壓跨度可達150kPa以上，使模型能從較弱的平穩振動過渡到較劇烈的亞臨界振動，為亞臨界預測提供所需的數據樣本；

(3) 在起動過程中，速壓緩慢平滑上升；關車時，速壓迅速降低至0；

(4) 流場建立后，速壓線性勻速爬升，且變化率可調；速壓超調量盡可能小，σq<0.1kPa。

圖4給出了FL-26風洞連續變速壓工況時的典型流場參數控制結果，圖中陰影部分曲線是流場正式建立后的區域。為了指示出試驗數據的有效范圍，流場控制時將在流場穩定與關車前都給出判穩信號。可以看出，在吹風過程中，速壓曲線規律性較好，速壓線性勻速增大，沒有超調情況出現；Ma數控制平穩，曲線的波動量很小，σM<0.003，達到了期望的流場技術指標要求。

圖4 典型Ma數的連續變速壓流場調試結果

Fig.4 Flow field test data of continuously adjusting dynamic pressure at typical Mach number

3.2 顫振試驗結果分析

(1) 階梯與連續變速壓試驗結果的對比

圖5給出了FL-26風洞大展弦比超臨界機翼連續與階梯變速壓顫振試驗工況下典型試驗車次的顫振邊界亞臨界預測對比結果。

可以看出，在對應的有效速壓范圍內，2種工況下的峰值倒數變化趨勢是一致的，線性擬合外插的結果相差不大。總體來看，階梯試驗結果的規律性相對更好一些，連續試驗結果的數據點更多，信息量相對更豐富，且隨著速壓逐漸進入顫振亞臨界范圍，峰值倒數的散布度逐漸減小，規律性也變得更好。因此，連續試驗結果峰值倒數的數據點反映了模型顫振特性隨速壓的變化趨勢，可以給出與階梯試驗本質上一致的結果。

(2) 速壓變化率對試驗結果的影響

在確保試驗安全的前提下，為了縮短吹風時間，減少耗氣量，顫振試驗時希望速壓變化率盡可能大。為了驗證速壓變化率對試驗結果的影響，圖6給出了不同速壓變化率情況下的顫振邊界亞臨界預測結果。

圖5 階梯與連續變速壓試驗結果的對比(Ma=0.7)

Fig.5 Comparison of test results with adjusting dynamic pressure on step and continuation (Ma=0.7)

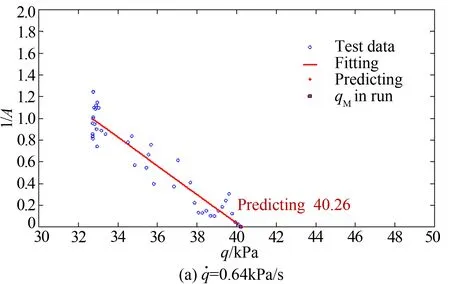
圖6 速壓變化率影響(Ma=0.76)

從理論上來說，只要試驗速壓進入了顫振亞臨界范圍，速壓變化率對預測結果的影響會很小。從圖6可以看出，實際情況也與理論相符，圖6中(a)與(b)的變化趨勢一致，偏差小于1.4%。其中，速壓變化率較大時的顫振臨界速壓略有降低。不難理解，當速壓變化較快時，流固耦合作用更強，模型振動更加劇烈，可能導致顫振提前發生。因此，出于安全角度考慮，實際吹風時的速壓變化率不宜過大。

(3) 吹風逼近程度對預測結果的影響

在高速風洞顫振試驗過程中，為了避免發生顫振損壞模型及風洞設備，當試驗速壓接近顫振臨界點時，一般希望盡早關車。但是，從預測準確性的角度來說，又要求試驗速壓盡可能趨近顫振臨界點。這2者的要求是相互矛盾的。因此，為了同時確保試驗的安全與結果的可靠，在實踐中是要求試驗速壓必須進入顫振亞臨界范圍但又不能達到顫振臨界點。然而，在試驗前，即使是顫振亞臨界范圍，也是難以準確獲知的，只能根據模型的設計結果來預估。因此，若要可靠地預測顫振臨界點，數據處理方法就不應該對試驗速壓的逼近程度過于敏感，否則，亞臨界預測便失去了應有的意義。為了檢驗數據處理方法的魯棒性，利用同一試驗車次的不同速壓段分別進行計算，圖7給出了相應的計算結果(qM表示每車次試驗過程中吹風速壓的最大值)。可以看出，盡管圖中所示的試驗速壓逼近程度不一樣，但是最終的預測結果在規律性和數值上是基本一致的。

圖7 試驗速壓逼近程度對結果的影響(Ma=0.7)

3.3 連續與階梯試驗的耗氣量對比

對于高速暫沖式風洞來說，采用傳統的階梯變速壓顫振試驗方法，其耗氣量是驚人的，通常數10倍于常規測力測壓試驗。發展連續變速壓顫振試驗技術的主要目的之一就是節省耗氣量，下文通過對比分析來說明其效果。圖8給出了典型狀態下階梯與連續變速壓顫振試驗工況下的流場參數變化情況，同時也反映了其各自的耗氣量情況。根據計算，在Ma=0.7時，為了獲取研究模型的顫振點，階梯變速壓顫振試驗工況下的耗氣量為3.05pA(pA表示氣源系統的壓力降低1個大氣壓時所對應的耗氣量)，連續變速壓顫振試驗工況下的耗氣量為1.87pA，節省耗氣量將近40%。對于大型跨聲速風洞來說，其經濟性可見一斑。這主要是由于連續試驗工況沒有了中間的速壓階梯，在相同的速壓范圍內，吹風時間縮短，總耗氣量必定減少。

圖8 2.4m風洞階梯與連續變速壓試驗的耗氣量對比(Ma=0.7)

Fig.8 Comparison of gas consumption in 2.4m wind tunnel with adjusting dynamic pressure on step and continuation

4 結 論

以FL-26跨聲速風洞為研究平臺，建立適用于大型高速暫沖式風洞工程實用的連續變速壓顫振試驗技術，使用大展弦比超臨界機翼顫振模型進行了實際考核驗證，并對試驗結果進行了對比分析。得到了以下結論：

(1) 針對FL-26風洞設計的基于運動函數的定Ma數線性變總壓控制策略，實現了流場的定Ma數連續變速壓控制目標，Ma數控制精度達到0.005以內，且試驗過程中速壓沒有超調情況出現，滿足了高速風洞顫振試驗的技術指標要求。

(2) 采用Pick-Hold方法構建顫振邊界的亞臨

界預測判據，基于數理統計理論的參數估計方法來減小預測判據的散布度，從而提高顫振邊界亞臨界預測準確性。

(3) 在高速暫沖式風洞采用連續變速壓顫振試驗技術可以取得與階梯變速壓顫振試驗技術一致的結果，且魯棒性較高，具備了工程實用化水平。

(4) 在高速暫沖式風洞采用連續變速壓顫振試驗技術時耗氣量大大降低，經濟效益更加顯著。

[1]Garrick I E, Reed W H. Historical Development of Aircraft Flutter[J]. Journal of Aircraft, 1981, 18(11): 981-994.

[2] Charles L Ruhlin, Judith J Watson. Evaluation of four subcritical response methods for on-line prediction of flutter onset in wind-tunnel tests[R]. AIAA 1982-82-0644: 94-101.

[3] Robert V, Doggett J. Some observations on the houbolt-rainey and peak-hold methods of flutter onset prediction[R]. NASA TM-102745, 1990: 1-10.

[4] William D Anderson. The aeroelastic design and testing of the F/A-22[C]. 2005 USAF Aircraft Structural Integrity Program Conference, Memphis, Tennessee, 2005.

[5] Torii H, Matsuzaki Y. Flutter margin evaluation in discretetime system[R]. AIAA 1998-98-1724: 229-236.

[6] Torii H, Matsuzaki Y. Application of a new aeroelastic stability criterion for real-time flutter prediction[R]. AIAA-1999-99-1351: 1314-1320.

[7] Robert Walker, Naren Gupta. Real-time flutter analysis[R]. NASA Contractor Report, 170412, 1984.

[8] 盧奇正. 風洞模型顫振試驗技術[R]. CARDC-2, 1996.

[9] 郭洪濤, 劉靖, 呂彬彬, 等. 連續變速壓顫振試驗數據處理方法研究[C]. 第十四屆系統仿真會議, 2012, 7: 888-893.

Guo Hongtao, Liu Jing, Lyu Binbin, et al. Investigation on data processing method for flutter test with continuously-varying dynamic pressure[C]. The 14th System Simulation Technology & Application, 2012, 7: 839-843.

[10] 郭洪濤, 路波, 呂彬彬, 等. 面向紊流激勵響應的顫振亞臨界預測方法[C]. 第十三屆系統仿真會議, 2011, 8: 888-893.

Guo Hongtao, Lu Bo, Lyu Binbin, et al. A subcritical prediction of flutter onset for excitation response based on airstream turbulence[C]. The 13th System Simulation Technology & Application, 2011, 8: 888-893.

(編輯：楊 娟)

Research on flutter test technology of continuously adjusting dynamical pressure in high-speed wind tunnel

Guo Hongtao1,2,*, Yan Yu2, Yu Li2, Lyu Binbin2, Du Ning2

(1. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China; 2. High Speed Aerodynamics Research Institute, China Aerodynamics Research and Development Center, Mianyang Sichuan 622763, China)

According to the defects shown in the flutter tests of stepped adjusting dynamical pressure in high speed intermittent wind tunnel, such as: long testing time, high gas consumption, and short acceptable life of testing models, researches on flutter test technology of continuously adjusting dynamical pressure in high-speed intermittent wind tunnels are conducted. Technical problems of flutter test data processing and wind tunnel flow controlling have mainly been solved. The specific approaches are: in the 2.4m×2.4m blow off transonic wind tunnel, fixed Mach number and linear varying total pressure controlling strategies based on movement function are presented, and thus the flow controlling goal of fixed Mach number continuously adjusting dynamical pressure is achieved. The controlling uncertainty of Mach number reaches less than 0.005 without deviation of dynamical pressure. The Pick-Hold method is adopted to set up the subcritical prediction criterion in flutter boundary; according to the characteristic that the reciprocal of predicting criterion is close to the normal distribution, a parameter estimation method based on the mathematical statistics theory can be used to reduce the diffusive sampling of the prediction criterion and then the accuracy of the subcritical prediction of flutter boundary can be increased. The results of wind tunnel verification test show that the flutter test results of continuously adjusting dynamical pressure is in consistent to that of stepped adjusting dynamical pressure, and the test technology has reached engineering practical levels; besides, the gas consumption is greatly reduced by using flutter test technology of continuously adjusting dynamical pressure, and thus it also has good economic benefits.

flutter;aero-elasticity;wind tunnel test;test technology;flow controlling

1672-9897(2015)05-0072-06

10.11729/syltlx20150061

2015-04-26;

2015-06-10

GuoHT,YanY,YuL,etal.Researchonfluttertesttechnologyofcontinuouslyadjustingdynamicalpressureinhigh-speedwindtunnel.JournalofExperimentsinFluidMechanics, 2015, 29(5): 72-77. 郭洪濤, 閆 昱, 余 立, 等. 高速風洞連續變速壓顫振試驗技術研究. 實驗流體力學, 2015, 29(5): 72-77.

V215.3+4

A

郭洪濤(1980-)，男，四川南部人，高級工程師，博士研究生。研究方向：飛行器氣動彈性力學。通信地址：四川省北川縣永安鎮101信箱202室(622761)。E-mail：ght1998@126.com

*通信作者 E-mail: ght1998@126.com