基于蒙特卡洛法的探測傳感器基準誤差仿真

侯玉宏

摘 要： 在簡要介紹探測傳感器發展趨勢基礎上，分析了目前探測傳感器精度評估和基準獲取方法，并探討該基準獲取方法的原理誤差，提出利用蒙特卡洛方法對探測傳感器基準誤差進行分析的方法，并利用該方法對探測傳感器的精度水平、影響因素、坐標不重合等情況進行了仿真分析。仿真結果為探測傳感器精度評估方法提供了理論依據，對未來探測傳感器基準獲取技術的改進具有指導意義。

關鍵詞： 探測傳感器； 蒙特卡洛法； 基準誤差； 仿真分析

中圖分類號： TN06?34； V217+.1 文獻標識碼： A 文章編號： 1004?373X（2015）12?0098?04

隨著高新技術的不斷發展，運用微米、毫米波、電視、紅外、激光、電子支援措施以及電子情報技術等覆蓋寬廣頻段的各種有源和無源探測傳感器層出不窮，另外利用數據融合技術實現綜合探測更是探測傳感器發展的方向，當前探測傳感器精度評判的方法能否滿足未來探測傳感器精度不斷提高的要求，影響探測傳感器基準數據精度的因素有哪些，都是探測傳感器設計定型試飛過程中必須面對和解決的問題。針對上述問題，本文利用蒙特卡洛法對上述問題從理論角度進行了分析仿真。

1 探測傳感器試飛評估方法及影響基準精度的

因素

無論探測傳感器技術如何發展，其目的不外乎是向飛行員提供更加準確、可靠的目標位置信息，基于該出發點可以說明探測傳感器精度評價方法原理應該是不會變的，就是利用更加精確的探測傳感器基準信息與探測傳感器輸出數據在統一時基條件求差，計算并統計給出探測傳感器的精度結果。

目前獲取探測傳感器基準的方法是利用飛行后載機和目標機的差分GPS位置、速度數據以及載機姿態數據，通過坐標變換計算輸出探測傳感器的基準數據，具體為已知載機大地坐標（B0，L0，h0），載機速度（VE1，VN1，VU1），載機姿態（pitch，roll，head），目標機大地坐標（B1，L1，h1），目標機速度（VE2，VN2，VU2）求解目標機在載機機體坐標系下的[（α]，[λ]，R，V，VE，VN，VU）過程。其中[α]是方位角，[λ]是俯仰角，R是距離，V為目標徑向速度，VE是東向速度，VN是北向速度，VU為天向速度，坐標變換過程如圖1所示。

圖1 探測傳感器基準數據獲取計算過程

從當前探測傳感器基準獲取過程可知，探測傳感器基準數據是假定載機GPS天線安裝位置即是飛機機體坐標系，由此可以推出影響探測傳感器基準輸出精度的原因有兩個方面，一方面是計算機體坐標系與實際機體坐標系存在的誤差對基準輸出造成的誤差，另一方面是測得的載機、目標機位置、速度、姿態等參數的測量誤差對基準輸出造成的誤差。

2 基于蒙特卡洛法的基準誤差分析方法

要分析探測傳感器基準獲取過程的坐標轉換中各參數對測量結果的影響，首先要知道誤差傳遞關系，誤差傳遞的計算方法很多，如全差分法、絕對值法、均方誤差法和蒙特卡羅法，探測傳感器基準數據的獲取過程就是若干坐標變換的過程，需要多個矩陣相乘，用蒙特卡洛統計試驗的方法分析最為適合。

2.1 蒙特卡羅仿真方法簡介

蒙特卡羅（Monte?Carlo）仿真方法亦稱概率仿真方法，有時也稱作隨機抽樣技術或統計試驗方法。它是一種通過隨機變量的統計試驗、隨機仿真來求解數學物理、工程技術問題近似解的數值方法。蒙特卡羅法的理論基礎來自概率論的兩個基本定理[1]：

大數定理：設[x1，x2，…，xn]是n個獨立的隨機變量，若它們來自同一母體，有相同的分布，且有相同的有限的均值和方差，分別用[μ]和[σ2]來表示，則對于任意的[ε]>0有：

[limn→∞P1ni=1nxi-μ≥ε=0] （1）

伯努利定理：若隨機事件A發生的概率為P（A），在n次獨立實驗中，事件A發生的頻數為m，頻率為W（A）=[mn]，則對于任意的ε>0有：

[limn→∞Pmn-P（A）<ε=1] （2）

蒙特卡羅法從同一母體中抽出簡單子樣來做抽樣試驗，由上述兩個定理可知，當n足夠大時，前式以概率1收斂于[μ]；頻率[mn]以概率收斂于P（A）。因此從理論上講，這種方法的應用限制幾乎沒有。

2.2 蒙特卡洛方法仿真思想及其步驟

用蒙特卡洛仿真方法求解問題時，應建立一個概率模型，使待解問題與此概率模型相聯系，然后通過隨機試驗求得某些統計特征值作為待解問題的近似解。當所求解的問題是某個事件出現的概率時，可以通過抽樣試驗的方法得到這種事件出現的概率，把它作為問題的近似解，這就是蒙特卡羅仿真方法的基本思想。

在進行蒙特卡羅仿真分析時，仿真步驟可分為構造概率模型、實現已知概率分布抽樣、建立各種統計量的估計，具體為：

（1） 構造概率模型：即根據所要研究的數學物理問題提取出一個隨機性質的概率模型；

（2） 實現已知概率分布的抽樣：即對這個概率模型中的隨機變量進行抽樣，得到該隨機變量的一個試驗樣本，探測傳感器基準數據誤差與多種因素有關，包括參數的真值和其相應的誤差；

（3） 建立各種統計量的估計：即對抽樣數據進行統計分析，得出需要求解的問題的近似解，作為原數學物理問題的解。

2.3 基于蒙特卡洛法的探測傳感器基準仿真模型構建

根據蒙特卡洛法的基本原理，其數學模型可表示為：

[ΔY=F（x1+Δx1，x2+Δx2，…，xn+Δxn）-F（x1，x2，…，xn）] （3）

式中：xi為坐標轉換過程中各參數的測量值；[Δx]為其測量誤差；F為探測傳感器基準獲取過程。

若將探測傳感器基準計算過程表示為：

[[α，λ，R，V，VE，VN，VU]=P（X）] （4）

則可由式（3）和式（4）得到基準誤差模型為[2?5]：

[[Δα，Δλ，ΔR，ΔV，ΔVE，ΔVN，ΔVU]=P（X+ΔX）-P（X）] （5）

式中：P表示探測傳感器基準獲取坐標轉換過程；X表示探測傳感器基準獲取轉換過程中用到的參數，包括：（B0，L0，h0）：目標點的大地坐標（緯度，經度，大地高）；（B1，L1，h1）：載機的大地坐標（緯度，經度，大地高）；（yaw，pitch，roll）：載機姿態角（航向，俯仰，橫滾）；（VE1，VN1，VU1）：載機三向速度（東向速度，北向速度，天向速度）；（VE2，VN2，VU2）：目標三向速度（東向速度，北向速度，天向速度）；[Δα，Δλ，ΔR，ΔV，ΔVE，ΔVN，ΔVU]為探測傳感器基準數據的誤差，[ΔX]為坐標轉換過程中的相應參數的誤差。

3 探測傳感器基準誤差仿真及分析

3.1 探測傳感器基準精度水平仿真分析

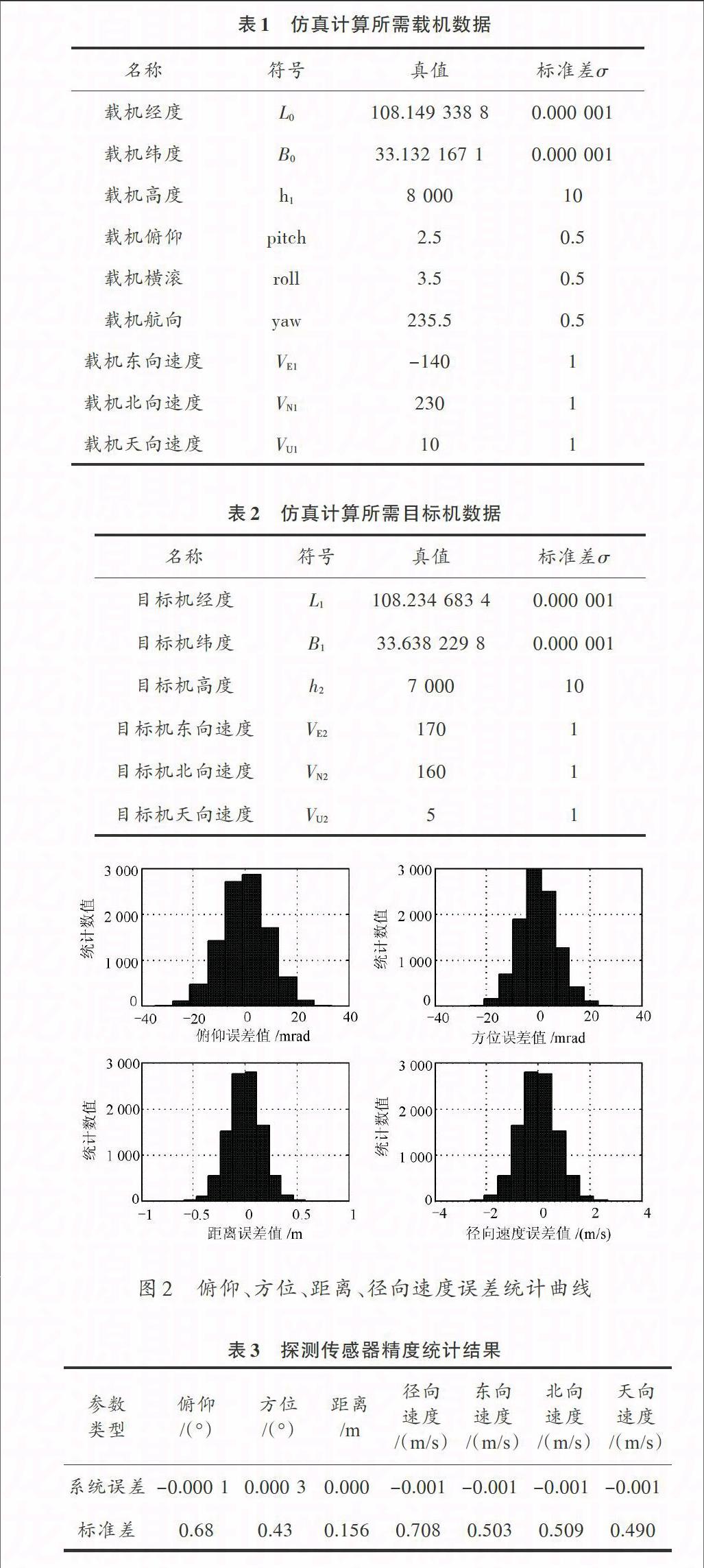
根據測量參數概率分布的特點，可將測量參數構造為服從ΔX～N（0，σ）的正態分布誤差數據，采樣點數為10 000，現假設載機與目標機在某次試飛中某瞬間測量數據和傳感器精度如表1，表2所示。

利用蒙特卡洛方法進行仿真，得到基準數據誤差統計曲線如圖2所示。可看出基準數據誤差分布也服從μ=0的正態分布。按照同樣方法在探測傳感器精度不變情況下，改變兩機距離，分析探測傳感器基準數據輸出結果，通過分析可知探測傳感器基準輸出精度與兩機距離無關，精度水平如表3所示。

3.2 探測傳感器影響因素仿真分析

由式（5）可知影響探測傳感器基準數據精度的因素有姿態、位置、速度精度，為確定各個因素對基準數據輸出的影響需要固定某些參數測量精度不變，而逐漸改變輸出結果與變化因素的關系曲線。從而找出影響基準數據精度的主要因素，由于精度計算與兩機距離無關，因此選用表1，表2為基本參數，當某組參數逐漸變差情況下，統計計算與探測傳感器基準輸出標準差的對應關系，分析結果如下：

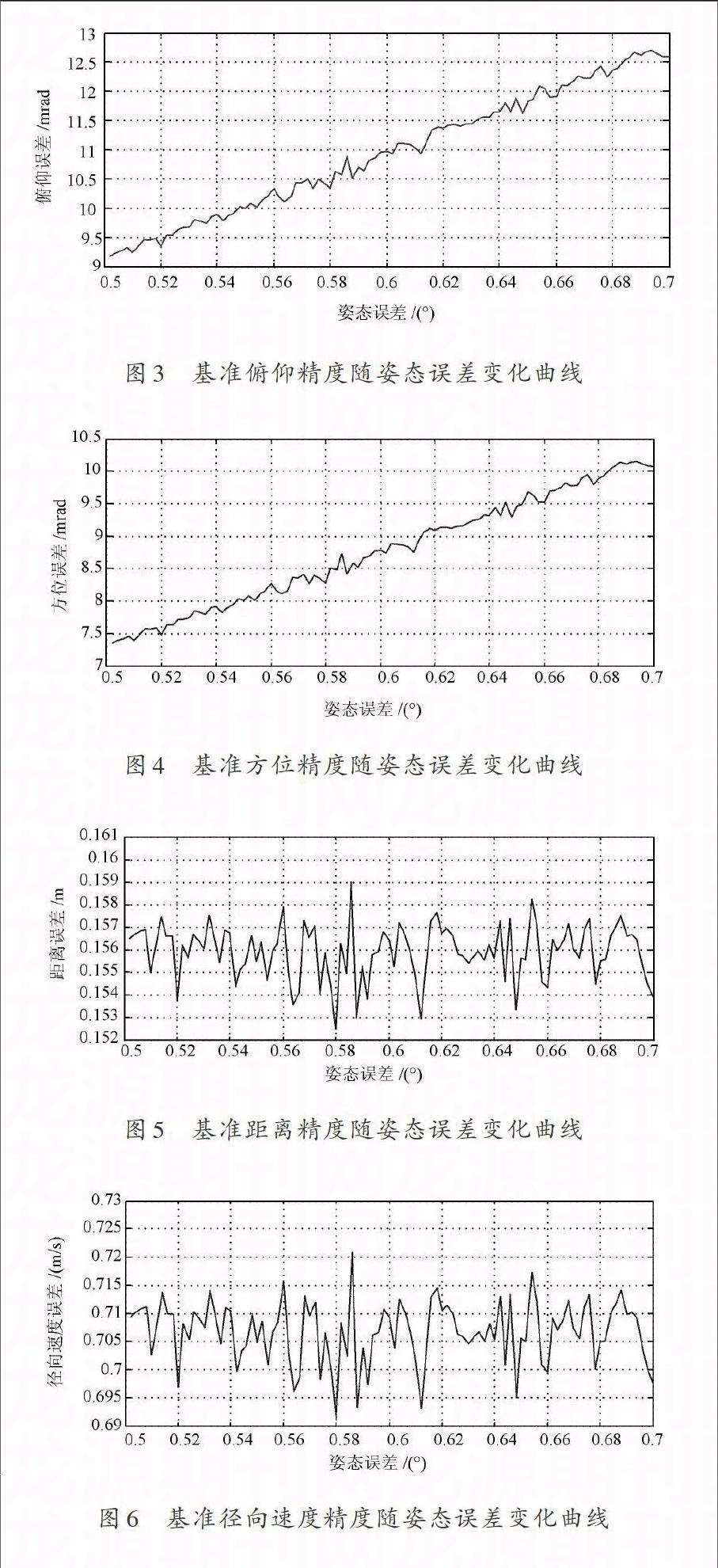
（1） 姿態精度（Δyaw，Δpitch，Δroll）對輸出精度的影響，如圖3～圖6所示。

由圖3～圖6可知，姿態精度主要影響基準輸出的測角精度，且隨姿態精度的變差而變差，對距離、速度精度影響較小。

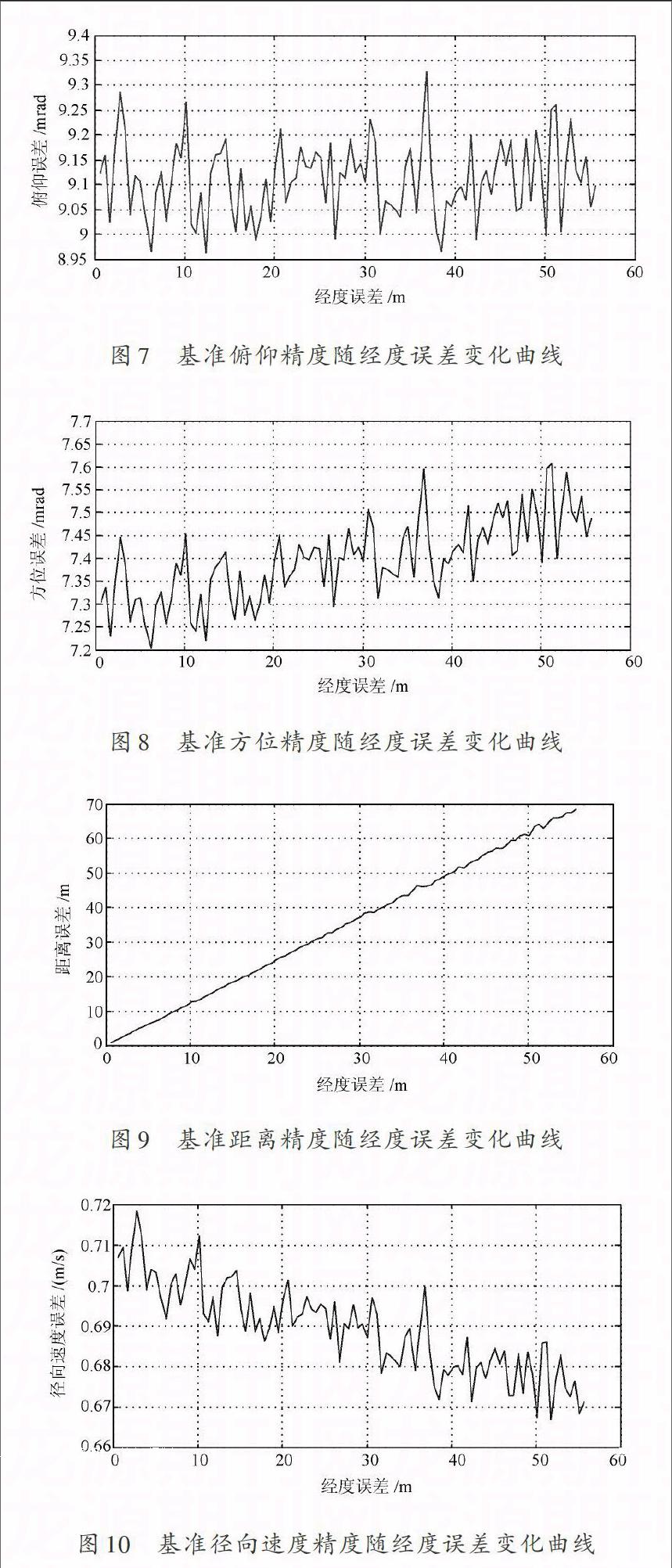
（2） 載機位置精度（ΔB0，ΔL0）對輸出精度的影響，如圖7～圖10所示。

由圖7～圖10可知，載機位置精度主要影響探測傳感器基準輸出的測距精度，且隨位置精度的變差而變差，對探測傳感器基準輸出測角和測速精度影響較小。

（3） 載機速度精度（ΔVE1，ΔVN1，ΔVU1）對輸出精度的影響如圖11，圖12所示。

由圖11，圖12可知，載機速度精度主要影響探測傳感器基準輸出的測速精度，且隨測速精度的變差而變差，對探測傳感器基準輸出測角、測距精度影響較小。

3.3 計算機體坐標系與實際機體系存在差異對基準輸出影響分析

假設GPS測量點位置與載機實際機體坐標系原點位置偏差為（方位：-2.5°，俯仰：2°，距離：10 m），各參數精度水平可按表1，表2，統計不同距離情況下基準輸出精度結果。從統計結果看，在該假設條件下對基準輸出的標準差影響不大，主要影響基準輸出的系統誤差，在遠距條件下坐標不重合情況對精度影響可忽略，而當距離小于5 km后，俯仰和方位的系統誤差將迅速增大，以致不可忽略，需對探測傳感器輸出數據進行修正后才可用于探測傳感器的性能評價，基準輸出俯仰和方位系統誤差隨距離變化曲線如圖13，圖14所示。

4 結 語

利用蒙特卡洛方法分析了當前探測傳感器基準輸出的精度水平，分析了影響探測傳感器基準輸出精度的因素及不同因素對探測傳感器基準輸出數據精度的影響，以及當計算坐標系與實際機體坐標系存在差異情況下對探測傳感器基準輸出精度的影響，為當前探測傳感器精度評估及后續如何提高探測傳感器基準精度提供了理論依據，另外，提供了一種利用數學模型對試飛結果進行預測、仿真模擬的研究思路，對于未來數字化試飛技術的發展具有一定的參考意義。

參考文獻

[1] 王姝.機載光電測量系統引導及定位技術研究[D].長春：長春理工大學，2007.

[2] 朱本仁.蒙特卡羅方法引論[M].濟南：山東大學出版社，2002.

[3] 毛英泰.誤差理論與精度分析[M].北京：國防工業出版社，2009.

[4] 左安元，劉剛.一種機載定位坐標轉換方法誤差分析及仿真[J].電視技術，2006（6）：58?62.

[5] TAN He?ping， SHUAI Yong， XIA Xin?lin， et al. Reliability of stray light calculation code using the Monte Carlo method [J]. Optical Engineering， 2005， 44（2）： 023001.

[6] 魏強，李雨.機載任務電子系統總體布局優化設計[J].現代電子技術，2014，37（21）：124?126.