光刻機運動平臺系統的模型辨識

范文超 陳興林 王 斌 魏 凱

(哈爾濱工業大學航天學院，黑龍江 哈爾濱 150001)

光刻機運動平臺系統的模型辨識

范文超 陳興林 王 斌 魏 凱

(哈爾濱工業大學航天學院，黑龍江 哈爾濱 150001)

針對機械諧振對超精密光刻系統的影響，對包含有機械諧振的光刻機宏微運動平臺進行辨識來抑制機械諧振。首先建立單自由度宏微耦合運動模型和諧振模型，然后基于遞階辨識原理對機械諧振模型進行分段辨識，最后基于諧振模型設計陷波器，抑制機械諧振。試驗結果證明,該方法有效抑制了宏微平臺的機械諧振，大幅提高了系統的動態響應性能。

光刻機 宏微耦合模型 機械諧振 遞階辨識 動態響應性能

0 引言

近年來，隨著半導體加工領域的發展，超精密運動控制技術越來越受到重視。光刻機是一種光機電一體化的超精密制造設備，其中控制系統決定了光刻機的總體性能。在超精密光刻領域，諧振會影響精密運動系統的穩定性。光刻機系統要求的帶寬很高，而機械諧振頻率又比較低，導致系統固有機械諧振頻率比系統的帶寬小，噪聲極易引起系統整機諧振，使系統變得不穩定[1]。

基于上述問題，本文采用基于遞階辨識原理的諧振模型辨識策略，對精密運動平臺的機械諧振模型進行了參數辨識，建立了一個能夠反映系統高頻諧振特性的數學模型，并基于諧振模型設計了陷波器。試驗結果表明，該方法有效抑制了微動臺和宏動臺的機械諧振。

1 光刻機平臺單自由度數學模型

1.1 光刻機雙工件臺結構

光刻機雙工件臺是由平衡質量塊、宏動臺和微動臺3部分組成的。由氣浮支撐面將它們組合在一起，進行光刻工作[2]。

平衡質量塊由4個氣足提供支撐力，使其氣浮于底座之上，不與雙工件臺底座接觸，這樣可以起到減小摩擦和隔振的作用，大大提高光刻機的精度。

宏動臺的兩端是直線電機的動子，對于宏動臺采用雙邊驅動的策略，其執行機構是永磁直線電機(permanent magnet linear motor，PMLM)。

微動臺的執行機構是音圈電機(voice coil motor，VCM)。整個微動臺的底部有氣足，同樣可以起到減小摩擦和隔振的作用，保證了微動臺的穩定性。微動臺的頂部是一個具有6個自由度的平臺，其上放置硅片，安裝有定位裝置，可以用雙頻響激光干涉儀來檢查微動臺的位置[3]。

1.2 直線電機和音圈電機數學模型

宏動臺由永磁直線電機驅動，永磁直線電機的模型在轉子dq0旋轉坐標系中可以表達為:

(1)

式中：ud、uq為電機定子電壓；id、iq為電機定子電流；Ld、Lq為電樞電感，在電樞中相等；λd、λq為磁鏈；Rs為電樞電阻；Ifd為勵磁電流；Lmd為q軸的互感系數；p為極對數。

電磁推力方程為:

f=K[LmdIfdiq+(Ld-Lq)idiq]

(2)

對于固定安裝好的永磁直線電機來說，Lmd和Ifd是一個常數，永磁直線電機通常采用矢量控制方法，id=0，所以d軸的磁鏈λd是固定的，僅iq提供推力。這樣，電磁推力直接正比于iq，iq是受閉環控制的。這時式(2)推力方程為:

f=KLmdIfdiq=Kfiq

(3)

式中：Kf為電機推力系數。

永磁直線電機的輸出力fe與q軸電流iq成正比，控制q軸的電流即可控制永磁直線電機輸出力。

取反電動勢系數Ke=pLmdIfd，i=iq，u=uq，那么推力方程為f=Kfi，則可以得到如下所示的電壓方程：

(4)

根據牛頓第二定律，忽略電機擾動力等阻力，永磁直線電機帶負載運動方程為：

f=ma

(5)

式中：f為永磁直線電機輸出的力；a為直線電機加速度。

這樣可以提供的模型如下：

(6)

結合式(6)，可以得到直線電機的傳遞函數框圖如圖1所示。為了區分音圈電機和直線電機，各參數添加下標v表示音圈電機相關參數，添加下標l表示直線電機相關參數。音圈電機模型如圖2所示。

圖1 直線電機模型

圖2 音圈電機模型

由于電氣時間常數遠小于機械時間常數，電氣瞬態響應延遲可以被忽略，那么新的直線電機模型如下：

(7)

同理，建立音圈電機模型：

(8)

1.3 單自由度宏微耦合運動模型

在超精密控制領域，通常采用宏動臺來實現高速度長行程運動，采用微動臺實現小行程和高精度性能。宏微運動控制結構簡化后的模型如圖3所示。

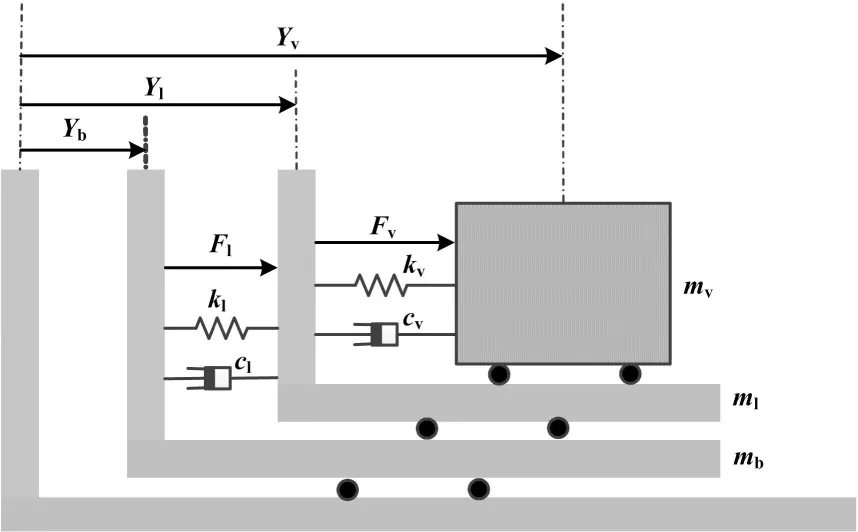
圖3 宏微耦合力學模型

微動臺、宏動臺以及平衡質量塊的位移參考位置是相對于地面靜止的測量框架。在對硅片臺上的晶圓進行掃描過程中，平衡質量塊具有和宏動臺相反的運動方向，將平衡質量塊和宏動臺之間視為無外力作用的整體。設初始位置均為零，建立力學方程和位移關系為：

(9)

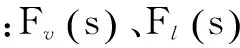
平臺采用氣浮導軌支撐，可以忽略其阻尼系數cv、cl和剛度系數kv、kl，那么有：

(10)

精密運動平臺y向宏微耦合的模型如圖4所示。

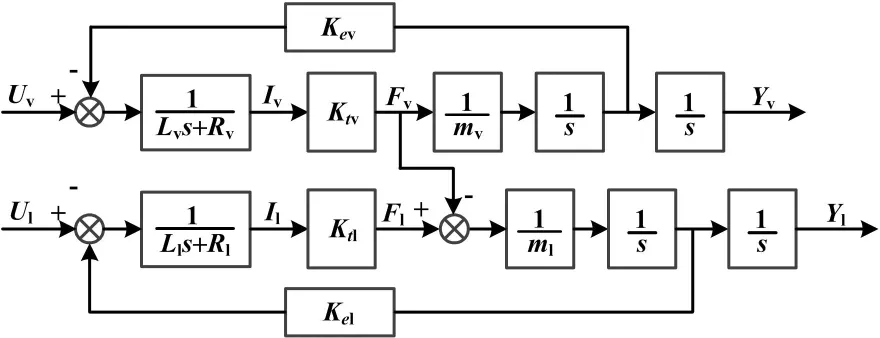
圖4 宏微耦合等效框圖

建立精密運動平臺的y向宏微耦合模型可以表示如下：

(11)

即：

(12)

實際中的精密運動平臺參數如表1所示。

表1 電機參數參考值

根據表1，計算得到如下數值：Kev=42.218 8，Kel=43.399 4，Rvmv/Kfv=3.087 8，Rlmv/Kfl=0.539 1，Rlml/Kfl=1.290 9。

所以，精密運動平臺的y向宏微耦合模型為：

2 機械諧振模型及參數遞階辨識

2.1 機械諧振模型

因為精密運動平臺不是理想的剛體，機械諧振不可避免地存在于精密運動系統中，這是機電耦合的結果。如果將系統中的執行元件視為理想的剛體，對電機進行建模的過程中，常常將諧振模態當做系統未建模動態來考慮[4-6]。系統的諧振頻率ωm較高，作為未建模動態來處理時，那么系統的帶寬應該限制為：

ωBW<ωm/5

(13)

但是，如果系統的帶寬要求很高，而機械諧振頻率又比較低，那么如果兩者很接近，或者系統固有機械諧振頻率比系統的帶寬小，噪聲極易引起系統整機諧振，反饋又會加劇諧振，這樣可能會使系統變得不穩定[7]。

被控對象包含機械諧振時，其開環Bode圖在穿越0 dB線以后又回升到了0 dB線上，會使系統動態指標偏離理想值，甚至使系統穩定性變差或者不穩定。所以，抑制精密運動平臺的機械諧振是十分重要的。

通過掃頻試驗，可以得到精密運動平臺的頻率特性數據。由數據可以看出，在低頻頻率段時跟理想模型是相符的，但是往往在較高頻率段的數據已經和理想模型出現了很大的差異。顯然，對于一個已經加工好的精密機械系統，改進機械系統結構是一個很費成本和不現實的情況，而精密運動系統又不能忽略諧振的影響，所以一般會先嘗試從伺服控制系統設計的角度解決這個問題[8]。

對于精密運動平臺的機械諧振來說，可以將其表示為許多個二階環節串聯的模式。由調試經驗可知，諧振模型可以表示為二階環節：

(14)

式中：ωc為系統諧振的中心頻率；a、b為大于0的浮點數。

當a>b時，諧振被稱為正諧振；a

2.2 參數遞階辨識

在工程中，常用遞階辨識來建立系統的模型。遞階辨識就是將復雜系統分為一個個微小子模型，通過參數優化等方法使模型和真實系統之間的誤差變得極小，確定模型的參數。

對于系統的高頻域模型辨識，往往采用遞階辨識方法，將模型分為各個子模型：

G(jω)=Go(jω)Gr1(jω)Gr2(jω)…Grn(jω)

(15)

式中：Go(jω)為低頻段理想模型，Gr1(jω)，Gr2(jω)，Gr3(jω)，…，Grn(jω)為高頻段機械諧振模型。

然后再對每個高頻段機械諧振模型的參數進行分段辨識。具體方法是先從全頻率數據中修正掉低頻段理想模型，基于修正后的模型與實際平臺數據之間的誤差來逐次確定其他高頻部分的參數。

3 精密運動平臺模型辨識及有效性驗證試驗

本章在已知精密運動平臺單自由度耦合模型結構的情況下，基于遞階辨識原理，對精密運動平臺的機械諧振模型進行了參數辨識，建立了一個能夠反映系統高頻諧振特性的數學模型，并基于諧振模型設計陷波器，有利于控制系統的設計[10-12]。

3.1 宏動臺機械諧振辨識及其抑制方法

3.1.1 宏動臺機械諧振辨識

通過掃頻試驗、數據插值和濾波、相關分析算法計算幅值比和相角差，最終得到宏動臺的開環頻率特性G(jω)。從系統開環頻率特性中剔除掉已知的低頻理論模型的頻率特性：

(16)

剩下的頻率特性為各諧振的頻率響應：

(17)

宏動臺機械諧振頻率特性如圖5所示。

圖5 宏動臺機械諧振頻率特性

由圖5可以看出，機械諧振模型：

(18)

其幅值特性和相頻特性分別為：

可知系統第一個諧振頻率在90 Hz和100 Hz之間，且是負諧振，a

(19)

辨識結果為：

(20)

修正第一個諧振模型后的頻率特性如圖6所示。

圖6 修正第一個諧振模型后的頻率特性

再按照同樣的方法進行參數辨識，依次得到系統中較為明顯的諧振模型:

(21)

(22)

(23)

3.1.2 宏動臺機械諧振的抑制方法

本文在辨識出機械諧振模型的基礎上，采用加陷波器的方案來抑制諧振。陷波器是一種帶寬很窄的帶阻濾波器。理想情況下，陷波器只有一個阻帶頻率點，采用其可以消除系統中該頻率點處的分量，其他頻率的分量不受影響，故可以用來消除機械諧振，從而拓展系統的帶寬。已知系統機械諧振模型為:

(24)

那么相對應的，可以設計陷波器抑制機械諧振:

(25)

根據其諧振模型，設計相對應的陷波器為

(26)

(27)

(28)

(29)

將陷波器和宏動臺串聯，則可以得到系統濾波前和濾波后不同的開環頻率特性。圖7是宏動臺的機械諧振特性和添加陷波器后的系統頻率特性。從圖7可以看出，系統的主要機械諧振得到了有效的抑制，這也證明辨識出的機械諧振模型是可信的。

圖7 補償前后的宏動臺頻率特性

3.2 微動臺機械諧振辨識及其抑制方法

3.2.1 微動臺機械諧振辨識

微動臺機械諧波辨識流程也是通過掃頻試驗、數據插值和濾波、相關分析算法計算幅值比和相角差，最終得到精密運動平臺微動臺的開環頻率特性G(jω)。從系統開環頻率特性中剔除掉已知的低頻理論模型的頻率特性，如圖8所示，該頻率特性即可以認為是微動臺的機械諧振特性。和宏動臺的機械諧振辨識一樣，基于遞階辨識原理對諧振模型分段辨識[13]。

圖8 微動臺的機械諧振特性

辨識出的兩個主要機械諧振模型為：

(30)

(31)

3.2.2 微動臺機械諧振的抑制方法

采用和宏動臺相同的方法來抑制微動臺的機械諧振，根據已經辨識出的微動臺的機械諧振模型，設計陷波器為:

(32)

(33)

按照示意將陷波器和微動臺模型串聯，則可以得到系統濾波前和濾波后不同的開環頻率特性。圖9是微動臺的機械諧振特性和添加陷波器后的系統頻率特性。從圖9可以看出，微動臺的主要機械諧振得到了有效的補償。這也證明了機械諧振模型的有效性，模型是可信的。

圖9 補償前后的微動臺頻率特性

4 結束語

本文首先研究了精密運動平臺的機械結構和工作原理，建立了其單自由度宏微耦合模型，得到了微動臺位移、宏動臺位移與直線電機、音圈電機輸入電壓之間的關系。由于理論建模中未考慮機械諧振，而機械諧振對光刻系統的帶寬影響是顯著的，所以本文建立了機械諧振模型。然后基于遞階辨識原理對諧振模型分段辨識，得到的就是機械諧振的頻率特性。基于辨識出的機械諧振模型，設計了相應的陷波器，有效抑制了微動臺和宏動臺的機械諧振。

[1] Yang C,Zhang Z,Zhao Q.The study on precision positioning system of two-dimensional platform based on high speed and large range[J].Precision Engineering,2010,34(3):640-646.

[2] Yang S M,Wang S C.Detection of resonance frequency in motion control systems[C]//Energy Conversion Congress and Exposition(ECCE),2013 IEEE，2013:3757-3761.

[3] 曾鳴,張東純,蘇寶庫.伺服轉臺高精度控制系統帶寬設計的探討[J].中國慣性技術學報,2001(2):56-60.

[4] 張尚盈,陳學東,趙慧，等.超精密工件臺的運動控制[J].華中科技大學學報：自然科學版,2008(10):009.

[5] 趙霞,姚郁.遞階辨識方法在轉臺伺服系統調試中的應用研究[J].控制理論與應用,2002,19(2):229-234.

[6] 董立立,趙益萍,梁林泉,等.機械優化設計理論方法研究綜述[J].機床與液壓,2010(15):114-119.

[7] Wang D,Ding R,Dong X.Iterative parameter estimation for a class of multivariable systems based on the hierarchical identification principle and the gradient search[J].Circuits, Systems, and Signal Processing,2012,31(6):2167-2177.

[8] 楊一博,尹文生,汪勁松,等.粗精動運動平臺的系統辨識激勵信號優化設計[J].機械工程學報,2010(9):165-170.

[9] 王帥,陳濤,李洪文,等.光電跟蹤伺服系統的頻率特性測試與模型辨識[J].光學精密工程,2009(1):78-84.

[10]Lei J,Luo X,Chen X,et al.Modeling and analysis of a 3-DOF Lorentz-force-driven planar motion stage for nanopositioning[J].Mechatronics,2010,20(5):553-565.

[11]Slocum A,Basaran M,Cortesi R,et al.Linear motion carriage with aerostatic bearings preloaded by inclined iron core linear electric motor[J].Precision Engineering,2003,27(4):382-394.

[12]Wang D,Ding R,Dong X.Iterative parameter estimation for a class of multivariable systems based on the hierarchical identification principle and the gradient search[J].Circuits,Systems,and Signal Processing,2012,31(6):2167-2177.

[13]Ha J L,Fung R F,Han C F.Optimization of an impact drive mechanism based on real-coded genetic algorithm[J].Sensors and Actuators A:Physical,2005,121(2):488-493.

Model Recognition of Lithography Motion Stage System

In view of the influence of the mechanical resonance on ultra-precision lithography system, the macro-micro motion stage containing mechanical resonance is recognized for suppressing the mechanical resonance. Firstly, the single degree of freedom(SDOF) macro-micro coupling model and resonance model are built, then, based on hierarchical recognition principle, the mechanical model is recognized segmentally, finally, the notch filter is designed based on resonance model for suppressing the mechanical resonance. The test results show that this method effectively suppresses the mechanical resonance of the macro-micro stage, and greatly improves the dynamic response of the system.

Lithography Macro-micro coupling model Mechanical resonance Hierarchical recognition Dynamic response

國家科技重大專項基金資助項目(編號：2009ZX02207)。

范文超(1990-)，男，現為哈爾濱工業大學控制科學與工程專業在讀碩士研究生；主要從事嵌入式系統設計和運動控制的研究。

TP273

A

10.16086/j.cnki.issn1000-0380.201505002

修改稿收到日期：2014-08-25。