履帶車輛轉向過程載荷的統計分析

李善樂， 王紅巖， 芮 強， 王欽龍， 郭 靜

(1. 裝甲兵工程學院機械工程系， 北京 100072； 2. 中國北方車輛研究所車輛傳動重點實驗室，北京 100072)

履帶車輛轉向過程載荷的統計分析

李善樂1， 王紅巖1， 芮 強1， 王欽龍1， 郭 靜2

(1. 裝甲兵工程學院機械工程系， 北京 100072； 2. 中國北方車輛研究所車輛傳動重點實驗室，北京 100072)

為研究履帶車輛在隨機環境下的行駛載荷，利用解析法和響應面相結合的方法,建立了履帶車輛轉向載荷替代模型，并采用蒙特卡洛抽樣方法,分析了統計情況下車速、摩擦因數和行駛阻力系數對驅動力矩和制動力矩的影響，最后通過實車試驗對計算結果進行了統計驗證。結果表明：計算結果與試驗結果統計分布一致，證實了所提方法的科學性，為履帶車輛在復雜隨機環境下行駛載荷的統計計算提供了新的途徑。

履帶車輛；統計特征；轉向運動；響應面模型

目前，國內外學者[1-2]對履帶車輛的研究大都是基于Wong[3]建立的履帶車輛穩態轉向模型，主要考慮履帶與地面之間在剪切作用下的滑轉、滑移、質心和幾何中心不重合以及高速時離心力條件下的轉向模型。上述研究工作中都引入了行駛阻力系數和摩擦因數等環境變量，求解時將這些地面環境參數作為確定量來考慮，計算結果只是某一特殊情況，不能全面反映履帶車輛的實際運行狀況。為了研究履帶車輛在隨機環境下的行駛載荷，筆者采用轉向載荷解析法和響應面相結合的方法構建隨機環境下轉向載荷替代模型，并進行了實車試驗驗證。

1 履帶車輛轉向過程分析與建模

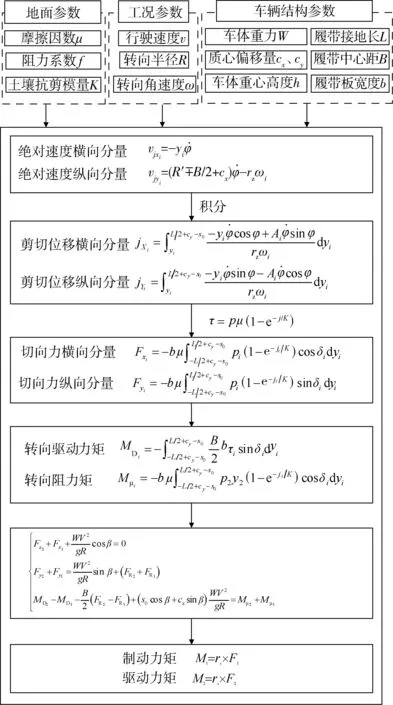
圖1 履帶車輛轉向模型框圖

圖2為車輛轉向模型的迭代求解流程，可以看出：履帶車輛轉向過程的求解是在給定車輛結構參數、行駛速度、轉向半徑的基礎上，對轉向極偏移量A1、A2、A3賦初值，然后代入圖1所示的模型方程中進行求解得到的。

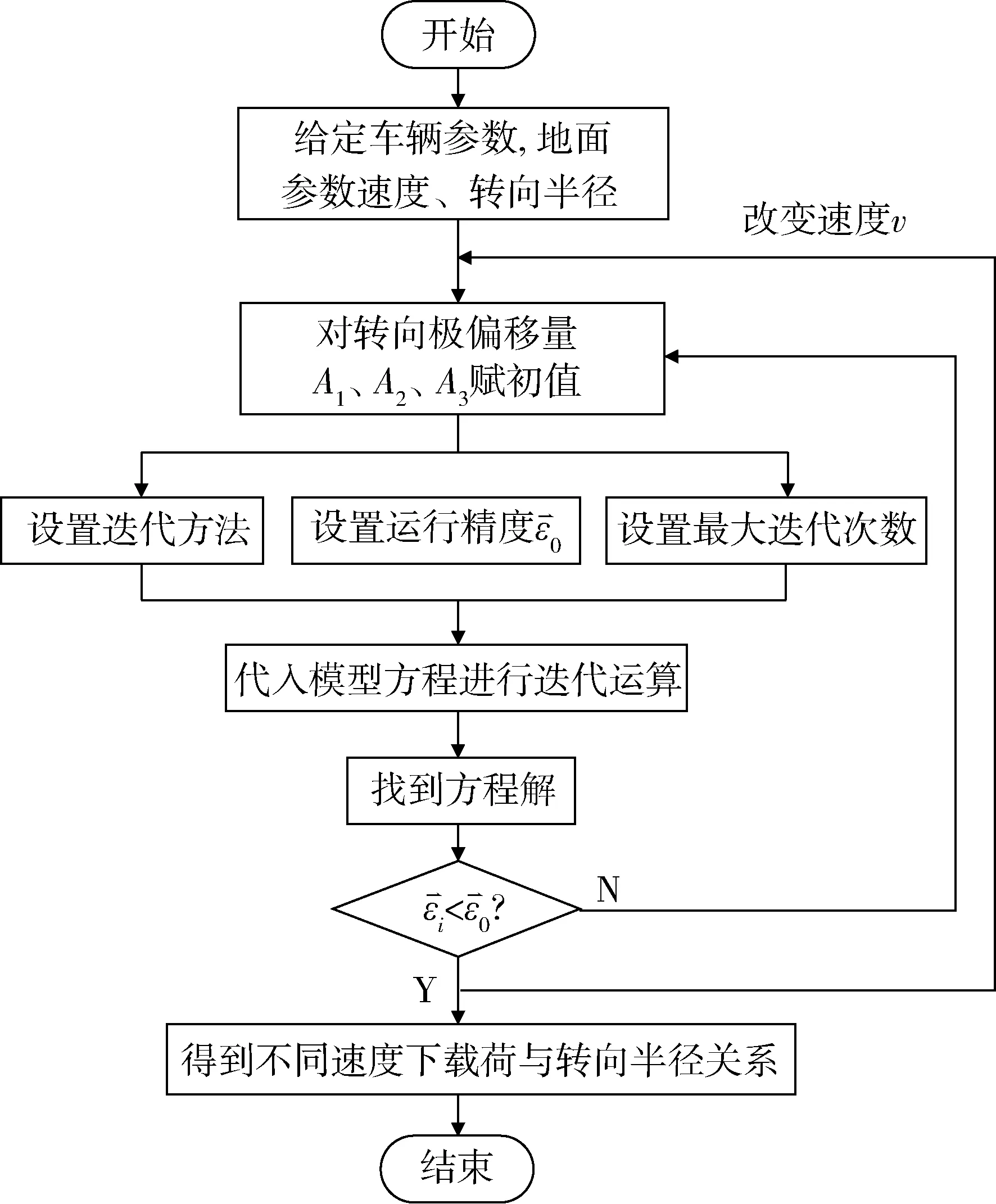
圖2 轉向模型解算流程

2 行駛地面和工況參數的統計模型

2.1 履帶車輛地面參數的統計

履帶車輛實際行駛的環境極其復雜，包括行駛阻力系數、摩擦因數等多種不確定性因素。大量的統計數據表明：這些隨機變量服從一定的分布規律[7]。根據計算模型的需要，給出幾種典型路面類型參數的統計特征值，如表1所示。

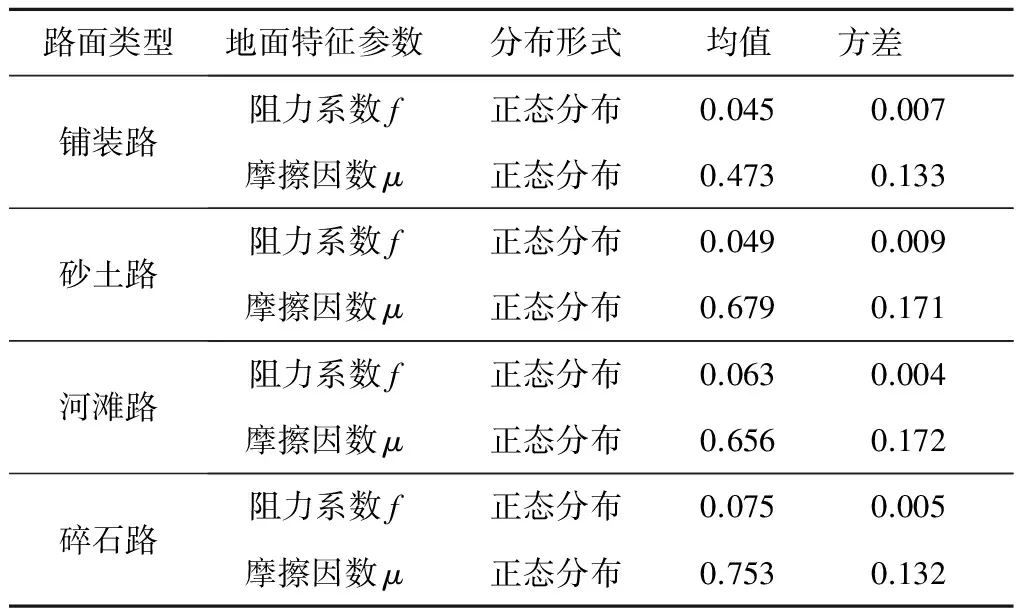
表1 不同路面類型特征參數

2.2 履帶車輛行駛工況統計

以某型履帶車輛在不同路面上進行的實車轉向試驗獲得的數據為基礎，通過對行駛速度進行統計，得到其速度分布的概率密度函數，如圖3所示，對應的概率密度函數特征參數如表2所示。

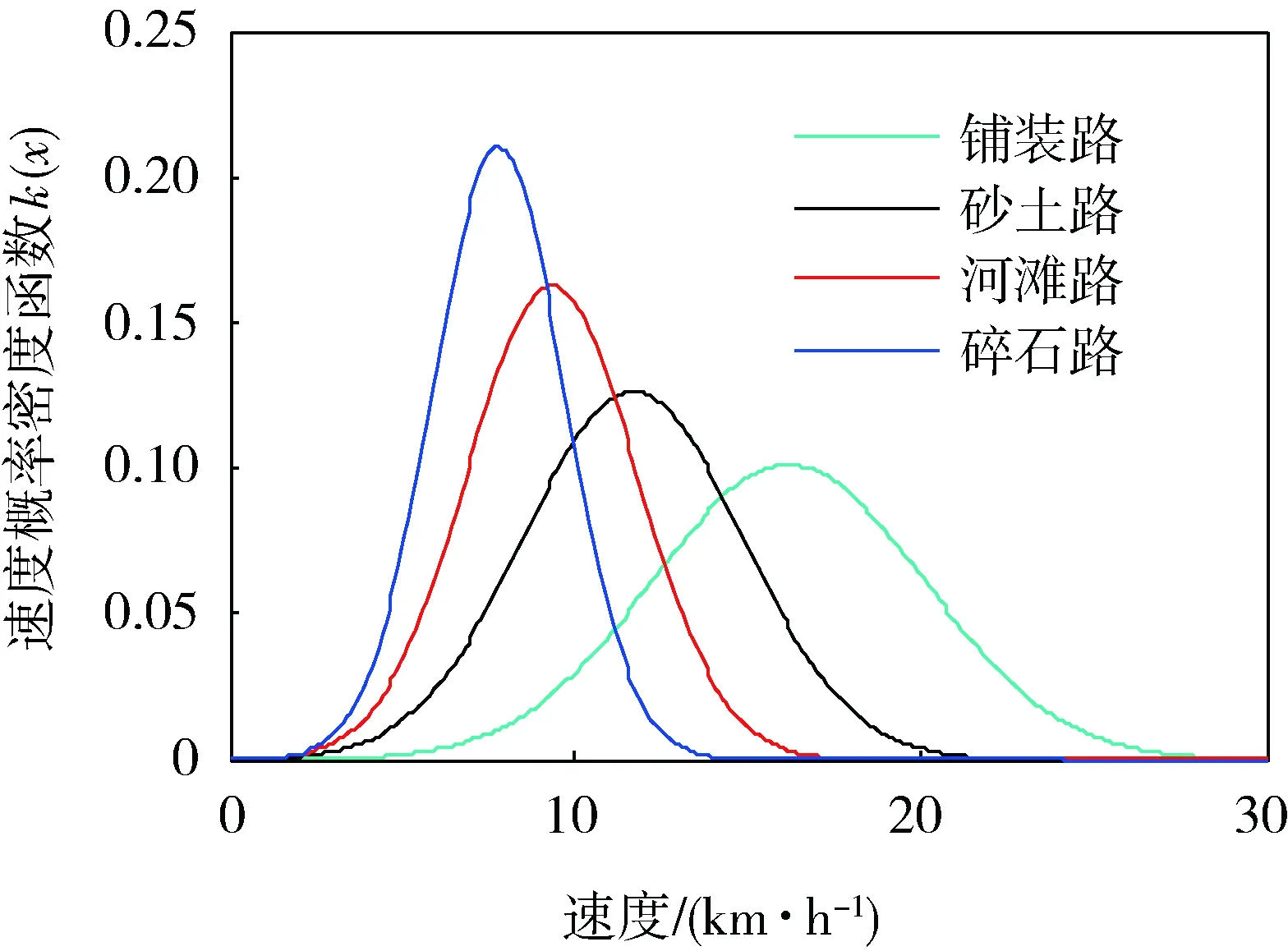
圖3 不同路面行駛速度的概率密度函數

表2 不同路面轉向行駛速度統計分布的特征參數

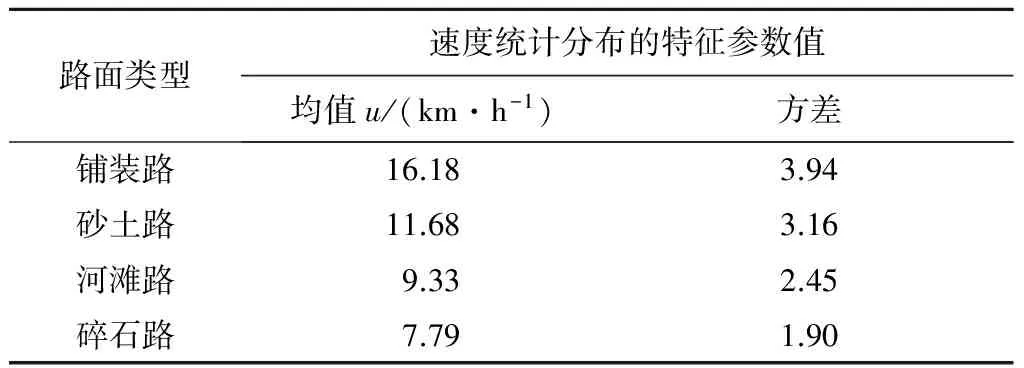
路面類型速度統計分布的特征參數值均值u/(km·h-1)方差鋪裝路16．183．94砂土路11．683．16河灘路9．332．45碎石路7．791．90

3 轉向載荷替代模型的建立及結果分析

3.1 轉向載荷替代模型的建立

履帶車輛運動過程中的載荷與行駛工況和地面環境有關。當轉向模型中的地面參數和工況參數為隨機變量時，若采用如圖1、2所示的解算過程，則存在規模大、計算周期長的問題。替代模型[8]是在不降低精度的情況下，采用少量樣本點構造的計算量小、精度高的近似模型。因此，本文利用該模型代替原有的復雜模型進行分析。

3.1.1 測試樣本點的設計

由于拉丁超立方[9]設計的樣本點均勻地分布在整個設計空間，且每個因子水平只使用一次，能夠使用較少的樣本點反映整個設計空間的響應特性，因此本文選擇拉丁超立方設計法。

在轉向載荷模型中，影響載荷的參數有很多，這里選擇對轉向載荷影響較大的行駛速度、行駛阻力系數和摩擦因數為設計變量。根據拉丁超立方設計法進行取樣，抽取30個樣本點，最終得到的樣本點分布如圖4所示。

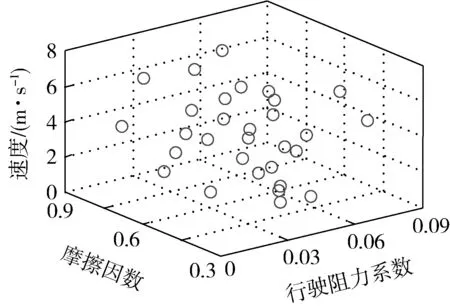
圖4 參數的樣本點分布

3.1.2 載荷替代模型的建立

以履帶車輛在砂土路轉向為例，用第1節中建立的轉向模型解析法對采樣的30個設計點進行計算，采用多項式響應面法建立替代模型，多項式響應面的一般形式為

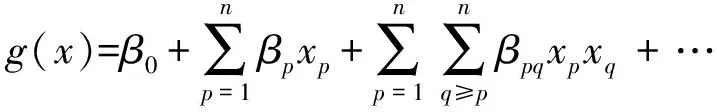
(1)

式中：xp、xq為自變量；n為自變量個數；β0、βp、βpq為待定系數。

根據實驗設計點的值及其響應，結合式(1)得到二階多項式響應面模型。圖5為f=0.05和μ=0.9時的響應面模型。通過檢驗可以得到：對于二階響應面替代模型，制動力矩的復相關系數為0.956，驅動力矩的復相關系數為0.976，復相關系數接近于1，表明多項式響應面替代模型精度滿足使用要求。

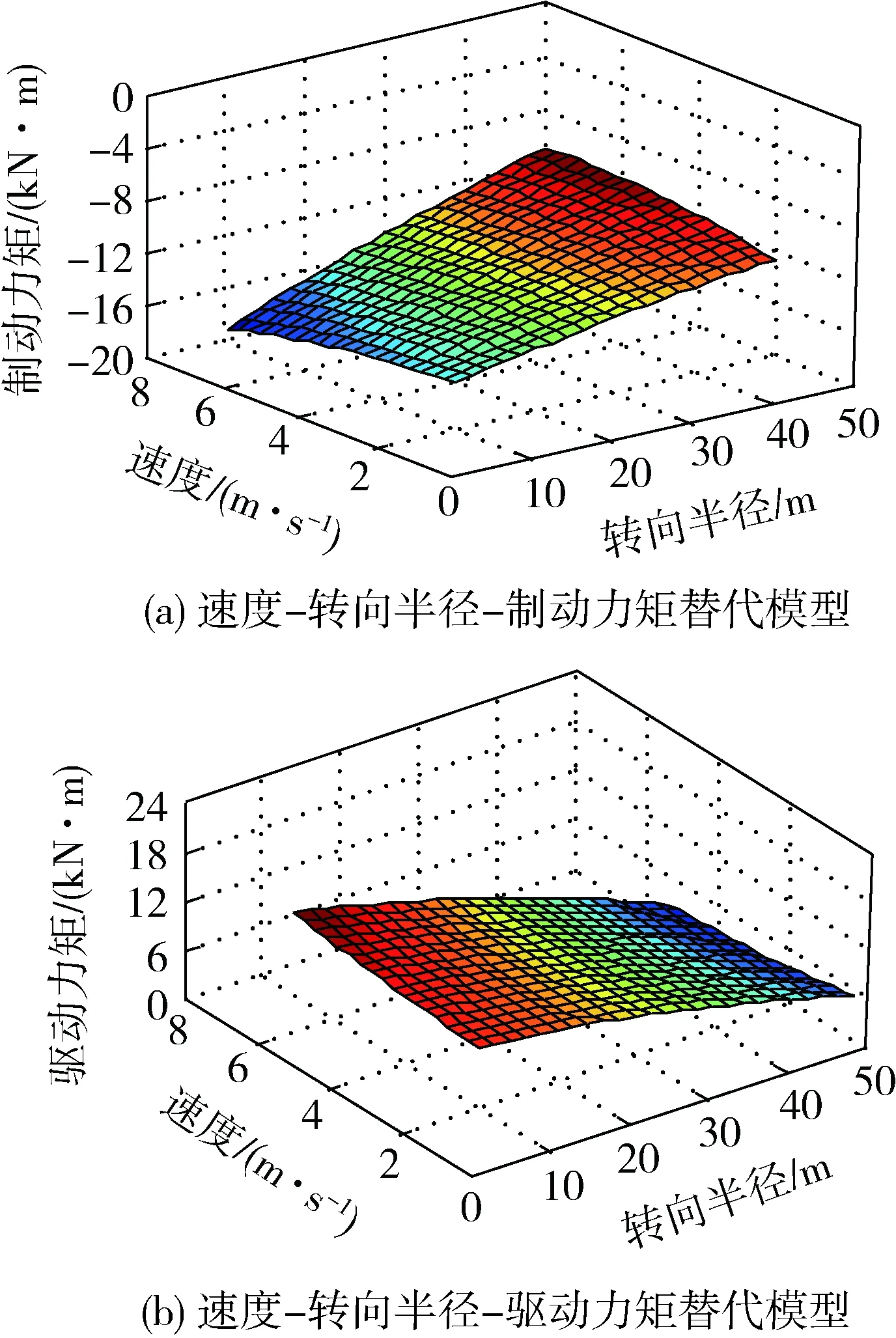
圖5 二階多項式響應面載荷替代模型

3.2 計算結果分析

3.2.1 轉向速度對載荷的影響

圖6(a)為f=0.05和μ=0.9時，速度按照正態分布進行1 000次蒙特卡洛抽樣計算得到的主動輪軸的驅動力矩、制動力矩與轉向半徑的關系曲線。可以看出：1)轉向力矩載荷隨著轉向半徑的增大而減小，這與常規的計算和試驗測試結果一致[1-2]；2)轉向速度對載荷的影響在一定的范圍內呈分散狀態，在半徑較小時，轉向速度使載荷分布的范圍變寬，隨著轉向半徑的增大，轉向速度對轉向載荷分布的影響減小。圖6(b)為相應的兩側主動輪軸驅動力矩、制動力矩分布的概率密度曲線，可以看出驅動力矩、制動力矩的離散程度以及概率密度分布情況，其不同顏色反映了概率密度的大小。

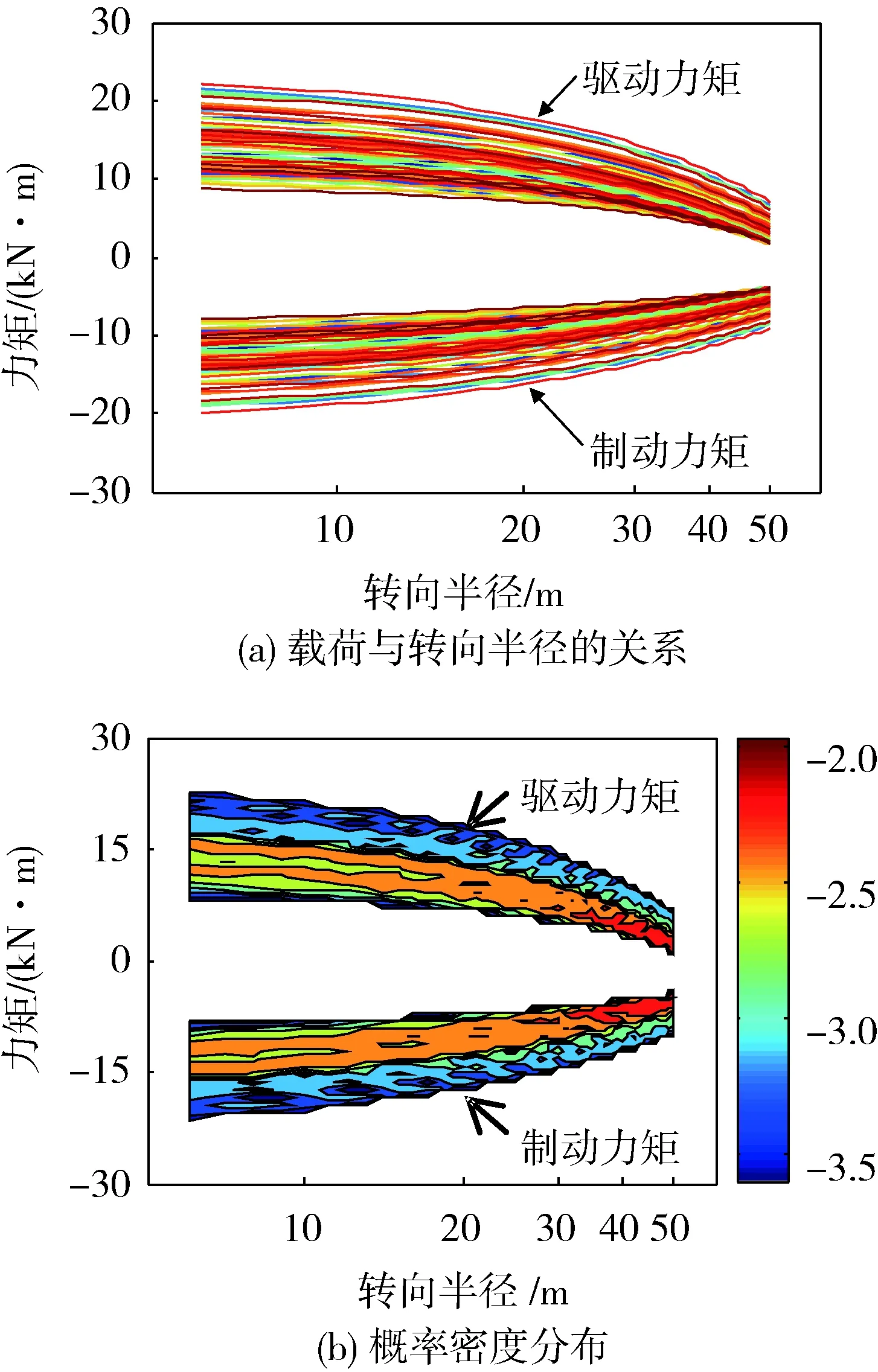
圖6 對速度抽樣得到的曲線分布

圖7為驅動力矩、制動力矩統計的直方圖以及根據直方圖擬合的分布，可以看出：驅動力矩、制動力矩很好地服從正態分布。

3.2.2 摩擦因數對載荷的影響

設摩擦因數服從正態分布，進行1 000次蒙特卡洛抽樣計算，f=0.05和v=2 m/s時的驅動力矩、制動力矩與轉向半徑的關系曲線如圖8(a)所示。可以看出：載荷在一定的范圍內呈分散狀態，在轉向半徑較小時，摩擦因數使載荷分布的范圍變寬；隨著轉向半徑的增大，摩擦因數對轉向載荷分布的影響程度降低。圖8(b)為相應的驅動力矩、制動力矩分布的概率密度曲線，可以看出：驅動力矩、制動力矩密度較大的區域基本分布在5～12 kN、-5～-12 kN附近，分別小于速度抽樣時分布的范圍。

圖7 力矩分布直方圖

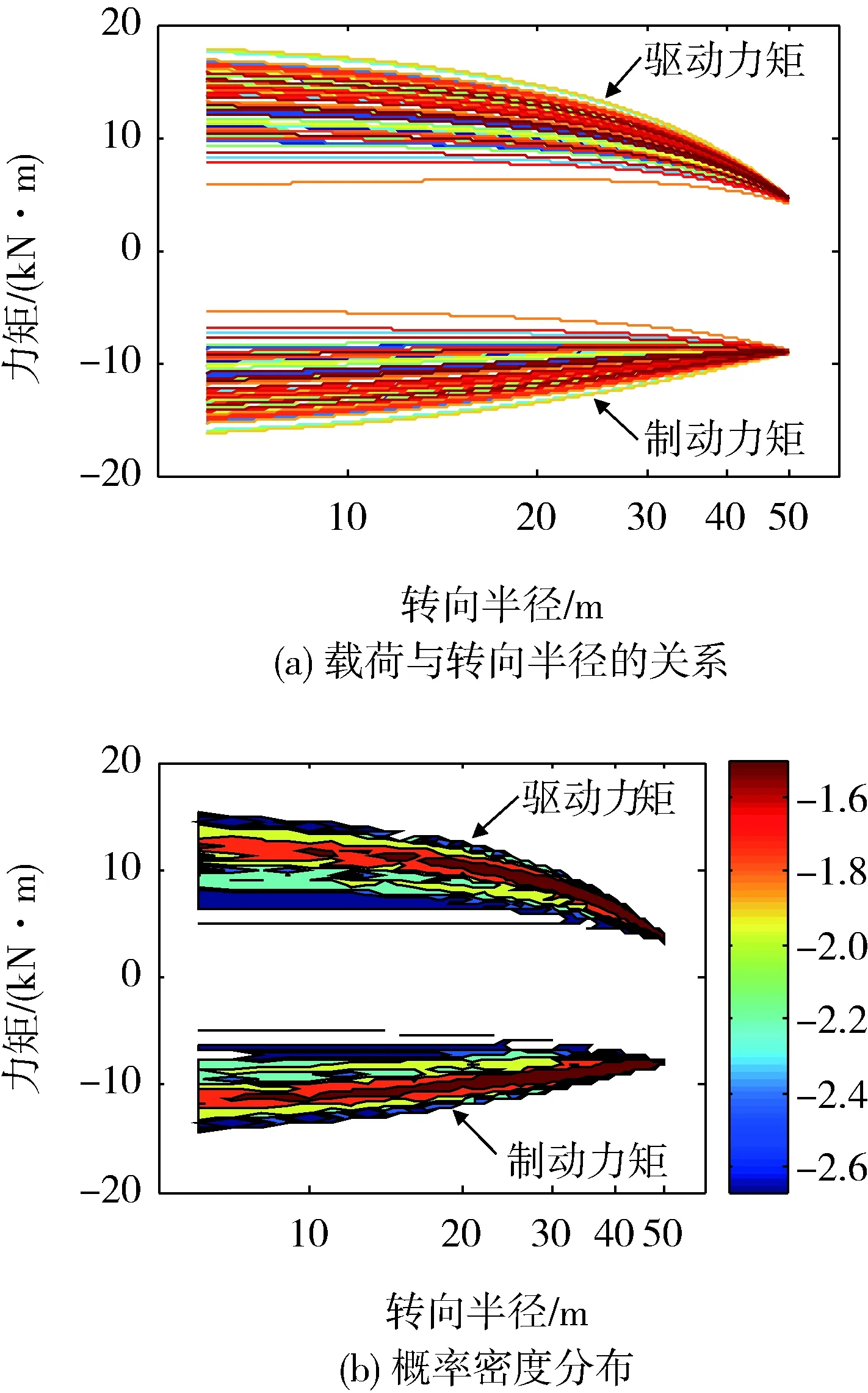
圖8 對摩擦因數抽樣得到的曲線分布

對比圖6(b)可以看出：1)對摩擦因數進行抽樣時，轉向載荷的較高概率密度范圍更廣，為10～50 m，這說明在整個轉向半徑范圍內，履帶與地面之間的摩擦因數對載荷都有較大的影響，這與實際情況相一致；2)當摩擦因數較小時，轉向載荷隨轉向半徑幾乎沒有變化，呈常量狀態，這基本屬于小概率事件。

3.2.3 行駛阻力系數對載荷的影響

對行駛阻力系數按照正態分布進行1 000次蒙特卡洛抽樣計算，其μ=0.9和轉向車速v=2 m/s時的驅動力矩、制動力矩與轉向半徑的關系曲線如圖9(a)所示，可以看出：載荷在一定的范圍內呈分散狀態，且行駛阻力系數在整個半徑范圍內對載荷的影響較為一致。圖9(b)為相應的驅動力矩、制動力矩分布的概率密度曲線，可以看出：1)力矩概率密度較大的區域基本分布在整個轉向半徑范圍內；2)在相同半徑下，載荷的分布變化范圍明顯小于對行駛速度和摩擦因數抽樣計算時得到的力矩的分布變化范圍。

圖9 對行駛阻力系數抽樣得到的曲線分布

從圖6-9可以看出：1)履帶車輛驅動力矩和制動力矩隨轉向半徑進行變化，轉向半徑增大時，履帶車輛的驅動力矩和制動力矩相應地減小；2)速度、摩擦因數和運動阻力系數統計分布會造成兩側力矩在較大范圍內變化，這是由環境和運行工況參數的不確定性引起的；3)轉向速度和摩擦因數對力矩的影響較大，而行駛阻力系數的影響較小，在以后的研究中可以不考慮行駛阻力系數對載荷的影響。

4 實車試驗及結果對比分析

4.1 履帶車輛轉向性能試驗

履帶車輛實車轉向性能試驗測試裝置如圖10所示，其中：NI測試系統能夠實現轉向過程中兩側主動輪轉速、車輛運行軌跡、行駛速度、航向角及綜合傳動裝置兩側輸出軸轉速、轉矩等數據的同步測試。

圖10 實車轉向性能試驗測試裝置

實車試驗過程中，被測試車輛在砂土路連續進行不同半徑的轉向，GPS記錄車輛轉向軌跡，轉速轉矩測試裝置記錄轉速和轉矩，數字羅盤記錄車輛的航向角，圖11(a)為GPS記錄的車輛行駛軌跡。由于測試車輛采用綜合傳動裝置，主動軸力矩測量困難，因此需先測量傳動系統輸出軸的扭矩，再轉化為驅動力矩、制動力矩，其傳動系統扭矩測試結果如圖11(b)所示。

4.2 試驗結果和計算結果對比分析

利用Matlab軟件對測得的試驗數據進行處理，其結果如圖12所示。為與理論計算結果對比，圖中給出了計算結果在95%置信區間內的邊界曲線，可以看出：1)當履帶車輛在不同的速度與轉向半徑下轉向時，由于實際環境參數和車輛運行工況的影響，驅動力矩、制動力矩在一定的范圍內分布，并隨著轉向半徑的增大而減小；2)試驗測得的驅動力矩與制動力矩基本分布在計算結果的95%置信區間內，說明計算結果和試驗結果具有很好的統計一致性。

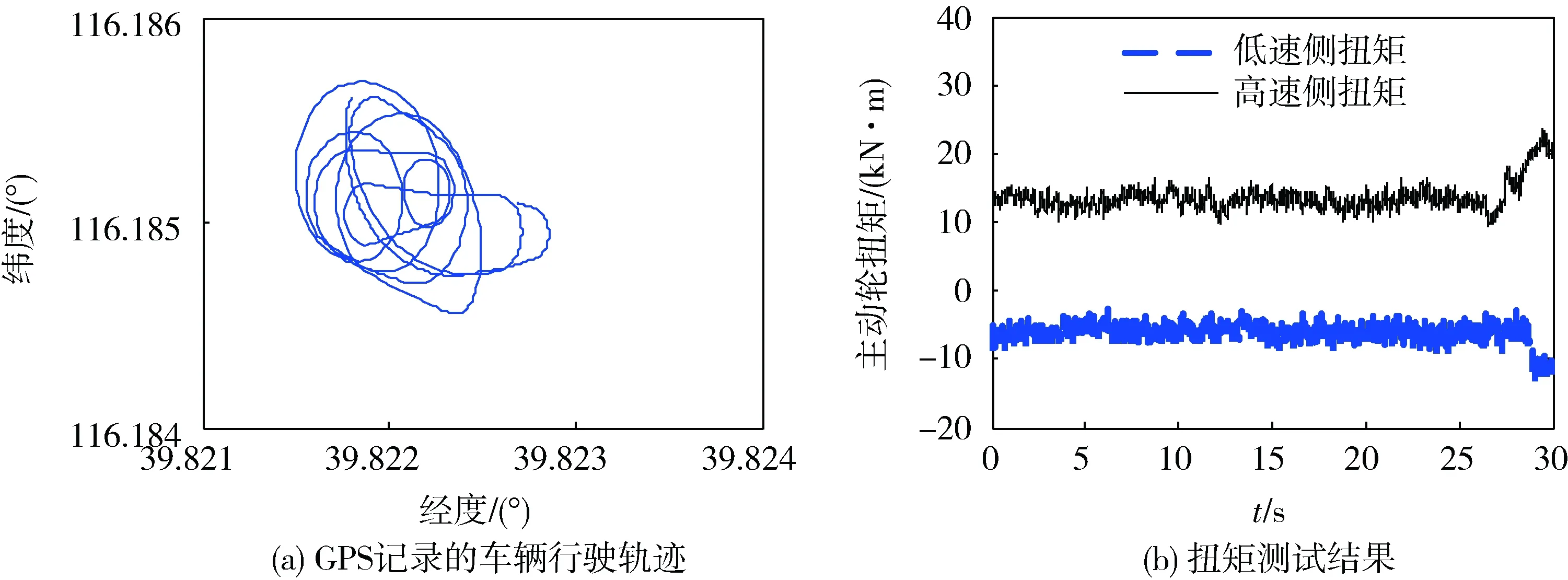
圖11 部分數據試驗測試結果

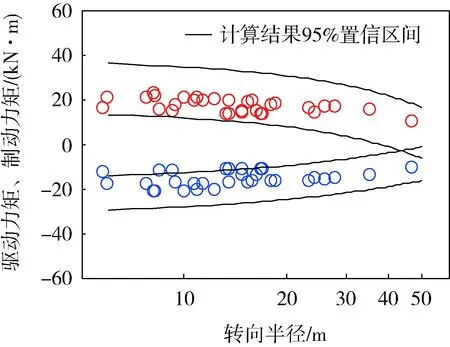
圖12 試驗測試結果與計算結果的對比

圖13為試驗測得的驅動力矩、制動力矩分布直方圖，可以看出：驅動力矩和制動力矩服從正態分布。表3為驅動力矩、制動力矩的統計規律以及與計算值的對比，可以看出：計算結果和試驗結果的統計規律具有較好的一致性，都服從正態分布，誤差較小，說明這種計算隨機載荷方法是正確的。

圖13 試驗測得的力矩分布直方圖

表3 計算結果與試驗結果統計規律對比分析

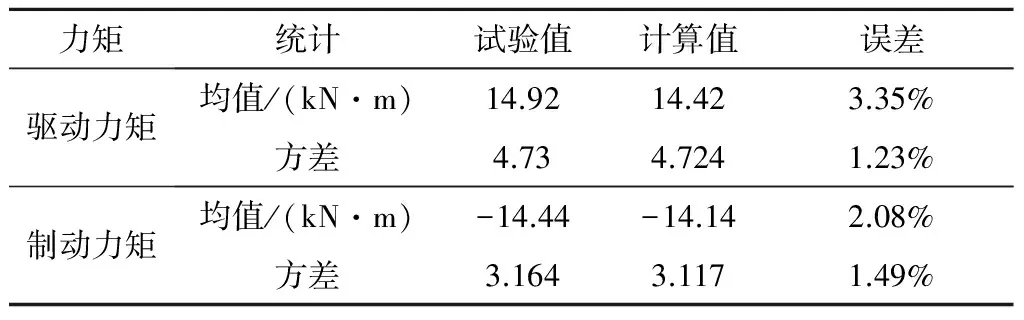
力矩統計試驗值計算值誤差驅動力矩均值/(kN·m)14．9214．423．35%方差4．734．7241．23%制動力矩均值/(kN·m)-14．44-14．142．08%方差3．1643．1171．49%

[1] Maclaurin B. Comparing the Steering Performance of Skid and Ackermann Steered Vehicles[J]. Automobile Engineering, 2008, 222(5):39-56.

[2] 王紅巖，王欽龍，芮強,等.考慮履帶滑動的轉向過程的仿真與試驗驗證[J].裝甲兵工程學院學報, 2014,28(2):31-35.

[3] Wong J. Theory of Ground Vehicles [M]. 3rd Edition. New York: John Wiley & Sons, 2001: 141-144.

[4] Said A M，Lakmal D S，Kaspar A. Track-terrain Modelling and Traversability Prediction for Tracked Vehicles on Soft Terrain[J]. Journal of Terramechanics，2010，47(3)：151-160.

[5] Wong J Y, Chiang C F. A General Theory for Skid Steering of Tracked Vehicles on Firm Ground[J].Journal of Automobile Engineering, 2001, 215(3): 343-355.

[6] 程軍偉，高連華，王紅巖,等. 履帶車輛轉向分析[J]. 兵工學報，2007，28(9)：1110-1115.

[7] 居乃鵕．裝甲車輛動力學分析與仿真[M]．北京：國防工業出版社，2002：16-35.

[8] 龍騰，劉莉，孟令濤，等．基于代理模型的翼型多目標集成優化設計[J].系統仿真學報, 2010, 22(7): 1604-1608.

[9] McKay M D，Conover W J，Beckman R J． A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code[J]. Technometrics, 1979, 21(2):239-245．

(責任編輯:尚菲菲)

Statistical Analysis on Loading of Tracked Vehicles in Steering Process

LI Shan-le1, WANG Hong-yan1, RUI Qiang1, WANG Qin-long1, GUO Jing2

(1. Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China; 2. Key Laboratory of Vehicle Transmission, China North Vehicle Research Institute, Beijing 100072, China)

To study the driving load of tracked vehicles in stochastic environment, a superseded model of steering loading is built by using response surface and analytic method. Based on this superseded model, effects of statistical vehicle velocity, friction coefficient and motion resistance coefficient on traction and braking torques by means of Monte Carlo are analyzed. A certain tracked vehicle is tested at last and testing results are statistically analyzed. The scientificity of the method are verified with the coincidence of the computing results and testing result, which puts forward a new way to calculate the driving loading in complex stochastic environment.

tracked vehicles; statistical characteristics; steering motion; response surface model

1672-1497(2015)04-0040-06

2015-06-02

軍隊科研計劃項目

李善樂(1991-)，男，碩士研究生。

TJ811

A

10.3969/j.issn.1672-1497.2015.04.009