單點金剛石車削輥筒表面V型螺旋槽表面形貌仿真與試驗研究

□ 戰蓉潔 □ 吳大鳴 □ 趙中里 □ 劉 穎

北京化工大學高分子材料加工裝備教育部工程研究中心 北京 100029

微結構功能表面的成形方法已成為很多學者的研究方向。由于金剛石刀具具有硬度高、耐磨性強、導熱能力好等優點，超精密車削加工中常采用該刀具。對于被金剛石刀具加工后所產生的微結構表面，國內外很多學者進行了研究。其中，李榮彬［1-6］教授團隊對超精密加工做了很多詳細的系統性研究：①提出了表面形貌模型的建立與表面粗糙度的預測；②基于運動學和切削理論，針對自由曲面元件從CAD數據轉化到加工仿真以及誤差補償一系列過程，對加工條件與切削策略進行優化；③在快速伺服刀架加工技術中建立仿真系統對切削微結構微棱鏡陣列的研究；④在單點金剛石刀具加工所獲得的納米級精度表面上，研究了在加工過程中受主軸轉速和材料特性等影響，使刀具與工件產生的相對振動會對加工后的表面造成一定程度的影響。趙清亮［7］教授建立了動態仿真模型，對正弦波結構的功能表面進行了預測與試驗，對微結構的功能表面加工有重要的指導意義。

1 表面形貌形成分析與車削系統建模

單點金剛石刀具車削材料表面時，表面形貌的形成，可以認為是刀具輪廓不斷地進給重復與車削系統穩定程度的一個疊加合成的過程［8］，這樣，即可以將影響表面形貌的因素分為非幾何因素影響與幾何因素影響兩大類。由于單點車削的特點，綜合幾何因素影響表面形貌可以發現，殘留高度成為了決定表面形貌的一個重要因素，并且殘留高度可以通過工藝參數進給量以及刀尖圓弧半徑進行計算表征，而非幾何因素，包括車削設備的穩定性、工件材料的表面缺陷、積屑瘤等因素的影響，很難通過簡單的計算求得在微結構的表面產生了多大的影響，因此，可以通過仿真來模擬表面形貌。

在影響表面形貌的非幾何因素中，車削系統的穩定性是決定表面形貌的一個重要因素。車削系統可以簡化為一個彈簧-質量-阻尼的機械系統［7］，由此可得到機械系統的物理模型，如圖1所示。由于加工過程中刀位點會經過一個極坐標系向直角坐標系的轉變，所以整個系統的輸入為車削系統主軸C軸的旋轉角度θ，輸出為刀架Z軸刀位點。由此可以得出車削系統的傳遞函數為：

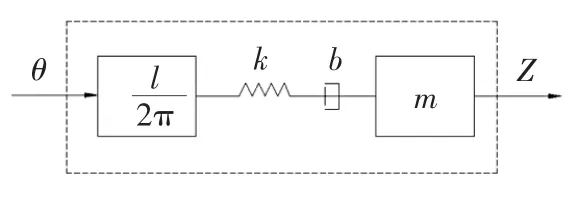
▲圖1 機械系統物理模型

式中：l為絲杠螺距；k為等效剛度系數；m為等效質量；b為等效阻尼系數。

2 模擬結果及分析

表面刻劃V型槽結構的輥筒模具，在光學領域由于其有復制連續及加工方便等優點，在工業化加工中得到了廣泛應用。而傳統的加工方法是在加工設備上，基于主軸的旋轉，在輥筒表面進行V槽刻劃，一個V槽結束后再進行第二個V槽的刻劃，在加工過程中，主軸的旋轉并沒有得到充分的利用，所以生產效率較低。對此，筆者提出了充分利用主軸旋轉的特點在輥筒表面刻劃V型螺旋槽的方法，用以提高加工效率。

在加工過程中，刀位點產生的刀具路線仍然為一個二維曲線，唯一不同的是在連續的螺旋槽加工過程中，刀位點為主軸轉速和進給量的函數，方程為：

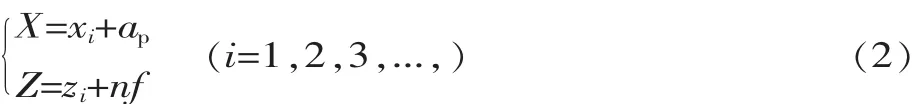
式中：zi為第i次切削時刀具初始z坐標值；xi為第i次切削時刀具初始x坐標值；n為主軸轉速；f為進給量；ap為切削深度。

刀觸點軌跡方程為：

式中：ri為第i次切削所產生的半徑值，ri=D/2-iap；D為未加工零件直徑；θ為主軸轉角，θ=wt=2πnt，w 為主軸角速度；t為時間。

刀觸點軌跡路線如圖2所示。

由于加工過程中刀觸點所走過的路線為一條螺旋線，在刻劃好的輥筒表面進行滾壓復制時，相對于傳統的加工方法會產生一定的誤差，而這種誤差在刻劃后的輥筒表面展開后，可以用傾斜的角度即螺紋升角α來進行測量，而α是螺距與螺紋中徑的函數：

式中：h為V型槽的深度；D2為螺旋線的中徑，且D2=D-0.609 5 h。

如果采用半徑為150 mm的輥筒進行刻劃，刻劃后微結構的螺紋升角為0.002 43°，可見，隨著輥筒半徑的增加，在滾壓復制時產生的誤差會減小。

▲圖2 刀觸點曲線

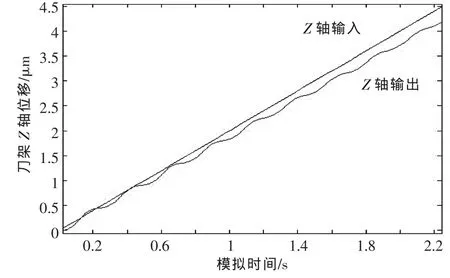
▲圖3 刀架Z軸輸入輸出曲線

基于以上理論，通過MATLAB/Simulink建模可以得到車削過程的控制系統，其輸入為計算后得到的理論刀位點，輸出為實際得到的刀位點。模擬仿真切削工件直徑為100 mm，工藝參數為：主軸轉速n=300 r/min，進給量 f=0.2 μm/s，切削深度 ap=10 μm，采用刀尖角為90°、刀尖圓弧半徑為1 μm的金剛石刀具進行加工。由于進行輥筒外緣車削，切削深度一定，所以刀架X軸沒有位移，僅刀架Z軸作直線移動，由此可以得到刀架Z軸的位移曲線，如圖3所示。可以看出，刀架Z軸的輸入為一條斜率一定的直線，而輸出由于加工系統的振動，會產生一定程度的波動，導致輸出并不是一條斜率一定的直線。

通過模型，由控制系統的輸入與輸出可以得到V型槽表面的理論曲線和實際加工得到的曲線，如圖4所示。由于系統的振動，使刀架Z軸產生了波動，最終在加工表面上產生了一定的波動，導致了加工出的表面并非是完美的V型槽結構，其理論曲線和實際加工曲線的誤差評價為：

式中:Zth為理論曲線值；Zre為實際曲線值。

在模擬結果中，選取誤差較大的點計算平均值后可以得到，T=7.1%，所以仿真系統所產生的誤差并不是很大。通過仿真得出V槽結構的曲面，選取5處距離較大的值作為表面粗糙度Ra的度量值，可以得到Ra的度量值 Ra=0.311 μm。

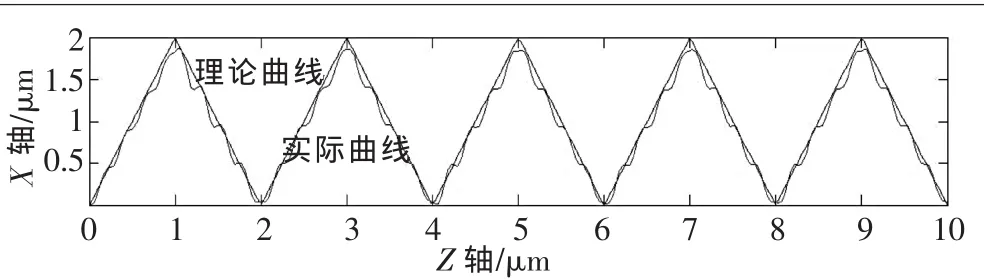
▲圖4 理論曲線與實際曲線

3 試驗檢測結果及分析

車削試驗在哈爾濱工業大學自行設計的超精密機床上進行，如圖5所示。所使用的金剛石刀具刀尖圓弧半徑為1 μm，刀尖角為90°，車削工藝參數、刀具參數以及V槽結構尺寸見表1。所加工的工件如圖6所示，材料為鋁6061，直徑150 mm，長度30 mm，在工件的外緣表面加工V型螺旋槽。

試驗后工件的表面形貌選用奧林巴斯OLS41003D測量激光顯微鏡進行檢測，如圖7所示。檢測時采用50倍的物鏡進行放大掃描，二維表面如圖8所示，三維表面立體圖如圖9所示。

▲圖5 車削系統

▲圖6 加工工件

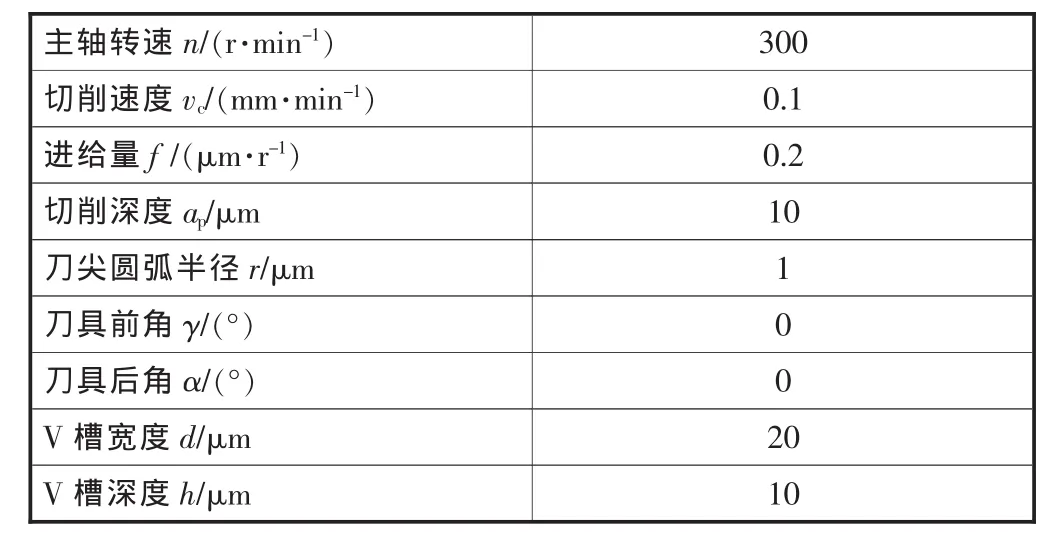
表1 車削工藝參數、刀具參數以及V槽結構尺寸

表2 測量表面粗糙度

在所得到的二維表面形貌圖中，截取9處進行粗糙度測量，測量結果見表2，其中1、2、3處為V槽頂角處的粗糙度值，4、5、6為 V 槽底角處的粗糙度值，7、8、9為V槽側面的粗糙度值。

對三組粗糙度測量結果求平均值后得到V槽頂角處、底角處和側面的粗糙度分別為0.127 μm、0.389 μm、0.031 μm。在 3處粗糙度中，V槽側面形貌是由所使用的刀具側面形貌所產生的，可以看出，切削中側面產生的振動并非最大，故側面的粗糙度由刀具的刃磨情況而定，通常會比較小。而V槽頂角處形貌是由兩次進給量之間的刀具切削后所剩形貌而產生，所以此處的粗糙度由加工設備以及工藝參數的精度而決定。V槽頂角形貌在切削過程中是刀尖接觸工件進行切削而產生的，此處所形成的表面粗糙度是由加工系統中所產生的振動而形成，選取此處與仿真計算所得的粗糙度值比較可知，結果相差并不是很大，進一步驗證了模型的可行性。

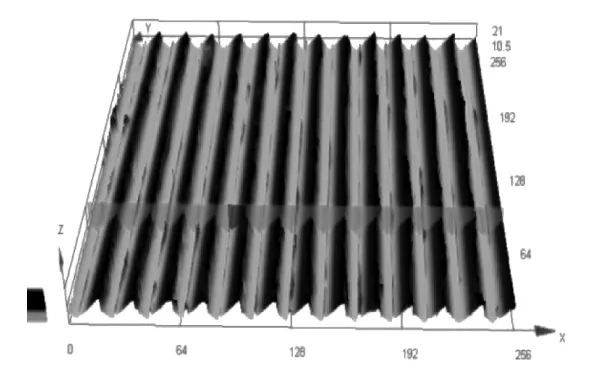
▲圖9 三維表面立體圖

▲圖7 3D測量激光顯微

▲圖8 二維表面形貌圖

4 結論

（1）提出了輥筒表面刻劃V型槽結構的高效方法，建立了刀位點軌跡方程與刀觸點軌跡方程，通過計算螺紋升角，驗證了該刻劃方法在進行復制滾壓時所產生的誤差為0.002 43°，證明了該方法的有效性。

（2）建立了車削加工系統模型，并通過設置輸入與輸出，仿真出刀架Z軸的實際位移以及V型槽的實際曲線，并對該模型仿真出的V型槽結構進行了誤差評價，證明了系統所產生的誤差不是很大。

（3）通過所提出的加工方法，選定工件進行試驗并進行檢測，得到了V槽底角的表面粗糙度Ra=0.389 μm，與仿真計算所得到的粗糙度值相差不大，驗證了車削系統模型的有效性，并進一步說明了加工方法的可行性。

［1］ 李榮彬，張志輝，李建廣.超精密加工的三維表面形貌預測［J］.中國機械工程，2000，11（8）：845-848.

［2］ Cheung C F，Lee W B.Modelling and Simulation of Surface Topography in Ultra Precision Diamond Turning ［J］.Journal of Engineering Manufacure，2000,214（6）：463-480.

［3］ 李榮彬，張志輝，杜雪，等.自由曲面光學元件的設計、加工及面形測量的集成制造技術 ［J］.機械工程學報，2010，46（11）：137-148.

［4］李榮彬，張志輝，杜雪,等.微結構光學元件快速伺服刀架加工技術研究［J］.納米技術與精密工程，2005，3（3）：216-221.

［5］ Cheung C F，Kwok T C，Li H F，et al.A Study of Factors Affecting Surface Quality in Fast Tool Servo Machining of Micro-lens Array ［C］.Proceedings of 2006 International Conference on Micro/Nano Fabrication Technologies（ICM/NFT’06），Bangkok，Thailand，2006.

［6］ 陳俊云，趙清亮，羅健.單點金剛石車削中刀具-工件相對振動的研究［J］.機械工程學報，2011，47（17）：135-140.

［7］ 趙清亮，王義龍，于光，等.微結構功能表面的金剛石超精密加工仿真與試驗［J］.機械工程學報，2009，45（12）：173-181.

［8］ 陳俊云，趙清亮.單點金剛石車削表面粗糙度研究［J］.北京工業大學學報，2012，38（7）：1013-1019.