螺旋推進車輛轉向動力學特性仿真分析
郭曉林, 劉 杰, 孫 偉, 趙 炎
(裝甲兵工程學院機械工程系,北京 100072)
螺旋推進車輛轉向動力學特性仿真分析
郭曉林, 劉 杰, 孫 偉, 趙 炎
(裝甲兵工程學院機械工程系,北京 100072)
為了探究螺旋推進車輛在低速條件下的轉向動力學特性,建立了螺旋推進車輛轉向動力學模型,采用數值軟件結合牛頓迭代法對動力學模型進行了仿真,研究了整車轉向過程中縱向力及轉向力矩的變化規律。結果表明:隨著相對轉向半徑增大,車輛內側制動力、外側牽引力、整車轉向阻力矩及轉向主動力矩均會減小。研究結果為螺旋推進車輛的設計與應用提供了理論依據,對工程實踐具有一定的指導意義。
螺旋推進車輛;轉向性能;運動學;動力學;仿真
由于螺旋推進車輛在濕軟地面上具有良好的通過性,因此自面世以來便引起了國內外學者廣泛的關注。1965年,Knight等[1]基于克萊斯勒公司生產的MSA(Marsh Screw Amphibian)車進行了多項性能測試,測試結果證明了在極端松軟條件下螺旋推進車通過性能強于履帶車;1967年,英國學者Dugoff等[2]通過MSA模型車實驗,研究了車輛結構、負載、土壤等因素對車輛行駛特性的影響;1998年,我國學者樊啟洲等[3]建立了軟黏土條件下的螺旋滾筒推進力模型,并給出了推進力的數學表達式;2010年,日本學者Nagaoka等[4]研究了月壤條件下螺旋推進模型車的推進力特性,并建立了推進力模型,得出了在一定范圍內螺旋滾筒推進力隨滑轉率單調遞增的變化規律。
目前,關于螺旋推進車的研究主要關注直駛過程中螺旋推進車結構參數和地面條件對其動力學特性的影響,忽略了整車轉向過程中的動力學表現[5]。然而車輛的轉向特性對評估車輛機動性具有特殊意義,轉向分析將為優化整車結構設計提供重要依據。本文借鑒履帶車輛轉向的研究方法,對螺旋推進車低速條件下的轉向動力學特性進行仿真分析,探討轉向動力學參數的變化規律。
1 整車轉向運動學分析
假設[6]:
1) 車輛重心位于幾何中心處,且沿中心縱軸對稱;
2) 車輛轉向過程發生在水平地段,屬于低速、穩定和常規轉向,不考慮過渡過程和離心力的影響;
3) 車輛轉向過程中行駛阻力系數不變;
4) 螺旋滾筒接地壓力沿縱向均勻分布,且不考慮其接地寬度的影響。
螺旋推進車在轉向過程中,螺旋滾筒做復合運動。復合運動包括牽連運動和相對運動,其中:在牽連運動中,螺旋滾筒繞轉向中心做旋轉運動;在相對運動中,螺旋滾筒繞自身轉軸線轉動。對于相對運動,如果螺旋滾筒轉速一定,則相對速度一定;對于牽連運動,螺旋滾筒上不同點的牽連速度各不相同,離轉向中心越遠,其牽連速度越大。
不同于常規車輛,螺旋滾筒的相對運動速度方向始終與滾筒接地中心線正交,這種特殊的運動方式使螺旋滾筒在實際轉向時,先有橫向的滑轉、滑移,而后產生縱向的滑轉、滑移,分析起來較為復雜。為了簡化分析過程,本文借鑒履帶車輛轉向的研究方法對螺旋推進車輛的轉向運動學特性進行分析。根據螺旋運動特性,螺旋滾筒繞自身轉軸的轉動提供前進的速度,忽略螺旋滾筒結構上的差異,將此速度看作行走機構的縱向相對速度,則整車轉向運動平面如圖1所示。
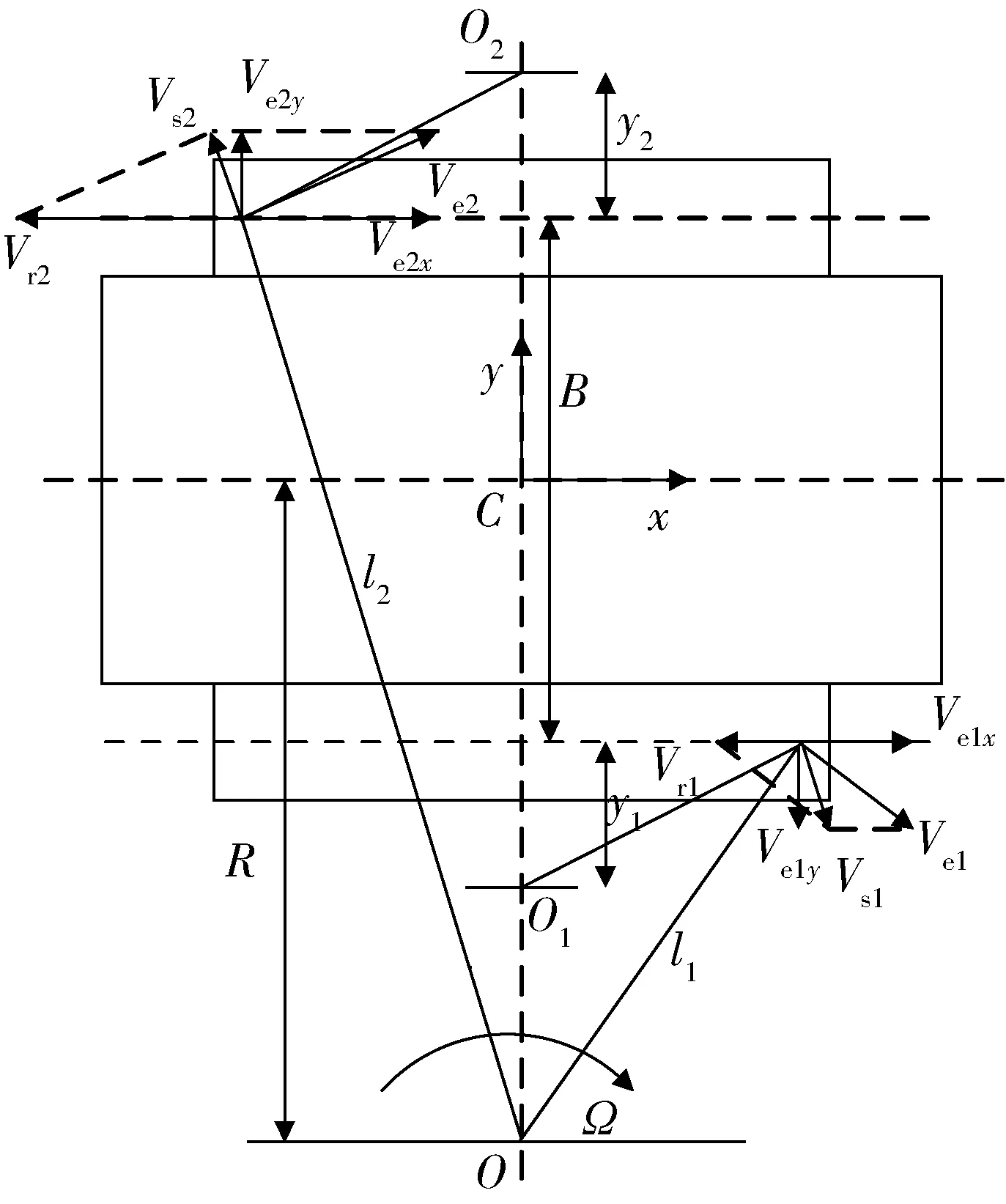
圖1 螺旋推進車轉向運動平面
圖1中:假設車輛沿x軸正向行駛,向右轉彎,車輛重心位于幾何中心C處;O為瞬時轉向中心;R為轉向半徑;Ω為轉向角速度;B為滾筒縱軸線之間的距離。為方便分析,設i=1,2,分別代表車輛內、外側,則有:Oi為滾筒轉向極;ωi為滾筒轉動角速度;Vei為滾筒上接地點的牽連速度;Vri為滾筒上該點的相對速度;Vsi為滾筒上該點的絕對速度;li為滾筒上該點到O點的距離;yi為內、外側轉向中心的橫向偏移量。
由差速轉向原理可知:直線行駛時ω1=ω2;向右轉向時ω2>ω1。
根據螺旋滾筒的運動特性,滾筒轉動時提供的理論前進速度為
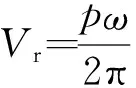
(1)
式中:p為螺旋滾筒的螺距;ω為螺旋滾筒的轉動角速度。
以低速大半徑轉向工況為例,根據圖1中關系可求得Vri、Vei和Vsi分別為
(2)
由式(2)可得:
(3)
式中:k=ω1/ω2,為內、外側螺旋滾筒的轉速之比;Δω=ω2-ω1,為外、內側滾筒的轉速差。
轉向過程中,內側滾筒始終處于制動狀態,發生滑移現象;外側滾筒始終處于驅動狀態,發生滑轉現象。內側滾筒的滑移率s1和外側滾筒的滑轉率s2分別為[7]
(4)
2 整車轉向動力學分析
螺旋推進車在轉向過程中主要受到牽引力和制動力的作用,且力矩包括轉向阻力矩和轉向主動力矩[8]。
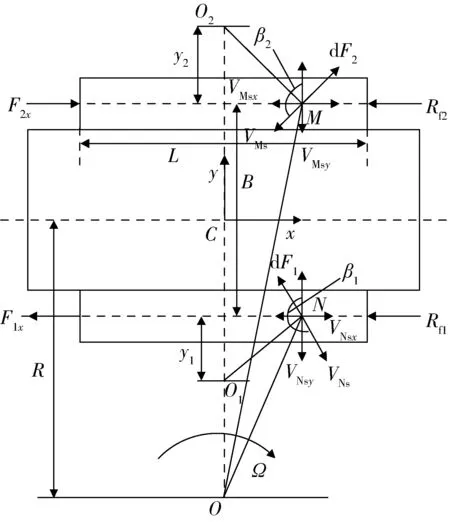
圖2 螺旋推進車轉向動力學示意圖
2.1 牽引力和制動力
圖2為螺旋推進車轉向動力學示意圖。在外側滾筒上任取一點M,假設地面作用于M點處微分段的切向反作用力dF2與單位長度上的正壓力成正比[9],轉向阻力系數為μ,則沿螺旋滾筒縱向接地中心線的分力為
dF2x=dF2sin(π+β2)=qμsin(π+β2)dx。
(5)
式中:
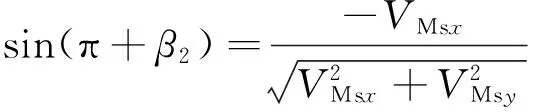
其中β2為M點絕對速度與y方向的夾角,VMsx、VMsy分別為M點絕對速度在x、y方向上的分量;q=G/(2L),G為車輛載重。
作用于外側滾筒上的牽引力F2x為接地段中心線上的微元力的積分,即

(6)
同理可得內側制動力為
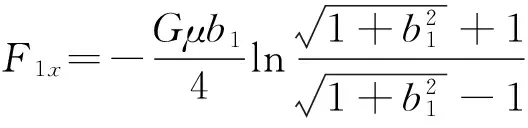
(7)
式中:b1、b2分別為內、外側轉向極的相對橫向偏移量,且b1=y1/(L/2),b2=y2/(L/2)。
根據F1x和F2x,可以計算內、外側滾筒轉向所需的制動力矩M1和驅動力矩M2為
(8)
2.2 轉向阻力矩和轉向主動力矩
2.2.1 特向阻力矩
仍以M點為例,取外側滾筒進行分析。由圖2可知:在M點處的土壤切向反作用力與該點絕對速度方向相反,則沿y軸方向的分力為
dF2y=qμcos(π+β2)dy。
(9)
式中:
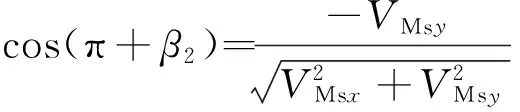
將此分力對螺旋滾筒接地段的幾何中心取矩,忽略接地寬度的影響,對整個接地段進行積分,可得到外側滾筒的阻力矩為
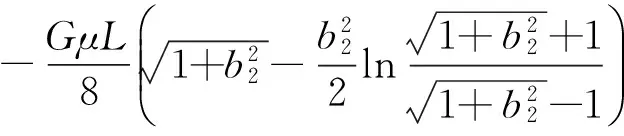
(10)
同理,內側滾筒的轉向阻力矩為
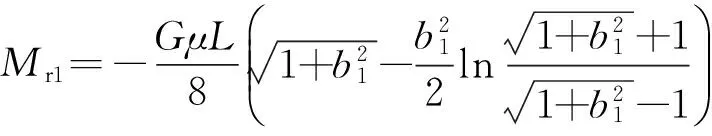
(11)
內、外側轉向阻力矩之和為
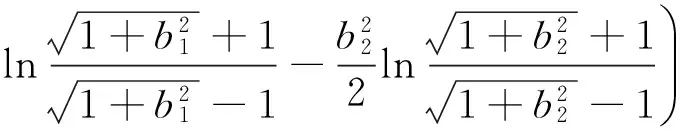
(12)
式中:負號表示阻力矩方向為逆時針方向。
2.2.2 轉向主動力矩
將內、外側滾筒的縱向力對幾何中心C點取矩,可得外側滾筒的主動力矩為
(13)
同理,內側滾筒的主動力矩為
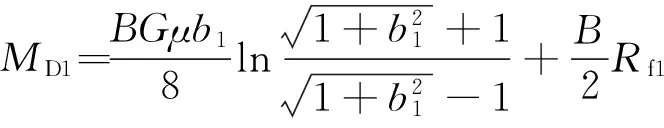
(14)
內、外側滾筒的主動力矩之和為
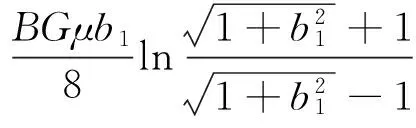
(15)
式中:Rf1、Rf2分別為內、外側滾筒受到的滾動阻力,且Rf1=Rf2。
3 整車轉向動力學模型
根據力平衡關系和力矩平衡關系,可得到螺旋推進車輛轉向的平面運動方程組為
(16)
即
(17)
將各個力和力矩代入式(17),可得:
(18)
式中:λ=L/B;

其中μ取值因無實驗數據作參考,參照履帶車輛轉向阻力系數表達式,令μmax=0.8;

為相對轉向半徑。
式(18)為超越方程,需采用數值解法求解。
4 模型仿真及分析
采用數值軟件結合牛頓迭代法進行數值模擬仿真,求解轉向模型中的非線性方程組。模型以克萊斯勒公司1965年生產的MSA螺旋沼澤車為研究對象[10],以灘涂地為主要作業環境,主要結構參數和地面條件參數分別如表1、2所示。
根據動力學模型,重點對以下變量之間的變化規律進行了仿真。
1) 整車內、外側縱向力F1x、F2x與ρ的關系
圖3為轉向過程中內、外側滾筒受到的制動力、

表1 MSA結構參數

表2 灘涂地面參數
牽引力隨ρ變化的曲線,可見:(1)當ρ較小時,制動力和牽引力均較大;(2)隨著ρ的增大,外側滾筒的牽引力和內側滾筒的制動力均逐漸減小;(3)當ρ增大到某一值時,內側滾筒受到制動力將減小為0,此時,車輛只有外側滾筒提供動力,將會發生分離轉向;(4)當ρ→∞時,車輛處于直線行駛狀態,兩側滾筒均受到牽引力的作用。
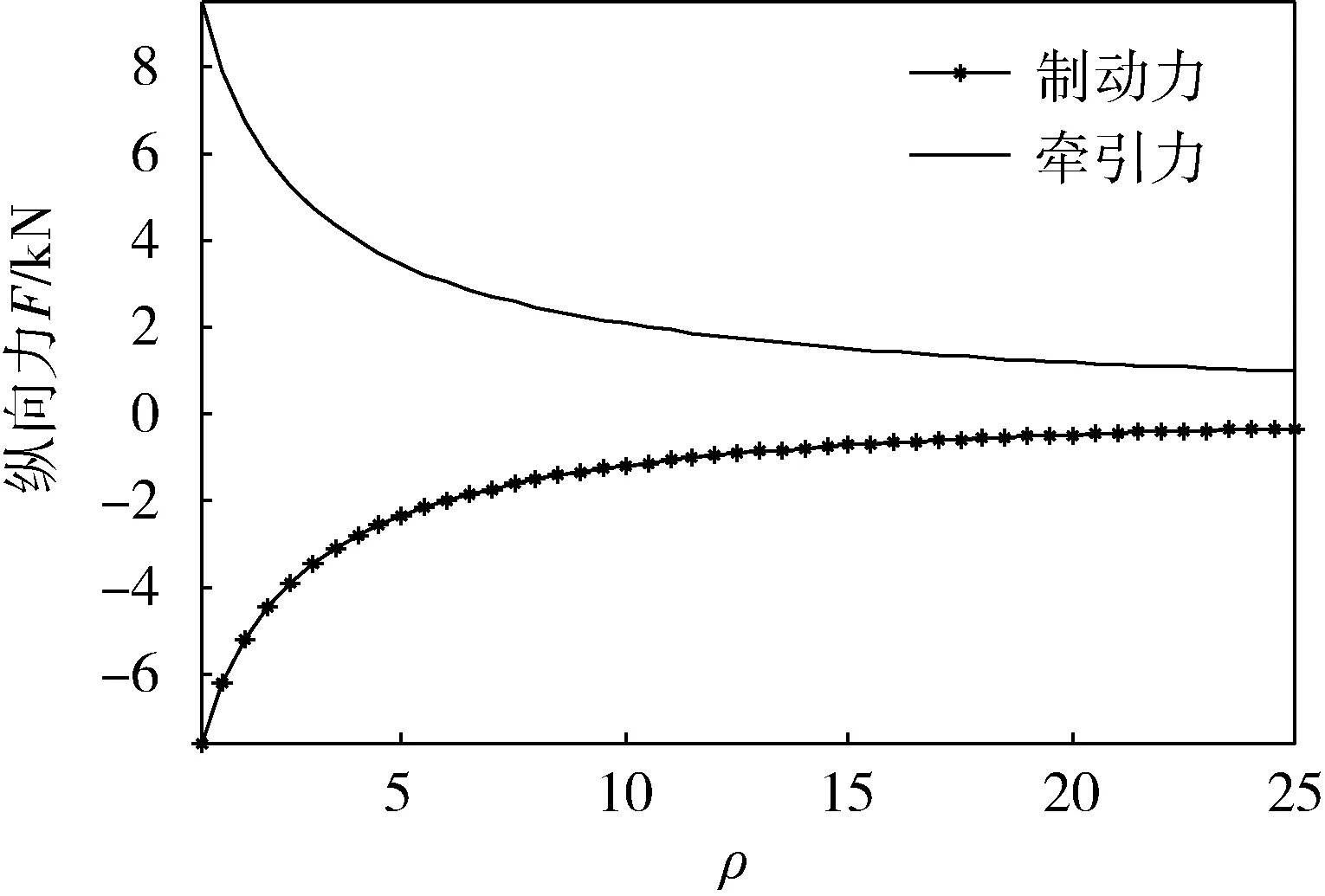
圖3 制動力、牽引力隨ρ變化曲線
2)整車轉向力矩與ρ的關系
圖4為轉向過程中車輛受到的轉向阻力矩和轉向主動力矩隨ρ變化的曲線。可見:(1)在轉向過程中,轉向主動力矩始終大于轉向阻力矩;(2)隨著ρ的增大,整車的轉向阻力矩和轉向主動力矩均減小;(3)當ρ增大到某一值時,轉向阻力矩趨近于0,車輛趨近于直線行駛狀態;(4)當ρ→∞時,車輛處于直線行駛狀態,此時轉向主動力矩為內、外側滾筒驅動力矩之和。
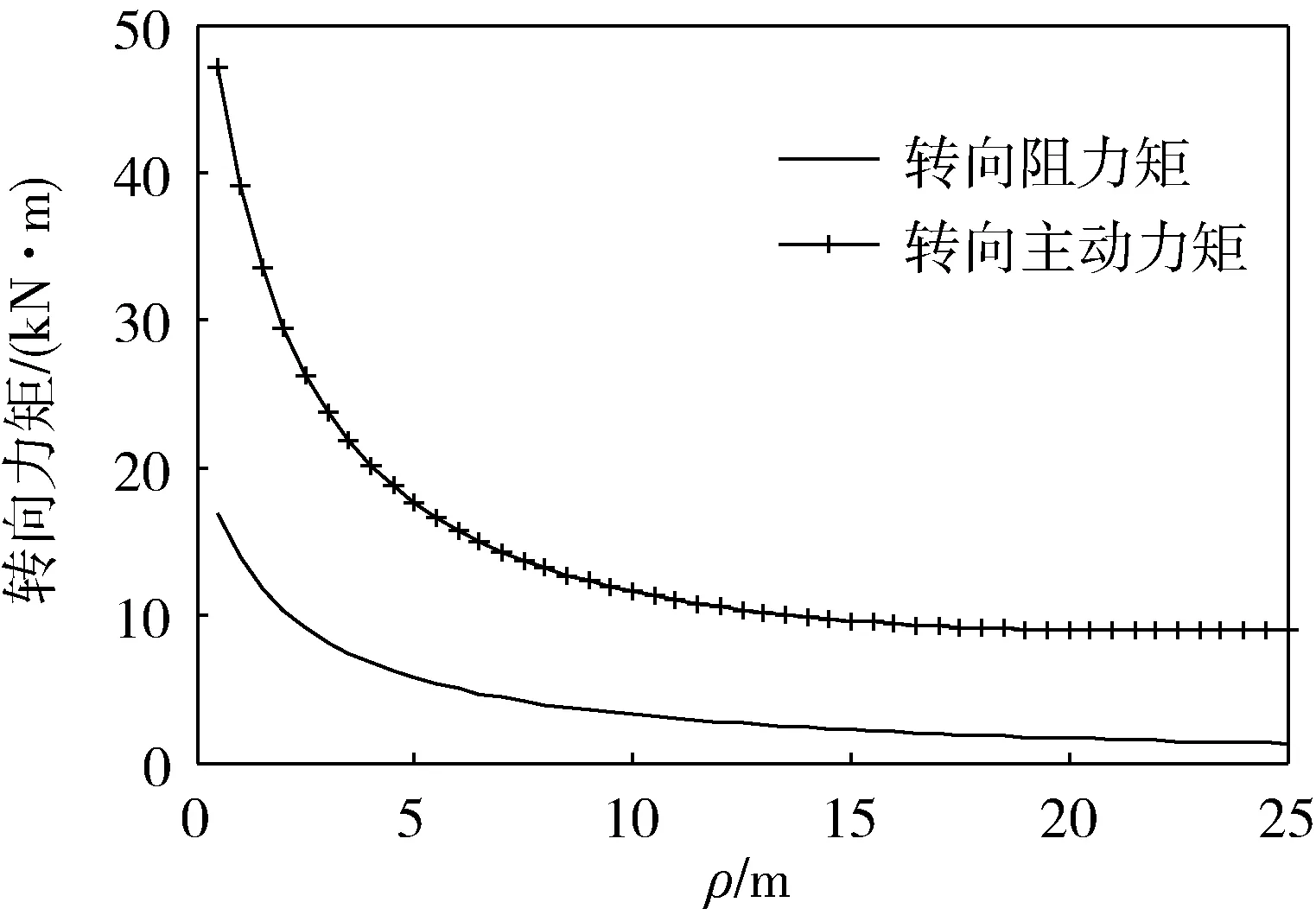
圖4 轉向力矩隨ρ變化曲線
3)滑動率si與ρ的關系
螺旋推進車輛在轉向過程中,內側滾筒由于受到制動力的作用而發生滑移現象,外側滾筒由于受到牽引力的作用而發生滑轉現象。圖5、6分別為轉向過程中滑轉率、滑轉率隨ρ變化的曲線,可見:(1)在ρ較小時,滑移率、滑轉率均較大,此時滑移、滑轉現象明顯;(2)隨著ρ的增大,滑移率、滑轉率均會減小至較小值,此時滑動現象不明顯。
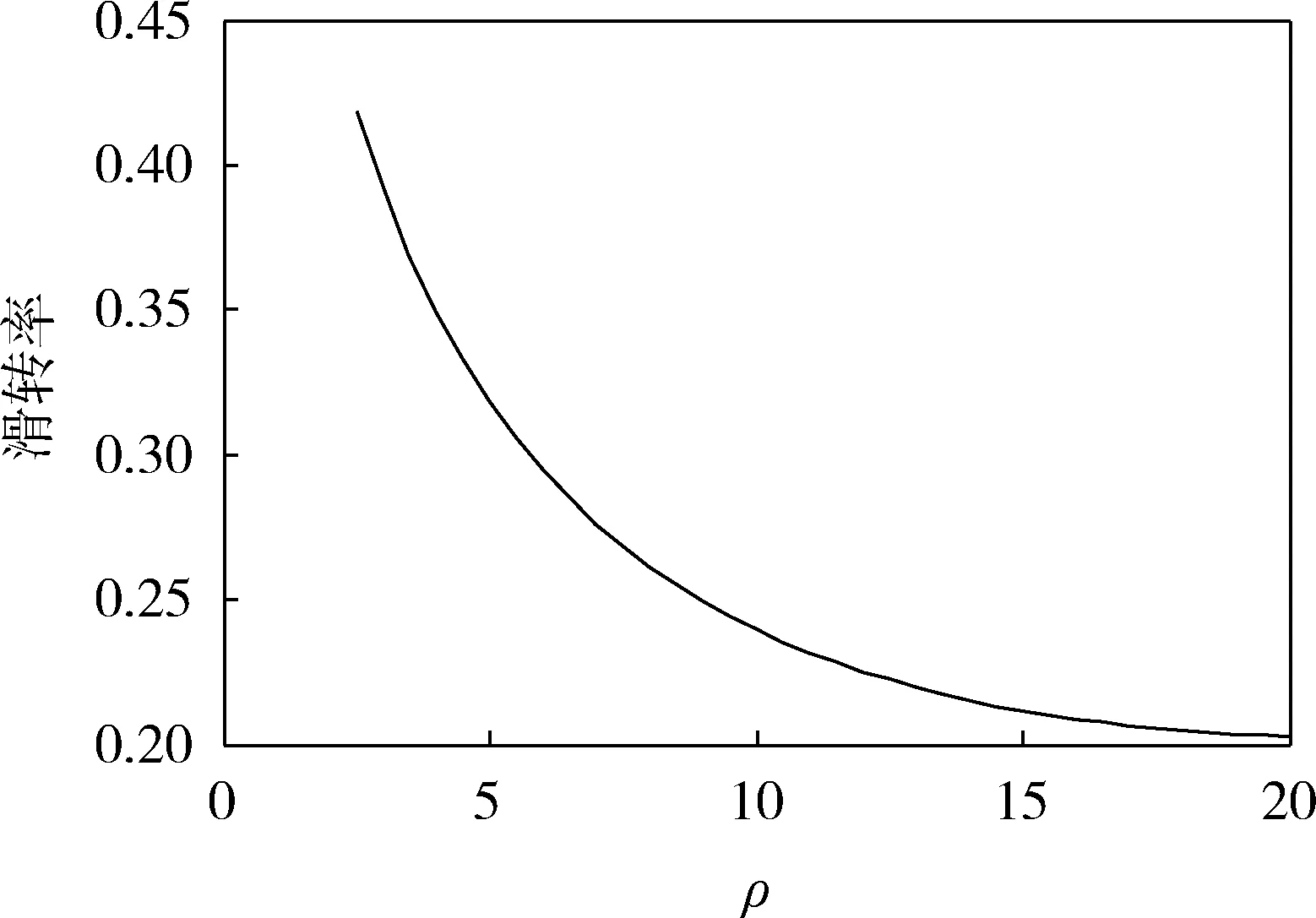
圖5 滑轉率隨ρ變化曲線

圖6 滑移率隨ρ變化曲線
5 結論
本文以螺旋推進車輛轉向過程中的動力學參數變化規律為研究對象,對車輛轉向過程中的動力學特性進行了仿真分析,為探究螺旋推進車輛轉向機理提供了依據。與以往不考慮車輛轉向過程中滑動現象的研究不同,本文綜合考慮了內、外側滾筒在轉向過程中的滑移、滑轉問題,確保了仿真分析的合理性。然而,螺旋推進車輛轉向過程中受力復雜,轉向動力學特性還與地面條件的相互作用有關,文中未能充分考慮。下一步,還需對車輛結構參數、地面條件對轉向特性的影響進行深入研究。
[1] Knight S J,Rush E S,Stinson B G.Trafficability Tests with the Marsh Screw Amphibian[J].Journal of Terramechanics,1965,2(4):31-50.
[2] Dugoff H,Ehrlich R.Model Tests of Buoyant Screw Rotor Cofigurations[J].Journal of Terramechanics,1965,4(2):9-22.
[3] 樊啟洲,邵耀堅.螺旋滾筒在粘土上推進力的研究[J].拖拉機與農業運輸車,1998(4):20-24.
[4] Nagaoka K,Otsuki M,Kubota T,et al.Terramechanic-based Propulsive Characterisics of Mobile Robot Driven by Archimedenam Screw Mechanism on Soft Soil[C]∥Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems.Taipel,Taiwan:IEEE,2010:18-22.
[5] 郭曉林,劉杰,趙炎,等.螺旋推進車研究現狀概述[J].農業裝備與車輛工程,2014,52(4):14-17.
[6] 宋海軍,高連華,程軍偉.履帶車輛中心轉向模型研究[J].裝甲兵工程學院學報,2007,21(2):55-58.
[7] 潘家平.輪式車輛穩態滑移轉向特性研究[D].北京:裝甲兵工程學院,2012.
[8] 王良曦,王紅巖.車輛動力學[M].北京:國防工業出版社,2008:111-120.
[9] 程軍偉,高連華,王紅巖,等.履帶車輛轉向分析[J].兵工學報,2007,28(9):1110-1115.
[10] Nbumeybr M J, Jones B D. The Marsh Screw Amphibian[J].Journal of Terramechanics,1965,4(2):83-88.
(責任編輯:尚菲菲)
Analysis of Simulation on Steering Dynamics Performance of Screw-driven Vehicle
GUO Xiao-lin, LIU Jie, SUN Wei, ZHAO Yan
(Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China)
In order to explore the steering dynamics characteristics of screw-driven vehicle in the condition of low-speed, the dynamics steering model of screw-driven vehicle is established. The dynamics model is simulated by Newton iteration method combining with numerical software to study the changing rule of the longitudinal forces and torque in the steering process. The results show that the lateral traction, medial braking force, steering moment of resistance and steering torque get smaller with the increase of the turning radius. The research results can provide theoretical basis for the design and application of the screw-driven vehicle and it is significant for guiding the engineering practice.
screw-driven vehicle; steering performance; kinematics; dynamics; simulation
1672-1497(2015)02-0047-05
2014-06-23
郭曉林(1974-),男,副教授,博士。
U463.4
A
10.3969/j.issn.1672-1497.2015.02.009

