拓展映射法求非線性偏微分方程的新解

何紅生

（集美大學(xué)理學(xué)院，福建廈門 361021）

拓展映射法求非線性偏微分方程的新解

何紅生

（集美大學(xué)理學(xué)院，福建廈門 361021）

構(gòu)建了一種拓展的映射法（F展開法）求解某些非線性偏微分方程（PDEs）的精確解.研究表明，該拓展的映射法不僅能夠求得方程的Jacobi橢圓函數(shù)的整數(shù)冪指數(shù)形式解，而且能夠求得非線性方程的分?jǐn)?shù)冪指數(shù)形式（1＋δf2（ξ））1／2的Jacobi橢圓函數(shù)解.

拓展的F展開法；Jacobi橢圓函數(shù)；耦合Klein-Gordon-Schr?dinger方程

0 引言

非線性方程是解釋大多數(shù)非線性物理現(xiàn)象的重要方法，所以，求解非線性物理方程的精確解是很有意義的研究課題.在過(guò)去的幾十年里，研究者們發(fā)展了大量有效的方法來(lái)求解非線性方程的精確解，比如：反散射法［1］、Backlund變換［2］、Darboux變換［3］、截?cái)郟ainleve展開法［4］、Hirota雙線性法［5］、正弦-余弦法［6］、雙曲正切函數(shù)法［7］、齊次平衡法［8-9］，等等.眾所周知，橢圓函數(shù)（如Jacobi橢圓函數(shù)和Weierstrass橢圓函數(shù)等）與非線性偏微分方程有著密切的關(guān)系［10-12］.而且，研究［13-15］表明，很多非線性方程有橢圓函數(shù)解.近年來(lái)逐漸發(fā)展起來(lái)的映射展開法［16-17］可以求得Jacobi橢圓函數(shù)解，并且在極限情況下可分別求得方程的孤立波和三角函數(shù)周期解.本文將構(gòu)建一種拓展的映射展開法，并用于求解耦合的Klein-Gordon-Schr?dinger（K-G-S）方程.

1 拓展的映射展開法

考慮一非線性偏微分方程形式如下：

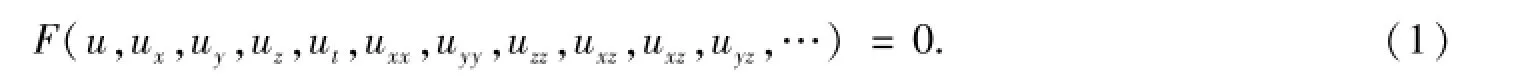
首先假定方程以下形式的行波解：

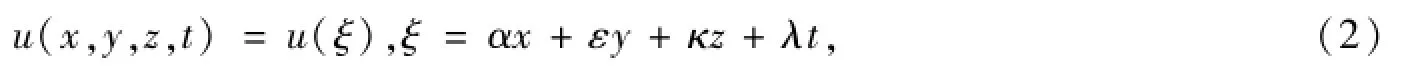
則方程（1）變?yōu)榉蔷€性常微分方程：

假設(shè)方程（3）有以下形式的解：

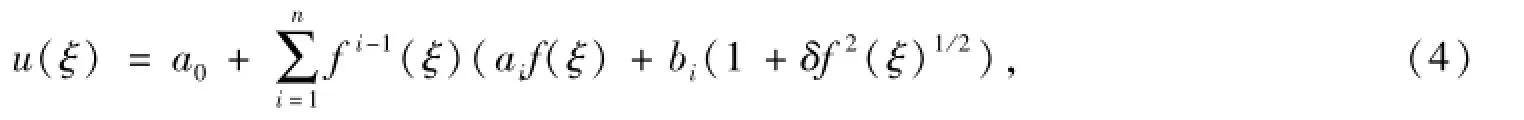
其中：a0，ai，bi，δ（δ≠0）為待定的系數(shù)；n為由方程的最高階線性導(dǎo)數(shù)項(xiàng)和最高階非線性項(xiàng)決定的齊次平衡數(shù)；f（ξ）滿足以……