基于進化博弈的水利工程施工安全監督管理

高 亞,章恒全

(河海大學商學院,江蘇南京 211100)

基于進化博弈的水利工程施工安全監督管理

高 亞,章恒全

(河海大學商學院,江蘇南京 211100)

為了探討影響水利工程建設施工安全監督管理行為的因素,分析施工監督管理進化穩定策略,在水利工程建設監理單位和施工承包商具有有限理性的前提下,運用博弈論方法,構建了基于進化博弈的水利工程建設監理單位和施工承包商的博弈模型。對進化博弈穩定策略的分析結果表明:水利工程建設監理單位對水利工程建設施工安全監督管理的策略選擇主要和嚴格監督管理成本與獎勵、監督管理失誤率、監督管理可能受到的懲罰等有關;施工承包商對水利工程嚴格施工的策略選擇主要和嚴格施工成本與獎勵、不嚴格施工可能受到的懲罰等有關;水利工程建設監理單位和施工承包商之間的進化博弈穩定策略與各影響因素的初始值有關。最后運用Matlab軟件進行數值仿真,模擬博弈雙方之間的動態博弈過程,并提出加強我國水利工程建設施工過程中安全監督管理的建議。

水利工程;施工安全監督管理;進化博弈;進化穩定策略

一般而言,與房屋建筑工程相比,水利工程規模龐大,施工技術復雜,工期長,且建成后需要定期維護,保證工程正常運行。水利工程一般修建在地形比較特殊的地方,如靠山修建,加大了施工的難度。同時,水利工程建筑物構造比較特殊,需要專業施工技術人員,施工技術難度加大了水利工程施工事故發生的風險性。

在水利工程建設過程中,施工總承包商往往會按專業、作業空間分布等方式將工程“合理”分包,以此達到工程質量、進度和投資的綜合效益最大化[1]。施工總承包商在對工程進行分包及施工過程中,總承包商及分包商的行為都會影響業主的利益,因此業主會選擇專業的監理單位對施工總承包商的行為進行監督,以減少自己的損失。Guanselaran等[2]認為施工總承包商和分包商是相互獨立和理性的個體,每個個體受自身利益最大化的驅使,會選擇實現局部最優。施工承包商和監理單位作為理性的個體,往往也會選擇對自身利益有利的行為。施工總承包商在施工過程中,為追求自身利益最大化,有可能犧牲業主的利益,選擇分包商及施工時不按水利工程施工標準進行。由于水利工程施工的特殊性,尤其是隱蔽工程的事后檢查難度很大,監理單位在監督過程中可能會選擇嚴格監督檢查,保證不出現不良工程;但監理單位若追求自身利益最大化,也有可能選擇與承包商“合作”。

相關學者對水利工程施工質量控制方面進行了研究。王國強等[3]構建監理單位和施工承包商之間的博弈模型,分析水利工程施工階段質量控制的對策選擇。王旭華等[4]構建承包商、監理和業主三方博弈模型,分析三方在水利工程質量管理方面的對策選擇問題。王賀瑤等[5]構建業主和監理單位的委托代理模型,分析兩者策略選擇問題。關于水利工程建設安全監督管理的博弈問題研究主要集中在建筑業,如申玲等[6]根據建筑工程承包商和政府之間的博弈關系,構建雙方的博弈監督管理模型。同時,進化博弈方法被廣泛應用于其他工程,如劉德海等[7]將進化博弈應用于煤炭工業,構建煤炭工業和政府監督管理機構之間的進化博弈模型,分析博弈雙方的初始影響因素等。

綜上所述,對水利工程建設中相關利益主體的博弈分析相對較多,但研究中很少有運用進化博弈分析水利工程建設監理單位和施工承包商之間的博弈問題,尤其是兩者之間的安全監督與安全施工的博弈問題。水利工程建設施工過程中最直接的利益主體就是業主、施工承包商和建設監理單位,但與施工安全事故有直接聯系的是建設監理單位和施工承包商。本文根據相關資料,以水利工程建設監理單位和施工承包商為博弈主體,構建進化博弈模型,分析水利工程施工安全方面的博弈問題。

1 水利工程建設施工安全監督管理進化博弈模型構建

1.1 模型假設

1.1.1 博弈方假設

由于水利工程建設施工安全監督管理涉及的相關利益主體較多,本文考慮的博弈主體為水利工程建設監理單位和施工承包商。假設博弈雙方為有限理性行為人,且雙方沒有發生“共謀”,監理單位不會接受施工承包商的賄賂,雙方不發生尋租問題等。

1.1.2 策略假設

在博弈方有限理性的前提下,水利工程建設監理單位和施工承包商追求利益最大化。將博弈雙方的策略抽象為具體行為。假設水利工程建設監理單位的策略集為:A1={嚴格監督管理,不監督管理},施工承包商的策略集為:A2={嚴格施工,不嚴格施工}。

1.1.3 得益假設

博弈方追求的最終目標及行為選擇和判斷的主要依據是博弈的最終結果,即博弈的得益[8]。本文對水利工程建設監理單位和施工承包商博弈雙方的得益假設如下。

a.建設監理單位的得益假設:建設監理單位正常收入為I1,嚴格監督管理施工承包商施工過程的成本為C1;當施工承包商不嚴格施工時,建設監理單位在嚴格監督管理過程中會有一定的失誤率e,即當施工承包商不嚴格施工且建設監理單位監督管理不到位時,建設監理單位受到一定的懲罰(直接經濟損失等)F1;當施工承包商不嚴格施工且被建設監理單位發現時,建設監理單位得到一定的獎勵(直接經濟獎勵等)R1。

b.施工承包商的得益假設:施工承包商的正常經營收入為I2,嚴格施工時的投入成本為C2,且在建設監理單位監督管理時,若其嚴格施工且無事故發生,會得到一定的獎勵(直接的經濟獎勵等)R2;若承包商不嚴格施工,被建設監理單位發現時,不管是否發生安全事故,懲罰F2(直接經濟懲罰等)。假設施工承包商嚴格施工就不會發生安全事故。

1.1.4 博弈過程

本文的博弈分析框架為兩個有差別的有限理性博弈方群體,相互之間隨機配對進行博弈,且博弈雙方得益不對稱,即基于進化博弈的非對稱博弈分析。

1.2 模型構建

根據上述假設,得到水利工程建設監理單位和施工承包商的得益矩陣(見表1)。

表1 2×2非對稱博弈得益矩陣

假設博弈方1所在位置的博弈群體中,博弈方1采取“嚴格監督管理”策略的比例為x,那么采取“不監督管理”策略的比例為1-x;假設博弈方2所在位置的博弈群體中,采取“嚴格施工”策略的比例為y,那么采取“不嚴格施工”策略的比例為1-y。

建設監理單位嚴格監督管理的期望得益為

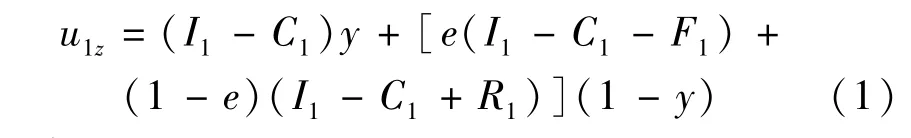
建設監理單位不監督管理的期望得益為

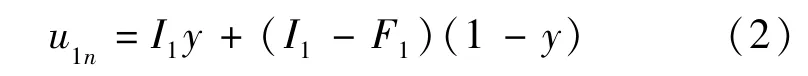
建設監理單位的平均期望得益為

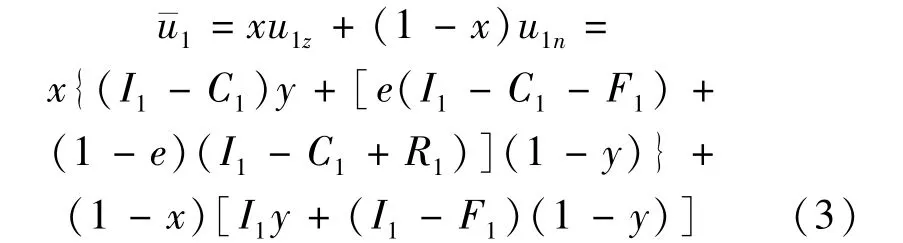
建設監理單位采取“嚴格監督管理”策略的復制動態方程為

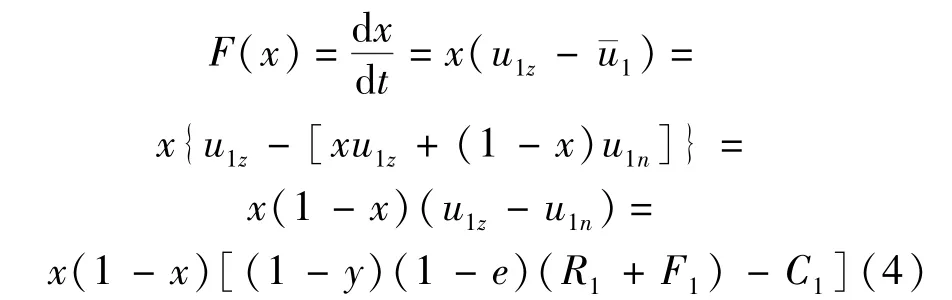
同理可得:施工承包商采取“嚴格施工”策略的復制動態方程為

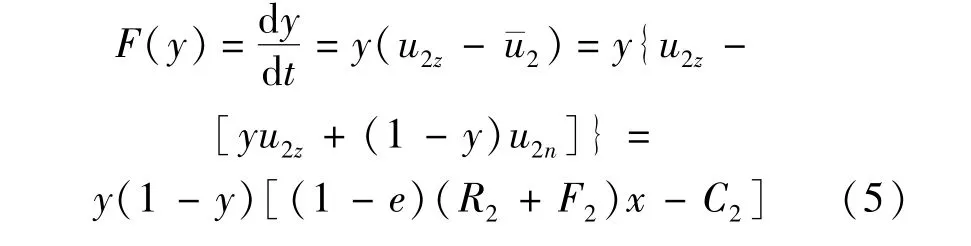
2 水利工程建設施工安全監督管理進化博弈模型分析

2.1 建設監理單位策略進化穩定分析

一般情況下,假設C1＜I1,R1＜F1,e很小。

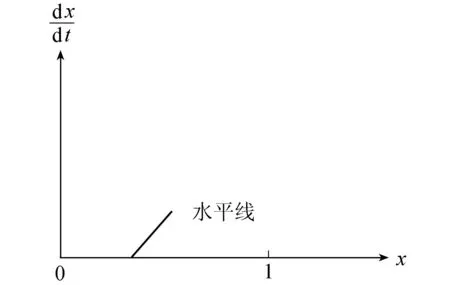
圖1時的復制動態相位

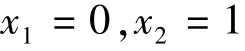
對F(x)求一階倒數得

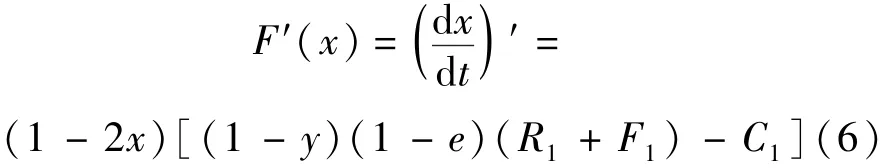
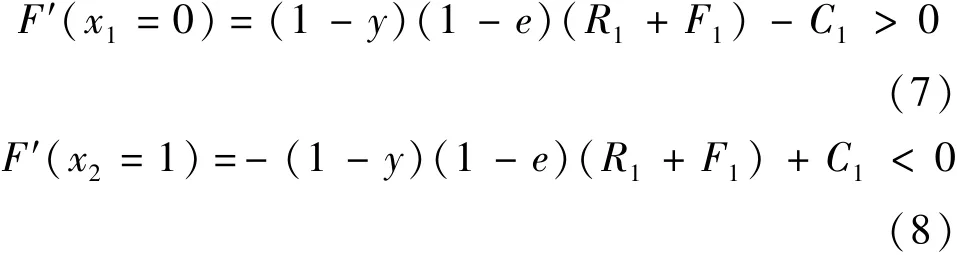
根據微分方程的“穩定性定理”可知:若F(x)的兩個穩定狀態為進化穩定策略,則F憶(x)＜0。所以x2=1為進化穩定策略(ESS)(見圖2)。

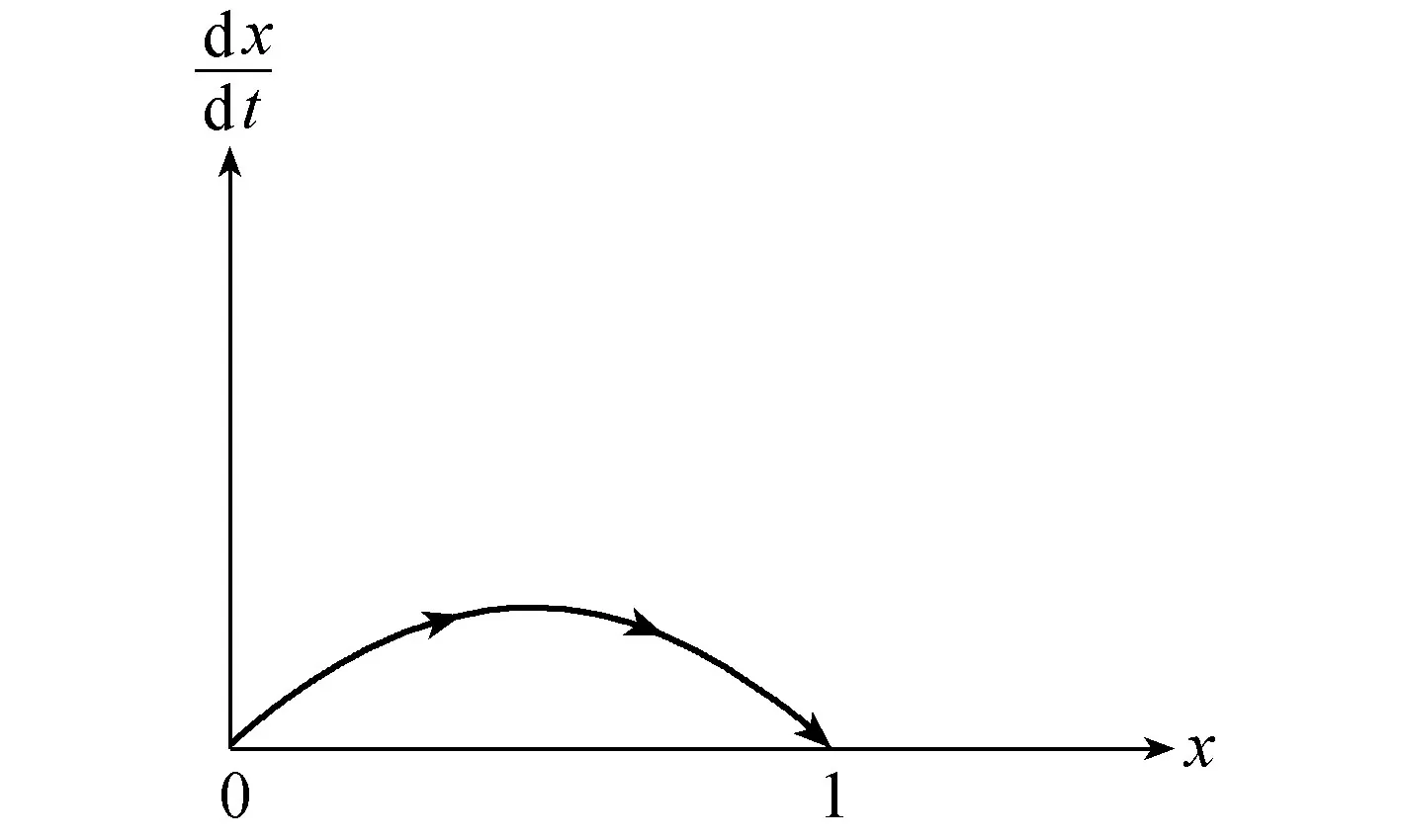
圖2時的復制動態相位

該博弈的雅克比矩陣為

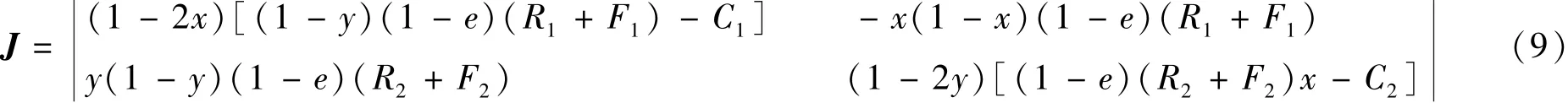
該博弈系統雅克比矩陣的行列式和跡分別為

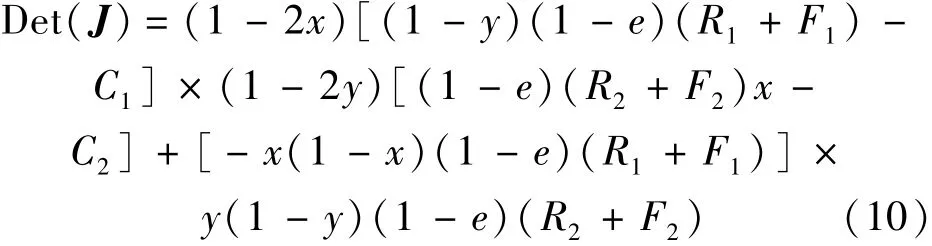
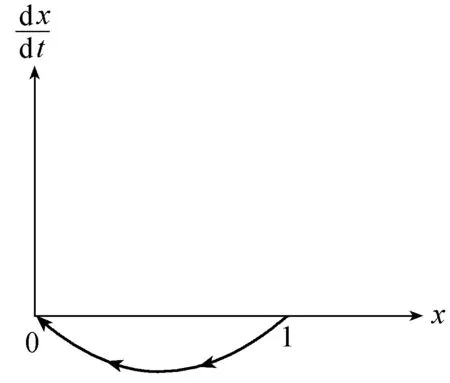
圖3時的復制動態相位

2.2 施工承包商策略進化穩定分析

一般情況下,假設C2＜I2,R2＜F2。

2.3 博弈雙方聯合策略進化穩定分析

將博弈雙方復制動態方程的微分方程聯立求得本博弈的5個均衡點,見表2。

表2 各均衡點的穩定性分析結果

由微分方程表示的系統的均衡點不一定是系統的穩定點,即均衡點未必是穩定點,均衡點的最終穩定性狀態可通過雅克比矩陣判斷。

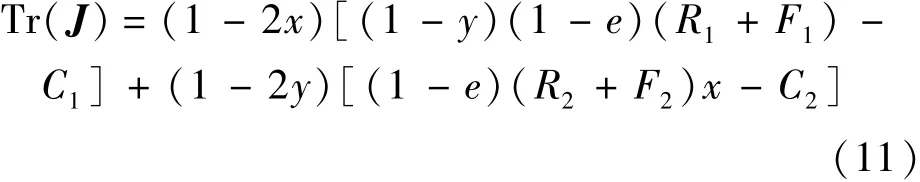
本文假設R1＜R2,C1＜C2,F1＜F2,R1＞C1,F1＞C1,R2＞C2,F2＞C2。

由表2可知,在上述假設條件下,水利工程建設監理單位與施工承包商博弈的進化穩定策略有3個,即:x1=0,y1=0;x1=0,y1=1和x2=1,y2=0。策略選擇分別為:水利工程建設監理單位采取“不監督管理”策略,施工承包商采取“不嚴格施工”策略;水利工程建設監理單位采取“不監督管理”策略,施工承包商采取“嚴格施工”策略;水利工程建設監理單位采取“嚴格監督管理”策略,施工承包商采取“不嚴格施工”策略。以上所得出的博弈雙方采取的策略主要是根據不同的初始值情況所采取的,初始值改變時,雙方采取的策略會隨之改變。

3 數值仿真

為了更清楚地解釋水利工程建設監理單位和施工承包商之間進化博弈的演變過程,本文對影響水利工程建設監理單位和施工承包商的策略選擇的因素指標進行賦值,并運用Matlab7.0[9]軟件進行數值仿真,模擬進化博弈演變過程。

令e=0.2,R1=5,R2=7,C1=3,C2=4,F1=4,F2=5,將各值代入式(4)和(5)中得

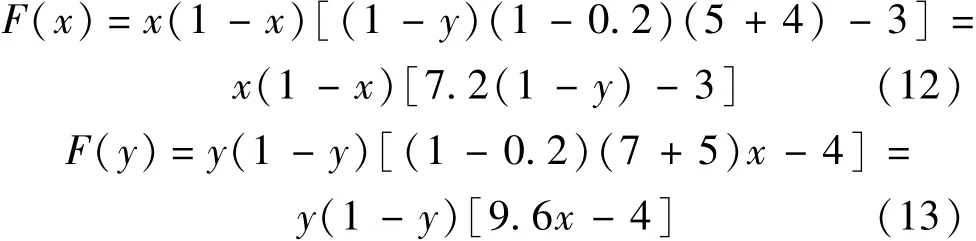
a.建設監理單位選擇“嚴格監督管理”策略比例分別取x=0.7和x=0.3。

繪制施工承包商在不同初始比例的“嚴格施工”策略下的動態博弈過程(見圖4)。

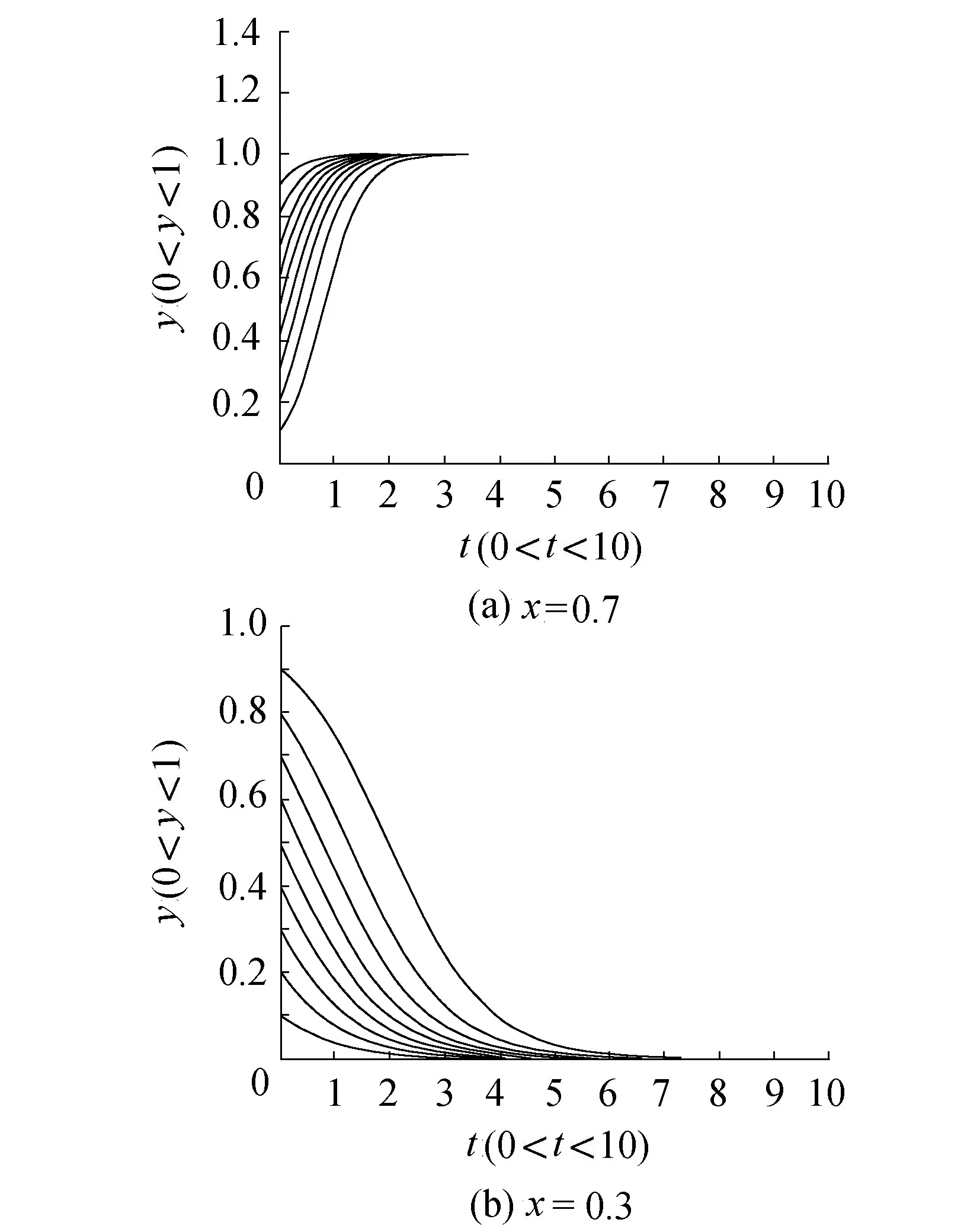
圖4 施工承包商策略選擇隨博弈時間變動的演化過程

由圖4(a)可知,當建設監理單位策略選擇x＞0.5時,在不同的初始“嚴格施工”策略比例下,施工承包商選擇“嚴格施工”的比例都會收斂到1,即施工承包商最終會選擇“嚴格施工”策略。

由圖4(b)可知,當建設監理單位策略選擇比例x＜0.5時,在不同的初始“嚴格施工”策略比例下,施工承包商選擇“嚴格施工”的比例都會收斂到0,即施工承包商最終會選擇“不嚴格施工”策略。

b.施工承包商選擇“嚴格施工”策略比例分別取y=0.7和y=0.3。繪制建設監理單位在不同比例的“嚴格監督管理”策略下的動態博弈過程(見圖5)。

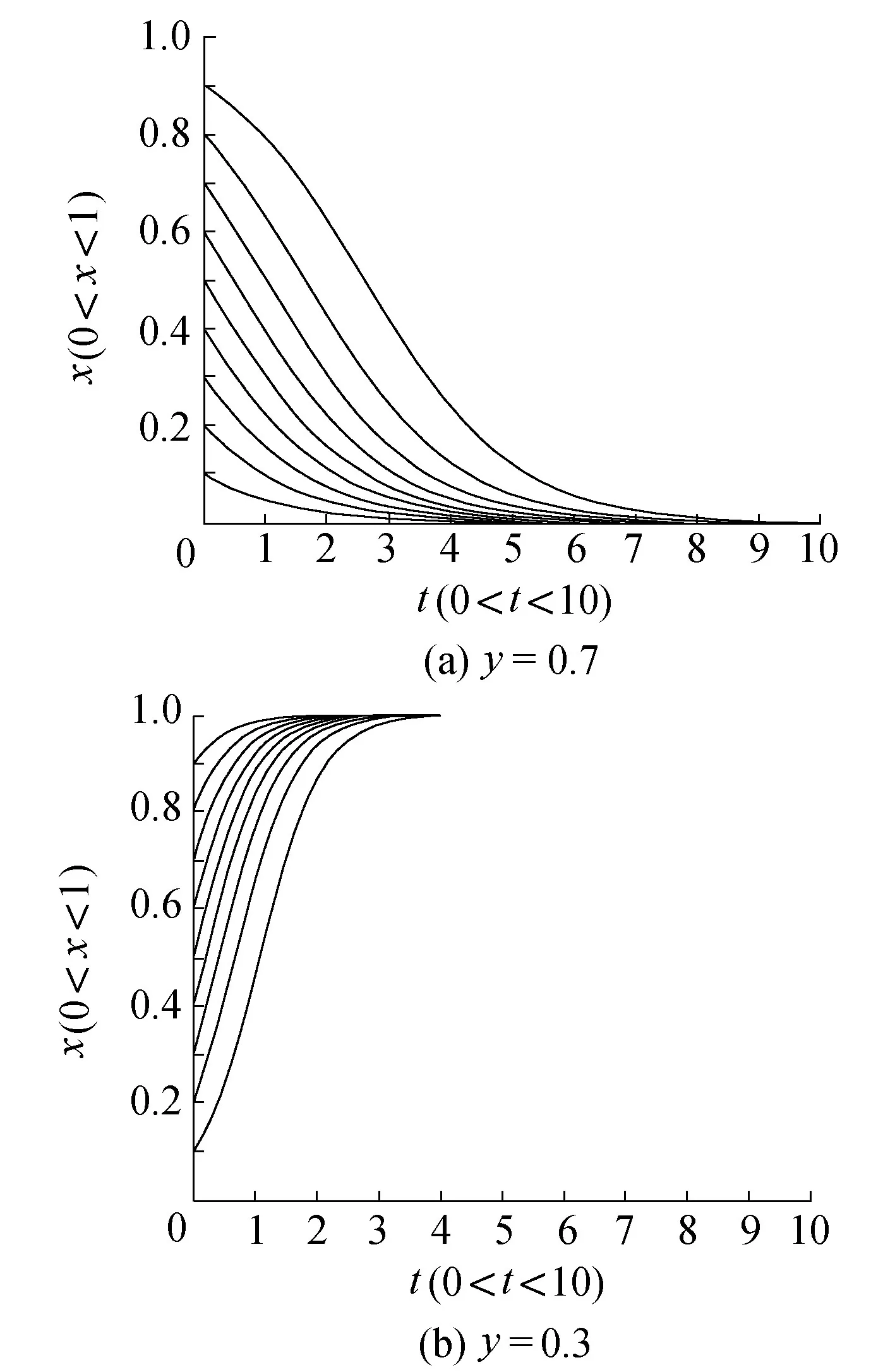
圖5 建設監理單位策略選擇隨博弈時間變動的演化過程

由圖5(a)可知,當施工承包商策略選擇y＞0.5時,在不同的初始“嚴格監督管理”策略比例下,建設監理單位選擇“嚴格監督管理”的比例都會收斂到0,即建設監理單位最終會選擇“不監督管理”策略。

由圖5(b)可知,當施工承包商策略選擇比例y＜0.5時,在不同的初始“嚴格監督管理”策略比例下,建設監理單位選擇“嚴格監督管理”的比例都會收斂到1,即建設監理單位最終會選擇“嚴格監督管理”策略。

c.繪制水利工程建設監理單位和施工承包商之間的進化博弈動態過程,見圖6。

由圖6可知,水利工程建設監理單位和施工承包商之間的進化博弈一直處于動態過程,博弈雙方都會根據對方的策略選擇動態地改變自己的策略選擇。

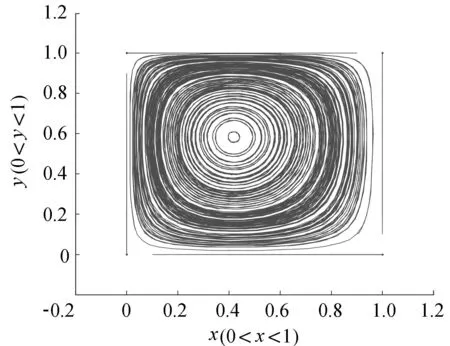
圖6 博弈雙方進化博弈動態過程

4 結 語

[1]郜軍艷,聶相田,王博.水利工程建設施工供應鏈質量控制博弈研究[J].水電能源科學,2012,30(9):115-118

[2]GUANSELARAN A,PATER C,MCGAUGHEY R E.A framework for supply chain performance measurement[J]. International Journal of Production Economics,2004,87 (3):333-347.

[3]王國強,周書杰,李鵬,等.基于博弈論的監理人水利工程施工階段質量控制[J].水利經濟,2010,28(2):59-61.

[4]王旭華,張春華,王南江.水利工程建設質量管理的博弈研究[J].治淮,2012(5):42-44.

[5]王賀瑤,姜國輝,佟國紅,等.水利工程中的業主和監理之間的委托代理博弈模型[J].安徽農業科學,2007,35 (3):920-921.

[6]申玲,孫其珩,吳立石.基于博弈關系的建筑安全投入監管對策研究[J].中國安全科學學報,2010,20(7):110-115.

[7]LIU Dehai,XIAO Xingzhi,LI Hongyi.Historical evolution and benefit-costexplanation of periodical fluctuation in coal mine safety supervision:An evolutionary game analysis framework[J].European Journal of Operational Research, 2015,243(3):974-984.

[8]謝識予.經濟博弈論[M].3版.上海:復旦大學出版社, 2013.

[9]徐金明.MATLAB實用教程[M].北京:清華大學出版社,北京交通大學出版社,2005.

TV523

A

1003 -9511(2015)04 -0072 -05

2015-04 -13 編輯:胡新宇)

10.3880/j.issn.1003 -9511.2015.04.018

高亞(1991—),女,江蘇宿遷人,碩士研究生,主要從事管理科學與工程研究。E-mail:1584091323@qq.com