基于動態規劃原理的房地產項目多階段資金分配研究Multi-stage allocation funds for real estate project based on dynamic programming

文/任華茜 西南科技大學土木工程與建筑學院 四川綿陽 621010

REN Huaqian Southwest University of Science and Technology, MianYang621010,China

基于動態規劃原理的房地產項目多階段資金分配研究Multi-stage allocation funds for real estate project based on dynamic programming

文/任華茜 西南科技大學土木工程與建筑學院 四川綿陽 621010

REN Huaqian Southwest University of Science and Technology, MianYang621010,China

房地產資金分配問題中，本文以動態規劃的方法為基礎將問題考慮為一個多階段的資金分配問題來研究，在此基礎上同時考慮項目的風險-收益對資金分配的影響。通過分析預測收益、風險衡量，尋求在風險-收益達到一定平衡最優的情況下再進行資金分配，建立馬爾可夫決策模型。討論了模型的假設條件，并結合實例，得到最優資金分配方案。

1、引言

動態規劃是研究多階段決策過程最優化問題的一種數學方法。早在50年代初，美國數學家R.貝爾曼首先提出了動態規劃的概念。隨后，人們致力于將動態規劃理念運用于各個行業特別是房地產資金分配方面。文獻[4-5]針對在單一投資階段中的資產投資組合問題的投資決策研究，現在已有不少成熟的模型和結論。然而對于在房地產多階段中的資金分配問題方面進行研究討論的還比較少。這里提到的一個階段是指一個投資階段中，投資者從一次資產投資決策開始，到下一次資產投資決策之前的這段時間，也就是指一次投資決策的持續時間。文獻[6]針對多階段資產投資問題，討論了多階段投資模型與單階段投資模型的關系。文獻[7]研究了當終止時間不確定時的多階段最優投資組合問題，應用動態規劃求解模型，得到最優投資策略以及有效邊界的解析形式。文獻[8]針對多階段風險投資，構建了多階段投資總體概念模型。

房地產項目多階段的資金分配問題研究的是，房地產投資者在連續的幾個投資階段中的每個階段里都進行資金分配決策，其目的是到最后一個投資階段結束時，投資者進行多次資金分配的收益總和盡可能大、或總風險盡可能小、亦或者是使收益和風險二者同時達到最優的情況。在這樣的多階段資金分配中，如果這些資金分配階段之間都是沒有關系的，那么多階段的資金分配決策就可以簡單地機械地分為多個單階段的資金分配相加的情況來處理；而如果這些資金分配階段之間是有相互關聯的，多階段資金分配問題就要比單階段資金分配問題的簡單加和要復雜得多。在實際項目中，由于對同一個投資者來說，一般會對風險資產進行多次投資，而且由于資金來源等條件的限制，其在多次投資中的資金分配決策往往是有關系的。因此，對各階段的資金分配間有關系的多階段資金分配決策問題進行研究是很有必要的。

但是以往文獻基本只考慮了房地產資金分配中的個別影響因素。由于房地產投資是一個復雜且影響因素眾多的系統項目，比如現實中利率是隨機變化的，世界各國經常根據國內外經濟環境、政治環境和政策需要而調整利率。所以在長期投資決策過程中，并不存在真正意義上的無風險資產。所以多階段投資風險分析是必不可少的，在此基礎上投資者最關心的投資收益率問題也是需要共同考慮的。故本文基于動態規劃理論，運用馬爾可夫決策中序貫決策問題來研究房地產投資收益率及風險系數之間的關系并考慮稅收還貸情況下的房地產項目多階段資金分配問題。序貫決策問題是適用于隨機性或不確定性動態系統最優化的決策方法。所研究的系統是動態的，即系統所處的狀態與時間有關，可周期（或連續）地對它進行觀察；每個時刻根據所觀察到的狀態和以前狀態的記錄，從一組可行方案中選用一個最優方案作最優決策，使取決于狀態的某個目標函數取最優值（極大或極小值）；基于此優點及適用條件，序貫決策問題對于本文所研究的房地產項目多階段的資金分配問題是適用的。

本文結構如下：第2節是模型構建，融入收益率及風險系數因素，構建了馬爾可夫決策模型；第3節數值算例；第4節是本文的結論。

2、模型的構建

2.1為簡化問題的考慮,建立以下五點假設

1.投資者只在投資開始時(即第1階段初)向資產市場投入一定數額的自由資金，在其后的N-1個階段中不再增加對該資產市場的資金投入；同時，也不把已獲得的收益資金從資產市場中抽出。也就是說，投資者的最終持有的資產和資金只是由最初的自由資金進行了N次投資后獲得的。

2.在資產投資中，不允許賣空行為，即投資者的銷售量不允許超過其當時的實際資產持有量。

3.其中假設過去投資機會W的出現與否相互獨立，即每個階段的投資機會出現概率互不影響。

4.一般來說投資越分散，投資風險就越小，基于此情況，我們確定投資總風險用各階段中所投資的各種資產風險中最大的一個來衡量。而且，投資者的投資風險要求不能高于一個固定的風險上限。

5.投資是持續的，在相鄰兩階段間沒有其他投資行為。這樣，任一階段結束時投資者的資產及自由資金情況與下一階段初時的情況相同。也就是說已用于投資的資金以及因投資獲得的報酬R(y)都不再用于后續周期的投資。

2.2馬爾可夫決策模型構建

假定R(y)為非降凹函數且R(0)=0。

記Vn(A)表示投資者用于投資的剩余資金為A元，還有n個階段且投資機會出現時所能獲得的最大期望總報酬，則Vn滿足如下最優方程：

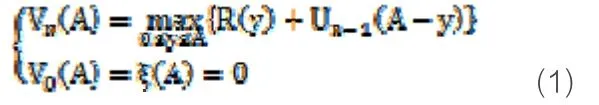
其中

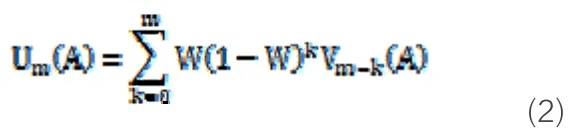
式中：投資金為y，在N個階段結束時獲得報酬R(y)，每個階段投資機會的概率為Wi。

表示在一定條件下的最大期望總報酬：用于投資的剩余資金為A，剩余投資階段還有m個，不知道目前是否還有投資機會。顯然

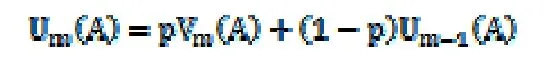
為從我們的最優方程（1）中得到最優策略，我們需要對于每個n，A，都有y取到其中的最大值。

首先要證明Vn均是凹函數。即對任意的n，Vn(A)為A的凹函數。

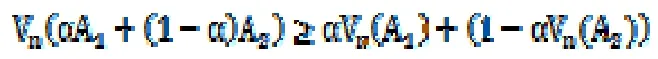
現按常例假設yn(A)為最優方程取值中的最小值，即

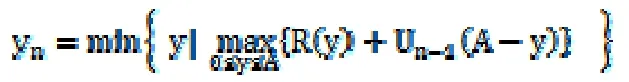
表示用于投資資金A，還剩余n個階段，在出現投資機會條件下的最優投資量。

2.3多階段資金分配的收益和風險模型

1.多階段投資的期望收益率。由項目各階段的期望收益率的加權平均數構成，其表達式為：

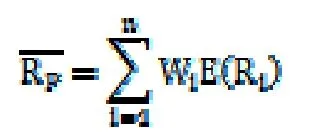
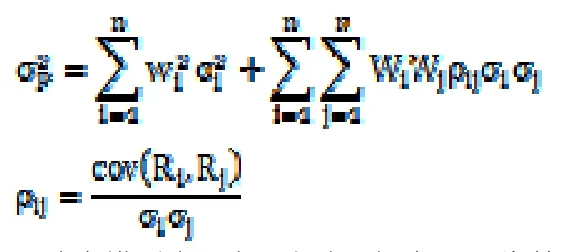
3.建立模型由于有N個階段投資，Wi為第i階段投資機會概率，Ri為收益率，為總體風險，建立模型：

3、數值算例

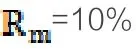
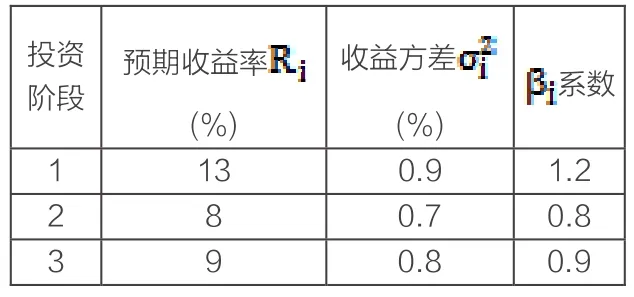
表1 -投資項目各階段投資參數

現將各階段投資機會概率Wi帶入模型求解，得：

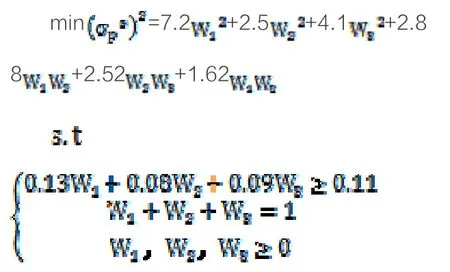
結果表明該投資項目的三個階段投資概率分別為0.528，0.112，0.360時項目的收益與風險達到了最優情況，風險將遠遠小于一次性投資，起到了風險分擔的作用。

再由式子（1）（2）有：

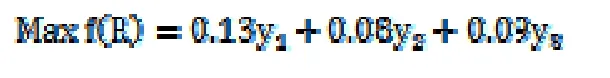
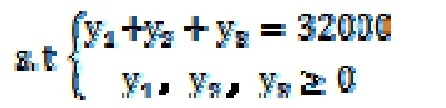
即投資者將在第1階段分配資金19968萬元，第2階段分配資金2608萬元，第3階段分配資金9424萬元。按此比例分配資金將在風險盡可能小的情況下收益達到最大化。

4、結論

通過以上對房地產多階段資金分配最優模型的研究，說明資金的分配分為多階段后不僅將增加投資者的收益，而且能大大降低其風險。其次，將風險-收益作為投資者資金分配前特別考慮的因素量化，與多階段分配綜合研究后進行的資金分配將更貼近現實情況，能盡可能的幫助投資者規避風險獲得更大的收益。

[1]滕宇,梁方楚.動態規劃原理及應用[M].成都:西南交通大學出版社,2011.

[2]胡運權.運籌學教程（第三版）[M].北京:清華大學出版社,2010.

[3]胡奇英,劉建庸.馬爾可夫決策過程引論[M].西安:西安電子科技大學出版社,2000.

[4]Alexande,G,J,Sharpe,W,F.F.Funda mentals of Investments [J]. Prentice-Hall Inc,1989, 12(3): 132-140.

[5]徐大江.證券投資決策的多目標線性規劃方 法 [J].系 統 工 程 理 論 與 實 踐 ,1995, (12):46-52.

[6]宿潔,劉家壯.多階段資產投資的動態規劃決策模型[J].中國管理科學,2010,9(3):55-61.

[7]郭文旌,胡奇英.不確定終止時間的多階段最優投資組合[J].管理科學學報,2005, 8(2):13-19.

[8]陳曉慧,魏文娟,段鷹.風險投資多項目多階段投資組合決策研究[J].價值工程, 2009, (7):106-109.

Real estate funds allocation, the paper-based method of dynamic programming problems will be considered for allocation of funds to a multi-stage research, on this basis, taking into account the risk of the project - the impact on income distribution of funds. Through analysis and forecast earnings, risk measurement, risk seeking - income reaches a certain balance in the case then the best allocation of funds to establish a Markov decision model. Model assumptions are discussed, with examples, the optimal allocation of funds.

動態規劃；多階段；資金分配

dynamic programming；multi-stage；allocations