含有磁滯逆的狀態反饋非線性系統動態面控制

吳金龍

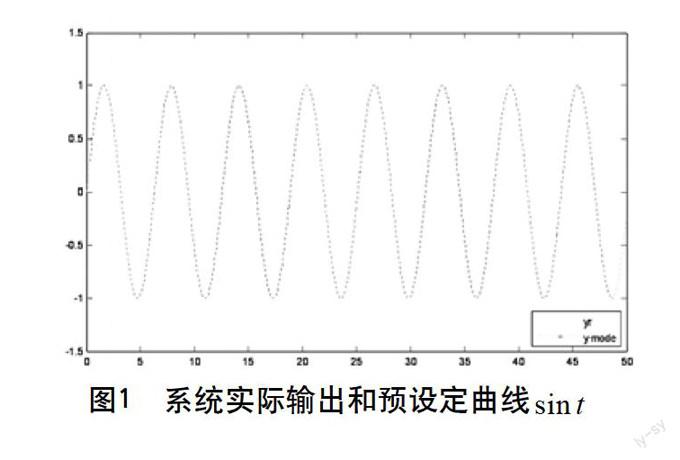
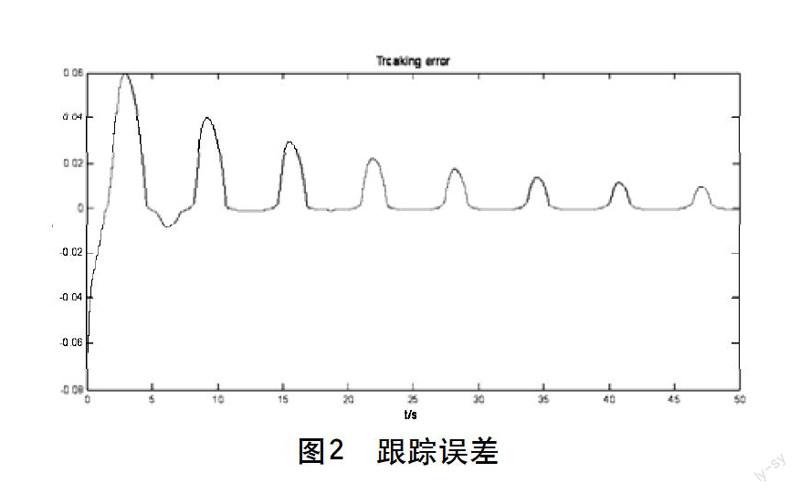
摘要：針對一類帶有Revised Prandtl-Ishlinskii（RPI）磁滯的嚴格狀態反饋非線性模型，通過引入磁滯逆模型抵消輸入中的磁滯輸入項，提出了一種改進的魯棒自適應動態面控制方案。本方案解決了采用反推法時出現的“微分膨脹”問題，保證閉環非線性系統所有信號半局一致有界。仿真結果證明了控制律的有效性。

關鍵詞：磁滯逆；動態面控制； 性能

中圖分類號：TP13 文獻標識碼：A 文章編號：1672-3791（2015）10（a）-0000-00

0引言

磁滯是一種常見的非線性現象，很多智能材料制作的裝置中都會出現，比如壓電陶瓷驅動器[1]。磁滯現象的存在制約了閉環控制系統的精確度和穩定性，容易產生震蕩[2]。由于現代工業大規模采用以智能材料為核心部件制作的裝備，因此系統中的非線性磁滯現象受到國內外學術界的廣泛關注[3]。

反推法在非線性系統中常被用來設計控制器。但是反推法在設計高階系統控制器時會出現“微分膨脹”問題，并且給計算機帶來極大的計算量。

在處理磁滯問題時，有魯棒自適應[4]和建立磁滯逆模型[5， 6]兩種方法，由于建立磁滯逆模型對于模型的精確性要求較高并且推導復雜，所以大部分學者采用魯棒自適應方法來克服系統中的磁滯現象，本文采用構造磁滯逆的方法來解決非線性系統的控制問題。通過設計合適的Lyapunov函數，保證閉環系統所有信號一致有界。仿真結果表明所設計的控制器具有較好的跟蹤性能。

參考文獻：

[1]谷國迎， "壓電陶瓷驅動微位移平臺的磁滯補償控制理論和方法研究，" 博士， 上海交通大學， 2012.

[2]Z. Xiuyu， W. Jing， and L. Cuiping， "Robust adaptive dynamic surface control for metal cutting system with hysteresis input，" in Intelligent Control and Automation （WCICA）， 2014 11th World Congress on， 2014， pp. 1534-1539.

[3]曹淑瑛， "超磁致伸縮致動器的磁滯非線性動態模型與控制技術，" 博士， 河北工業大學， 2004.

[4]賈濤， 劉軍， and 錢富才， "一類非線性時滯系統的自適應模糊動態面控制，" 自動化學報， pp. 83-91， 2011.

[5]L. Sining， S. Chun-Yi， and L. Zhi， "Robust Adaptive Inverse Control of a Class of Nonlinear Systems With Prandtl-Ishlinskii Hysteresis Model，" Automatic Control， IEEE Transactions on， vol. 59， pp. 2170-2175， 2014.

[6]L. Sining， S. Xinjun， L. Zhi， and S. Chun-Yi， "Inverse control of a class of nonlinear systems with modified generalized Prandtl-Ishlinskii hysteresis，" in IECON 2012 - 38th Annual Conference on IEEE Industrial Electronics Society， 2012， pp. 2319-2324.