基于單周期控制的雙Buck逆變器數字化控制研究

陳勛，林瓊斌，2，3

(1.福州大學電氣工程與自動化學院，福建 福州 350108;2.浙江大學電氣工程博士后流動站，浙江 杭州 310000;3.漳州科華電子博士后工作站，福建 漳州 363000)

1 引言

對于逆變器的研究，實現高效率和提高它的開關頻率是逆變器的重要研究內容。在許多情況下，高效率和高開關頻率是互相矛盾的，很難同時優化。傳統橋式逆變器的續流是通過體二極管來續流，而體二極管的性能較差，同時反向恢復時間長，這將導致很大損耗并限制了開關頻率的提高。而雙BUCK逆變電路的續流二極管不是開關管的體二極管，而是單獨的一個二極管，這樣可以使開關管和二極管分別優化設計。同時雙Buck逆變器拓撲能夠克服傳統橋式逆變器的開關管直通問題［1］。

本文基于雙Buck逆變器拓撲，對其數字化控制方式進行研究。與模擬控制不同的是，數字控制具有硬件電路簡單，抗干擾能力強，升級換代容易等優點，同時數字控制技術也是電源技術發展的必然趨勢。通常的雙Buck逆變器控制算法有基本PID控制、滯環電流控制、斜坡比較控制等。其中基本PID控制以其控制簡單、參數容易整定等優點被廣泛應用，但是單純的PID控制對于較為復雜的控制系統會難以勝任，所以經常和其他的一些控制方法相結合。滯環電流控制是一種很好的非線性控制方法，實現電路簡單，穩定性好，動態響應快，同時具有電流限制的能力，但是這種控制的開關頻率是不斷變化的，會導致濾波器難以進行選取［2］。斜坡比較控制是一種恒頻的線性控制，通過設置三角載波的頻率，時其與調制波進行交截，能夠很方便的控制開關管，但是這種控制需要額外加入最小偏置電流，造成濾波電感中始終有環流通過，導致逆變器效率難以提高。基于上述控制方法的優缺點，本文將采用雙環控制，內環基于單周期控制的電流控制算法，外環基于PI控制的方法對雙Buck逆變器拓撲進行數字化控制。單周期電流控制是數字控制特有的一種控制算法，這種控制算法能根據逆變器當前時刻的狀態方程和輸出電感電流反饋信號來計算當前開關周期的占空比，對系統參數變動反應靈敏，具有較好的穩態輸出特性。同時外環采用PI控制對采樣電壓與給定電壓的誤差進行控制，使輸出電壓的幅值與給定電壓較為穩定地變換。通過這兩種控制相結合的雙環控制，能夠很好的結合兩者的優點，克服兩者的缺點，使輸出電壓波形與給定電壓很好地進行跟蹤，輸出電壓波形質量更好，同時滿足較低的輸出電壓波形畸變率。

2 電感電流單周期控制算法

雙Buck逆變器拓撲工作時可分為四個工作模態，如圖1所示。(其中L1=L2=L)

模態1:開關管S1導通，S2關斷時(等效電路如圖1中模態1所示)，流過電感L1的電流線性增加，它的變化率為:

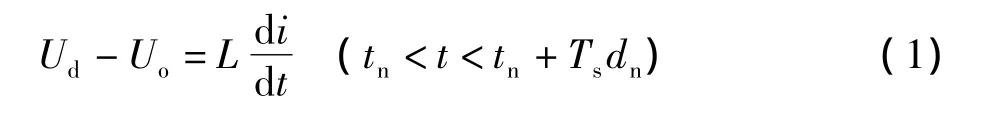
在此模態中，電感電流大小以(Ud－Uo)/L的斜率上升，此時的續流二極管是不導通。

模態2:開關管S1導通和S2都關斷時(等效電路如圖1中模態2所示)，此時續流二極管D1導通，流過電感L1的電流線性下降，它的變化率為:

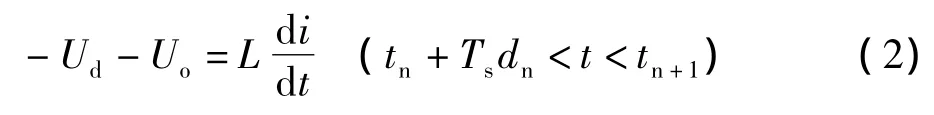
在此模態中，電感電流大小(－Ud－Uo)/L的斜率下降，續流二極管D1導通。

模態3:開關管S1關斷，S2導通時(等效電路如圖1中模態3所示)，流過電感L2的電流線性增加，它的變化率為:

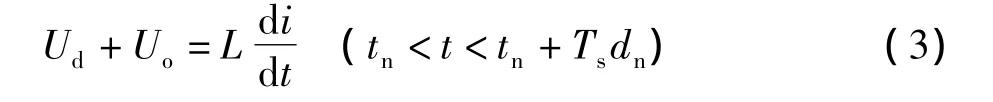
在此模態中，電感電流大小(Ud+Uo)/L以的斜率上升，此時的續流二極管D2不導通。

模態4:開關管S1和S2都關斷時(等效電路如圖1中模態4所示)，流過電感L2的電流線性減小，它的變化率為:

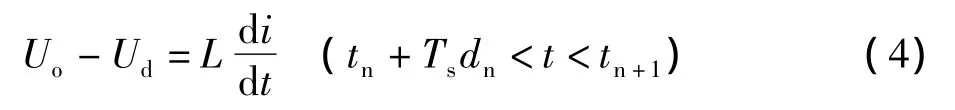
在此模態中，電感電流大小以(Uo－Ud)/L的斜率下降，此時續流二極管D2導通。

下面對每個開關周期的占空比公式進行推導，先對輸出正半周的模態1和模態2進行分析，可得如下關系式:

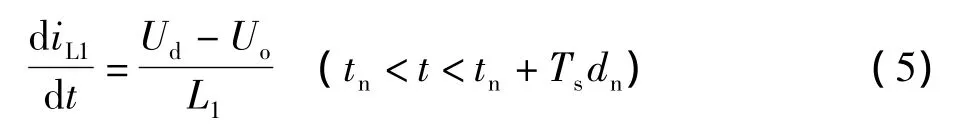
即

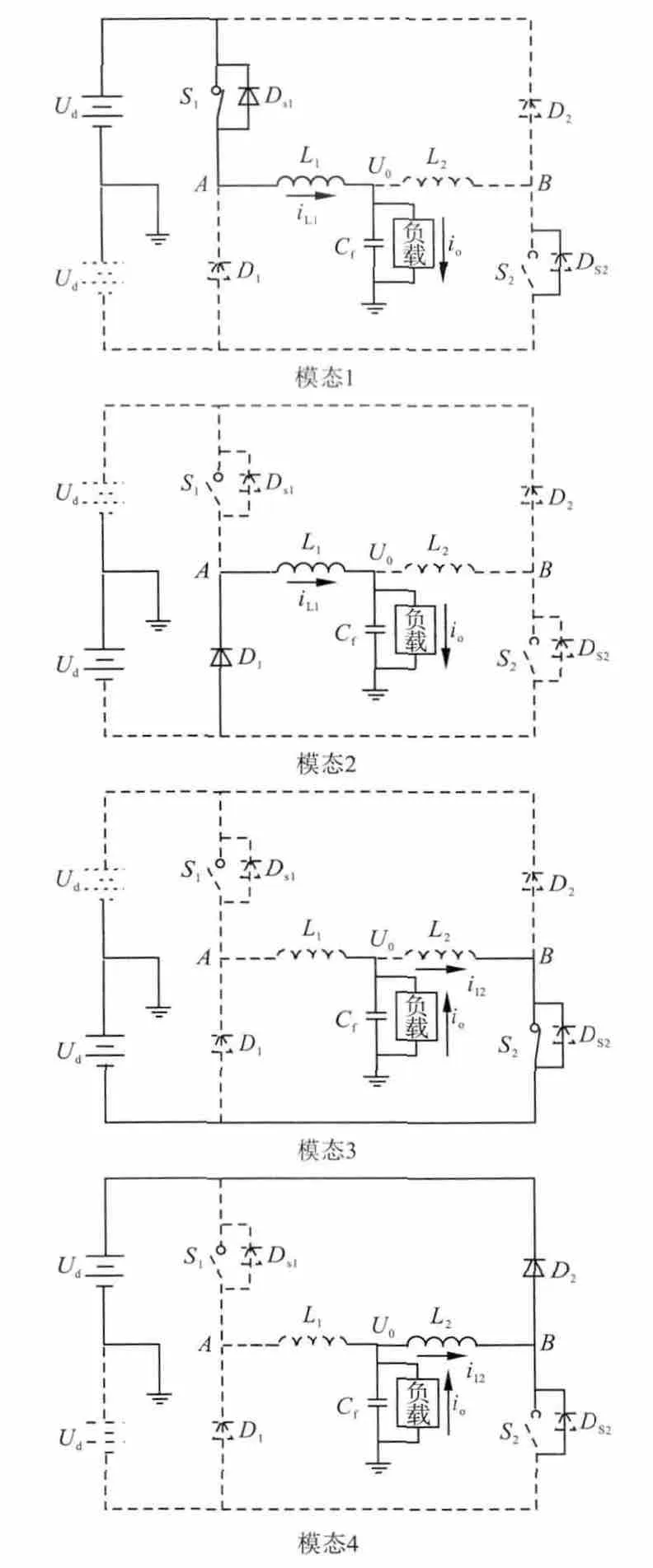
圖1 四種電路工作模態

可得電感電流iL1在第k個開關周期的S1導通期間內上升電流為:

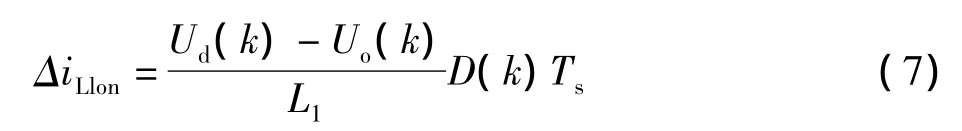
這是先由模態1所得，接下來根據模態2可得:

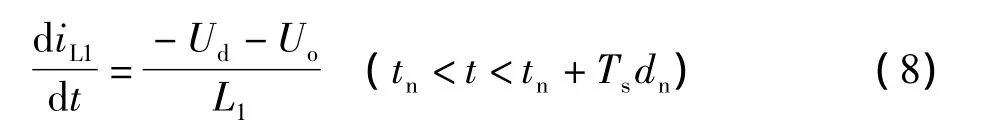
即

可得電感電流iL1在第k個開關周期的S1關斷期間內下降電流為:

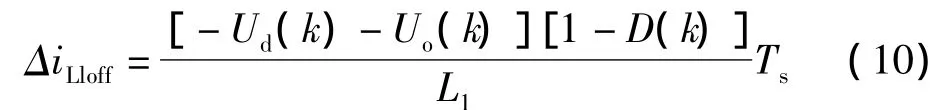
綜上可得第k個開關周期的電感電流變化量為:

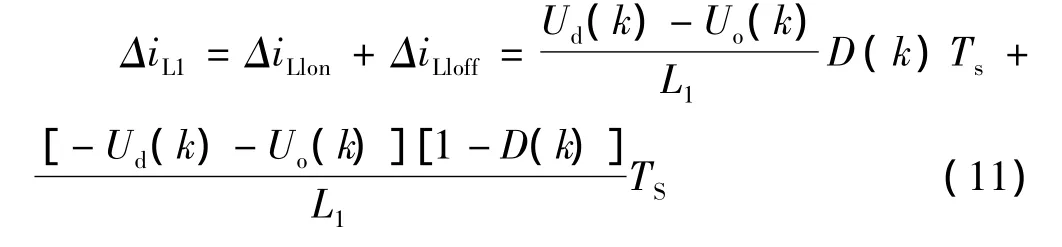
由上式可得占空比為:

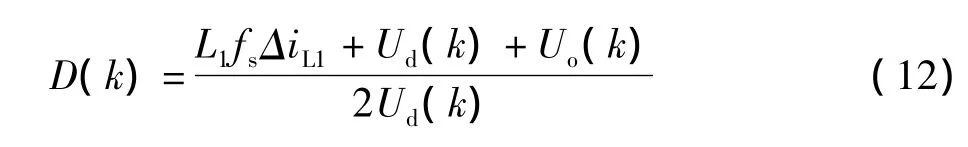
3 控制系統設計

本文的控制方式是基于外環PI內環單周期控制，同時內環單周期控制還具有預測電流的效果，能夠使電感電流很好地跟蹤下一拍預測的給定電流。基本控制系統框圖如圖2所示。

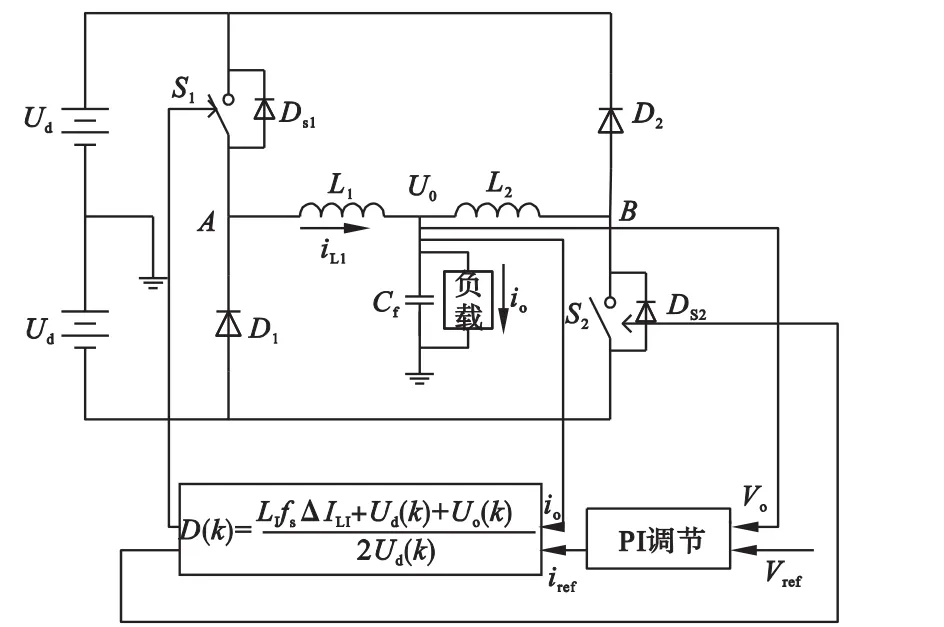
圖2 雙Buck拓撲控制系統框圖

電流內環控制的原理是基于單周期控制的思想，單周期控制能夠根據當前開關頻率、當前輸出電壓、輸入電壓和電感電流實時控制，每個開關周期的占空比的值都達到最佳，并且使被控對象的輸出信號在每個開關周期內的平均值等于參考值，在當前的開關周期內能夠消除此時的瞬態誤差，避免上一個開關周期的誤差累加到下一個開關周期，同時能夠有效地抗輸入側電壓擾動，具有很好的穩態和動態性能。內環電流算法即上一節推導的占空比公式。

電壓外環主要是穩定輸出電壓波形，本文中的外環采用基本PI控制算法，基本PI控制算法的公式如下所示:

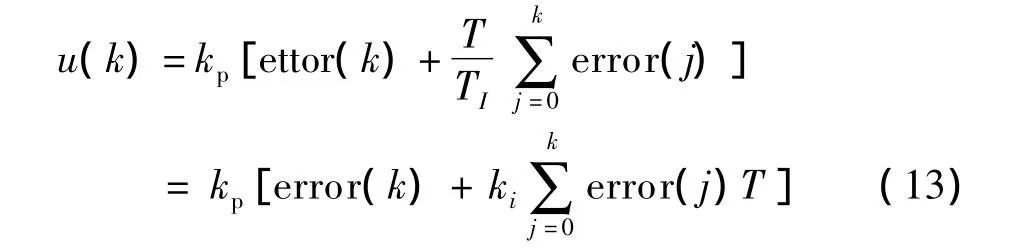
4 PSIM仿真分析

為了驗證上述算法的可行性，分別對PI外環，P內環和PI外環，單周期內環的算法分別進行空載、半載(500W)和滿載(1000W)的輸出電壓THD進行仿真分析。PSIM環境下的電路拓撲如圖3所示。

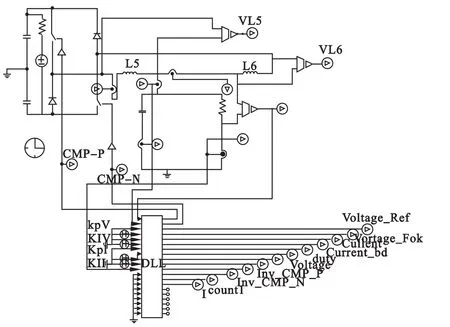
圖3 基于雙Buck逆變拓撲的PSIM仿真圖

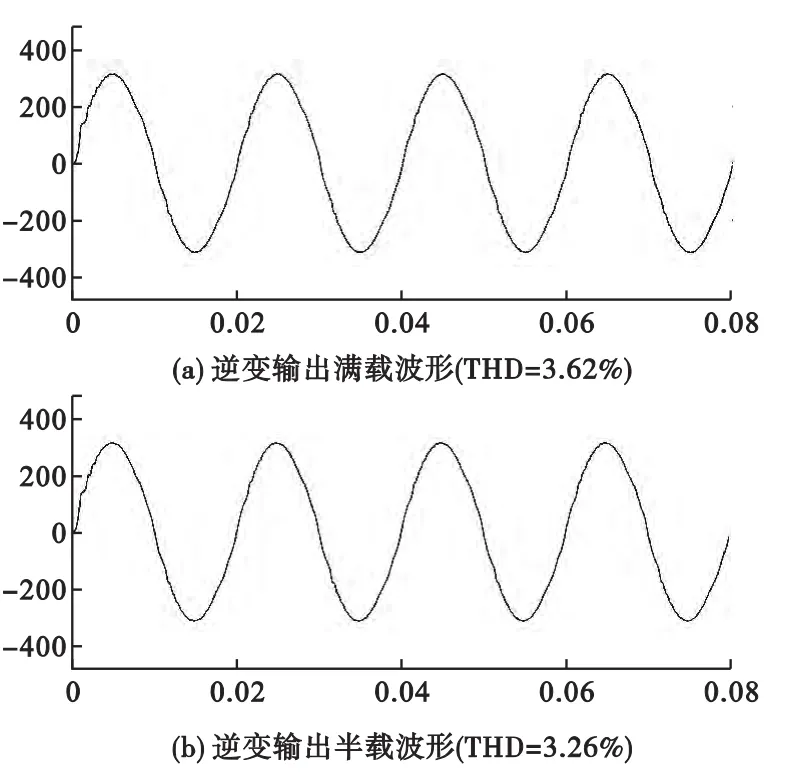
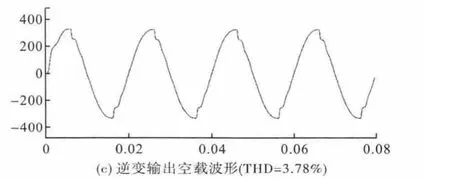
圖4

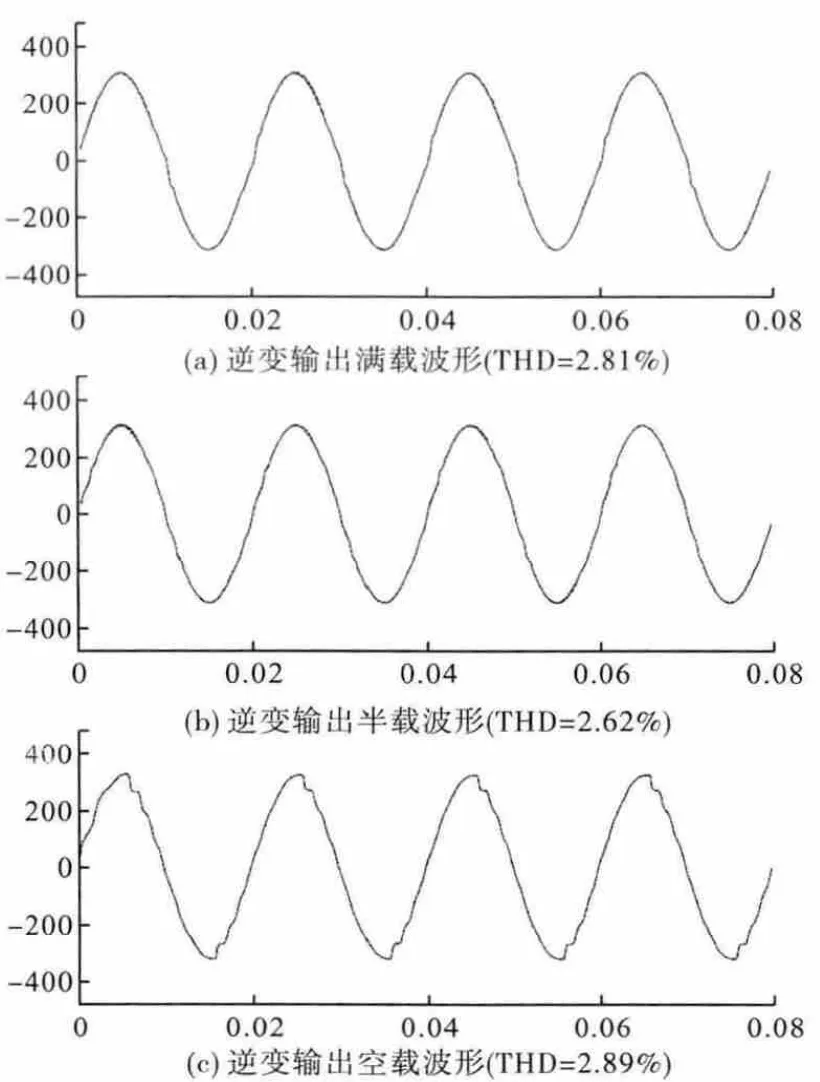
圖5

圖4是外環PI控制，內環P控制產生的輸出電壓波形圖，圖5是外環PI控制，內環單周期控制的輸出電壓波形圖，從上面的仿真波形分析看出，負載分別對滿載、半載、空載的時候，當內環采用基于預測電流法的單周期控制的時候比內環采用比例調節控制的輸出電壓波形畸變率有了很大的改善。

5 結論

本文研究的雙Buck逆變器，從拓撲結構上看，結構較為簡單，由于開關管和續流二極管可以分別優化設計，具有損耗小、效率高的特點，同時由于不需要設置死區時間，輸出波形畸變率較低。由于整個控制系統采用的是數字化控制，比模擬控制電路的元器件少了很多，簡化了控制電路的設計。數字控制采用雙環控制，內環采用了基于預測電流法的單周期控制算法，進一步降低了輸出電壓波形畸變率。

［1］張先進，龔春英.一種SPWM控制雙Buck半橋逆變器研究［J］.電氣傳動，2009，39(2):48－51.

［2］洪峰，劉軍.滯環電流控制型雙BUCK逆變器［J］.電工技術學報，2004，19(8):73－77.

［3］陳堅.電力電子學—電力電子變換和控制技術［M］.北京:高等教育出版社，2004.

［4］Zargari N R.Two Switch High Performance Current Regulated DC/AC Converter Module［J］.IEEE Transactions on Industry Applications，1995，31:583－589.

［5］Gerald R Stanley，Kenneth M Bradshaw.Precision DC to AC Power Conversion by Optimization of the Output Current Waveform the Half Bridge Revisited［J］.IEEE Transactions on Power Electronics，1999，14(2):272－280.

［6］萬珍梅，馬運東.單周期控制正負輸出Boost PFC的研究［J］.電力電子技術，2008，42(9):12－14.