平面彈性問題的有限元程序設計
任國彪,馮美祿
(1.鄭州大學數學與統計學院,鄭州 450052;2.河南省教育技術裝備管理中心,鄭州 450001)
1 引言
平面彈性問題是工程上經常遇到的問題,用有限元方法解決平面彈性問題具有計算精度高、方法規則簡單的特點。但相對于一般的二階問題和四階問題標量求解不同,平面問題要求的是一個向量解,另外在解和Locking上也有不同的限制。因此,平面彈性問題求解時比較復雜,作者根據求解該問題時遇到的情況以及相關的一些思路做出闡述。
有限元法發展到今天,已成為工程數值分析的有力工具。特別是在固體力學和結構分析領域內,有限元法取得了巨大的進展,利用它已成功地解決了一大批有重大意義的問題,很多通用程序和專用程序投入了實際應用。同時,有限元法又是仍在快速發展的一個學科領域,它的理論,特別是應用方面的文獻經常且大量地出現在各種刊物和文集當中。三十多年來,有限元法的應用已由彈性力學平面問題擴展到空間問題、板殼問題;由靜力平衡問題擴展到穩定問題、動力問題和波動問題。分析的對象從彈性材料擴展到塑性、粘彈性、粘塑性和復合材料等;從固體力學擴展到流體力學、傳熱學等連續介質力學領域。在工程分析中的作用已從分析和校核擴展到優化設計并和計算機輔助設計技術相結合。可以預計,隨著現代力學、計算數學和計算機科學技術等學科的發展,有限元法作為一個具有鞏固理論基礎和廣泛應用效力的數值分析工具,必將在國民經濟建設和科學技術發展中發揮更大的作用,其自身亦將得到進一步的發展和完善。
有限元法是現代工程設計和科學計算的重要數值方法之一。利用計算機有限元軟件對工程問題進行數值計算和分析已成為有限元法中一個必不可少的環節。
2 平面彈性問題的模型

2.1 下面考慮純位移的平面彈性問題:
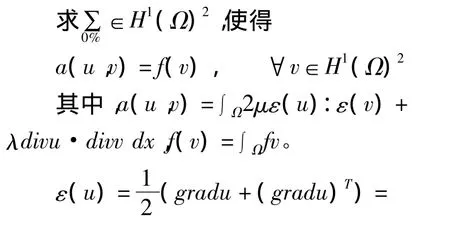

2.2 離散方程
設平面彈性有限元(K,PK,∑K),單元自由度數為en,總體自由度數為MP,有限元空間為Vh,由有限元導出的插值函數為:

2.3 求標準基函數
對于自由度較少的單元,可以直接求解其標準基函數,對于自由度比較復雜的單元,如采用邊積分值、外法向導數值、單元積分值,標準基函數比較復雜,手工很難求出。其實,在有限元計算中,標準基函數不必顯式給出,下面給出一種求基函數的方法。
設有限元的形函數空間為PK=span{φi;1≤i≤n},兩個分量的自由度分別為Di、Ei,將自由度表示為形函數的組合:
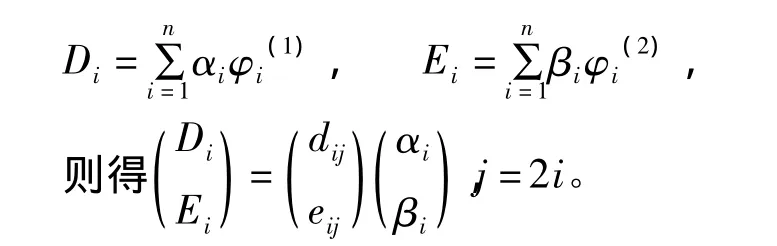

3 有限元算法與編程
3.1 單元編號和單元節點編號
單元編號和單元節點編號的原則是方便未知量求解,以及求解向量的使用。
單元節點編號的方法:
因為平面彈性問題是一個向量問題,因此在單元編號上和普通有限元方法單元節點編號是不同的。一般來說,按逆時針編號(順時針也可以),按自由度組先第一分量、后第二分量編號,一個接一個自由度組連續編號。
(gij)en×en,1 ≤ i≤ ES,1 ≤ j≤ en。
下面是以CR元例,說明單元編號和單元節點編號,CR元的共有3組6個自由度,分別是三邊ei的中點,如圖1所示。
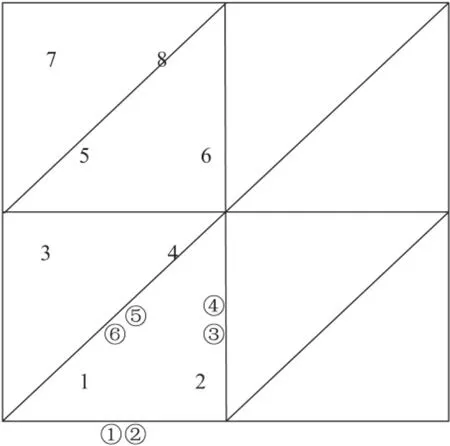
圖1 單元和單元節點編號
3.2 單剛矩陣的形成:
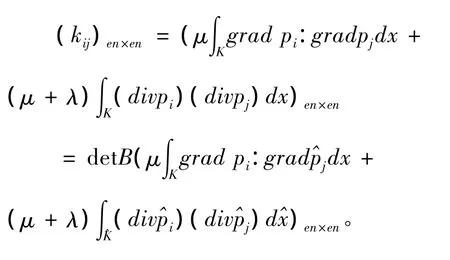
3.3 荷載向量的形成:
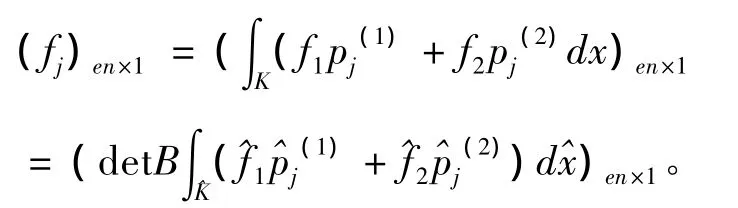
3.4 合成總剛矩陣:
設第m個單元的單剛矩陣AKj=(kij)en×en,它的總體單元節點編號是 m1,m2,L,men,那么它在總剛中的位置是:

3.5 合成總體載荷向量:
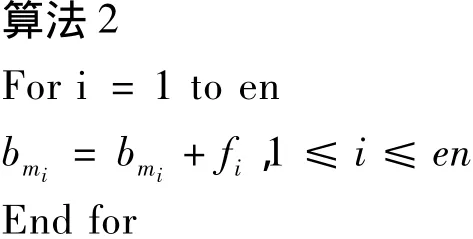
3.6 支撐條件
在形成總體剛度矩陣時還需要加入支撐條件,這里僅以固支條件為例給予說明。傳統的方法是將總剛矩陣A的主對角線元素aij置為很大的一個數,如10308,這種滿足支撐條件的方法會使得A的條件數變大,不利于迭代求解。事實上,只須將主對角線元素aii置為1,第i行、第i列其它元素置為0,對應的荷載列陣第i行的元素也置為0。這種支撐條件的優點是可以使A的條件數大大變小,因而有利于迭代法求解。

方程組求解,方法很多,有分解法、迭代法、共軛梯法等。
4 誤差估計
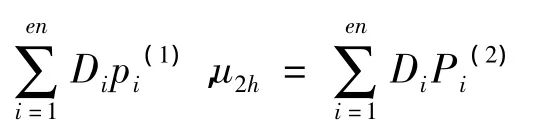


5 算例
算例1:考慮下面純位移的齊次平面彈性問題:
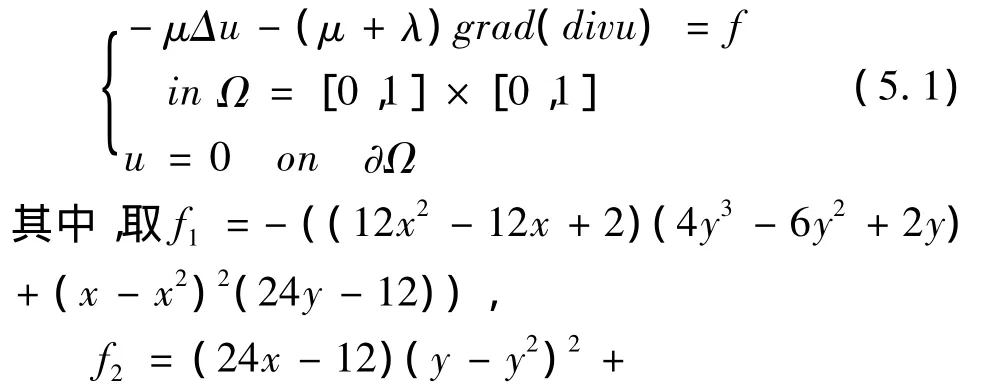

單元采用正則均勻剖分,在μ,λ不同取值下的0模、0模誤差和1半模誤差的計算結果分別見表一、表二和表三。
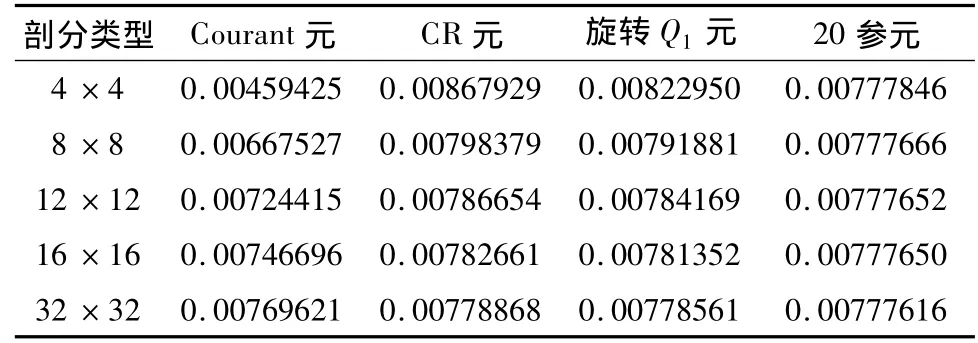
表一 解的0模(μ=λ=1)
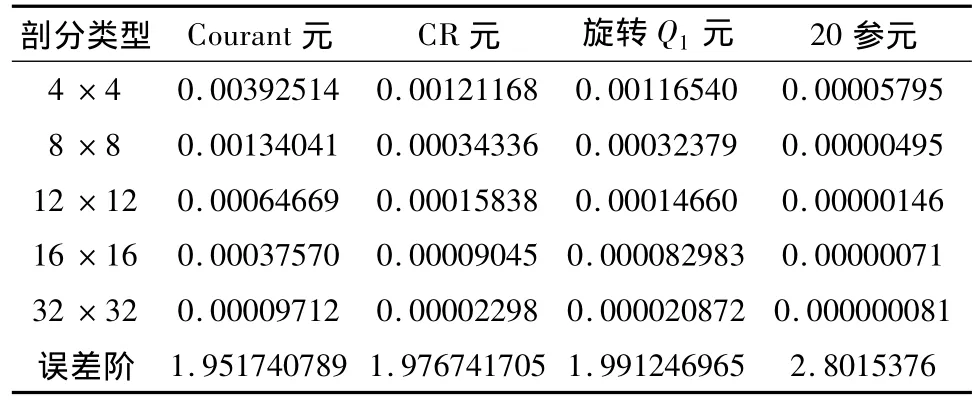
表二 計算精度(0模誤差)表(μ=λ=1)
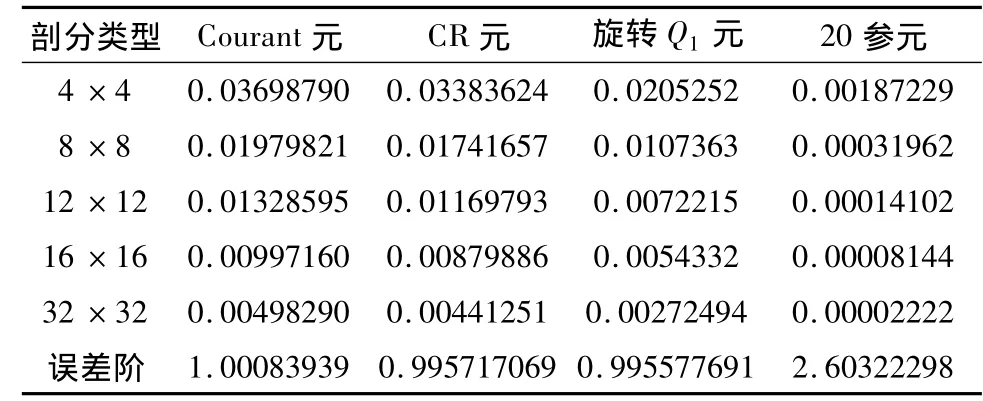
表三 計算精度(1模誤差)表(μ=λ=100000)
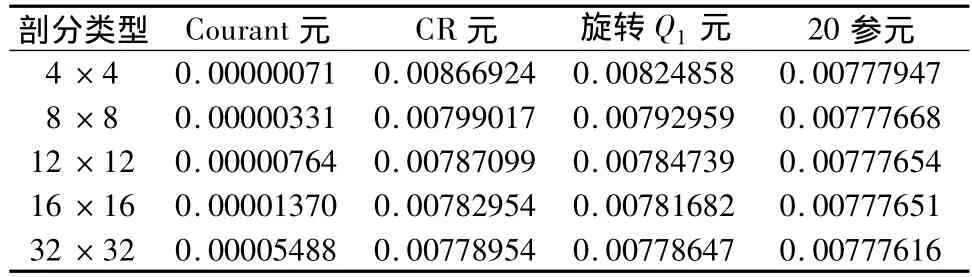
表四 解的0模μ=λ=1)
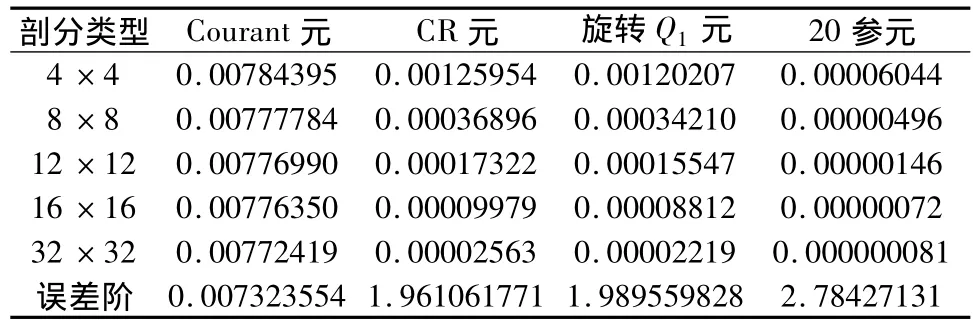
表五 計算精度(0模誤差)表(μ=1,λ=100000)
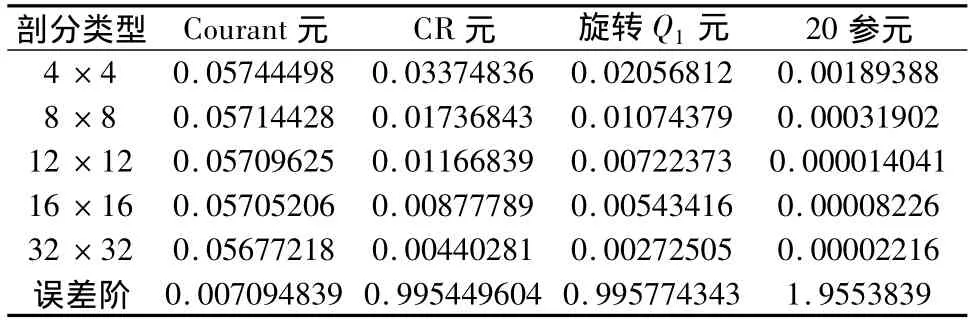
表六 計算精度(1模誤差)表(μ=1,λ=100000)
從表四、表五、表六的數值結果我們可以看出:有限元方法在求解平面彈性問題的有效性。
[1]李開泰,黃艾香,黃慶懷.有限元法及其應用[M].北京:科學出版社,2006.
[2]劉爾烈,崔恩第,徐振鐸.有限單元法及程序設計[M].天津:天津大學出版社,2002.
[3]王勖成,邵敏.有限單元法基本原理和數值方法[M].北京:清華大學出版社,1997.

