新型雙活塞磁流變阻尼器的理論分析與實驗研究

王 強，陳照波，Ahmadian Mehdi，劉文濤

（1.哈爾濱工業大學機電工程學院，哈爾濱 150001；2.弗吉尼亞理工大學機械工程系，黑堡VA24061，美國）

新型雙活塞磁流變阻尼器的理論分析與實驗研究

王 強1，陳照波1，Ahmadian Mehdi2，劉文濤1

（1.哈爾濱工業大學機電工程學院，哈爾濱 150001；2.弗吉尼亞理工大學機械工程系，黑堡VA24061，美國）

針對空間柔性桁架結構振動半主動控制的需要，提出了一種重量輕、結構緊湊的雙活塞磁流變阻尼器。基于磁流變液流變特性和流體動力學理論，通過分析阻尼器節流通道內的流場情況，建立了阻尼力與活塞速度之間的關系。給出了適用于阻尼器初始設計的簡化阻尼力計算方法，準靜態測試的結果驗證了計算方法的正確性。針對動態測試實驗結果中輸出力在去程和回程的不對稱問題，提出了一種改進的非對稱雙曲正切模型。結果表明，改進模型能夠準確描述新型阻尼器的動力學特性，在去程和回程都有很高的建模精度。

磁流變阻尼器；磁流變液；Bingham模型；非對稱雙曲正切模型

根據結構型式和所使用磁流變液的工作模式，現有磁流變阻尼器可以歸納為如圖1所示的四種基本構型：雙出桿剪切閥式［1］，單出桿剪切閥式［2］，單出桿流動式［3］和旁路流動式［4］，其他的磁流變阻尼器絕大多數可以認為是上述四種基本構型的變種［5］。例如，車輛工程中常用的雙筒型磁流變阻尼器［6］，可以認為是在單出桿流動式的基礎上，將蓄能器置于內筒和外筒之間而得到的一種變體。四種基本構型中最常用的是雙出桿剪切閥式和單出桿流動式。現有磁流變阻尼器的共同特點是可以輸出很大的阻尼力，同時有較大的行程，一般用于大型建筑、土木結構以及機械設備的振動半主動控制。但是針對空間微重力環境下的輕質柔性桁架結構［7］，其振動半主動控制對阻尼器的輸出力大小要求不高，但是對阻尼器的重量和結構尺寸有嚴格要求的情況下，現有的磁流變阻尼器由于重量和尺寸過大而不再適用。

為了滿足重量輕和結構緊湊的要求，本文提出一種新型結構的磁流變阻尼器。在對節流通道內的磁流變液進行流體力學分析的基礎上，給出阻尼力的計算公式。通過實驗方法對自制新型阻尼器進行測試，驗證阻尼力計算公式，并獲得阻尼器的非線性滯后特性曲線。基于實驗曲線，建立適用于新型阻尼器動態分析與控制的動力學模型。

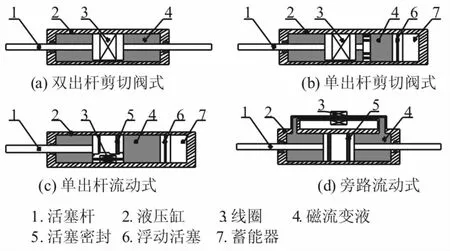
圖1 磁流變阻尼器的四種基本構型Fig.1 Four MR damper basic configurations

1 新型雙活塞磁流變阻尼器

提出的新型雙活塞磁流變阻尼器［8］的結構如圖2所示，阻尼器有左、右兩個動密封活塞，與外套管之間采用O型圈動密封；線圈活塞用于連接兩個動密封活塞；線圈纏繞在線圈活塞上，引線通過左側活塞引出；外套管和活塞桿分別與被控結構相連。當活塞桿與外套管之間相對運動時，磁流變液被迫通過環形節流通道在左、右腔室之間交換流動，在線圈產生的磁場作用下產生可控阻尼力。磁流變液工作在包含流動模式和直接剪切模式的混合模式下，也稱為剪切閥式。

圖2 新型雙活塞磁流變阻尼器結構圖Fig.2 Schematic of the double-piston MR damper

除了內套管和線圈活塞需要采用導磁材料制造外，其他零件可以選用高強度、輕質非磁性材料制造，以最大限度降低阻尼器自身重量。外套管和內套管之間為過盈配合，裝配采用熱裝法完成，這樣可以減少零件數量，壓縮阻尼器徑向尺寸。所有零件都被置于外套管內，阻尼器外形規則，有利于在被控結構中的布置。與現有阻尼器相比，新型雙活塞磁流變阻尼器特別適于空間微重力環境下輕質柔性桁架結構振動半主動控制。

2 穩態流體動力學分析

2.1 節流通道內的磁流變液

在圖1所示的雙出桿剪切閥式［1］和單出桿剪切閥式［2］磁流變阻尼器中，磁流變液流動方向與活塞運動方向相反，穩態流體動力學分析時速度邊界條件的一側為活塞速度v0，另一側為0，如圖3（a）所示；在單出桿流動式［3］磁流變阻尼器中，磁流變液流動方向和運動方向也是相反的，速度邊界條件兩側對稱，同為活塞速度v0，如圖3（b）所示；而在旁路流動式［4］磁流變阻尼器中無相對運動，速度邊界條件兩側同為0，如圖3 （c）所示；而新型阻尼器中，節流通道內磁流變液的流動方向與活塞運動速度方向相同，速度邊界條件如圖3 （d）所示。其中，第四類速度邊界條件是新型阻尼器所特有的，尚沒有相關文獻對其進行分析。速度邊界條件的不同會造成節流通道內流速分布的不同，最終影響阻尼力。因此，首先需要對新型阻尼器節流通道內的流速和剪切應力的分布進行分析。

圖3 磁流變阻尼器的四類速度邊界條件Fig.3 Four types velocity boundary conditions

在外加磁場作用下，磁流變液的流動特性可用Bingham塑性模型表達

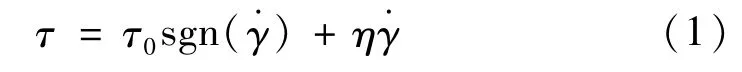
式中，τ為磁流變液的剪切應力；τ0為剪切屈服應力，與磁場強度有關為剪切應變率；η為磁流變液零磁場粘度。

由于活塞直徑遠大于節流通道間隙，可以使用平板模型對磁流變液流速和剪切應力進行分析。如圖4所示，平板間隙h＝R2－R1，平板寬度w＝π（R1+R2）。其中，R1為線圈活塞外半徑，R2內套管內半徑。

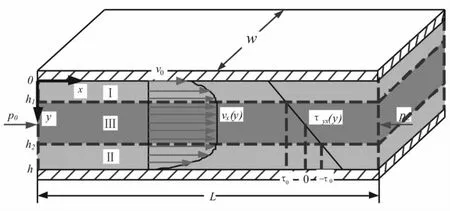
圖4 平板間的流速和剪切應力分布Fig.4 Stress and velocity profiles through the parallel duct

假設磁流變液在壓差下做一維層流流動，忽略慣性力和體積力，流體基本力學方程Navier-Stokes的x方向項簡化為：

2.2 壓力梯度與活塞速度的關系

將τyx（h1）＝τ0和τyx（h2）＝－τ0代入式（3）可以求出積分常數C1：

根據速度邊界條件vⅠ（h1）＝vⅡ（h2），綜合式（6）和式（9），并將式（11）代入，可得：

2.3 無量綱化與阻尼力計算公式

在阻尼器的初始設計階段，為了簡化計算，定義無量綱速度V，無量綱壓力梯度P，無量綱屈服強度T分別為：

注意到，此處無量綱速度V的符號與文獻［1］中的相反。

式（20）可以通過數值方法求解。在實用的磁流變阻尼器設計參數的范圍內［1］，無量綱參數之間的關系可以用下式近似表示：

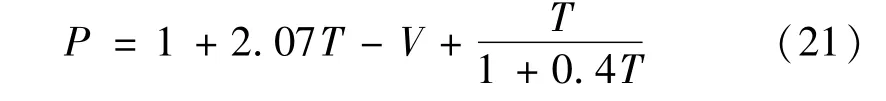
阻尼力可以由下式求得：

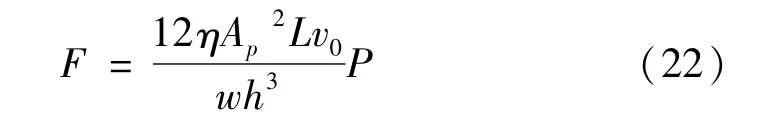
3 自制新型阻尼器及其測試

3.1 自制新型阻尼器

基于提出的新型雙活塞結構，制作完成的磁流變阻尼器重量為82 g（充液后），外徑為16 mm，行程為15 mm。其他主要參數：線圈活塞外徑為12.22 mm，內套管內徑為12.58 mm，外套管內徑為14.22 mm，有效節流長度L為10.16mm。線圈長度為10.16 mm，線徑為0.321 mm，匝數為110，電阻為1.1Ω。所使用的磁流變液來自美國Lord公司，型號為MRF－122EG。組裝前和完成組裝的新型雙活塞磁流變阻尼器如圖5所示。

圖5 自制新型雙活塞磁流變阻尼器Fig.5 The double-piston MR damper prototype

3.2 實驗裝置

磁流變阻尼器具有強非線性特性，理論計算不能完全準確地獲得其實際工作性能，需要采用實驗方法對其進行研究。實驗測試分為準靜態測試和動態測試。準靜態測試可以獲得阻尼器輸出力與活塞速度之間的關系曲線。動態測試可以獲得輸出力－位移和輸出力－速度曲線。測試所采用的實驗裝置見圖6，新型阻尼器通過夾具安裝在阻尼器試驗機上，試驗機使用電磁驅動器對阻尼器進行激勵，固定在橫梁和阻尼器之間的力傳感器測量力信號，通過直流電源對阻尼器進行供電。數據采集系統可以對試驗機進行控制，并對獲取的實驗數據進行處理。

圖6 新型阻尼器實驗裝置圖Fig.6 Experimental setup for the prototype damper

3.3 準靜態測試

準靜態測試過程中，使用正弦信號進行激勵，采集活塞通過平衡點時，最大速度和對應的阻尼力。通過改變激勵頻率和幅值來改變最大速度，五次循環取平均值作為測試值。改變驅動電流，就可以測得阻尼器在不同驅動電流下，一定速度范圍內的輸出力－速度曲線。這組曲線可以反映阻尼器輸出力的大小和隨速度的變化趨勢，可以用于阻尼力計算公式的驗證。

測得的輸出力主要包含磁流變液流過節流通道產生的阻尼力和動密封產生的摩擦力兩部分。在完成阻尼器輸出力測試后，將其中的磁流變液倒出，采用與輸出力測試相同的方法，對阻尼器的摩擦力進行測試。將相同活塞速度下輸出力值減去摩擦力值就可以得到阻尼力的實測值。最終得到的實測輸出力和摩擦力與活塞速度之間的關系曲線如圖7所示。

相同驅動電流時，輸出力隨活塞速度的增大而增大，這反映的是節流通道內磁流變液的黏性阻尼特性；相同活塞速度時，輸出力隨驅動電流的增大而增大，這反映的是磁流變液屈服強度隨磁場變化的塑性特性。摩擦力隨速度有下降趨勢，而且速度逐漸減緩。

3.4 阻尼力計算公式的驗證

節流通道內磁場強度除了跟驅動電流有關外，還跟阻尼器結構和線圈參數以及磁流變液的磁化曲線等許多參數有關。本研究中首先借助磁場有限元分析軟件FEMM求出特定驅動電流I下節流通道內磁場強度H。再根據圖8中所示的磁流變液磁場強度H與剪切屈服應力τ0之間的實驗特性曲線得到對應的剪切屈服強度τ0。表1為不同驅動電流I下，磁場強度值H和對應的剪切屈服應力τ0的值。

根據阻尼器的結構參數和磁流變液參數，由式（21）和式（22）就可以求出特定驅動電流下，不同活塞速度對應的阻尼力。圖9為不同驅動電流下，準靜態條件下實測阻尼力與計算阻尼力曲線。可以看出，通過前述阻尼力計算公式可以較為準確地計算出新型阻尼器在不同驅動電流和活塞速度下的阻尼力。

圖7 準靜態測試條件下實測輸出力和摩擦力與速度的關系Fig.7 Measured output and friction force versus piston velocity

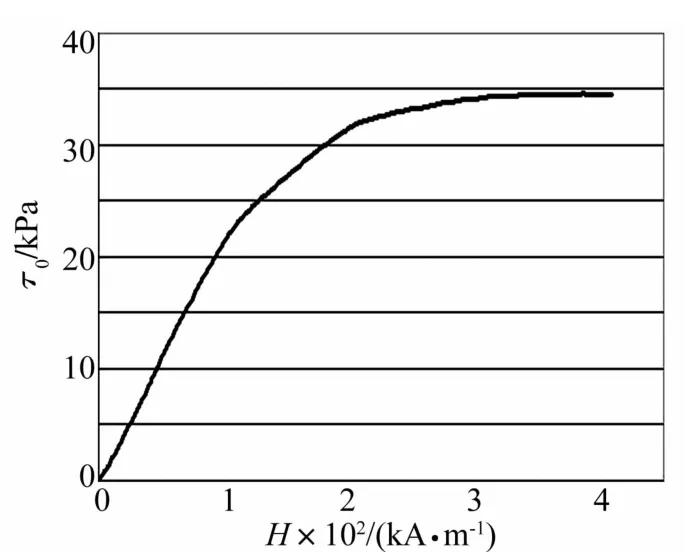
圖8 MRF－122EG磁流變液磁場強度H與剪切屈服應力τ0之間的實驗特性曲線Fig.8 Tested H versusτ0curve for MRF－122EG

圖9 準靜態測試條件下阻尼力實測值與計算值的比較Fig.9 Measured and calculated damping force

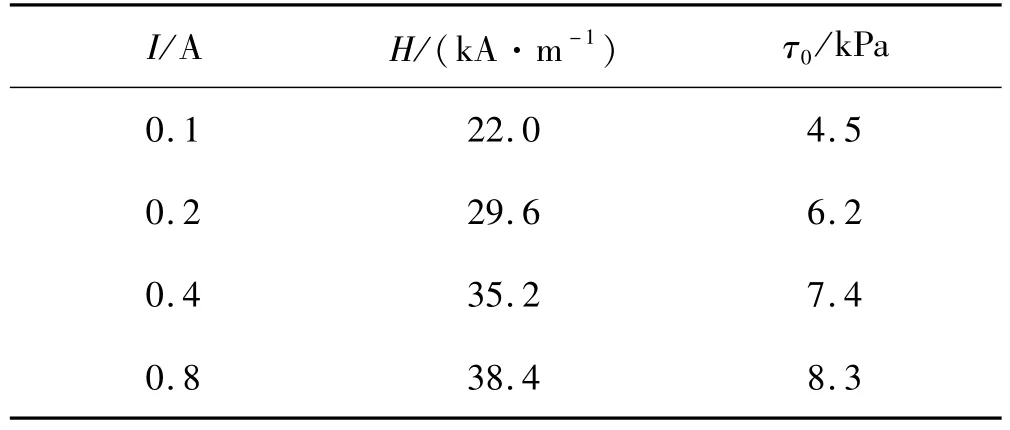
表1 不同驅動電流I下磁場強度H與剪切屈服應力τ0值Tab.1 Calculated H andτ0under different I

同時注意到，在不同的驅動電流下，實測阻尼力－速度曲線的斜率都要大于對應的計算值曲線。分析后認為，這主要是因為摩擦力的測試條件與阻尼器實際工作條件有差異，O型圈處于不同的工作狀態所導致的。O型圈在溝槽中受磁流變液壓力作用下產生變形，被擠向間隙位置，達到密封效果。當活塞運動速度增大時，磁流變液產生的壓力隨之增大，迫使O型圈發生更大的變形，獲得更緊的密封，而這會導致更大的摩擦力。摩擦力測試時，由于只保留少量磁流變液作為O型圈與外套管內壁之間的潤滑劑，因此沒有上面描述的摩擦力隨活塞速度增大而增大的現象，反而出現了下降的趨勢，如圖7所示。也就是說，實測摩擦力要小于正常工作時的摩擦力，而且活塞速度越大，差值越大，反映在阻尼力－速度曲線上就是實測阻尼力曲線的斜率要稍大于理論計算值曲線。

3.5 動態測試

前述阻尼力計算公式和準靜態測試結果，不能反映磁流變阻尼器的動力學特性，尤其是明顯的輸出力－速度滯后特性。因此，需要對自制阻尼器進行動態測試，以獲得阻尼器的動力學特性曲線，為后續阻尼器動力學建模與控制提供條件。

測試時同樣使用正弦信號作為激勵，記錄阻尼器去程和回程整個循環內的活塞位移、速度和對應的輸出力。取不同的激勵幅值和頻率組合，改變驅動電流，就可以得到不同激勵條件和驅動電流下的阻尼器輸出力－位移和輸出力－速度特性曲線。

4 新型阻尼器的非對稱建模

4.1 非對稱雙曲正切模型

圖10中動態測試結果表明，新型阻尼器具有典型的磁流變阻尼器的動力學特性。其輸出力－速度曲線存在明顯的兩個區域：屈服前區和屈服后區；其中在屈服前區存在明顯的滯后，并且滯環的大小隨驅動電流增大而增大；在屈服后區存在明顯的局部滯環。與現有磁流變阻尼器不同的是，新型阻尼器的輸出力在去程和回程有明顯的差異，尤其是在屈服后區，輸出力－速度曲線的斜率明顯不同，并且去程存在明顯的局部滯環，而回程則不明顯，而且隨著驅動電流的增大，不對稱性有增大的趨勢。一般的磁流變阻尼器參數化模型在一個周期內的輸出力是對稱的［9－10］，也就是假設阻尼器在去程和回程具有相同的特性。Kwok等［11］，探討了一種基于Bouc-Wen模型的速度滯回曲線不對稱修正方法，引入了一個修正參數，對速度進行修正，其針對的區域是屈服前區和屈服后區轉換點附近。Wang等［12］提出了一種不對稱阻尼力產生算法，實現了不對稱速度滯回曲線的建模，其中不對稱性主要體現在屈服前區滯回曲線的高度和位置。而本研究中新型阻尼器的不對稱性主要表現在屈服后區，包含速度滯回曲線的斜率和局部滯環兩方面問題。因此，提出一種新的參數化模型來實現新型阻尼器的精確建模。

磁流變阻尼器的雙曲正切模型，不但能夠準確描述阻尼器屈服前區和屈服后區特性，而且形式簡單、計算效率高，同時模型參數與實驗曲線有較為明確的對應關系［13－14］。在一定條件下，其建模精度可以高于Bouc-Wen，修正的Bouc-Wen，修正的Dahl和修正的LuGre等模型［14］。基于雙曲正切模型，本文提出一種改進的非對稱雙曲正切模型，實現對阻尼器的去程和回程輸出力分別進行建模，模型的表達式為：

式中，c，c′分別為黏性系數和其修正系數，它們的作用是調整屈服后區速度滯回曲線的斜率；k、k′分別為彈性系數和其修正系數，用于調整屈服后區的局部滯環；α為滯環的尺寸系數，β和δ為滯環形狀系數，保證去程和回程有相同的滯環高度、斜率和寬度；f0、f′0分別為輸出力補償系數和其修正系數。

為了保證曲線在去程和回程連接處的平滑過渡，三個修正系數之間需要滿足以下條件：

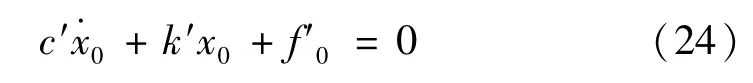
4.2 模型參數辨識

首先使用整個周期內的實驗數據對雙曲正切模型進行參數辨識，獲得的參數值作為改進模型參數辨識的初始值，提高計算的效率。根據阻尼器動態測試數據，使用非線性最小二乘法辨識出的模型參數見表2。

4.3 建模結果討論

對應不同的驅動電流，使用辨識后的非對稱雙曲正切模型和實測速度、位移值計算出的輸出力和實測輸出力的對比見圖10。

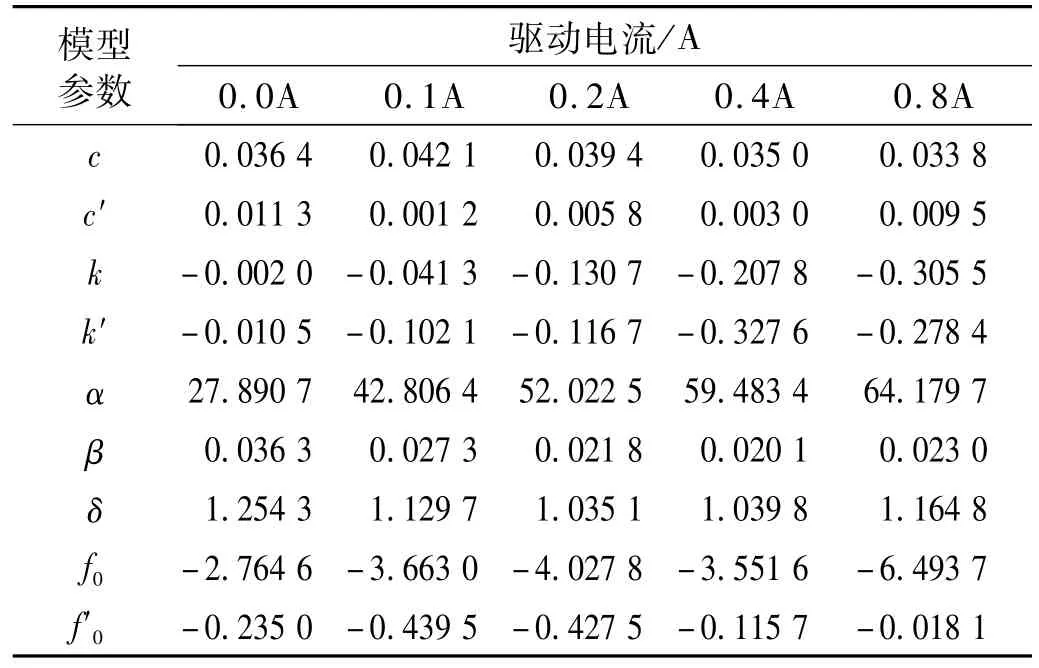
表2 非對稱雙曲正切模型辨識參數Tab.2 Identified asymmetric model parameters

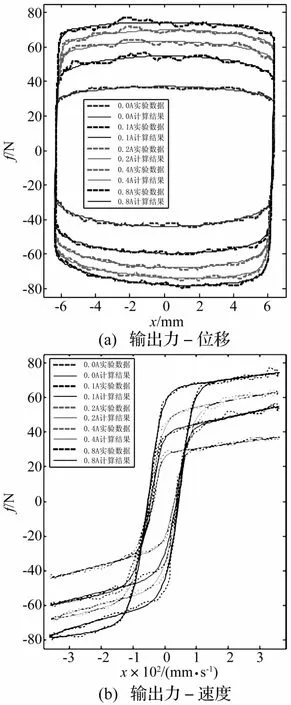
圖10 動態測試條件下實驗數據與模型計算結果對比Fig.10 Comparison ofmeasured and reconstructed curves under dynamical testing condition

以驅動電流為0.8 A時的輸出力－速度曲線為例，由圖可以明顯看出，實驗數據在去程和回程存在明顯不同，去程實驗曲線在屈服后區存在明顯的局部滯環，而在回程則沒有，屈服后區曲線的斜率也明顯不同。不管采用何種對稱模型，均相當于在去程和回程曲線之間的折衷，這會造成整個周期內建模的不準確。而采用非對稱雙曲正切模型就可以同時兼顧去程和回程特性。

由圖10（a）和（b）可以看出，模型計算結果不僅準確描述了屈服前區和屈服后區的實驗數據曲線，而且對去程實驗數據曲線存在的局部滯環，以及屈服前、后區轉換處曲線交叉點的位置描述同樣十分精確。

5 結 論

為了滿足空間柔性桁架結構振動半主動控制對作動器的需要，提出了一種雙活塞磁流變阻尼器。基于平板模型假設，建立了阻尼力與活塞速度、阻尼器結構參數和磁流變液參數之間的關系，給出了阻尼力計算方法。設計實驗完成了自制新型阻尼器的準靜態和動態測試。提出了一種非對稱模型描述阻尼器的非線性動力學特性。

（1）基于新型雙活塞結構的自制磁流變阻尼器重量僅82 g，外徑16 mm，電流0.8 A時，阻尼力最大可達80 N。在保證了阻尼器重量輕和結構緊湊的前提下，阻尼力達到了空間桁架結構振動控制的要求。

（2）自制新型阻尼器的準靜態測試結果驗證了阻尼力計算方法的正確性。

（3）提出的非對稱雙曲正切模型可以準確描述阻尼器動力學特性，同時提高了阻尼器輸出力在去程和回程的建模精度。

［1］Yang G，Spencer B F，Carlson JD，et al.Large-scale MR fluid dampers：Modeling and dynamic performance considerations［J］.Engineering Structures，2002，24（3）：309－323.

［2］Hu H S，Jiang X Z，Wang J，et al.Design，modeling，and controlling of a large-scalemagnetorheological shock absorber under high impact load［J］.Journal of Intelligent Material Systems and Structures，2012，23（6）：635－645.

［3］Dyke S J，Spencer B F，Sain M K，et al.Modeling and control of magnetorheological dampers for seismic response reduction［J］.Smart Materials＆Structures，1996，5（5）：565－575.

［4］Cook E，Hu W，Wereley N M.Magnetorheological bypass damper exploiting flow through a porous channel［J］.Journal of Intelligent Material Systems and Structures，2007，18 （12）：1197－1203.

［5］Zhu X C，Jing X J，Cheng L.Magnetorheological fluid dampers：A review on structure design and analysis［J］.Journal of Intelligent Material Systems and Structures，2012，23（8）：839－873.

［6］石秀東，錢林方，徐亞棟.雙筒磁流變阻尼器動力學特性研究［J］.振動與沖擊，2007，（10）：41－44.

SHI Xiu-dong，QIAN Lin-fang，XU Ya-dong.Study on dynamic characteristics of a twin tube magneto-rheological damper［J］.Journal of Vibration and Shock，2007，（10）：41－44.

［7］Huo L S，Song G B，Nagarajaiah S，et al.Semi-active vibration suppression of a space truss structure using a fault tolerant controller［J］.Journal of Vibration and Control，2012，18（10）：1436－1453.

［8］陳照波，邁迪·阿馬迪安，王強，等.增加動態輸出力可調范圍的緊湊型輕量化的磁流變阻尼器［P］.中國，發明專利，201110420869.8，2013.12.25.

［9］Wang D H，Liao W H.Magnetorheological fluid dampers：A review of parametric modelling［J］.Smart Materials＆Structures，2011，20（2）：023001－023034.

［10］鄧志黨，高峰，劉獻棟，等.磁流變阻尼器力學模型的研究現狀［J］.振動與沖擊，2006，25（3）：121－126.

DENG Zhi-dang，GAO Feng，LIU Xian-dong，etal.State-ofart research on dynamical，models of magnetorheological damper［J］.Journal of Vibration and Shock，2006，25（3）：121－126.

［11］Kwok N M，Ha Q P，Nguyen M T，et al.Bouc-wen model parameter identification for a MR fluid damper using computationally efficient ga［J］.Isa Transactions，2007，46（2）：167－179.

［12］Wang E R，Wang W J，Wang H，et al.Describing asymmetric hysteretic F-V characteristics of a MR damper resulted form symmetric MR damper［J］.Journal of Nanjing Normal University（Engineering and Technology Edition），2008，8（1）：1－6.

［13］Kwok N M，Ha Q P，Nguyen TH，et al.A novel hysteretic model for magnetorheological fluid dampers and parameter identification using particle swarm optimization［J］.Sensors and Actuators a-Physical，2006，132（2）：441－451.

［14］Sahin I，Engin T，Cesmeci S.Comparison of some existing parametricmodels formagnetorheological fluid dampers［J］.Smart Materials＆Structures，2010，19（3）：035012－035022.

Analysis and tests for a novel double-piston MR damper

（1.School of Mechatronic Engineering，Harbin Institute of Technology，Harbin 150001，China；2.Department of Mechanical Engineering，Virginia Polytechnic Institute and State University，Blacksburg VA24061，USA）

Here，a novel double-piston magnetorheological（MR）damper was proposed，its lightweight and compact size featuresmade it especially suit for lightweight space flexible truss structures'vibration semi-active control.The fluid dynamic analysis of the damper was conducted using Bingham plastic model and the fluid dynamics theory.Based on a proper hypothesis，a simplified damping force calculation method fit for preliminary design phase was proposed.Testswere designed and performed to obtain the damper's hysteretic behavior under different drive currents.Aiming at the damper tests'output force asymmetry problem at go stroke and return-one，an improved asymmetric hyperbolic tangentmodelwas presented.Comparative study results showed that the improved model can describe precisely the dynamic hysteretic behavior of this double-piston MR damper under different drive currents；it has a highermodeling accuracy at go-stroke and return-one simultaneously.

magnetorheological（MR）damper；magnetorheological fluid；Bingham model；asymmetric hyperbolic tangentmodel

TB383；O373

A

10.13465／j.cnki.jvs.2015.21.025

國家自然科學基金資助項目（10972065；11372083）

2014－07－04 修改稿收到日期：2014－10－11

王強男，博士生，1985年2月生

陳照波男，博士，教授，1967年4月生

WANGQiang1，CHEN Zhao-bo1，AHMADIAN M2，LIUWen-tao1