蜂窩夾層復合材料不確定性參數識別方法

姜東，吳邵慶，費慶國，韓曉林

(1.東南大學工程力學系，南京 210096;2.江蘇省工程力學分析重點實驗室，南京 210096)

蜂窩夾層復合材料不確定性參數識別方法

姜東1，2，吳邵慶1，2，費慶國1，2，韓曉林1，2

(1.東南大學工程力學系，南京 210096;2.江蘇省工程力學分析重點實驗室，南京 210096)

提出蜂窩夾層復合材料不確定性參數識別方法。采用三明治夾芯板理論建立鋁蜂窩夾層結構的初始有限元模型，其中芯層等效彈性參數由均勻化方法計算。據芯層結構及相對靈敏度分析，選存在不確定性且對動態特性敏感性較大的面外剪切模量及面板厚度為待識別參數。對6塊鋁蜂窩復合材料板進行自由－自由邊界條件下動態試驗，獲得試驗模態參數的均值及標準差。據試驗結果采用所提方法識別鋁蜂窩夾層板不確定性參數。結果表明，對存在不確定性參數的鋁蜂窩夾層復合材料用該方法能準確識別參數的均值及標準差，并建立具有準確統計意義的動力學模型。

蜂窩夾層復合材料;不確定性;有限元;參數識別

蜂窩夾層復合材料因結構形式獨特及諸多單質材料不具備的優異性能，已成為航空航天結構中不可或缺的材料之一［1］。然而，由于制備工藝造成的面板參數及胞孔排列不規則、孔壁材料分布不均勻、填充材料孔洞等導致蜂窩夾層復合材料力學性能存在明顯不確定性。

蜂窩夾層復合材料力學性能研究建立在對芯層等效彈性參數研究基礎上［1－6］。用等效彈性參數建立有限元模型能較大程度提高分析效率。Gibson等［1］考慮蜂窩芯層軸向、剪切變形推導出正交各向異性的9個彈性參數;富明慧等［2］考慮蜂窩壁板伸縮變形對面內剛度影響，提出考慮蜂窩芯層面內剛度的簡化方案，并對面內等效彈性參數的Gibson計算公式進行修正。陳玳珩等［3］提出滿足蜂窩芯與面板間位移連續條件的等效彈性參數分析方法;徐勝今等［4］基于低階剪切理論提出正交各向異性蜂窩夾層板高精度等效分析方法;張鐵亮等［5］通過對三種不同等效方法的靜、動力計算結果比較研究，認為三明治夾芯板理論為等效參數的優選方法。姜東等［6］提出將面板與膠層等效為層合材料的蜂窩夾層復合材料模擬方法。針對蜂窩夾層復合材料不確定性已有相關研究［7－8］。寇東鵬等［7］通過對胞壁隨機移除的蜂窩結構動態變形過程進行有限元模擬，分析隨機缺陷對蜂窩結構變形模式影響。Flores等［8］用計算多尺度方法研究泡沫填充蜂窩芯結構力學行為的不確定性。而對蜂窩夾層材料不確定性的反問題尤其據動態性能識別材料不確定參數具有重要工程意義。。

有限元模型修正［9－12］可作為準確識別復合材料參數的有效方法。在不確定性描述［13］方法基礎上不確定性有限元模型修正得以發展。基于攝動法的模型修正，若待修正參數不確定程度較小則可高效獲得修正結果［14－15］。而基于區間分析的修正方法，待修正參數區間在迭代過程中易擴張，且每次迭代需用優化方法計算各參數區間，對實際結構計算量較大［16－17］。

本文采用基于攝動法的有限元模型修正理論識別蜂窩夾層復合材料不確定參數。提出蜂窩夾層復合材料不確定性參數識別方法，即①在蜂窩芯等效彈性參數理論分析基礎上用三明治夾心板理論建立鋁蜂窩夾層板初始有限元模型;②據芯層結構及相對靈敏度分析選待識別參數;③通過多組試驗數據獲得模態頻率均值與標準差，識別鋁蜂窩夾層板不確定性參數;④據識別后參數均值及標準差構造樣本，代入有限元模型中計算模態參數，并將計算與試驗結果統計特征進行比較，驗證方法的可行性。

1 蜂窩芯等效彈性參數

三明治夾心板理論通過蜂窩芯等效彈性參數模擬夾層板結構。認為上、下面板服從Kirchhoff假設，蜂窩芯層能抵抗橫向剪切變形且具有一定面內剛度，等效為均質、厚度不變的正交各向異性層。

蜂窩芯等效彈性參數可通過均勻化理論獲得［1，4－5］。蜂窩芯單胞見圖1。當l=h，θ=30°，即蜂窩芯胞元為正六邊形時，有

圖1 蜂窩芯單胞Fig.1 Unit cell of honeycomb core

式中:Ecx，Ecy，Ecz為等效彈性模量;Gcxy，Gcxz，Gcyz為等效剪切模量;Es為蜂窩芯材料彈性模量;Gs為蜂窩芯材料剪切模量;γ為修正系數，理論值取1，工程中一般取0.4～0.6;μxy=μyz=μxz=0.33為材料等效泊松比。

由質量等效可得蜂窩芯等效密度為

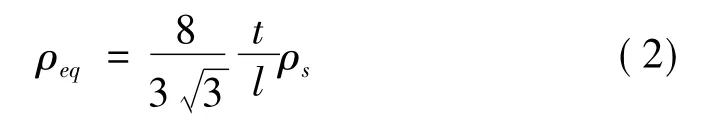
2 不確定性識別方法

用基于攝動法的不確定性有限元模型修正理論作為復合材料不確定彈性參數識別方法。確定性有限元模型修正可歸結為優化問題，即

式中:ε為模態參數殘差;zm，za(p)∈Rn分別為試驗與計算的模態參數;W為反映各模態參數殘差相對權重的對角陣。

在待識別材料參數p∈RN的合理取值范圍p1≤p≤p2內求解pA，使目標函數J( p)試驗與計算模態參數的加權殘差取極小值，則pA為參數的精確識別結果。待識別參數可通過相對靈敏度分析選取，避免參數量綱及數量級影響，即

式中:Sr為相對靈敏度矩陣;fi為第i階模態頻率;pj為第j個參數。

用靈敏度分析方法迭代求解式(3)，第j個迭代步的識別問題可描述為

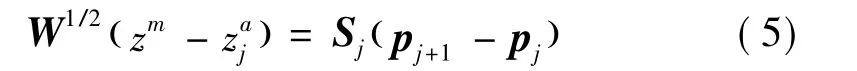
式中:Sj=W1/2?zj/?pj為模態參數對待識別參數的加權靈敏度矩陣。

考慮試驗模態參數及結構參數的不確定性，式(5)中參數應考慮為隨機參數，即

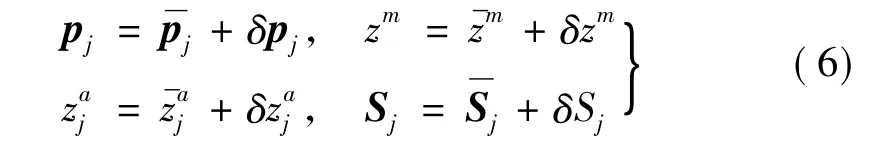
將式(6)代入式(5)可得不確定性結構參數識別問題的迭代方程為

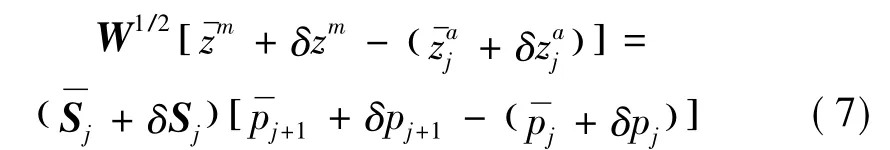
用攝動法將式(7)中關于δ的零階項及一階項分離，得

若計算模態參數對待識別參數的加權靈敏度矩陣病態，可用求解不適定問題的正則化方法求解式(8)。轉換矩陣變為

用式(14)計算待識別參數的協方差矩陣可避免計算模態參數對待識別參數的二階靈敏度矩陣從而減少計算量。由式(11)、(14)可求解不確定性結構參數識別問題。

3 算例研究

本文研究對象為鋁蜂窩夾層板，面板、芯層材料均為鋁合金，彈性模量68 GPa，密度2 700 kg/m3。試驗蜂窩夾層材料幾何參數見表1。通過對6塊同尺寸鋁蜂窩板自由－自由邊界條件的模態試驗，進行鋁蜂窩板彈性參數不確定性識別研究。

表1 試驗蜂窩夾層材料幾何參數(單位:mm)Tab.1 Geometrical parameters of honeycomb sandwich plate

3.1 模態試驗

試驗采用錘擊法，自由－自由邊界條件用橡皮繩將鋁蜂窩夾層板懸掛模擬，粗略計算模態振型布置加速度傳感器測點避開模態節點，確定試驗對象大致頻率范圍，設置采樣頻率。試驗頻率范圍0～1000 Hz，在蜂窩板面均勻布置121個激振點，激振方向垂直蜂窩板平面。對6塊鋁蜂窩夾層板試驗獲得6組模態振型及頻率。由于試驗或鋁蜂窩板不確定性，試驗結果存在一定離散性，前4階試驗模態頻率均值及標準差見表2。鋁蜂窩夾層板試驗模態振型見圖2。

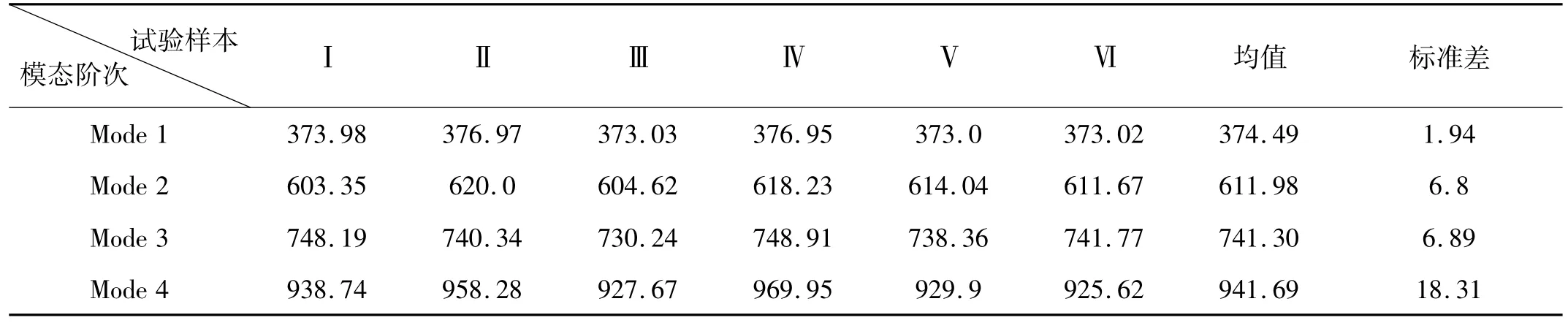
表2 鋁蜂窩夾層板試驗模態頻率Tab.2 Experimental modal frequencies of honeycomb sandwich plate

圖2 鋁蜂窩夾層板試驗模態振型Fig.2 Experimental mode shapes of honeycomb sandwich plate

3.2 不確定性參數識別

按蜂窩夾層復合材料不確定性參數識別步驟，據式(1)、(2)計算(γ取1)獲得蜂窩芯等效參數見表3。將表3參數作為初始值，面板與蜂窩芯分別采用殼單元及實體單元建立蜂窩夾層結構初始有限元模型。初始有限元模型計算、試驗模態頻率均值比較見表4，其中第一階模態頻率誤差最大為9.93%。

3.2.1待識別參數選取

通常選誤差部位或對結構動態特性敏感性較大參數。本文鋁蜂窩夾層板內部結構見圖3。因制造工藝等因素蜂窩芯胞元形狀及排列方式均不規則，導致鋁蜂窩芯層等效彈性參數存在一定不確定性;蜂窩夾層復合材料面板與芯層由膠層粘接，而膠層的力學性能遠弱于面板及芯層材料，導致面板與芯層間非理想剛性連接，弱層引起的層間剪切效應會造成鋁蜂窩夾層材料宏觀力學性能一定程度降低，可選面板參數為待識別參數［6］。

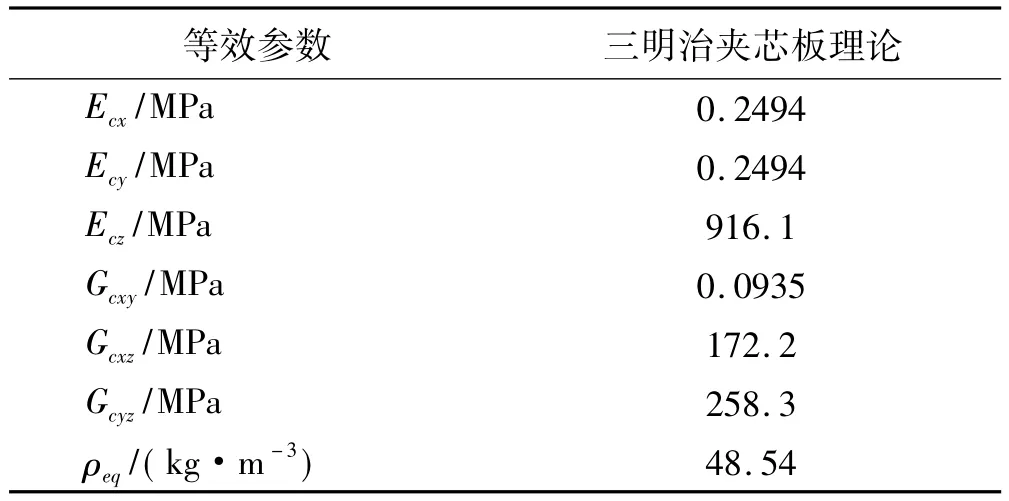
表3 蜂窩芯等效參數Tab.3 Equivalent elastic parameters of honeycomb core

表4 初始有限元模型計算、試驗模態頻率均值比較Tab.4 Comparison between the initial computational and experimental modal frequencies

在初始有限元模型基礎上分析鋁蜂窩板模態頻率對各參數靈敏度。便于比較，采用相對靈敏度。模態頻率對各參數的相對靈敏度見表5。由表5看出，各階頻率對面板厚度、蜂窩芯等效面外剪切模量Gcxz、Gcyz的相對靈敏度顯著高于其它等效彈性參數。

圖3 蜂窩夾層板內部結構Fig.3 Internal architecture of honeycomb sandwich plate

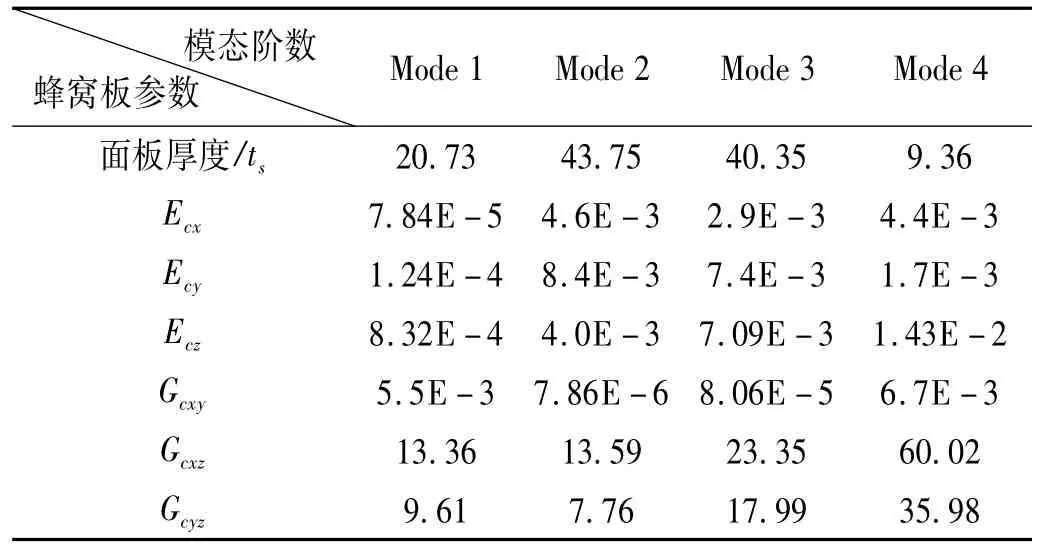
表5 鋁蜂窩夾層板各階頻率對各參數的相對靈敏度Tab.5 The relative sensitivity of frequencies with respect to parameters

3.2.2識別結果

選鋁蜂窩芯等效面外剪切模量Gcxz、Gcyz及面板厚度為待識別參數，用不確定性參數識別方法據6組試驗模態參數修正鋁蜂窩夾層板初始有限元模型，以獲得具有統計意義的結構參數。在參數識別迭代過程中取加權矩陣W=I，正則化參數λ=0，并對參數據可能的變化范圍施加約束求解。

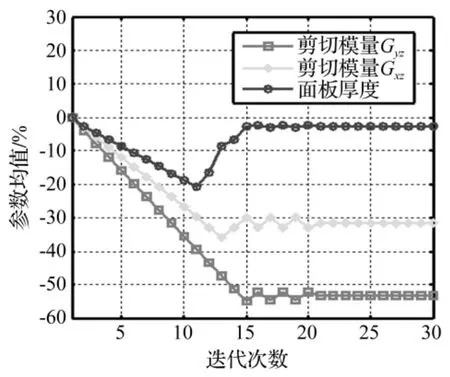
圖4 待識別參數均值收斂曲線Fig.4 Convergence of the mean－value of selected parameters

待識別參數均值收斂曲線見圖4，可見經20次迭代后參數均值收斂。識別前后不確定參數統計特性比較見表6。收斂后剪切模量Gyz均值變化量為－50%，Gxz均值變化量為－30%，將識別后結果代入等效剪切模量計算式(1)可反推出等效參數計算式中修正系數γ值。參數標準差初值取0，迭代收斂后識別出待識別參數標準差。計算模態參數均值誤差收斂曲線見圖5。據識別后結構參數均值及方差采用蒙特卡洛方法(Monte－Carlo Method)構造1000個樣本代入有限元模型中計算獲得1 000組模態參數，由此獲得計算模態參數的統計量。識別后計算結果與試驗模態參數統計量比較見表7。由表7看出，識別后前四階模態頻率均值最大誤差由初始模型的9.93%降到4.71%;模態參數標準差計算值接近試驗結果，能反映結構動態特性的離散性。該識別結果表明，對存在不確定性的鋁蜂窩夾層復合材料，用本文方法能準確識別鋁蜂窩夾層板不確定參數的統計特征包括參數均值及標準差，從而建立具有統計意義的準確動力學模型。

表6 識別前后不確定參數統計特性比較Tab.6 Comparison of statistical characteristics of selected parameters between before and after parameter identification

圖5 計算模態參數均值誤差收斂曲線Fig.5 Error convergence of the mean－value of computational modal data

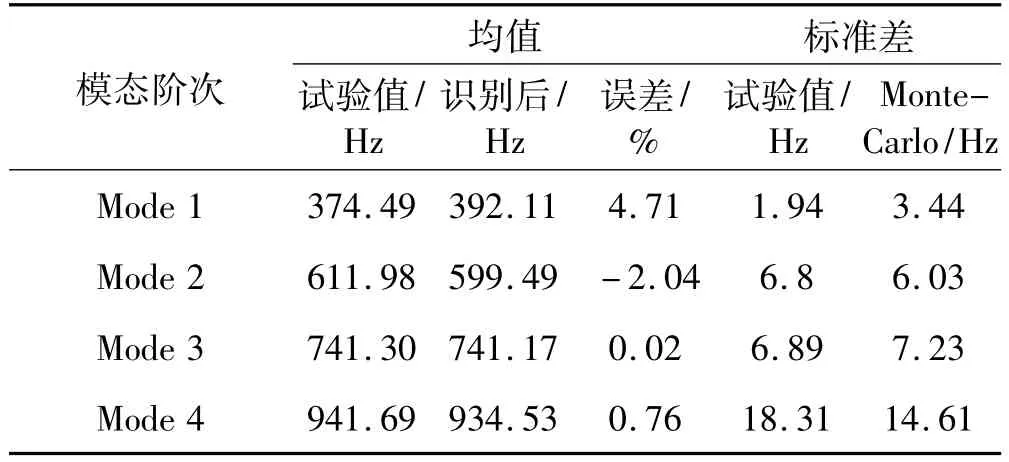
表7 識別后計算結果與試驗模態參數統計量比較(1000 samples)Tab.7 Comparison of statistical characteristic between identified computational results and experimental modal data

4 結論

本文通過所提蜂窩夾層復合材料不確定性參數識別方法，據蜂窩芯層等效彈性參數建立鋁蜂窩夾層板初始有限元模型，通過分析芯層結構及相對靈敏度選取待識別參數，并據6組試驗數據所得模態頻率均值及標準差識別鋁蜂窩夾層板不確定性參數。結論如下:

(1)對蜂窩夾層復合材料應選存在不確定性且對動態特性影響較大的參數進行識別。

(2)識別后鋁蜂窩板前四階模態頻率均值誤差絕對值最大不超過5%，模態參數標準差計算結果接近試驗值，可準確反映蜂窩板動態特性的離散性。

(3)該方法能準確識別鋁蜂窩夾層板不確定參數均值及標準差，可建立具有統計意義的準確動力學模型。

［1］Gibson L J，Ashby M F.Cellular solids structure and properties，secondedition［M］.CambridgeUniversity Press，1997.

［2］富明慧，尹久仁.蜂窩芯層的等效彈性參數［J］.力學學報，1999，31(1):113－118.

FU Ming－hui，YIN Jiu－ren.Equivalent elastic parameters of the honeycomb core［J］.Acta Mechanica Sinica，1999， 31(1):113－118.

［3］陳玳珩，楊璐.蜂窩復合材料的等價彈性模量［J］.力學學報，2011，43(3)，514－522.

CHEN Dai－heng，YANG Lu.Analysis of equivalent elastic modulus of a honeycomb sandwich［J］.Chinese Journal of Theoretical and Applied Mechani，2011，43(3):514－522.

［4］徐勝今，孔憲仁，王本利，等.正交異性蜂窩夾層板動、靜力學問題的等效分析方法［J］.復合材料學報，2000，17(3):92－95.

XU Sheng－jin，KONG Xian－ren，WANG Ben－li，et al. Method of equivalent analysis for statics and dynamics behavior of orthotropic honeycomb sandwich plates［J］.Acta Materiae Compositae Sinica，2000，17(3):92－95.

［5］張鐵亮，丁運亮，金海波.蜂窩夾層板結構等效模型比較分析［J］.應用力學學報，2011，28(3):275－282.

ZHANGTie－liang，DINGYun－liang，JINHai－bo. Comparative analysis of equivalent models for honeycomb sandwich plates［J］.Chinese Journal of Applied Mechanics，2011，28(3):275－282.

［6］寇東鵬，虞吉林，鄭志軍.隨機缺陷對蜂窩結構動態行為影響的有限元分析［J］.力學學報，2009，41(6):859－868.

KOU Dong－peng，YU Ji－lin，ZHENG Zhi－jun.Effect of randomly removing cell walls onthedynamiccrushing behavior of honeycomb structures［J］.Acta Mechanica Sinica，2009，41(6):859－868.

［7］姜東，江智遠，費慶國，等.考慮膠層的蜂窩夾層復合材料動態特性［J］.東南大學學報(自然科學版)，2013，43(5):1068－1073.

JIANG Dong，JIANGZhi－yuan，FEIQing－guo，etal. Dynamic characteristics of honeycomb sandwich composite considering effect of adhesive layer［J］.Journal of Southeast University(Natural Science Edition)，2013，43(5):1068－1073.

［8］Flores E S，DiazDelaO F，Friswell M，et al.A computational multi－scale approach for the stochastic mechanical response of foam－filled honeycomb cores［J］.Composite Structures，2012(94):1861－1870.

［9］Mottershead J E，Link M，Friswell M I.The sensitivity method in finite element model updating:a tutorial［J］. Mechanical Systems and Signal Processing，2011，25:2275－2296.

［10］費慶國，張令彌，李愛群，等.基于統計分析技術的有限元模型修正研究［J］.振動與沖擊，2005，24(3):23－26.

FEI Qing－guo，ZHANG Ling－mi，LI Ai－qun，et al.Finite element model updating using statistics analysis［J］.Journal of Vibration and Shock，2005，24(3):23－26.

［11］費慶國，張令彌，郭勤濤.GARTEUR有限元模型修正與確認研究［J］.航空學報，2004，25(4):372－375.

FEI Qing－guo，ZHANG Ling－mi，GUO Qin－tao.Case study of FE model updating and validation via an aircraft model structure［J］.Acta Aeronautica et Astronautica Sinica，2004，25(4):372－375.

［12］郭勤濤，張令彌，費慶國.結構動力學有限元模型修正的發展—模型確認［J］.力學進展，2006，36:36－42.

GUO Qin－tao，ZHANG Ling－mi，FEI Qing－guo.From FE model updating to model validation:advances in modeling ofdynamic structures［J］.Advances in Mechanics，2006，36: 36－42.

［13］Moens D，Vandepitte D.A survey of non－probabilistic uncertaintytreatmentinfiniteelementanalysis［J］. Computer Methods in Applied Mechanics and Engineering. 2005，194:1527－1555.

［14］KhodaparastHH，MottersheadJE，FriswellMI. Perturbationmethodsfortheestimationofparameter variability in stochastic model updating［J］.Mechanical Systems and Signal Processing，2008，22:1751－1773.

［15］Hua X G，Ni Y Q，Chen Z Q，et al.An improved perturbation methodforstochasticfiniteelementmodel updating［J］.International Journal for Numerical Methods in Engineering，2008，73:1845－1864.

［16］Khodaparast H H，Mottershead J E，Badcock K J.Interval model updating with irreducible uncertainty using the Kriging predictor［J］.Mechanical Systems and Signal Processing，2011，25:1204－1226.

［17］王登剛，秦仙蓉.結構計算模型修正的區間反演方法［J］.振動工程學報，2004，17(2):205－209.

WANG Deng－gang，QIN Xian－rong.Interval method for computational model updating of dynamic structures［J］. Journal of Vibration Engineering，2004，17(2):205－209.

［18］Ahmadian H，Mottershead J E，Friswell M I.Regularization methods for finite element model updating［J］.Mechanical Systems and Signal Processing，1998，12: 47－64.

Parameter identification approach of honeycomb sandwich composite with uncertainties

JIANG Dong1，2，WU Shao－qing1，2，FEI Qing－guo1，2，HAN Xiao－lin1，2
(1.Department of Engineering Mechanics，Southeast University，Nanjing 210096，China; 2.Jiangsu Key Laboratory of Engineering Mechanics，Nanjing 210096，China)

An approach of parameter identification for predicting uncertainties in honeycomb sandwich composite is provided.The initial finite element model of a honeycomb plate is constructed by the application of an appropriate sandwich theory，in which the equivalent parameters were predicted by homogenization method.According to the analysis of the internal honeycomb structure and the relative sensitivity of eigenvalues with respect to system parameters，the sensitive parameters including the uncertainties(Gcxz，Gcyzand thickness of the face sheet)are selected to be identified. Through modal experiments of six different honeycomb plates with free－free boundary condition，the mean values and deviations of the modal frequencies are obtained，using which the uncertain parameter identification of honeycomb sandwich plate is conducted.Identification results show that when considering the uncertainty in honeycomb sandwich composite，the proposed identification method can be used for accurately identifying the mean values and deviations of the uncertain parameters and the dynamical finite element model with statistical significance can be constructed.

honeycomb sandwich composite;uncertainty;finite element method;parameter identification;witn satisfactory

V250.3;TB303

A

10.13465/j.cnki.jvs.2015.02.003

教育部新世紀優秀人才支持計劃(NCET－11－0086);江蘇高校優勢學科建設工程資助項目(1105007001)

2013－10－09修改稿收到日期:2014－01－15

姜東男，博士生，1985年生

費慶國男，博士，教授，博士生導師，1977年生郵箱:qgFei@seu.edu.cn